加权无标度网络病毒传播和局部免疫策略研究①
2017-07-19刘瑞军
刘瑞军
(武夷学院 实验室管理中心, 武夷山 354300)
加权无标度网络病毒传播和局部免疫策略研究①
刘瑞军
(武夷学院 实验室管理中心, 武夷山 354300)
为了进一步描述现实生活中复杂网络的病毒传播问题, 改进加权无标度网络模型的传统构造方法, 考虑流量带宽和个体抵抗力两个重要因子, 利用平均场理论模拟仿真病毒传播过程, 对实验数据进行分析, 验证该模型的有效性. 现实生活中往往只能了解复杂网络的局部拓扑信息,传统病毒免疫策略大多基于全局拓扑信息, 在仅了解局部信息的前提下, 提出加权无标度网络中基于局部最优的病毒免疫策略, 通过动态模拟病毒传播的免疫仿真实验, 与随机免疫策略和目标免疫策略对病毒传播影响进行比较, 验证局部最优免疫策略的有效性.
加权无标度网络; 病毒传播; 流量带宽; 个体抵抗力; 局部最优
1 引言
近年来, 随着互联网的日益普及, 改善了人们的生活环境, 同时也为计算机病毒的生存和发展提供了有利条件. 在社会高速发展过程中, 人类曾多次遭遇毁灭性的计算机病毒攻击, 造成严重的经济损失. 同时, 计算机病毒安全问题甚至关系到一个国家的安定稳定,一种微不足道的新型病毒很可能使整个国家甚至大半个世界的网络陷入瘫痪, 不但给生活带来不便, 甚至给国防带来危机. 为了让人类生活在安全的互联网环境中, 从计算机病毒第一次出现后, 许多科学家就开始模拟病毒传播, 希望能预测计算机病毒的传播过程并有效的遏制病毒的泛滥.
1999年Faloutsos等人[1]发现, 互联网表现出很强的幂律分布特点, 节点的度有很大的波动性[1,2]. 目前为止主要从两种不同的角度来描绘互联网的结构[1,3]. 尽管随着时间的推移, 系统中的节点和边在不断增加, 但网络拓扑结构特性却不会发生很大的变化[4]. 大量研究表明网络上的病毒传播与网络的拓扑结构有着密切的联系[5-8], 在BA无标度网络中, 当节点数近似无穷时, 病毒的有效传播率阈值近似于0. 1998年, Steve White提出了五个关于计算机病毒研究问题[9], 其中最具争议性的问题是理论上的计算机病毒传播速率远超于现实. 现实中感染30万台主机需24小时左右[10], 然后理论上计算机病毒感染100万台主机所需时间还不到1秒[11].
针对互联网上病毒传播速度现实与理论的巨大差异以及现实互联网络的增长模式, 本文建立了引入边权值表示流量带宽节点值表示个体抵抗力的改进加权无标度网络模型. 根据模型, 分别观察了初始感染节点的选择、个体抵抗力差异、流量带宽限制等对病毒传播的影响. 以往的病毒免疫策略[12]研究, 大多基于对网络全局拓扑信息而做出的, 现实生活中, 大部分复杂网络[13]仅仅局限于了解其局部拓扑信息. 针对现实情况,本文提出了加权无标度网络中基于局部最优信息的病毒免疫策略, 通过与随机免疫策略和目标免疫策略的比较, 观察其是否有效.
2 模型及理论分析
2.1 加权无标度网络模型
传统加权无标度网络模型中, 边权值wi,j通常表示节点i, j间的熟悉程度,, 病毒的有效传播率正 比于越大, 表示i, j节点之间越熟悉, 相似度越大, 当其中一个节点感染病毒时, 另一个节点感染病毒的概率也越大; 反之, 表示i, j节点之间越陌生, 相似度越小, 当其中一个节点感染病毒时, 另一个节点感染病毒的概率也越小.
模型的构造算法[5]如下:
Step1. 增长: 从一个具有m0个节点的网络开始, m0个节点相互连接, 每次引入一个新的节点i, 并且分别连到m个已存在的节点上, 假设与节点j相连, 则i, j之间的边权值为, 这里
Step2. 优先连接: 一个新的节点与一个已经存在的节点i相连接的概率与节点i的度, 节点j的度之间满足公式(1)关系:

经过理论和实验证明, 无标度网络的度分布满足幂律关系, 度分布函数[5], 其中k为节点的度,r通常取2~3[14]之间的值.
2.2 改进后的加权无标度网络模型
问题1. 计算机病毒在互联网上的传播速率远低于理论值, 现实考虑病毒传播速率缓慢的原因为病毒高峰期时由于传输路径本身容量的限制而发生拥塞现象和个体本身的不同防护措施使其不容易被病毒感染,某些节点如果度相对较大, 说明比较重要, 它就会相对与其他节点具有更强的病毒抵御能力, 而且通过它的传输路径容量也相对较大. 为此引入了流量带宽和个体抵抗力因子. 其中, 用节点本身的权值vi表示每个不同个体之间拥有的不同抵抗力, vi越大, 个体抵抗力越强, 被病毒感染的几率越低; 用节点之间的边权值wi,j表示节点i, j之间的流量带宽,越大, 表示该条路径的容量越大, 发生拥塞的可能性越低, 病毒在该条路径上传播得越顺畅, 个体抵抗力在这条路径上发挥的作用相对就比较微弱. 反之, 病毒在该路径上的传播速度将受到相应的抑制.
问题2. 传统加权无标度网络模型构造方法存在以下弊端: Step1中网络每增加一个节点, 均产生m条边,节点和边的增长都很规律, 但现实互联网节点与边的增长并不是特别规律.
根据问题1和问题2, 本文对传统加权无标度网络模型的构造方法进行改进, 具体构造算法如下:
Step1. 增长: 从一个只有1个节点的网络开始, 该节点拥有抵抗力值v1, 每次引入一个新的节点j, 并且按概率pi分别与所有存在的节点相连, 假设与节点i相连, 则i, j之间的边权值为wi,j, 抵抗力vi的值更新为v’i, 如公式(2):
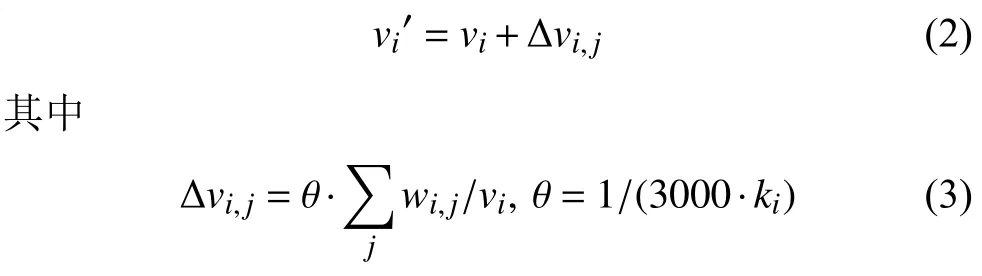
θ是增量因子, 根据节点i当前度的大小ki进行调节.表示节点i的当前总带宽流量wi, 由公式(3)可知抵抗力增量与节点自身抵抗力呈负相关, 与节点带宽总流量呈正相关, 重要的节点抵抗力增加的速度高于一般节点, 特别是相对重要的节点本身抵抗力较弱时, 人们就会对其重点保护, 大幅度提高其抵抗能力, 这与现实中的问题1相符.
Step2. 优先连接: 一个新的节点与一个已经存在的节点i相连接的概率pi与节点i的边权和wi, 节点j的边权和wj之间的关系如公式(4):
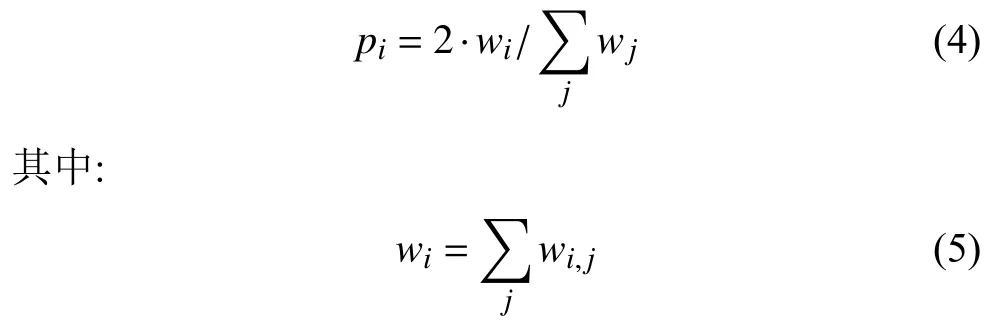
新增的节点偏向与网络中的重要节点相连, 但也存在与微弱节点相连的可能.
Step3. 若新增加的节点经过Step1和Step2后仍是个孤立点, 则使其与网络中相对序号最小的度最大节点相连.
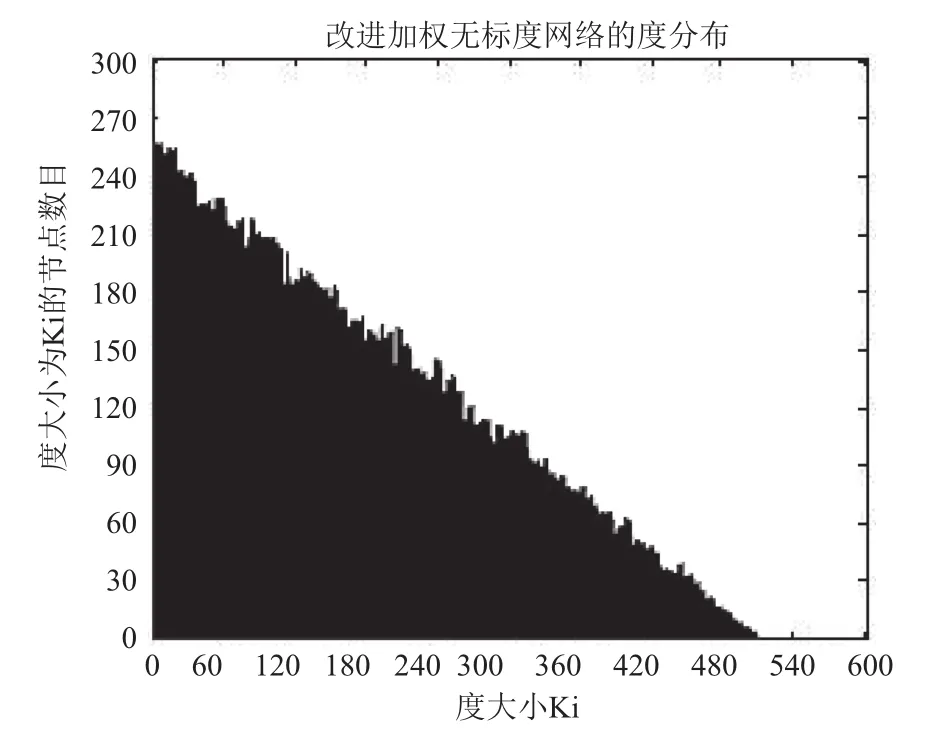
按上述算法构造出节点数目为5000个的改进后加权无标度网络模型(具体参数设置请参见第五章节实验结果与分析), 其度分布如图2, 排除干扰点, 取其中的七组坐标数据进行计算, 坐标数据如表1, 计算结果的r值约为0.73, 即, 虽然与经典的r值在2~3之间有一定差距, 但由度分布图可知改进的构造方式符合无标度网络选择增长和优先连接的特性, 具有现实网络可参照性.
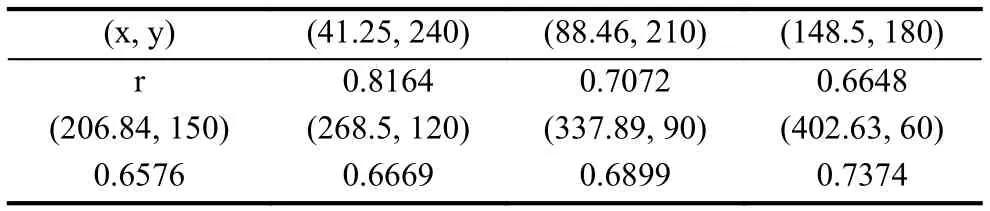
表1 度分布测试数据
3 动态模拟病毒传播过程
通过研究无标度网络上的SIS[15]和SIR[16]病毒传播过程, 本文结合当前建立的改进后加权无标度网络模型, 分析病毒在该模型上的SIS(R)传播过程, 过程如图1所示.
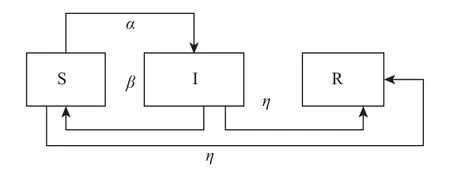
图1 SIS(R)传播模型
个体被划分为三种不同的类型: 易感种群类(S), 他们不会感染其他个体, 但有可能被其他感染个体感染;感染种群类(I), 他们已经被感染, 而且会感染易感个体,具有传染性; 免疫种群类(R), 他们是经过人为免疫策略而使其达到免疫状态, 不会感染其他个体, 也不会被其他个体感染. 在图2中, 若易感节点与感染节点接触,它就有α概率的可能变成感状节点; 感染节点本身有β概率的可能恢复到易感节点状态. 无论是易感还是感染节点, 经过人为干预, 都有π概率的可能变成免疫节点. 研究中, 我们定义:
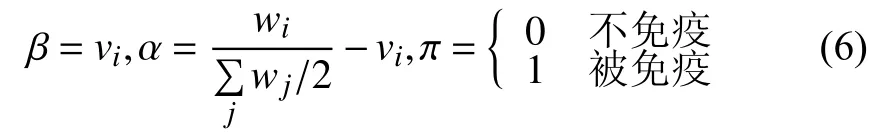
自我恢复率β与个体抵抗力vi相关, 如果被感染节点的个体抵抗力越强, 其恢复成易感节点的概率越高;被感染率α与该节点的边权总和以及个体抵抗力相关,如果易感节点边权和很大, 且其抵抗力相对较弱, 则其极易受感染; 免疫率非0即1, 如果对某点采取免疫措施,则其变为免疫状态, 如果未采取任何免疫策略, 则其为原易感或感染状态. 若不存在人为的免疫策略, 则SIS(R)模型退化为SIS模型.
利用平均场理论, 假设网络中度值为k的节点中易感个体比例为, 感染个体比例为ρk(t), 免疫个体比例为, 其中Sk(t)+ρk(t)+Rk(t)=1, k=1, 2, ……, n. 建立公式(7)病毒传播动力学方程如下:
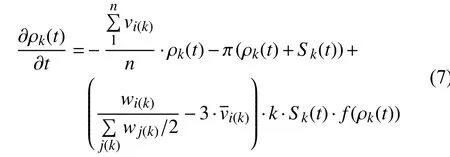
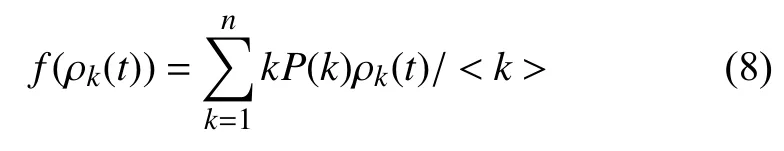
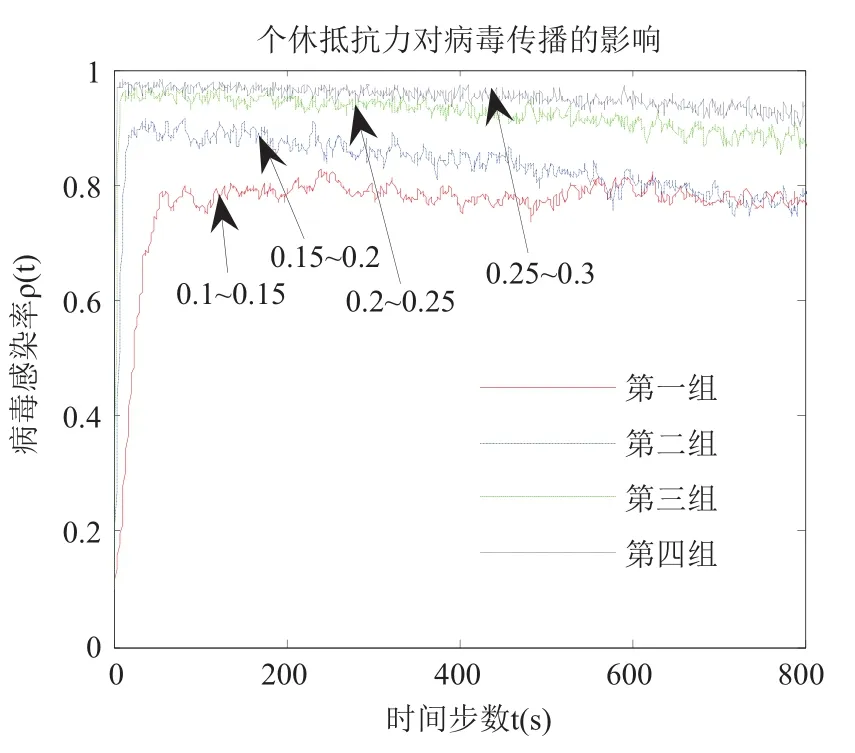
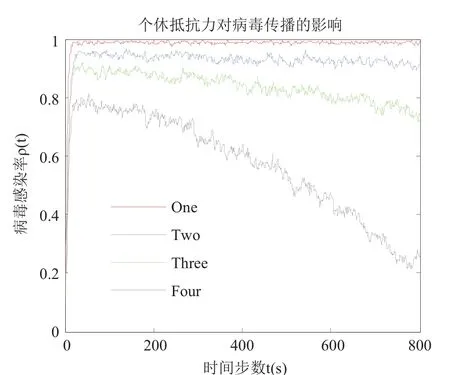
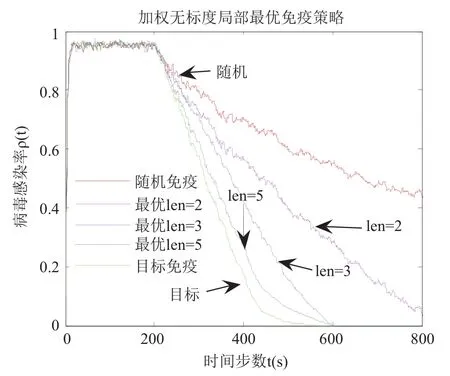
其中, n为节点的最大度值, P(k)表示度值为k的节点占所有节点的比例; 通过理论推导的公式(13)可知, 在无免疫策略前提下, 加权无标度网络的病毒传播的最终感染率与个体抵抗能力、度分布和边权带宽值之间密切相关. 4.1 传统病毒控制策略 抑制病毒传播的一种重要方法是人为干预, 引入免疫策略. 目前, 主要的免疫方法有随机免疫策略、目标免疫策略和熟人免疫策略[17]. 本文仅讨论随机免疫和目标免疫策略. 随机免疫策略通过随机的方式选取若干个节点进行免疫, 不考虑节点中的个体差异, 每个节点被选到的概率都相等, 实验表明, 随机免疫虽然能局部抑制病毒的传播, 但对于要彻底消灭病毒, 需对网络中的绝大多数节点进行免疫, 这显然不现实. 目标免疫策略优先选取网络中重要的节点进行免疫, 考虑节点间的差异, 越重要但本身越脆弱的节点首先被考虑进行免疫, 实验表明, 仅对少量节点进行免疫就可以达到彻底消灭病毒的目的. 4.2 基于局部最优病毒控制策略 传统的随机免疫和目标免疫均为基于网络全局拓扑信息的免疫策略, 然后现实生活中对一个网络全局信息的掌握十分有限, 特别是对一些庞大的复杂网络.传统的免疫实验大多预先对需要免疫的节点进行免疫,然后再观察病毒的传播现象, 与现实生活中的实时免疫相悖. 因此, 针对上述问题, 本文提出了基于局部最优信息的动态免疫策略. 出于现实考虑, 假设(1): 每次动态地选择N个点进行免疫, 而不是一次性把该免疫的节点全部免疫了. 假设(2): 由于发现病毒的滞后性, 当采取免疫措施时病毒已达到感染峰值. 假设(3): 由于不能全局性的发现病毒存在, 实验中每个阶段仅知道部分节点感染病毒, 即病毒获知率S为0~1之间的数值.该免疫策略关键步骤如下: Step1. 对所获知的被感染节点i, 计算与i相距len(直接相连距离为1)距离以内所有临近节点各自的容量和wx, x表示网路中以i节点为中心, 以len为半径的所有节点集, 表示与i节点临近的节点集各自的容量和. Step2. 对wx中所有节点的容量和进行从大到小排序, 选择前N个节点进行免疫. 若n(Wx) Step3. 若n(Wx)=0, 结束计算, 否则转Step1. 仿真实验过程, 改进后加权无标度网络的节点规模为5000个, 通常情况下足以体现现实复杂网络模型的主要病毒传播特征. 个体抵抗力vi取0.01~0.05之间的数值, 节点间的流量带宽取0.1~0.3之间的数值,基于局部最优免疫策略算法过程中感染病毒节点的获知率S设置为0.1~0.5之间以及距离len值取1~5之间的整数, 初始感染率统一取值为0.1, 即随机选取网络中十分之一的节点为被感染节点, 其他均为易感节点.按改进后的加权无标度网络构造算法构造出网络模型的度分布如图2所示, 具体数据分析见表1. 图2 改进后加权无标度模型的度分布 5.1 流量带宽大小对病毒传播的影响 现实的病毒传播速度与理论存在巨大差异, 为验证所述流量带宽是否为影响病毒传播的因素之一, 本文对在仅流量带宽变化的情况下对病毒传播行为进行仿真实验. 仿真中, vi取0.02~0.03之间数值,分别取表2中的四组测试数据. 表2 流量带宽测试数据 四组数据的流量带宽逐渐增加, 仿真结果如图3所示. 由图3可知, 无标度网络中随着整体流量带宽大小的增大, 病毒传播速度和最终病毒感染率都随之增加.当流量带宽均值在0.2以上时, 病毒传播行为基本不受太大影响, 只是在小范围内波动. 由此得知, 流量在一定阈值范围内可以抑制病毒传播行为, 同时也验证了实际生活中病毒大量爆发时由于带宽的限制而相互制约, 从而导致传播速度小于理论值. 5.2 个体抵抗力强弱对病毒传播的影响 每个个体对同一种病毒的抵抗力不尽相同, 当一个个体的抵抗力强度较大时, 不仅能较快地从感染状态恢复到易感状态, 而且能在一定程度上遏制病毒对自身的感染. 为了进一步了解加权无标度网络上个体抵抗力强弱对病毒传播的影响, 仿真中取0.1~0.2之间数值, vi分别取值0.01~0.02、0.02~0.03、0.03~0.04和0.04~0.05四组数据进行测试, 仿真结果如图4所示. 图3 流量带宽大小差异 图4 个体抵抗力强弱差异 从图4可以看出, 加权无标度网络中, 节点抵抗力强弱差异对病毒传播速度的影响较小, 对病毒峰值的影响较大, 当初始个体抵抗力强度达到0.05左右时, 由于抵抗力随时间不断增大, 最终将影响最终的病毒感染比例. 个体抵抗力强弱将最终印象病毒的感染比例. 5.3 基于局部最优免疫策略对病毒传播的影响 为了验证加权无标度网络上基于局部最优病毒传播免疫策略的有效性, 对病毒传播采取了免疫措施. 仿真中取0.1~0.2之间数值, vi取0.02~0.04之间数值,S =0.15且len分别取2, 3, 5, 观察len在不同取值时对局部最优免疫效果的影响, 并与随机免疫、目标免疫进行了比较, 效果如图5所示. 图5 加权无标度局部最优免疫效果 由图5可以看出局部最优免疫策略相对于目标免疫策略和随机免疫策略来说都是一种有效的免疫方法,虽然局部最优免疫策略的效果不如目标免疫策略, 但随着len的增大, 局部最优免疫策略的效果将接近目标免疫, 当len取值为5时, 最优免疫策略的效果已经非常接近目标免疫了. 现实世界中, 很难了解网络的全局信息, 所以局部最优免疫策略具有现实意义. 计算机病毒的日益泛滥严重威胁着网络安全, 了解病毒在复杂网络上的传播行为及其性质对我们采取免疫措施至关重要. 不同的网络采取的免疫措施不同,同一种网络采取不同的免疫措施效果也不同. 经过仿真研究, 验证了加权无标度中基于最优免疫策略对病毒传播抑制的有效性, 特别是在仅仅了解局部信息的前提下, 大大提高了性价比. 在现实工作中, 我们可结合局部最优免疫策略对病毒采取免疫措施, 从而提高网络系统的可靠和安全性. 本文的研究中, 仅考虑只有一种病毒存在的传播模型及免疫策略, 然而现实生活中计算机往往同时存在多种病毒. 不同病毒之间在复杂网络上的相互竞争与合作关系值得我们进一步深究. 1Faloutsos M, Faloutsos P, Faloutsos C. On power-law relationships of the Internet topology. ACM SIGCOMM Computer Communication Review, 1999, 29(4): 251–262.[doi: 10.1145/316194] 2Vazquez A, Pastor-Satorras R, Vespignani A. Large-scale topological and dynamical properties of Internet. http://arxiv.org/abs/cond-mat/0112400. 3Chen GR, Fan ZP, Li X. Modelling the complex Internet topology. Complex Dynamics in Communication Networks.Berlin, Springer-Verlag. 2005. 213–234. 4李涛, 关治洪, 吴正平. 病毒在无标度网络上的传播及控制仿真研究. 计算机应用研究, 2007, 24(12): 177–178. [doi:10.3969/j.issn.1001-3695.2007.12.056] 5汪小帆, 李翔, 陈关荣. 复杂网络理论及其应用. 北京: 清华大学出版社, 2006. 6WANG CX, Knight JC, Elder MC. On computer viral infection and the effect of immunization. IEEE 16th Annual Conference Computer Security Applications. New Orleans,USA. 2000. 246–256. 7Vázquez A, Pastor-Satorras R, Vespignani A. Large-scale topological and dynamical properties of the Internet. Physical Review E, 2002, (65): 066130. [doi: 10.1103/PhysRevE.65.066130] 8Li X, Chen GR, Li CG. Stability and bifurcation of disease spreading in complex networks. International Journal of Systems Science, 2004, 35(9): 527–536. [doi: 10.1080/00207720412331285869] 9White SR. Open problems in computer virus research. Proc.of Virus Bulletin Conference. Munich, Germany. 1998. 10Moore D. The spread of the code-red worm. http://www.caida.org/research/security/code-red/coderedv2_analysis.xml. 11Staniford S, Moore D, Paxson V, et al. The top speed of flash worms. Proc. of the 2004 ACM workshop on Rapid malcode.Washington DC, USA. 2004. 33–42. 12朱刚, 张宁, 马良. 复杂网络上计算机病毒传播和控制策略研究. 计算机应用研究, 2006, 23(9): 54–56. 13黄金源, 张宁, 肖仰华. 基于拷贝模型的复杂网络鲁棒性研究. 计算机应用研究, 2010, 27(4): 1403–1406. 14Dorogovtsev SN, Mendes JFF, Samukhin AN. Structure of growing networks with preferential linking. Physical Review Letters, 2000, 85(21): 4633–4636. [doi: 10.1103/PhysRevLett.85.4633] 15Pastor-Satorras R, Vespignani A. Epidemic spreading in scale-free networks. Physical Review Letters, 2001, 86(14):3200–3203. [doi: 10.1103/PhysRevLett.86.3200] 16Zhou T, Fu ZQ, Wang BH. Epidemic dynamics on complex networks. preprint physics/0508096, 2005. 17Cohen R, Havlin S. Scale-free networks are ultrasmall.Physical Review Letters, 2003, 90(5): 058701. [doi: 10.1103/PhysRevLett.90.058701] Research on the Local Immunization Strategy of Virus Spreading in Weighted Scale-Free Networks LIU Rui-Jun In order to further describe the virus propagation of real-life complex networks, this paper improves the traditional construction methods of weighted scale-free networks model which considers two key factors: flow bandwidth and individual resistance. Using mean-field theory to simulate the process of the virus transmission, this article analyses the experimental data and verifies the validity of the new model. Most real-life complex networks are known to us with only the local topology information and the traditional virus immunization strategies are based on global network topology information. In condition of knowing local topology information, this paper proposes the immunization strategy of virus spreading based on the local optimum in weighted scale-free networks. Compared with the random immunization strategy and target immunization strategy about the efficiency of virus spreading in weighted scale-free networks, the local optimum immunization strategy is verified to be valid through the dynamic simulation of virus propagation. weighted scale-free networks; virus spreading; flow bandwidth; individual resistance; local optimum 刘瑞军.加权无标度网络病毒传播和局部免疫策略研究.计算机系统应用,2017,26(7):263–268. http://www.c-s-a.org.cn/1003-3254/5835.html 福建省教育厅基金(JK2012056) 2016-10-13; 收到修改稿时间: 2016-11-28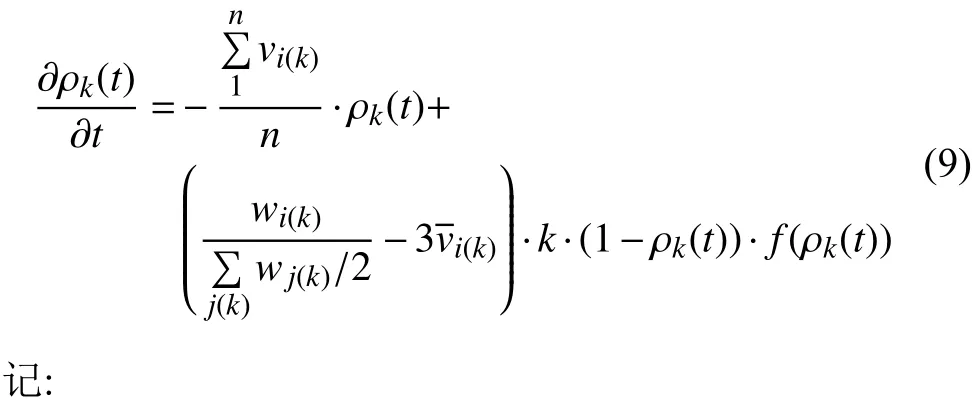
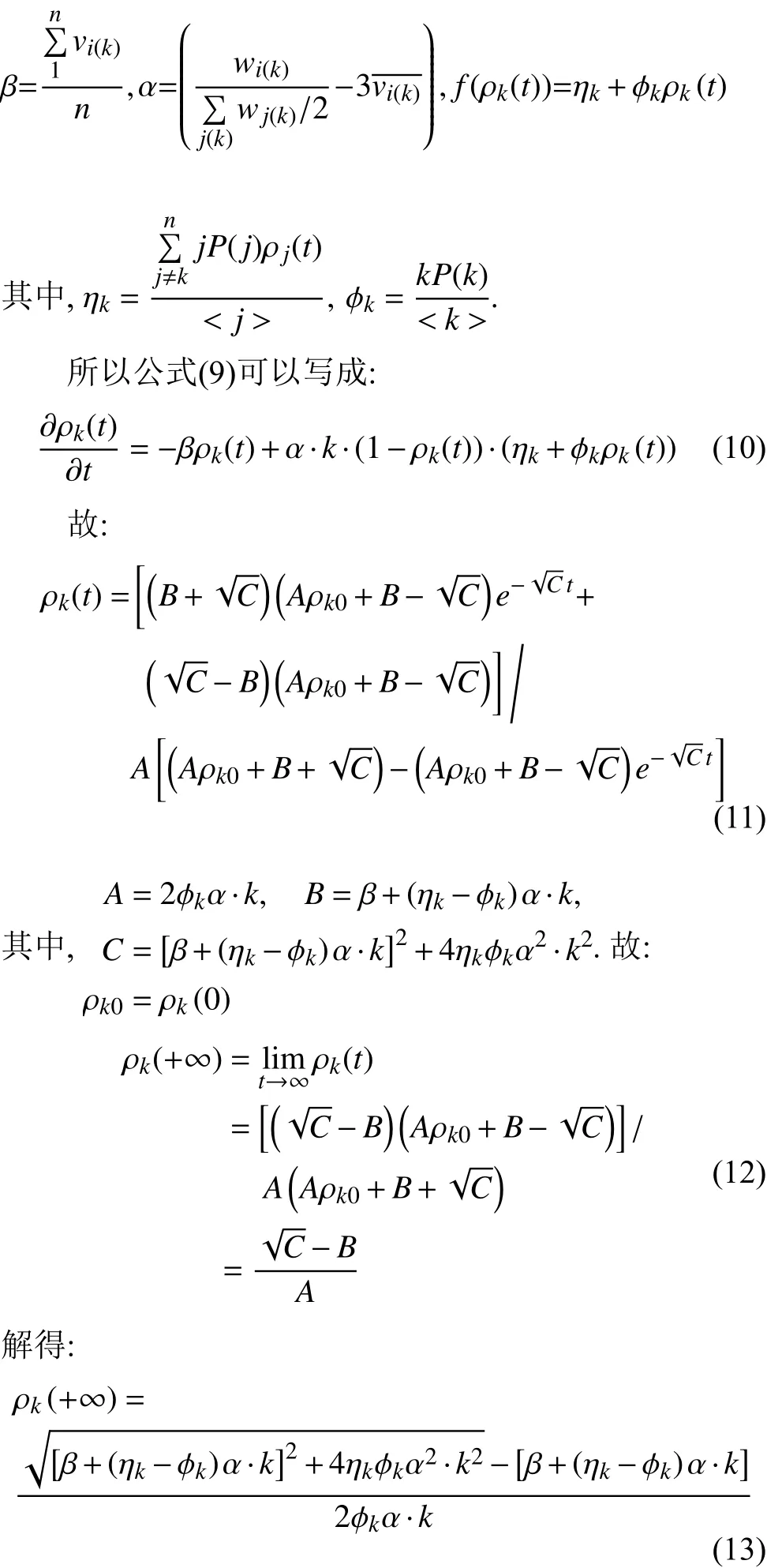
4 病毒控制策略
5 实验结果与分析
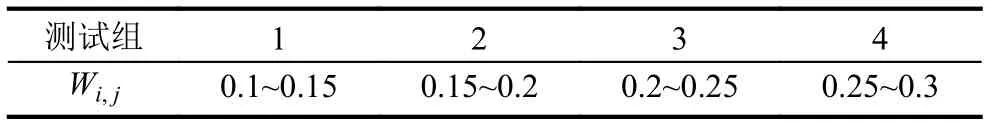
6 结束语
(Laboratory Management Center, Wuyi University, Wuyishan 354300, China)
