THE GROWTH ON ENTIRE SOLUTIONS OF FERMAT TYPE Q-DIFFERENCE DIFFERENTIAL EQUATIONS

LIU Xin-ling,LIU Kai

(Department of Mathematics,Nanchang University,Nanchang 330031,China)

THE GROWTH ON ENTIRE SOLUTIONS OF FERMAT TYPE Q-DIFFERENCE DIFFERENTIAL EQUATIONS

LIU Xin-ling,LIU Kai

(Department of Mathematics,Nanchang University,Nanchang 330031,China)

This paper is devoted to consider the entire solutions on Fermat typeq-di ff erence di ff erential equations.Using the classical and di ff erence Nevanlinna theory and functional equations theory,we obtain some results on the growth of the Fermat typeq-di ff erence di ff erential equations.

q-di ff erence di ff erential equations;entire solutions; fi nite order

1 Introduction

Letf(z)be a meromorphic function in the complex plane.We assume that the reader is familiar with standard symbols and fundamental results of Nevanlinna theory[5,16].As we all know that Nevanlinna theory was extensively applied to considering the growth,value distribution,and solvability of meromorphic solutions of di ff erential equations[6].Recently,di ff erence analogues of Nevanlinna theory were established,which also be used to consider the corresponding properties of meromorphic solutions on di ff erence equations orq-di ff erence equations,such as[2,4,7-12,14,17].

Let us recall the classical Fermat type equation

Equation(1.1)has the entire solutionsf(z)=sin(h(z))andg(z)=cos(h(z)),whereh(z)is any entire function,no other solutions exist.However,the above result fails to give more precise informations wheng(z)has a special relationship withf(z).Yang and Li[15] fi rst considered the entire solutions of the Fermat type di ff erential equation

and they proved the following result.

Theorem A[15,Theorem 1]The transcendental meromorphic solutions of(1.2)must satisfy

Tang and Liao[13]further investigated the entire solutions of a generalization of(1.2)as follows

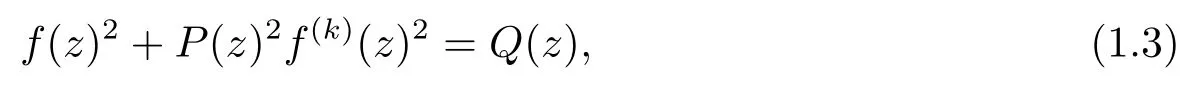
whereP(z),Q(z)are non-zero polynomials and obtained the next result.

Theorem B[13,Theorem 1]If the di ff erential equation(1.3)has a transcendental meromorphic solutionf,thenP(z)≡A,Q(z)≡B,kis an odd andf(z)=bsin(az+d),wherea,b,dare constants such thatAak=±1,b2=B.

Recently,the di ff erence analogues of Nevanlinna theory were used to consider the solutions properties of Fermat type di ff erence equations.Liu,Cao and Cao[8]investigated the fi nite order entire solutions of the di ff erence equation,wherePis non-zero constant and

here and in the following,cis a non-zero constant andP(z),Q(z)are non-zero polynomial,unless otherwise speci fi ed.The result can be stated as follows.

Theorem C[8,Theorem 1.1]The transcendental entire solutions with fi nite order of(1.4)must satisfyf(z)=sin(Az+B),whereBis a constant and,kis an integer.

Furthermore,Liu and Yang[10]considered a generalization of(1.4)as follows

and obtained the following result.

Theorem DLetP(z),Q(z)be non-zero polynomials.If the di ff erence equation(1.5)admits a transcendental entire solution of fi nite order,thenP(z)≡±1 andQ(z)reduces to a constantq.

If an equation includes theq-di ff erencef(qz)and the derivatives off(z)orf(z+c),then this equation can be calledq-di ff erence di ff erential equation.Liu and Cao[11]considered the entire solutions on Fermat typeq-di ff erence di ff erential equation

and obtained the following result.

Theorem E[11,Theorem 3.1]The transcendental entire solutions with fi nite order of(1.6)must satisfyf(z)=sin(z+B)whenq=1,andf(z)=sin(z+kπ)orf(z)=-sin(z+kπ+)whenq=-1.There are no transcendental entire solutions with fi nite order when1.

By comparing with the above fi ve theorems,we state the following questions which will be considered in this paper.

Question 1From Theorem A to Theorem E,we remark that the order of all transcendental entire solutions with fi nite order of di ff erent equations are equal to one.Hence,considering a generalization of equation(1.6),such as

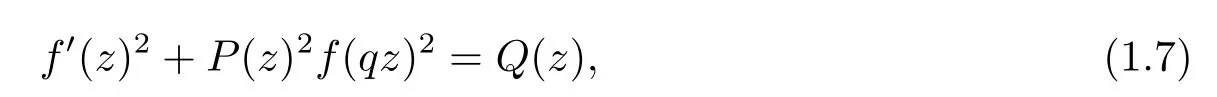
it is natural to ask if the fi nite order of the entire solutions of(1.7)is equal to one or not?

Question 2From Theorem B to Theorem E,the existence of fi nite order entire solutions of(1.3)and(1.5)forces the polynomialP(z)reduce to a constant.Is it also remain valid for equation(1.7)?

However,Examples 1 and 2 below show that Questions 1 and 2 are false in generally.

Example 1Entire functionf(z)=sinznsolves

whereqsatis fi esqn=1.It implies that the solutions order of(1.7)may take arbitrary numbers andP(z)2=n2z2(n-1)is not a constant.

Example 2We can construct a general solution from Example 1.Entire functionf(z)=sin(h(z))solves

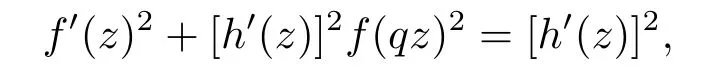
whereqsatis fi esqn=1 andh(z)is a non-constant polynomial.

Example 3Functionf(z)=sinhzis also an entire solution off′(z)2-f(qz)2=1 andf(z)=coshzis an entire solution off′(z)2-f(qz)2=-1,whereq=-1.

From Example 1 to Example 3,we also remark that ifP(z)2=±1,the transcendental entire solutionsf(z)are of order one,ifP(z)=nz(n-1),the transcendental entire solutionsf(z)are of ordern.Hence,it is reasonable to conjecture that the order of entire solutions of(1.7)is equal toρ(f)=1+degP(z).In this paper,we will answer the above conjecture and obtain the following result.

Theorem 1.1If|q＞|1,then the entire solution of(1.7)should be a polynomial.If there exists a fi nite order transcendental entire solutionfof(1.7),thenρ(f)=1+degP(z)and|q|=1.

In the following,we will consider anotherq-di ff erence di ff erential equation

and obtain the following result.

Theorem 1.2If|q＞|1,then the entire solution of(1.8)should be a polynomial.If there exist a fi nite order transcendental entire solutionfof(1.8),thenρ(f)=1+degP(z)and|q|=1.

Example 4Functionf(z)=sinzis an entire solution off′(z+c)2+f(qz)2=1,wherec=πandq=-1.

Finally,we consider otherq-di ff erence equation

Theorem 1.3If|q＞|1,then the entire solutionf(z)of(1.9)should be a polynomial.

IfP(z)2=1 in(1.9),the following example shows that we can not give the precise expression of fi nite order entire solution and the order off(z)does not satisfyρ(f)=1+degP(z)and|q|=1.

Example 5[11]Ifq=-1,,thusf(z)=sinzsatis fi es,thus

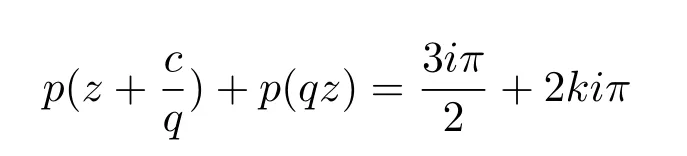
andkis an integer.Thus

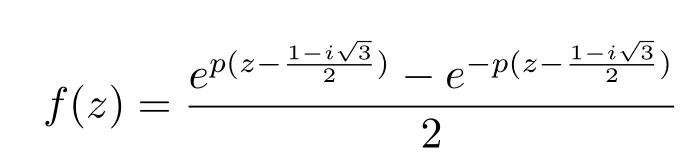
satis fi es

Remark 1The proofs of Theorem 1.2 and Theorem 1.3 are similar as the proof of Theorem 1.1.Hence we will not give the details here.

2 Some Lemmas

For the proofs of Theorems 1.1,1.2 and 1.3,we need the following results.

Lemma 2.1[3,Lemma 3.1]Let：(1,∞)→(0,∞)be a monotone increasing function,and letfbe a nonconstant meromorphic function.If for some real constantα∈(0,1),there exist real constantsK1＞0 andK2≥1 such that

then

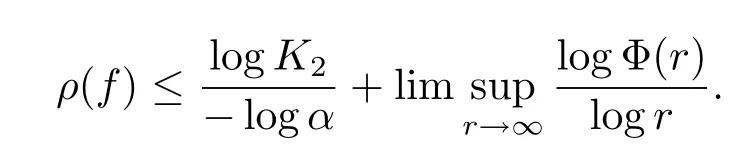
Lemma 2.2[11,Lemma 2.15]Letp(z)be a non-zero polynomial with degreen.Ifp(qz)-p(z)is a constant,thenqn=1 andp(qz)≡p(z).Ifp(qz)+p(z)is a constant,thenqn=-1 andp(qz)+p(z)≡2a0,wherea0is the constant term ofp(z).

Lemma 2.3[2,Theorem 2.1]Letf(z)be transcendental meromorphic function of fi nite orderρ.Then for anyε＞0,we have

Lemma 2.4[16,Theorem 1.62]Letfj(z)be meromorphic functions,fk(z)(k=1,2,···,n-1)be not constants,satisfyingand

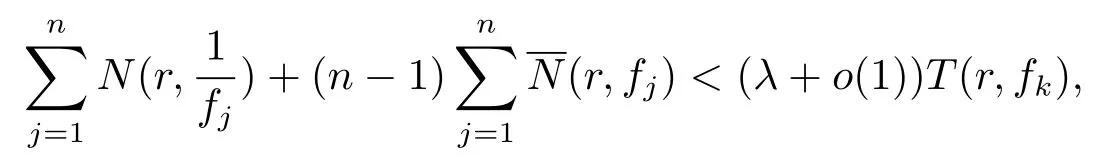
whereλ＜1 andk=1,2,···,n-1,thenfn(z)≡ 1.

3 Proof of Theorem 1.1

If|q＞|1 andf(z)is an entire solution of(1.7),we use the observation(see[1])that

holds for any meromorphic functionfand any constantq.Iff(z)is a transcendental entire function,then from(1.7)and Valiron-Mohon’ko theorem,we have

Letα=and|q＞|1.Then we have

Hence,we haveT(r,f(z))≤T(αr,f(z))+S(αr,f(z)).From Lemma 2.1,we haveρ(f)=0.Combining Hadamard factorization theorem,we havef′(z)+iP(z)f(qz)=Q1(z)andf′(z)-iP(z)f(qz)=Q2(z),thusis a polynomial,which is a contradictio n withf(z)is a transcendental entire function.Thusf(z)should be a polynomial.

Assume thatf(z)is a transcendental entire solution of(1.7)with fi nite order,then

Thus bothf′(z)+iP(z)f(qz)andf′(z)-iP(z)f(qz)have fi nitely many zeros.Combining(3.1)with the Hadamard factorization theorem,we assume that

and

whereh(z)is a non-constant polynomial provided thatf(z)is of fi nite order transcendental andQ1(z)Q2(z)=Q(z),whereQ1(z),Q2(z)are non-zero polynomials.Thus we have

and

From(3.2),we have

Taking fi rst derivative of(3.3),we have

where

and

From(3.4)and(3.5),we have

Obviously,ifh(qz)is a constant,thenh(z)is a constant,thusf(z)should be a polynomial.Ifh(qz)is a non-constant entire function,thenh(qz)-h(z)andh(qz)+h(z)are not constants simultaneously.The following,we will discuss two cases.

Case 1Ifh(qz)-h(z)is not a constant,from Lemma 2.4,we know that

Sincef(z)is a fi nite order entire solution,thenh(z)should satis fi esh(z)=anzn+···+a0is a non-constant polynomial,thus|q|=1 follows for avoiding a contradiction.From Lemma 2.2,we haveh(qz)+h(z)=2a0.Hence,we have

In addition,from(3.8),we also get

which implies that

Thus

Substitute(3.6)and(3.7)into(3.13),we have

Sincef(z)is a fi nite order entire solution,by comparing with the degree of both hand side of(3.14),we have

It implies thatρ(f)=1+degP(z).

Case 2Ifh(qz)+h(z)is not a constant,from Lemma 2.4,we know that

Hence|q|=1 follows for avoiding a contradiction.Assume thath(z)=anzn+···+a0,thush(qz)=h(z).Hence we have

In addition,from(3.8),we also get

Thus,similar as the above,we also getρ(f)=1+degP(z).

[1]Bergweiler W,Ishizaki K,Yanagihara N.Meromorphic solutions of some functional equations[J].Meth.Appl.Anal,1998,5：248-258.

[2]Chiang Y M,Feng S J.On the Nevanlinna characteristic off(z+η)and di ff erence equations in the complex plane[J].Ramanujan.J.,2008,16：105-129.

[3]Gundensen G,Heittokangas J,Laine I,Rieppo J,Yang D G.Meromorphic solutions of generalized Schr¨oder equations[J].Aequations Math.,2002,63：110-135.

[4]Halburd R G,Korhonen R J.Di ff erence analogue of the lemma on the logarithmic derivative with applications to di ff erence equations[J].J.Math.Anal.Appl.,2006,314：477-487.

[5]Hayman W K.Meromorphic functions[M].Oxford：Clarendon Press,1964.

[6]Laine I.Nevanlinna theory and complex di ff erential equations[M].Berlin,New York：Walter de Gruyter,1993.

[7]Liu K.Meromorphic functions sharing a set with applications to di ff erence equations[J].J.Math.Anal.Appl.,2009,359：384-393.

[8]Liu K,Cao T B,Cao H Z.Entire solutions of Fermat type di ff erential-di ff erence equations[J].Arch.Math.,2012,99：147-155.

[9]Liu K,Yang L Z,Liu X L.Existence of entire solutions of nonlinear di ff erence equations[J].Czech.Math.J.,2011,61(2)：565-576.

[10]Liu K,Yang L Z.On entire solutions of some di ff erential-di ff erence equations[J].Comput.Meth.Funct.Theory,2013,13：433-447.

[11]Liu K,Cao T B.Entire solutions of Fermat type di ff erence di ff erential equations[J].Electron.J.Di ff.Equ.,2013,2013：1-10.

[12]Liu K,Yang L Z.Some results on complex di ff erential-di ff erence theory[J].J.Math.,2013,33(5)：830-836.

[13]Tang J F,Liao L W.The transcendental meromorphic solutions of a certain type of nonlinear di ff erential equations[J].J.Math.Anal.Appl.,2007,334：517-527.

[14]Yang C C,Laine I.On analogies between nonlinear di ff erence and di ff erential equations[J].Proc.Japan Acad.,Ser.A,2010,86：10-14.

[15]Yang C C,Li P.On the transcendental solutions of a certain type of nonlinear di ff erential equations[J].Arch.Math.,2004,82：442-448.

[16]Yang C C,Yi H X.Uniqueness theory of meromorphic functions[M].Nederland：Kluwer Academic Publishers,2003.

[17]Zhang J L,Korhonen R J.On the Nevanlinna characteristic off(qz)and its applications[J].J.Math.Anal.Appl.,2010,369：537-544.

费马q-差分微分方程整函数解的增长性研究

刘新玲,刘 凯

(南昌大学数学系,江西南昌 330031)

本文研究了费马q-差分微分方程的整函数解的相关问题.利用经典和差分的Nevanlinna理论和函数方程理论的研究方法,获得了q-差分微分方程整函数解增长性的几个结果.

q-差分微分方程;整函数解;有穷级

O174.5

on：30D35;39B32;34M05

A Article ID： 0255-7797(2017)04-0761-08

date：2013-10-21Accepted date：2014-02-25

Supported by the NSFC(11301260;11101201);the NSF of Jiangxi(20132BAB211003)and the YFED of Jiangxi(GJJ13078).

Biography：Liu Xinling(1982-),female,born at Jinan,Shandong,instructor,major in complex analysis.