关于square-full数上的函数的均值估计
2017-07-18丽傅
杨 丽傅 春
(1.南昌大学管理学院,江西南昌 330031)(2.南昌大学理学院,江西南昌 330031)(3.南昌大学中国中部经济社会发展研究中心,江西南昌 330031)
杨 丽1,2,3,傅 春3
(1.南昌大学管理学院,江西南昌 330031)(2.南昌大学理学院,江西南昌 330031)(3.南昌大学中国中部经济社会发展研究中心,江西南昌 330031)
本文研究了指数k-free数的特征函数在square-full数集中的均值估计问题.利用黎曼Zeta函数的性质以及留数定理,获得了该均值的渐近公式,推广了在整数集中的均值估计相关结果.
square-full数;留数定理;除数问题;Dirichlet卷积;均值
1 引言
整数n>1有标准分解形式:若满足其中a1≥k,a2≥k,···,ar≥k,则称正整数n为k-full数,当k=2时也称为square-full数.令fk(n)是k-full数的特征函数,即

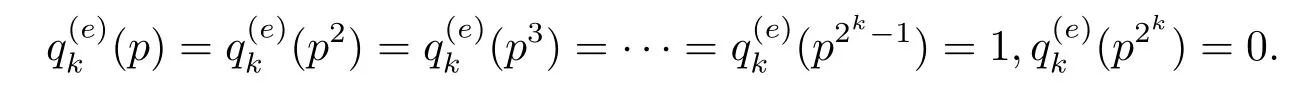
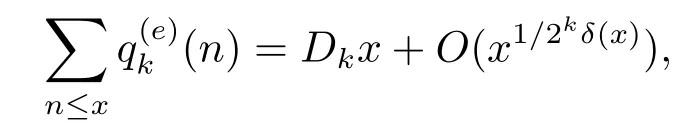
这里
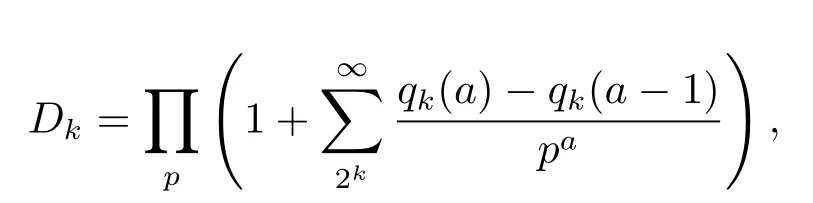

的渐近公式.即得到下面的定理.
定理当D>0时,对k≥3,有
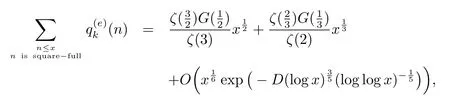
注本文中,表示一个任意小的的正常数,在不同的式中不必相同.
2 定理的证明
为了证明定理,需要以下的一些引理.
引理1 设a,b是整数,且1≤a<b,定义
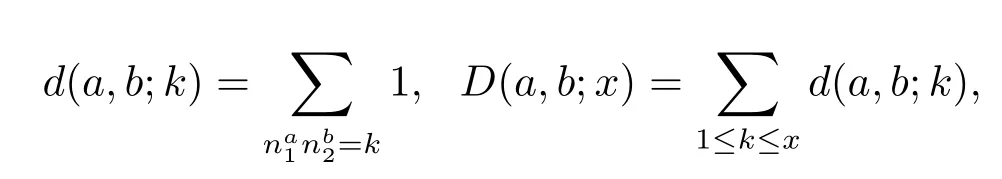
有
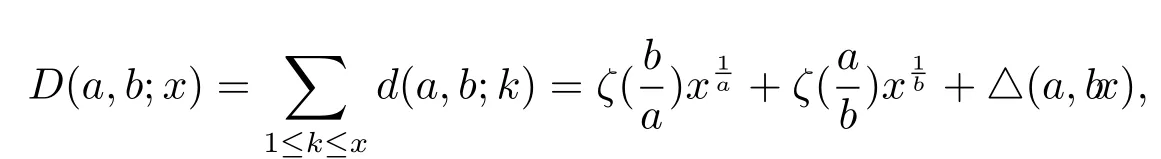
其中
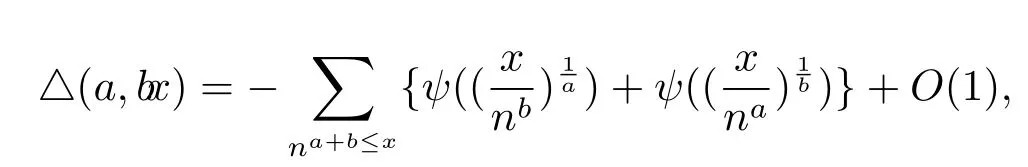
而且

证本引理的证明见Iv文[2]中的第14.3节和定理14.4.
引理2假设f(n)是算术函数,满足
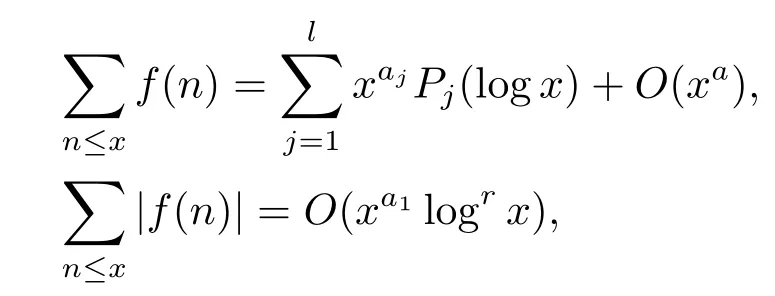
其中
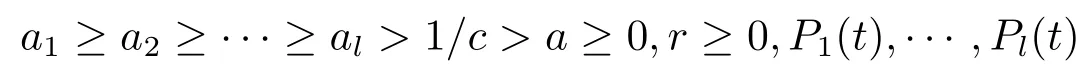
是关于t的次数不超过r的多项式,并且c≥1,b≥1是固定的整数.如果h(n)=,那么
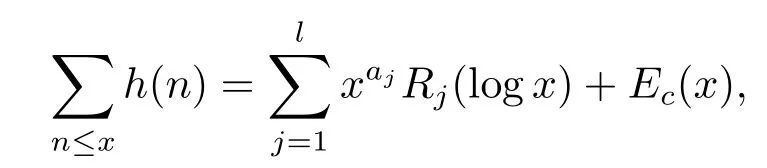
其中R1(t),···,Rl(t)是关于t的次数不超过r的多项式,并且当D>0时,有
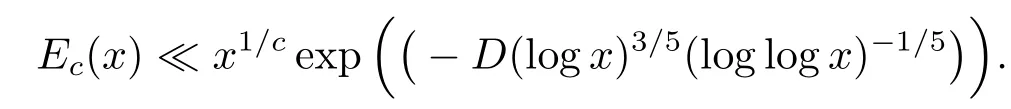
证见Iv文[2]中的定理14.2.
下面证明本文的定理.令
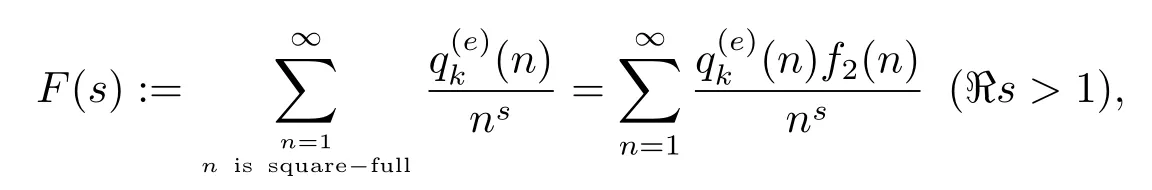
其中


其中
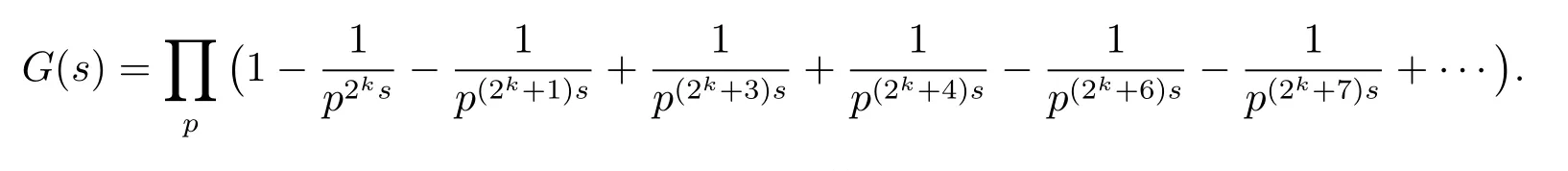
显然,对于k≥3,当时,G(s)绝对收敛.
根据卷积原理[3],定义
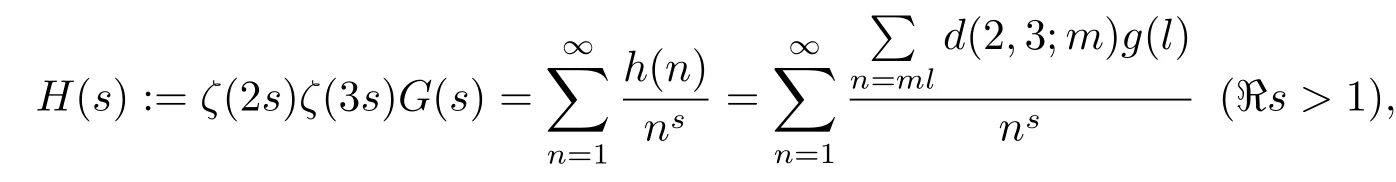

由引理1得到

很容易得到
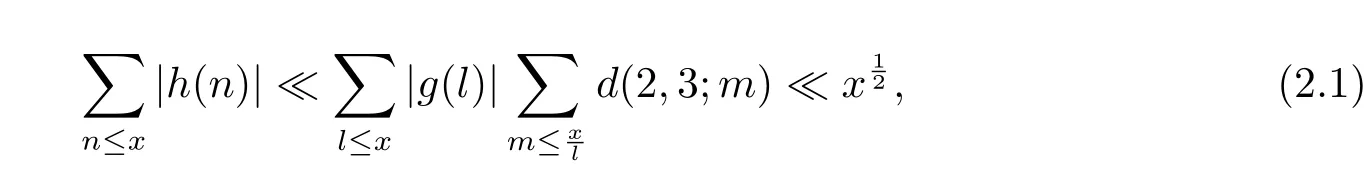
而且有
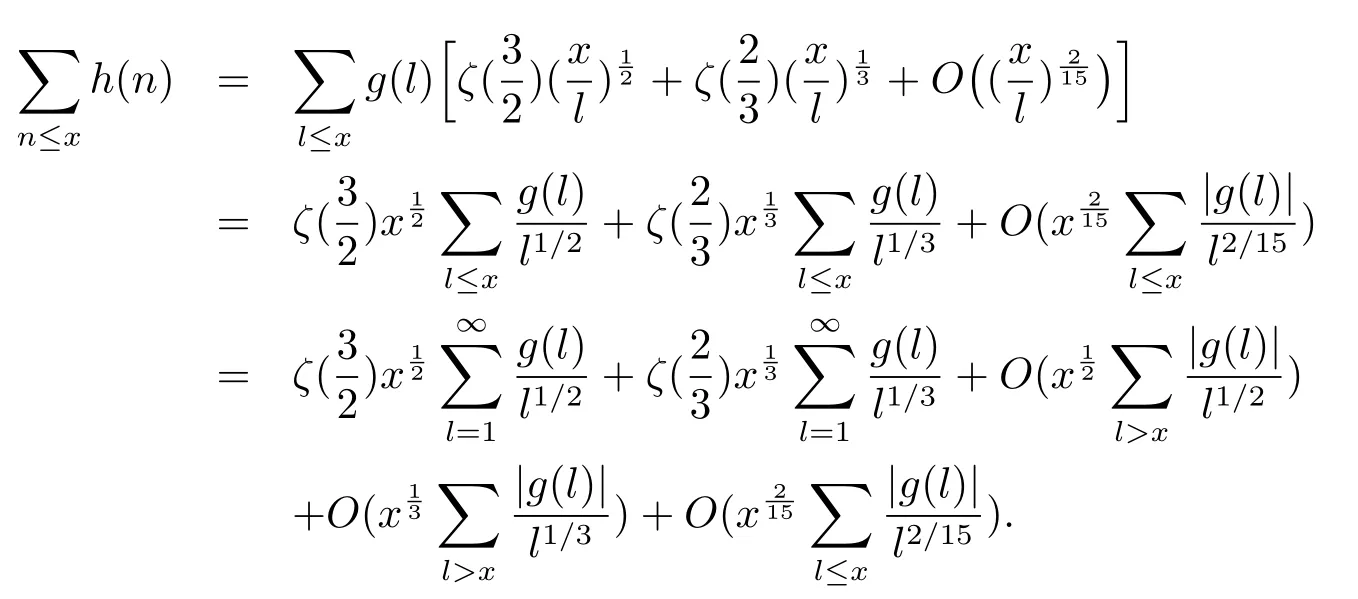
又由G(s)在ϵ时绝对收敛,则可设
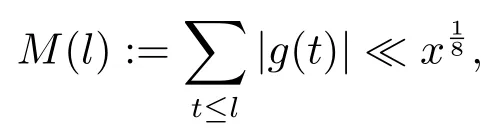
根据Abel分部求和得到

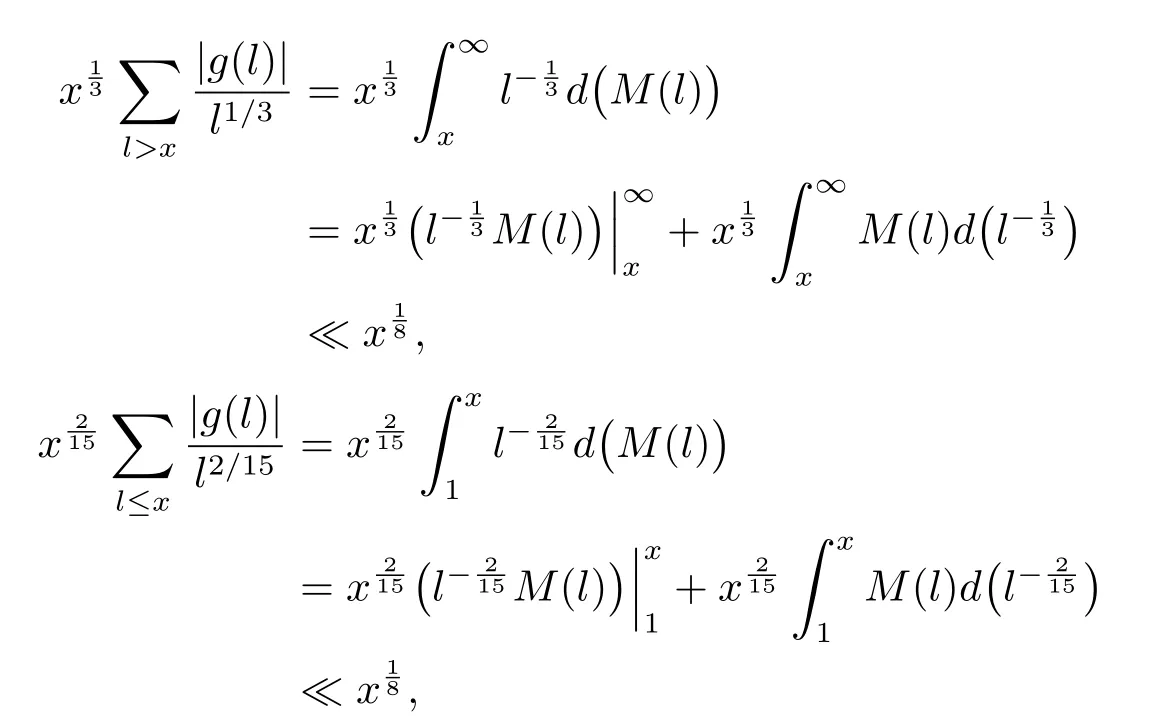
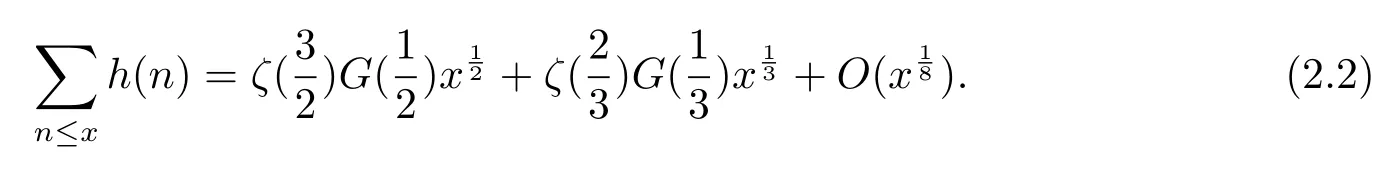
由于
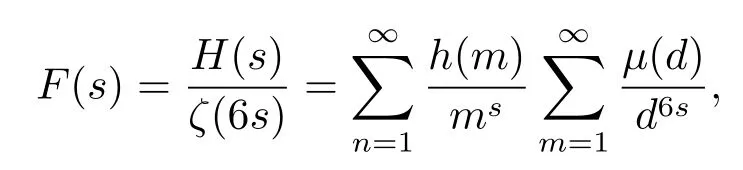
所以当n是square-full数时,有

再由Perron公式[3]可以得到

取T=x,并将积分线平移至处的留数分别为

再由(2.1)、(2.2)、(2.3)式和引理2,可以得到

其中D>0,并且G(s)当时是绝对收敛的.
这样就得到了本文的定理.
[1]贺艳峰,孙春丽.奇完全数的两个性质[J].数学杂志,2015,35(1):135-140.
[3]Subbarao M.V.On some arithmetic convolutions[J].The.Arith.Funct.,1972,251:247-271.
[4]Titchmarsh E.C.The theory of the Riemann Zeta-function[M].Oxford:Oxford University Press,1986.
THE MEAN VALUE OF FUNCTIONOVER SQUARE-FULL NUMBER
YANG Li1,2,3,FU Chun3
(1.School of Management,Nanchang University,Nanchang 330031,China)(2.School of Mathematics,Nanchang University,Nanchang 330031,China)(3.Center for Central China Economic Development Research,Nanchang University,Nanchang 330031,China)
In this paper,we study the mean value of the characteristic functionofk-free over square-full number.By using the property of Riemann-Zeta function and residue theorem,we obtain the asymptotic formula of the mean value,which is the generalization ofover integers.
square-full number;residue theorem;divisor problem;Dirichlet convolution;mean value
on:11E45
O156.4
A
0255-7797(2017)04-0865-06
2015-03-27接收日期:2015-10-28
南昌大学中国中部经济社会发展研究中心招标项目(15ZBLPS06);江西高校哲学社会科学研究重大课题攻关项目(ZDGG02);教育部哲学社会科学发展报告培育项目(13JBGP024).
杨丽(1982-),女,山东临沂,讲师,主要研究方向:应用数学.
猜你喜欢
杂志排行
数学杂志的其它文章
- k-NORMAL DISTRIBUTION AND ITS APPLICATIONS
- ROSSBY WAVES WITH THE CHANGE OFβAND THE INFLUENCE OF TOPOGRAPHY IN A TWO-LAYER FLUID
- ASYMPTOTIC PROPERTIES OF A CLASS OF NONLINEAR STOCHASTIC FUNCTIONAL DIFFERENTIAL EQUATIONS WITH INFINITE DELAY
- TOTALLY UMBILICAL SUBMANIFOLD ON RIEMANNIAN MANIFOLD WITH AN ORTHOGONAL CONNECTION
- ON A SINGULAR ELLIPTIC SYSTEM INVOLVING THE CAFFARELLI-KOHN-NIRENBERG INEQUALITY
- 一类λ-对数Bazilevic函数的Fekete-Szeg¨o不等式
