ON PROJECTIVE RICCI FLAT KROPINA METRICS

CHENG Xin-yue,MA Xiao-yu,SHEN Yu-ling

(School of Mathematics and Statistics,Chongqing University of Technology,Chongqing 400054,China)

ON PROJECTIVE RICCI FLAT KROPINA METRICS

CHENG Xin-yue,MA Xiao-yu,SHEN Yu-ling

(School of Mathematics and Statistics,Chongqing University of Technology,Chongqing 400054,China)

In this paper,we study and characterize projective Ricci fl at Kropina metrics.By using the formulas ofS-curvature and Ricci curvature for Kropina metrics,we obtain the formula of the projective Ricci curvature for Kropina metrics.Based on this,we obtain the necessary and sufficient conditions for Kropina metrics to be projective Ricci fl at metrics.Further,as a natural application,we study and characterize projective Ricci fl at Kropina metrics defined by a Riemannian metric and a Killing 1-form of constant length.We also characterize projective Ricci f l at Kropina metrics with isotropicS-curvature.In this case,the Kropina metrics are Ricci fl at metrics.

Finsler metric;Kropina metrics;Ricci curvature;S-curvature;projective Ricci curvature

1 Introduction

(α,β)-metrics form a special and very important class of Finsler metrics which can be expressed in the form),whereαis a Riemannian metric andβis a 1-from andφ=φ(s)is aC∞positive function on an open interval.In particular,whenφ=1+s,the Finsler metricF=α+βis called Randers metric.When,the Finsler metricis called Kropina metric.Randers metrics and Kropina metrics are bothC-reducible.However,Randers metrics are regular Finsler metrics and Kropina metrics are Finsler metrics with singularity.Kropina metrics were fi rst introduced by Berwald when he studied the two dimensional Finsler spaces with rectilinear extremal and were investigated by Kropina(see[4,5]).Kropina metrics seem to be among the simplest nontrivial Finsler metrics with many interesting application in physics,electron optics with a magnetic fi eld,dissipative mechanics and irreversible thermodynsmics(see[4,5,7]).Recently,some geometers found some interesting and important geometric properties of Kropina metrics(see[10-12]).

The Ricci curvature in Finsler geometry is the natural extension of the Ricci curvature in Riemannian geometry and plays an important role in Finsler geometry.A Finsler metricF=F(x,y)on ann-dimensional manifoldMis called an Einstein metric if it satis fi es the following equation on the Ricci curvatureRic

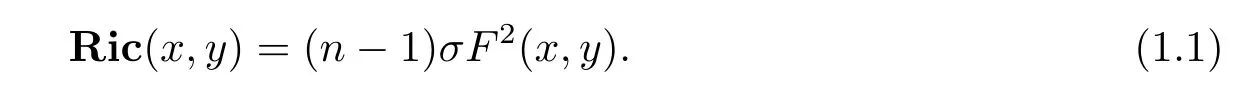
whereσ=σ(x)is a scalar function onM.In particular,a Finsler metricFis called a Ricci f l at metric ifFsatis fi es(1.1)withσ=0,that is,Ric=0.

TheS-curvatureS=S(x,y)is an important non-Riemannian quantity in Finsler geometry which was fi rst introduced by Shen when he studied volume comparison in Riemann-Finsler geometry(see[8]).Shen proved that theS-curvature and the Ricci curvature determine the local behavior of the Busemann-Hausdor ffmeasure of small metric balls around a point(see[9]).He also established a volume comparison theorem for the volume of metric balls under a lower Ricci curvature bound and a lowerS-curvature bound and generalized Bishop-Gromov volume comparison theorem in the Riemannian case(see[9]).Recent study shows that theS-curvature plays a very important role in Finsler geometry(see[2,9]).The Finsler metricFis said to be of isotropicS-curvature ifS(x,y)=(n+1)cF(x,y),wherec=c(x)is a scalar function onM.Further,ifc(x)=constant,thenFis said to be of constantS-curvature.

It is natural to consider the geometric quantities defined by Ricci curvature andS-curvature.Recently,Shen defined the concept of projective Ricci curvature in Finsler geometry.Concterely,for a Finsler metricFon ann-dimensional manifoldM,the projective Ricci curvaturePRicis defined by

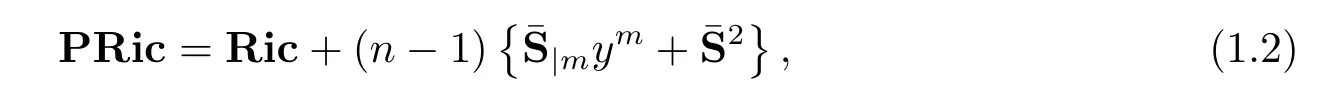
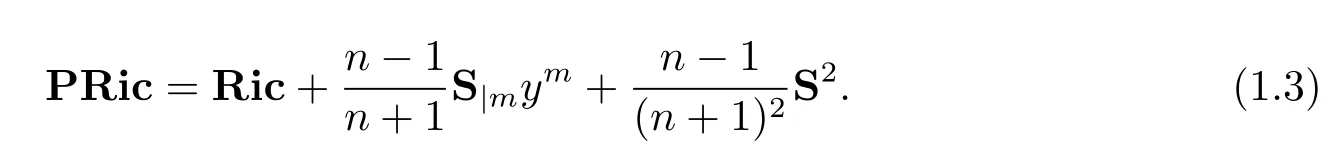
It is easy to show that,if two Finsler metrics are pointwise projectively related Finsler metrics on a manifold with a fi xed volume form,then their projective Ricci curvature are equal.In other words,the projective Ricci curvature is projective invariant with respect to a fi xed volume form.

On the other hand,the projective Ricci curvature is actually a kind of weighted Ricci curvatures.See[6]and the de fi nition ofS-curvature in Section 2.We call a Finsler metricFthe projective Ricci fl at metric ifFsatis fi esPRic=0.In[1],the authors characterized projective Ricci fl at Randers metrics.

To state our main results,let us introduce some common notations for Kropina metrics.Letbe a Kropina metric on ann-dimensional manifoldM.Put

where “ ;” denotes the covariant derivative with respect to the Levi-Civita connection ofα.Further,put

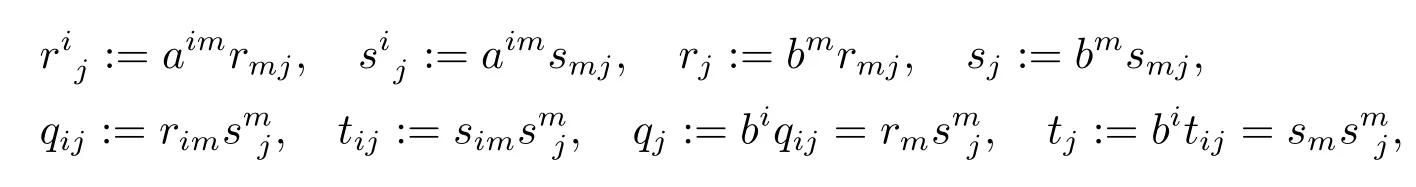
where(aij) ：=(aij)-1andbi：=aijbj.We will denoteri0：=rijyj,si0：=sijyjandr00：=rijyiyj,r0：=riyi,s0：=siyi,etc..

In this paper,by using Busemann-Hausdor ffvolume form,we will derive fi rstly the formula for the projective Ricci curvature of a Kropina metric in Section 3.Based on this,we can prove the following main theorem.

Theorem 1.1Letbe a Kropina metric on ann-dimensional manifoldM.ThenFis a projective Ricci fl at metric if and only ifαandβsatisfy the following equations

whereb：=‖βx‖αdenotes the length ofβwith respect toαand

By the de fi nition,the 1-formβis said to be a Killing form on Riemannian manifold(M,α)ifrij=0.The 1-formβis said to be a constant length Killing 1-form if it is a Killing form and has constant length with respect toα,equivalentlyrij=0 andsi=0.

For a Kropina metricF=α2/β,ifβis a constant length Killing 1-form with respect toα,we have the following theorem.

Theorem 1.2Letbe a Kropina metric with constant length Killing formβon ann-dimensional manifoldM.ThenFis a projective Ricci fl at metric if and only if there exists a functionλ=λ(x)such thatαis an Einstein metricαRic=λα2andβsatis fi es the following equations

For 1-formβ=bi(x)yionM,we say thatβis a conformal form with respect toαif it satis fi esbi;j+bj;i=ρaij,whereρ=ρ(x)is a function onMand “;” is the horizontal covariant derivative with respect toα.Ifρ=0,βis just a Killing form with respect toα.

In fact,for a Kropina metricF,the following four conditions are equivalent(see[10])：

(a)Fhas an isotropicS-curvature,S=(n+1)cF,wherec=c(x)is a function onM;

(b)r00=k(x)α2,wherek=k(x)is a function onM;

(c)S=0;

(d)βis a conformal form with respect toα.

So we can get the following conclusion.

Corollary 1.3Letbe a Kropina metric on ann-dimensional manifoldM.Assume thatFis of isotropicS-curvature,i.e.,S=(n+1)cF.ThenFis a projective Ricci fl at metric if and only ifFis Ricci fl at metric.

2 Preliminaries

LetFbe a Finsler metric on ann-dimensional manifoldMandGibe the geodesic coefficients ofF,which are defined by

For anyx∈Mandy∈TxM{0},the Riemann curvatureis defined by

The Ricci curvature is the trace of the Riemann curvature,which is defined byRic=Rmm.

For a Finsler metricF=F(x,y)on ann-dimensional manifoldM,define the Busemann-Hausdor ffvolume form ofFbydVF=σF(x)dx1∧dx2∧···∧dxn,where

and Vol denotes the Euclidean volume andBn(1)denotes the unit ball inRn.Then theS-curvatureSofFis given by

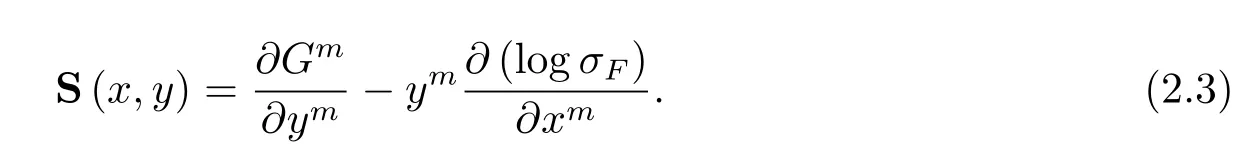
TheS-curvatureSmeasures the average rate of change of(TxM,Fx)in the directiony∈TxM.It is known thatS=0 for Berwald metrics.

(α,β)-metrics form an important class of Finsler metrics which can be expressed in the formis a Riemannian metric andβ=bi(x)yiis a 1-from with‖β‖α＜b0on a manifold.It was proved thatF=αφ(β/α)is a positive de fi nite Finsler metric if and only ifφ=φ(s)is a positiveC∞positive function on(-b0,b0)satisfying the following condition(see[2]),where

Randers metricF=α+βis just the(α,β)-metric withφ=1+s.Whenφ=1/s,the metricis just the Kropina metric.It is easy to see that a Kropina metricis not a regular Finsler metric for|s|＜b,but it is regular ifs＞0.In this paper,we study regular Kropina metrics.Hence,we will always restrict our consideration to the domain whereβ=bi(x)yi＞0 so thats＞0.

LetGi(x,y)andαGi(x,y)denote the geodesic coefficients of an(α,β)-metricF=αφ(β/α)andα,respectively.We can express the geodesic coefficientsGias follows(see[2]).

where

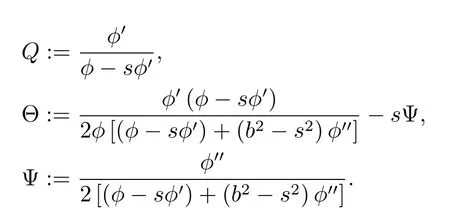
In particular,for a Kropina metric,it follows from(2.5)that

Further,the Ricci curvature ofis given by(see[12])

which is proved by Zhang and Shen(see Proposition 5.1 in[12]).

3 Projective Ricci Flat Kropina Metrics

In this section,we will fi rst derive a formula for the projective Ricci curvature of a Kropina metric.Then we will characterize projective Ricci fl at Kropina metrics.By(1.3),the projective Ricci curvature is given by

By(2.6),we have

Thus

From(2.8),we obtain

Further,we have

Substituting(2.7),(3.6)and(3.7)into(3.1),we obtain the formula for projective Ricci curvature of Kropina metricas follows

Now we are in the position to prove Theorem 1.1.

Proof of Theorem 1.1The proof of the sufficient condition in Theorem 1.1 is trivial.We will mainly prove the necessary condition in Theorem 1.1.

Assume thatPRic=0,which is equivalent to 4b4β2×PRic=0.By(3.8),we obtain the following

The equation(3.9)is equivalent to the following equation

where

Rewrite(3.10)as

Becauseα2andβ2are relatively prime polynomials iny,by(3.14)and the de fi nition of,we know that there exist a scalar functionλ(x)such that

Then(3.9)can be simpli fi ed as

Sinceα2can’t be divided byβ,we see that(3.16)is equivalent to the following equations

First,di ff erentiating both sides of(3.17)with respect toyiyields

Contracting(3.19)withbigives

Removing the factorb2form(3.20),we obtain

By(3.18),we obtain

then rewrite(3.21)as following

This completes the proof of Theorem 1.1.

4 Applications

In this section,we will fi rstly study projective Ricci fl at Kropina metrics with constant lenght Killing 1-formβand prove Theorem 1.2.Letbe a non-Riemannian Kropina metric with constant length Killing 1-formβon ann-dimensional manifoldM,that isrij=0,sj=0.In this case,equation(3.8)simplely as follows

Assume thatPRic=0,which is equivalent to 4β2×PRic=0.By(4.1),we obtain the following

ThusαRicis divisible byα2,that is,there exists a functionλ(x)such that

Plugging(4.3)into(4.2)and dividing the common factorα2,we conclude that

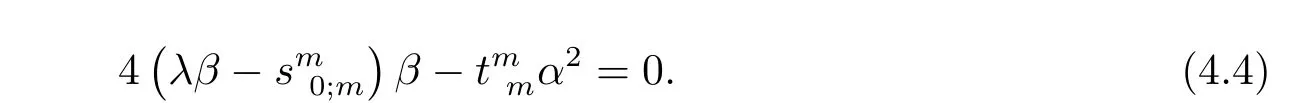
Sinceα2can not be divided byβ,we see that(4.4)is equivalent to the following equations

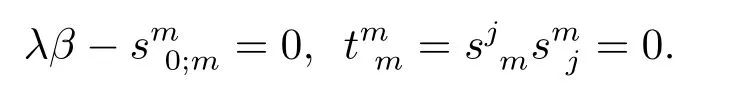
This completes the proof of Theorem 1.2.

Now,let us consider projective Ricci fl at Kropina metrics with isotropicS-curvature.As we mentioned in Section 1,a Kropina metricFis of isotropicS-curvature,S=(n+1)cF,if and only ifS=0.In this case,from the equation(1.3),we know that

Hence,Fis projective Ricci fl at metric if and only ifFis Ricci fl at metric.

In[12],Zhang and Shen proved that every Einstein-Kropina metrichas vanishingS-curvature.In this case,PRic=Ric.They also have obtained the necessary and sufficient conditions for Kropina metrics to be Einstein metrics in[12].

[1]Cheng Xinyue,Shen Yuling,Ma Xiaoyu.On a class of projective Ricci fl at Finsler metrics[J].Publ.Math.Debrecen,2017,90(1-2)：169-180.

[2]Cheng Xinyue,Shen Zhongmin.A class of Finsler metrics with isotropicS-curvature[J].Israel J.Math.,2009,169(1)：317-340.

[3]Cheng Xinyue,Zhang Ting,Yuan Min’gao.On dually fl at and conformally fl at(α,β)-metrics[J].J.Math.,2014,34(3)：417-422.

[4]Kropina V K.On projective two-dimensional Finsler spaces with a special metric[J].Trudy Sem.Vektor.Tenzor.Anal.,1961,11：277-292.

[5]Kropina V K.On projective Finsler spaces with a certain special form[J].Naun.Doklady Vyss.Skoly,Fiz.-Mat.Nauki,1959,2：38-42(in Russian).

[6]Ohta S.Finsler interpolation inequalities[J].Calc.Var.Partial Di ff.Equ.,2009,128：211-249.

[7]Shibata C.On Finsler spaces with Kropina metric[J].Rep.Math.Phys.,1978,13：117-128.

[8]Shen Zhongmin.Volume comparison and its applications in Riemann-Finsler geometry[J].Adv.Math.,1997,128：306-328.

[9]Shen Zhongmin.Lectures on Finsler geometry[M].Singapore：World Sci.Co.,2001.

[10]Xia Qiaoling.On Kropina metrics of scalar fl ag curvature[J].Di ff.Geom.Appl.,2013,31：393-404.[11]Yoshikawa R,Sabau S V.Kropina metrics and Zermelo navigation on Riemannian manifolds[J].Geom.Dedicata,2014,171(1)：119-148.

[12]Zhang Xiaoling,Shen Yibing.On Einstein Kropina metrics[J].Di ff.Geom.Appl.,2013,31：80-92.

射影Ricci平坦的Kropina度量

程新跃,马小玉,沈玉玲

(重庆理工大学数学与统计学院,重庆 400054)

本文研究和刻画了射影Ricci平坦的Kropina度量.利用Kropina度量的S-曲率和Ricci曲率的公式,得到了Kropina度量的射影Ricci曲率公式.在此基础上得到了Kropina度量是射影Ricci平坦度量的充分必要条件.进一步,作为自然的应用,本文研究和刻画了由一个黎曼度量和一个具有常数长度的Killing 1-形式定义的射影Ricci平坦的Kropina度量,也刻画了具有迷向S-曲率的射影Ricci平坦的Kropina度量.在这种情形下,Kropina度量是Ricci平坦度量.

芬斯勒度量;Kropina度量;Ricci曲率;S-曲率;射影Ricci曲率

O186.1

on：53B40;53C60

A Article ID： 0255-7797(2017)04-0705-09

date：2015-07-16Accepted date：2015-11-09

Supported by the National Natural Science Foundation of China(11371386)and the European Union’s Seventh Framework Programme(FP7/2007-2013)under grant agreement(317721).

Biography：Cheng Xinyue(1958-),male,born at Chongqing,professor,major in di ff erential geometry and its applications.