双渠道回收闭环供应链演化博弈复杂性与控制

于 淼, 马军海

(天津大学管理与经济学部，天津300072)

双渠道回收闭环供应链演化博弈复杂性与控制

于 淼, 马军海

(天津大学管理与经济学部，天津300072)

构建了一个由制造商与零售商同时回收废旧电子产品的闭环供应链模型，拟分析新产品与再制品差别定价销售行为的市场运营模式。运用博弈论、混沌动力学和复杂动力学理论，结合数值实验计算进行理论验证和现实仿真方法。研究表明，制造商和零售商的决策变量调节速度过快时，均会使得系统陷入一种混沌无序的状态。鉴于混沌系统的危害，采用调整参数可以对混沌进行了有效的控制，研究具有很好的理论和实际应用价值。

闭环供应链；混合回收渠道；演化博弈；混沌

0 引言

随着中国经济的不断稳定快速发展，生产所造成的废旧品受到越来越多的关注。生活水平的提高、人民对生活质量要求的提高，使得很多产品没有达到其使用寿命时就被丢弃，大量的废旧品不但对于环境有很大的损害，而且是一种很大的资源浪费，如何合理有效地对废旧品进行回收再利用，成为当今广为关注的问题。针对此问题，很多国家都出台了相应的政策与法律法规来提高原材料的重复利用率，推进循环经济的发展。如今，越来越多的企业将闭环供应链管理纳入企业的战略管理中。

目前，国内外的研究现状主要集中在3个方面。第一，闭环供应链的定价决策与协调机制。Liang Y J的团队[1]认为新产品与再制造商品的市场定价是不同的，再制品的零售价格遵循几何布朗运动，并在此基础上提出一个模型将再制品的收购价格与销售价格链接在一起。Chen J M与Chang C J[2]讨论了在何种情况下OEM应参与废旧品的回收以及再制造，分析表明，OEM做出的战略决策主要取决于再制造的成本以及第三方回收和OEM回收再制造之间的竞争强度。Maiti T等[3]建立了一个制造商通过零售商进行新产品与再制品的销售，并通过第三方进行废旧品回收的闭环供应链，市场中消费者的需求与新产品和再制品的质量有关。分别讨论了纳什博弈与3种不同领导者的斯坦科尔伯格博弈，并比较4种情况下的最优解。He Y[4]研究了需求不确定和供应不确定的闭环供应链，在集中决策和分散决策下回收价格和再制造的最优决策。结果表明，回收渠道的成本与供应渠道的成本相差越大，双重边际效应的影响越大。并通过数值模拟讨论了需求的不确定水平与供应的不确定水平对于闭环供应链中各个变量的影响。肖迪和黄培清[5]在闭环供应链中加入了EOQ模型，讨论了允许缺货和不允许缺货两种情况下基于产品时间价值的最优库存策略，以及随着时间推移，回收的废旧品的价值减少对于库存策略的影响。聂佳佳[6]分别讨论了制造商回收、零售商回收、第三方回收3种回收模式下的集中决策以及零售商分享和不分享信息下的分散决策，得出信息分享不利于零售商，却可在制造商回收时增加供应链利润，因此应建立信息分享补偿政策激励零售商。

第二，闭环供应链回收渠道的选择问题。Savaskan的团队[7]讨论了制造商选择不同的回收渠道(制造商回收、零售商回收、第三方回收)回收废旧品时在正向物流中产品的价格决策，并建立了制造商直接回收，同时零售商作为产品回收点进行间接回收的混合回收模式，讨论不同模式下制造商的经济权衡。结论是在直接回收渠道中，渠道利润由回收付出的规模影响，而在间接回收渠道中，供应链利润由零售商之间的相互竞争影响。Zu J M的团队[8]建立了一个制造商、一个零售商和两个回收站组成的三级供应链，讨论了不同的合作策略结构如何影响到闭环供应链的决策。结果发现，合作策略可以导致双赢的局面，提高合作者的利润，并从整条供应链的角度提高可以达到更高的效率。Huang M等人[9]讨论了双回收渠道的闭环供应链，在正向物流中，制造商通过零售商销售产品，而在逆向物流中，零售商与第三方同时竞争地收集废旧品。将双回收渠道的最优策略与单一回收渠道(零售商或第三方)的进行对比，分别从制造商的角度和消费者的角度推导出双回收渠道优于单一回收渠道时竞争强度的参数域。肖雪珣与陈晓荣[10]构建了由一个制造商和两个相互竞争的零售商组成的闭环供应链，分别研究并比较了在奖金制和押金制两种策略下的集中决策与分散决策。徐兵[11]建立了制造商开设直销渠道并进行回收再制造的双渠道闭环供应链，将分散决策与集中决策进行比较，并采取批发价合同对闭环供应链进行协调，结论发现闭环供应链中引入直销渠道既会吸引潜在客户，也会增大渠道运营的风险。

第三，将复杂动力系统理论应用于供应链模型中。Bischi GI和Kopel M[12]研究了成员具有预期回报的非线性离散型双寡头古诺博弈，分析了其均衡点选择问题，并表明其迭代结果具有初值敏感性。Akio M与Yasuo N[13]建立了两个厂商的简单动态古诺博弈模型，研究了混沌经济动态的统计学特征，结果显示，长期具有混沌轨道的平均利润高于稳定在一个点上的利润，表明混沌动力学在长远来看也许是有利的。Elsadany[14]建立了带有延迟的有限理性双寡头博弈，分析了其复杂性及均衡点的局部稳定性，结果表明采用延迟有限理性的厂商有更大的机会达到纳什均衡点。郭悦红及马军海等[15]研究了双寡头制造商的回收再制造重复博弈模型，采用复杂动力学分析均衡点的稳定性以及各参数对系统的影响，并提出控制方法。谢磊和马军海[16]选取了中国的废弃家电市场，采用复杂系统理论对一个制造商两个零售商组成的逆向物流进行了分析，并通过延迟决策对混沌进行控制。

由国内外文献可见，关于闭环供应链的研究，多是从单一回收渠道角度，并采用运筹学方法进行研究，然而随着市场竞争的加剧，制造商开始将部分回收业务委托给零售商或第三方回收。例如一些电子产品不仅通过零售商或第三方来回收产品，还会通过维修点或直接进行废品回收，可见混合渠道的回收已成为当今市场的特点，既可以促进销售与回收市场，亦可为消费者带来一定的福利。本文旨在采用复杂系统理论的方法，对制造商和零售商混合回收的闭环供应链进行研究。

1 模型的建立

1.1 模型建立与前提假设

闭环供应链的回收方式主要有3种，即制造商回收、零售商回收和第三方回收。而随着市场竞争的加剧，存在多种渠道同时回收的回收方式，本文研究的废旧品回收工作由制造商与零售商共同完成，其供应链循环方式由图1所示。

基于该闭环供应链系统，对本文的研究进行如下假设：

1) 假定消费者对产品的需求是线性的，需求量随销售价格升高而减小，反之亦然。同样，回收数量也是线性的，只与自身回收价格和竞争者回收价格有关，而不受环境，服务，消费水平等因素影响。

2) 假定制造商与零售商同时进行废旧品回收工作，且在回收中有竞争，各自的回收价格不但影响自身回收数量，也会影响对方回收数量。

3) 制造商进行废旧品回收再制造的单位成本低于制造新产品的单位成本，即制造商进行回收是有利可图的。

4) 新产品与再制品在外观上无差异，但由于市场中消费者对于再制品的认可度要低于对新产品的认可度，因而新产品的售价要高于再制品的售价。

5) 制造商的回收再制造能力无限制，但回收的废旧品并不能完全用于再制造，其中一部分回收品由于无利用价值而将其废弃。

6) 假设市场需求量大，仅依靠废旧品回收再制造不能满足市场需求。

7) 闭环供应链中的制造商和零售商都是独立的决策者，在离散的周期点t=0,1,2…分别进行各自的决策，决策的目标都是自身的利润最大化，但由于市场条件的约束，他们对于其他决策者的行为和市场中的状况并不能完全掌握，因而只能是有限理性地进行决策。

1.2 符号说明与模型建立

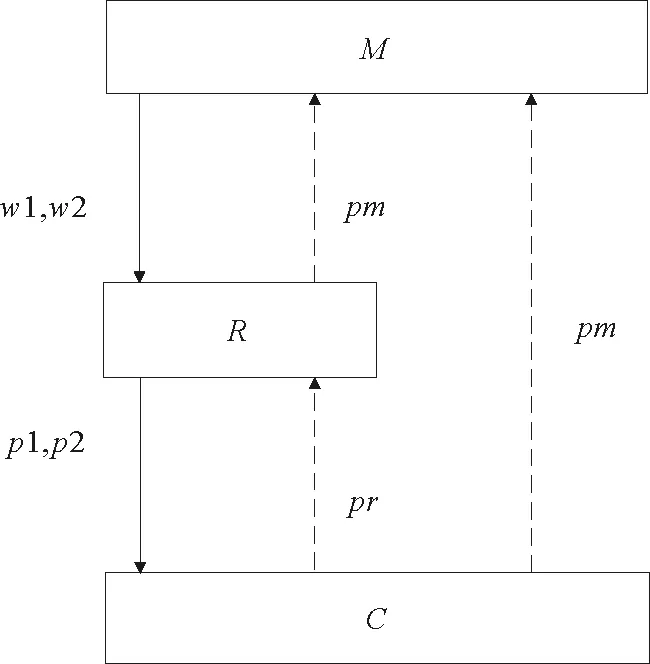
图1 双渠道回收的闭环供应链基本循环模式Fig.1 Dual-channel recycling closed-loop supply chain basic circular model

cn— 新产品的制造成本，为确定的常量。

cr— 与回收品的再制造成本，为常量，且满足cn>cr。

pr— 零售商的单位回收价格，为零售商的决策变量。

pm— 制造商直接回收的单位回收价格，为制造商的决策变量。

则制造商与零售商的回收量分别为

(1)

其中，k表示当制造商和零售商给消费者的单位回收价格为零时，消费者自愿返还的废旧品的数量，即消费者的环保意识。h1为消费者对于回收价格的敏感系数，h2为制造商与零售商回收价格的竞争系数，且满足h1≥h2。

w1— 新产品的批发价，为制造商的决策变量。

w2— 再制造品的批发价，为制造商的决策变量。

p1— 新产品的零售价。

p2— 再制造品的零售价。

r— 零售商的销售盈利率，为常量。则

(2)

D(p1)— 消费者对新品的需求量。

D(p2)— 消费者对再制品的需求量。

如再造品无价格优势则没有消费者愿意购买再造品，那么消费者对新品再造品的需求量分别为

(3)

制造商付给零售商的回收品的单位转移价格与制造商直接付给消费者的单位回收价格相等，亦为pm。

α— 废品的可利用率。

则制造商和零售商的利润模型分别为

πM=D(p1)(w1-cn)+D(p2)(w2-cr)+α(cn-cr-pm)(Qm+Qr)

(4)

πR=D(p1)(p1-w1)+D(p2)(p2-w2)+(pm-pr)Qr

(5)

由式(4)、(5)可见，制造商的决策变量为废旧品的单位回收及转移价格pm，以及新产品与再制造产品的单位批发价格w1、w2，零售商的决策变量为单位回收价格pr，由此得到的边际利润函数为

(6)

由于市场的纷繁复杂，制造商与零售商不能完全了解也无法准确预测市场的真实信息和其他决策者的全部信息，因此，市场中的决策者均采用有限理性的决策方式。在有限理性下决策者第t+1期的决策为

(7)

其中gi>0(i=1,2,3,4)分别表示零售商对于其回收价格pr、销售盈利率r以及零售商对于其回收价格pm、转移价格p0的调整速度。则由方程式(7)可得到四维离散动力系统：

(8)

1.3 模型分析

上文所建立的动力系统经过一定周期的博弈，决策变量经过不断调整，最终会达到一个均衡状态，在此状态下，博弈各方均不能通过改变决策变量的值而使自己的利润增加，因此，决策变量的值将不再调整，各方能够实现利润最大化。此时求得系统的均衡点为：

对于以上16个均衡点，可以看到只有R16是完全非零的，而R1～R15的均衡解中均不完全非零，在经济学中，决策者是不允许自己选择一个零值的决策变量，因而这13个均衡点均是不稳定的，只有R16是局部稳定的。下面通过求解各个均衡点的Jacobian矩阵来加以验证。

首先计算系统的雅克比(Jacobian)矩阵:

下面分别计算13个均衡点的Jacobian矩阵并根据特征值大小判断其稳定性，如非零特征值大于1，则该均衡点是不稳定的。以R1为例，其雅克比矩阵为

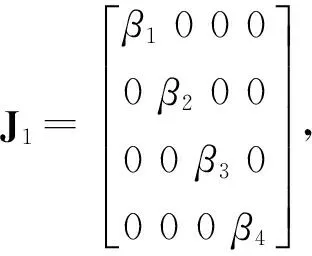
显然，特征值>1，为不稳定均衡解，同理,R1～R15均为不稳定的均衡解，只有R16是局部稳定的Nash均衡解，这也与上述经济学分析相符。

2 数值模拟

如今主要采用数值仿真的方法对复杂动力系统进行表征，本文应用Matlab软件对系统进行数值模拟，以分析其动力学特征。对系统中的参数赋值如下：k1=30,k2=50,cn=100,cr=60,h1=20,h2=10,α=0.5,λ1=1000,λ2=5。

本文将通过系统的混沌分岔图，最大Lyapunov指数，以及混沌吸引子3种方式展现系统的动态特征，以研究决策变量的调整速度对系统的影响，并分析系统中决策变量的初值敏感性。

2.1 混沌分岔现象

其他条件不变，当g2=0.005,g3=0.003,g4=0.004，在区间[0.006,0.009 5]变化时，制造商与零售商的回收价格变化如图2，图中可以看出，当在(0.006,0.007 62)时，系统处于稳定状态，经过多次博弈后，两个回收价格分别稳定在12.11和7.903，而当g1=0.007 62时系统会发生第一次分岔，接着会经过周期2，周期4……而逐步陷入混沌状态。

其他参数不变时，令g1=0.001,g3=0.001,g4=0.001，g2在区间[0.015,0.022]变化时，制造商与零售商的回收价格变化如图3，图中可以看出，当g2在(0.015,0.017 7)时，系统处于稳定状态，经过多次博弈后，两个回收价格分别稳定在12.12和7.807，而当g2=0.017 7时系统会发生第一次分岔，接着会经过周期2，周期4……而逐步陷入混沌状态。

其他参数不变时，令g1=0.000 1,g2=0.000 1,g4=0.000 5，g3在区间[0.000 7,0.001 45]变化时，制造商制定的新产品与再制造产品的批发价格变化如图4，图中可以看出，当在(0.000 7,0.000 94)时，系统处于稳定状态，经过多次博弈后，两个批发价格分别稳定在158和108.7，而当g3=0.000 94时系统会发生第一次分岔，接着会经过周期2，周期4……而逐步陷入混沌状态。

其他参数不变时，令g1=0.000 1,g2=0.000 1,g3=0.000 1，g4在区间[0.001 2,0.002 1]变化时，制造商制定的新产品与再制造产品的批发价格变化如图5，图中可以看出，当g4在(0.001 2,0.001 48)时，系统处于稳定状态，经过多次博弈后，两个批发价格分别稳定在157.8和109，而当g4=0.001 48时系统会发生第一次分岔，接着会经过周期2，周期4……而逐步陷入混沌状态。

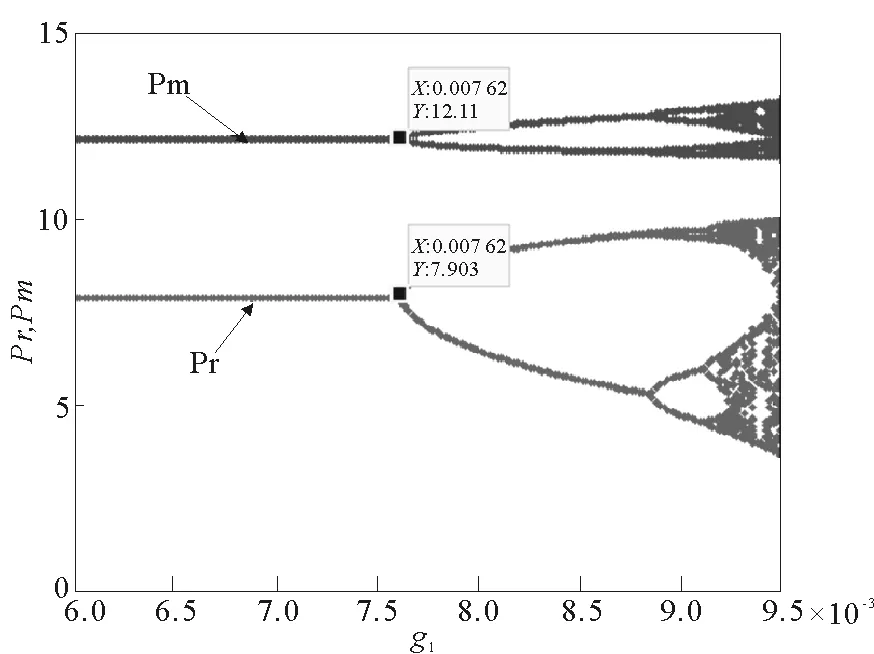
g2=0.005,g3=0.003,g4=0.004图2 回收价格随g1变化的动态演化图Fig.2 Recycling price dynamic changing with g1

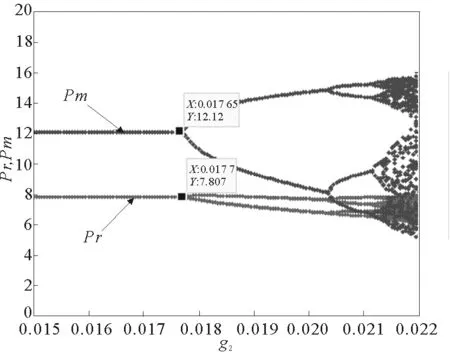
g1=0.001,g3=0.001,g4=0.001图3 回收价格随g2变化的动态演化图Fig.3 Recycling price dynamic changing with g2

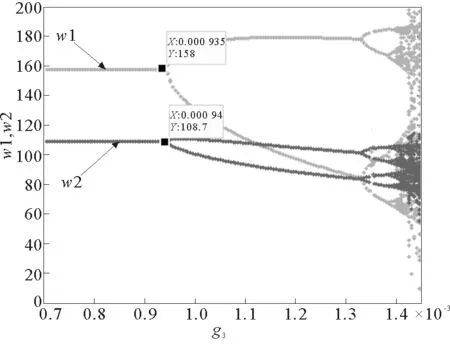
g1=0.000 1,g2=0.000 1,g4=0.000 5图4 批发价格随g3变化的动态演化图Fig.4 Wholesale price dynamic changing with g3

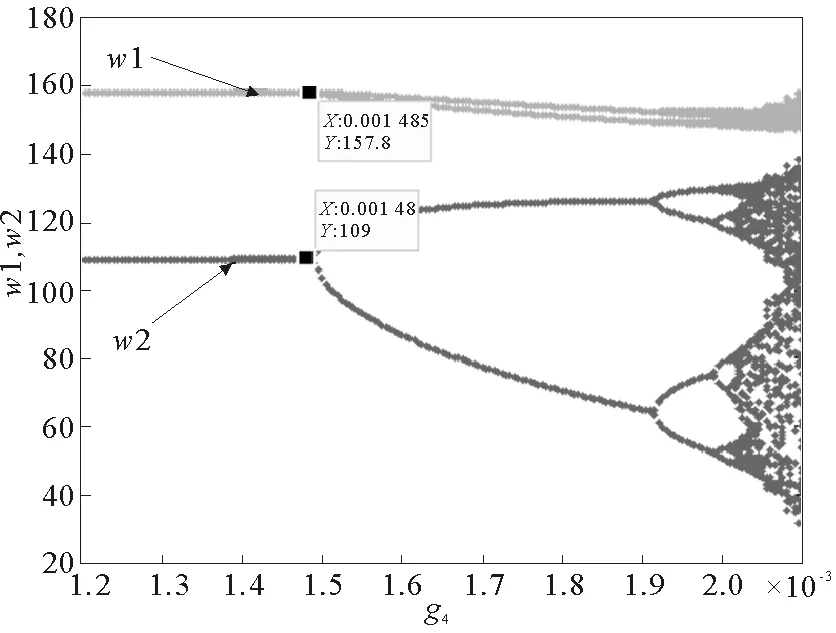
g1=0.000 1,g2=0.000 1,g3=0.000 1图5 批发价格随g4变化的动态演化图Fig.5 Wholesale price dynamic changing with g4

2.2 最大Lyapunov指数

当调整系统决策变量的变化速度时，系统的最大Lyapunov指数会产生动态变化，可以通过最大Lyapunov指数来分析系统的动态特征。当最大Lyapunov指数小于零时，系统处于稳定状态；当最大Lyapunov指数等于零时，系统处于周期运动或准周期运动；当最大Lyapunov指数大于零时，系统处于混沌状态。

下面，以g2和g4变化为例，分析系统的最大Lyapunov指数，当g1=0.001,g3=0.001,g4=0.001,g2在区间[0.015,0.022]变化；以及当g1=0.000 1,g2=0.000 1，g3=0.000 1,g4在区间[0.001 2,0.002 1]变化时，系统的最大Lyapunov指数如图6和7所示。将最大Lyapunov指数与分岔图相对应，可见系统发生分岔以及进入混沌的g值与分岔图中相吻合。

2.3 混沌吸引子

当系统稳定时，吸引子为稳定的不动点，而当系统陷入混沌时，混沌吸引子空间占有更大，结构更复杂。当g1=0.001,g2=0.022,g3=0.001,g4=0.001时，由分岔图可见系统为混沌状态，此时的混沌吸引子如图8所示。

g1=0.001,g3=0.001,g4=0.001图6 系统的最大Lyapunov指数Fig.6 The biggest Lyapunov exponent of system

g1=0.000 1,g2=0.000 1,g3=0.000 1图7 系统的最大Lyapunov指数Fig.7 The biggest Lyapunov exponent of system

g1=0.001,g2=0.022,g3=0.001,g4=0.001图8 系统的混沌吸引子Fig.8 Chaotic attractor

当g1=0.000 1,g2=0.000 1,g3=0.001 4,g4=0.000 5时，系统也陷入混沌状态，此时的混沌吸引子如图9所示。

由图2～图9可见，在制造商与零售商混合回收的闭环供应链中，系统的调节速度越快，企业对系统的反应越灵敏，市场越容易陷入混沌无序状态。当决策变量的初值给定时，系统的均衡点是不随决策变量的调整速度变化的，然而，调节速度的大小会影响到市场由有序变为无序的周期值。因此，制造商与零售商进行废旧品回收竞争时，不应该为了占据更大的回收市场份额、取得更大的回收利润而一味地提高回收品数量，制造商也不应该过快地调节新品与再造品的批发价格，而应该综合考虑市场的状况以及竞争对手的反应。

g1=0.000 1,g2=0.000 1,g3=0.001 4,g4=0.000 5图9 系统的混沌吸引子Fig.9 Chaotic attractor

2.4 初值敏感性

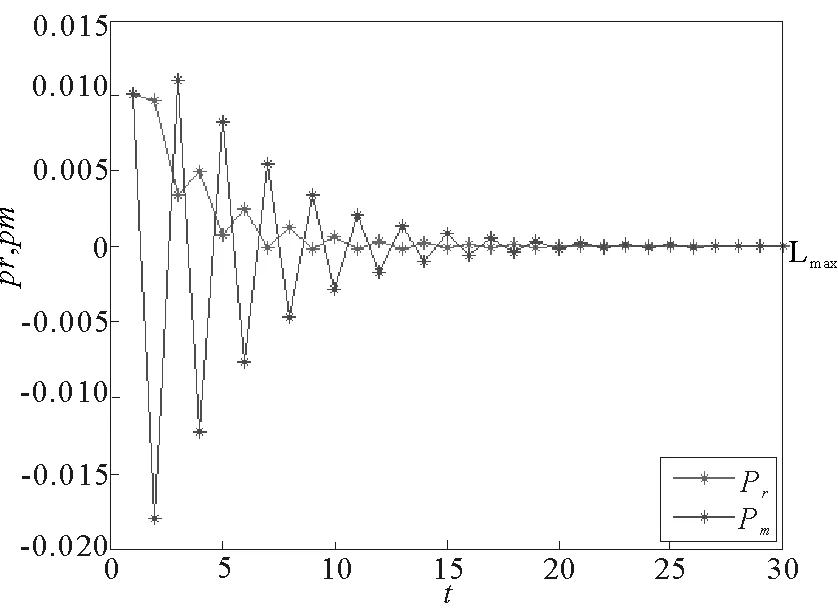
g1=0.001,g2=0.016,g3=0.001,g4=0.001图10 稳定系统对回收价格初值的敏感性Fig.10 The stable system is sensitive to initial value of recycling price

当g1=0.001,g2=0.016,g3=0.001,g4=0.001时，系统处于稳定状态，此时将回收价格的初值取相差0.01，经过30次迭代后的差值如图10，可见开始迭代时，存在一定的差值，大概迭代20周期后，差值逐渐减少为0。

而当g1=0.001,g2=0.022 3,g3=0.001,g4=0.001时，系统处于混沌状态，此时将每个决策变量都分别取两个相差0.01的初值，经过一定周期的博弈，初值变化前后的差值如图11～图14。由图11可以发现，当pr的初值改变0.01时，随着迭代次数的增加，当系统重复博弈大概25次时，两个pr的差值已经达到了1.088，是初值的一百倍。而在图12中，初值相差0.01的pm在系统迭代20次以后，更是相差了7.675，达到了初值的七百多倍。同样，从图13和图14，当批发价格的初值改变0.01时，随着博弈次数增加，差值也会增大到几十倍。

由此可见，混沌系统对于初值有很大的敏感性，初值的微小变动随着时间的推移会导致巨大的偏差，因此，需要决策者在选择决策变量初值时要更加谨慎。

3 混沌控制

由前文可知，混沌现象在经济系统中往往是有害的，所以要尽量在混沌发生以前对其进行预防，在混沌发生后对其进行控制。本文采用调整参数控制的方法。

未进行控制的动态离散系统可以表示为

g1=0.001,g2=0.022 3,g3=0.001,g4=0.001图11 混沌系统对回收价格初值的敏感性图Fig.11 Chaotic system is sensitive to initial value of recycling price

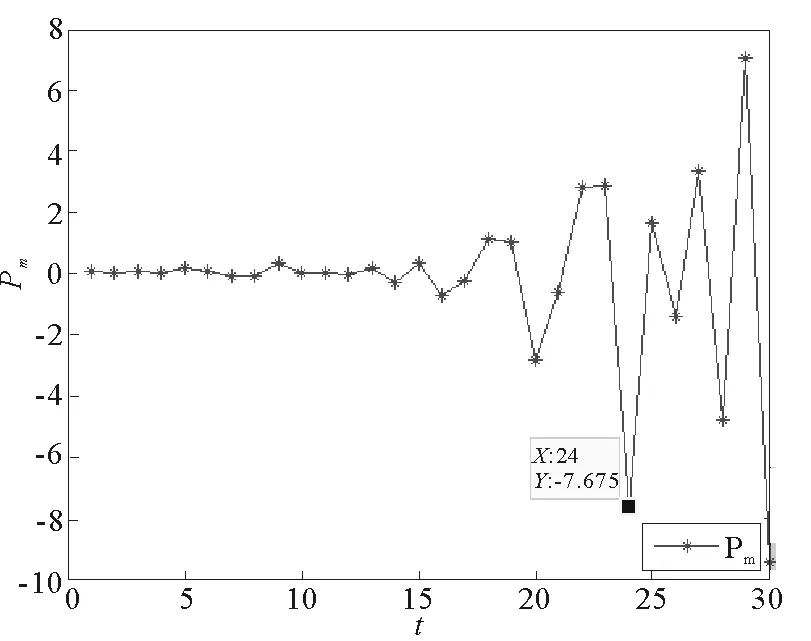
g1=0.001,g2=0.022 3,g3=0.001,g4=0.001图12 混沌系统对回收价格初值的敏感性Fig.12 Chaotic system is sensitive to initial value of recycling price

g1=0.001,g2=0.022 3,g3=0.001,g4=0.001图13 混沌系统对批发价格初值的敏感性Fig.13 Chaotic system is sensitive to initial value of wholesale price

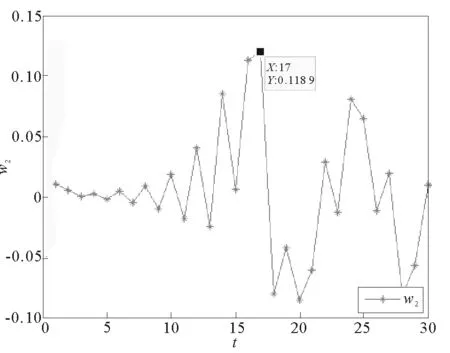
g1=0.001,g2=0.022 3,g3=0.001,g4=0.001图14 混沌系统对批发价格初值的敏感性Fig.14 Chaotic system is sensitive to initial value of wholesale price

对其进行参数调整后，控制系统可以表示为

研究调节参数u对混沌系统的控制作用，采用数值模拟的方式，又前文可知，当g1=0.001,g2=0.022,g3=0.001 2,g4=0.001时，系统处于混沌状态，加入调节参数u以后，随着调节参数的变化，系统的变量状况如图15和图16，可见u=0时整个系统为混沌状态，每个变量都是不可控的，随着u的增大，4个变量都由混沌状态逐渐到稳定状态，混沌得到了有效的控制。

由此可见，制造商和零售商都希望所处的市场是稳定的，这时的决策相对简单，可以在稳定中追求利润的最大化，然而闭环供应链的市场是很复杂的，决策变量的变化很可能使稳定的市场进入混沌状态，此时，就需要制造商和零售商联合起来，对混沌采取一定的控制措施，以达到延迟或消除混沌的目的，有利于整个市场的发展与稳定。

g1=0.001,g2=0.022,g3=0.001 2,g4=0.001图15 随调节参数u变化的系统分岔图Fig.15 The changes of adjustment parameter u of system bifurcation diagram

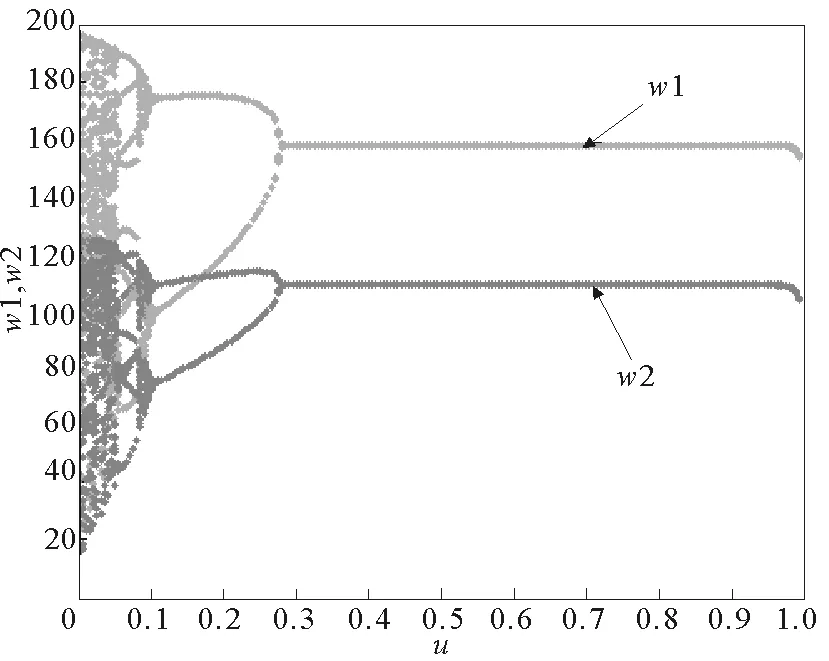
g1=0.001,g2=0.022,g3=0.001 2,g4=0.001图16 随调节参数u变化的系统分岔图Fig.16 The changes of adjustment parameter u of system bifurcation diagram

4 结论

本文研究了一个制造商与一个零售商同时进行废旧品回收组成的闭环供应链，制造商负责所有的制造与再制造，并且新产品与再制品有差价，制造商与零售商均以自身的利益最大化为目标进行价格重复博弈。本文在建立了动态系统模型的基础上，分析了模型均衡点的稳定性，并利用Matlab进行数值模拟，运用分岔图、最大Lyapunov指数以及混沌吸引子来综合判定了系统的复杂动力特征，并分析了稳定及混沌系统对于决策变量初值的敏感性，最后进行了混沌控制。得到结论：1)制造商和零售商对各自决策变量的调节速度过快时，会使得系统陷入一种混沌无序的状态，当系统陷入混沌时，制造商和零售商的价格和利润将会很难进行预测，企业便难以获得稳定的利润以可靠地满足市场的需求。2)当系统处于稳定状态时，决策主体对于决策变量初值的微小改变所导致的偏差会随着迭代次数的增加而逐渐变为0，而当系统处于混沌状态时，决策主体对于决策变量初值的微小偏差会随着迭代次数的增加而逐渐增大几十或几百倍，即系统具有很强烈的初值敏感性。3)制造商应与零售商联合起来，对市场进行一定的混沌控制，当加入调节参数进行混沌控制时，可将系统混沌状态有效地延迟或消失。

[1] Liang Y J,Pokharel S, Lim G H.Pricing used products for remanufacturing[J]. European Journal of Operational Research, 2009(193): 390-395.

[2]Chen J M, Chang C I. The co-opetitive strategy of a closed-loop supplychain with remanufacturing[J]. Transportation Research Part E, 2012(48): 387-400.

[3]Maiti T, Giri B C. A closed loop supply chain under retail price and product quality dependent demand[J]. Journal of Manufacturing Systems, 2015, 37: 624-637.

[4]He Y. Acquisition pricing and remanufacturing decisions in a closed-loop supply chain[J]. International Journal of Production Economics, 2015, 163: 48-60.

[5]肖迪, 黄培清.基于产品时间价值的闭环供应链库存策略研究[J].管理工程学报, 2008, 22(4): 146-148. Xiao Di, Huang Peiqing. A study on inventory policy of closed loop supply chain based on time value of products[J]. Journal of Industrial Engineering, 2008, 22(4): 146-148.

[6]聂佳佳.零售商信息分享对闭环供应链回收模式的影响[J]. 管理科学学报, 2013, 16(5): 69-82. Nie Jiajia. Effects of retailer information sharing on collecting modes of closed-loop supply chain[J]. Journal of Management Sciences in China, 2013, 16(5): 69-82.

[7]Savaskan R C, Van Wassenhove L N.Reverse channel design:the case of competing retailers[J]. Management Science, 2006,52 (1):1-14.

[8]Zu J M, Zhang N, Dai Y, et al. Managing channel profits of different cooperative models in closed-loop supply chains[J]. Omega, 2016, 59: 251-262.

[9]Huang M, Song M, Lee L H, et al. Analysis for strategy of closed-loop supply chain with dual recycling channel[J]. International Journal of Production Economics, 2013, 144(2): 510-520.

[10] 肖雪珣, 陈晓荣.基于博弈论的闭环路供应链回收策略[J]. 科学技术与工程, 2011,11(6) :1277-1283. Xiao Xuexun, Chen Xiaorong. Study on closedloop supply chain tack-back strategy based on game theory[J]. Science Technology and Engineering, 2011,11(6) :1277-1283.

[11] 徐兵.双营销渠道闭环供应链决策模型与协调[J].西南交通大学学报, 2012,47(6):042-1046. Xu Bing, Wu Ming. Product remanufacturing and pricing decisions and supply chain coordination of closed-loop supply chain with dual sale channels[J]. Journal of Southwest Jiaotong University, 2012,47(6):042-1046.

[12] Bischi G I, Kopel M. Equilibrium selection in a nonlinear duopoly game with adaptive expectations[J]. Journal of Economic Behavior & Organization, 2001, 46(1): 73-100.

[13] Akio M, Yasuo N. Statistical dynamics in a chaotic cournot model with complementary goods[J]. Journal of Economic Behavior & Organization, 2006, 61: 769-783.

[14] Elsadany A A. Dynamics of a delayed duopoly game with bounded rationality[J]. Mathematical and Computer Modeling, 2010, 52(9/10): 1479-1489.

[15] 郭悦红, 马军海, 王冠辉.回收再制造系统的重复博弈模型及复杂性分析[J]. 工业工程, 2011, 14(5): 66-70. GuoYuehong, Ma Junhai, Wang Guanhui. Modeling and analysis of recycling and remanufacturing systems by using repeated game model[J]. Industrial Engineering Journal, 2011, 14(5): 66-70.

[16] 谢磊, 马军海. 中国废旧家电回收市场稳定性及其应用研究[J]. 复杂系统与复杂性科学, 2015, 12(3): 96-109. Xie Lei, Ma Junhai. The stability and application analysis on the home appliance recycling market in China[J]. Complex Systems and Complexity Science, 2015, 12(3): 96-109.

(责任编辑 李进)

Complexity of Evolutionary Gameand Control in a Closed-Loop Supply Chain with Dual-Channel Recycling

YU Miao, MA Junhai

(College of Management and Economics, Tianjin University, Tianjin 300072)

This paper builds models of one manufacturer and one retailer recycle the waste products at the same time, to analyze market operation system when different prices settings between new products and remanufactured products. Using game theory, chaotic dynamics theory and complexity dynamics theory, we perform the theory verification and reality simulation through numerical calculation.Results show that a fast speed of price adjustment of the manufacturer or the retailer will both lead the system into chaos via period-doubling bifurcations. Focusing on the harmful effects of chaotic system, adjustment parameter can be used to control the chaos efficiently. This research whose results have a strong reference value to practical problems, has a great value both of theory and application.

closed-loop supply chain; mixed recycling channels; evolutionary game; chaos

1672-3813(2017)02-0065-10；

10.13306/j.1672-3813.2017.02.010

2016-05-10；

2016-11-27

国家自然科学基金(71571131)；教育部博士点基金(20130032110073)

于淼(1992-)，女，黑龙江哈尔滨人，硕士研究生，主要研究方向为闭环供应链定价。

O29

A