基于空间活跃度网络的搜索策略研究

韩定定，柳 康，陈 超，陈 趣

(华东师范大学上海市多维度信息处理重点实验室,上海 200241)

基于空间活跃度网络的搜索策略研究

韩定定，柳 康，陈 超，陈 趣

(华东师范大学上海市多维度信息处理重点实验室,上海 200241)

基于具有时变特性与空间特性的空间活跃度网络模型，研究了时变网络中的搜索问题。结合空间活跃度网络的特性，引入了搜索时间、搜索路径长度和等待时间3种搜索策略的评价指标，提出了最大活跃度搜索策略、改进的贪婪搜索策略和最大活跃度最小距离搜索策略。利用这些策略在空间活跃度网络中进行搜索，研究发现和其他的搜索策略相比，改进的贪婪搜索策略与最大活跃度最小距离搜索策略具有较好的搜索性能，能够很好地适用于这种类型的时变网络，从而优化了目标搜索的过程。

时变网络；活跃度驱动；空间性；搜索策略；最优搜索

0 引言

在复杂网络的研究中，研究对象通常是静态网络[1-3]，即网络的拓扑是固定不变的。然而，现实网络总是随着时间不断变化，网络内的节点与连边会不断产生或消失[4]。例如，因特网中的网页链接每天都在不断增加和减少；在通信网络中，用户间的连接会受通信状态影响持续不同时间等。这些现象均体现了网络的时变特征，我们把具有时变特征的网络统称为时变网络。通过对时变网络的拓扑变化情况与动力学过程进行探索，可以帮助人们更好地理解真实网络的结构与功能，从而解决现实生活中的诸多问题。

时变网络的研究主要包括：时变数据的描述与处理[5-7]、时变拓扑统计特性的定义[8-10]、时变条件下的社团探测与演化规律研究[11]以及真实系统的时变特性建模等[12-14]。在时变网络建模研究中，学者们建立了很多不同的时变网络模型，其中较为著名的是Nicola Perra等人提出的活跃度驱动模型[15]。在一些受人类行为影响的网络中，个体的行为存在着很大差异，NicolaPerra等人将这些行为差异定义为个体的活跃度，并从个体活跃度驱动的角度提出了一种时变网络的建模方法，构建了活跃度驱动模型，为人们理解时变网络提供了新的视角。该模型指出，使网络产生时变特性的内在驱动力是节点的活跃度。然而在复杂的现实网络中，除了活跃度外还存在很多其它的特性，比如空间性、聚集性等，它们也影响着网络的结构特征。

搜索是复杂网络中基础的动力学过程之一。搜索问题起源于20世纪60年代Milgram做的信件传递实验，他利用该实验来估计社会网络中两个人之间的实际距离，通过实验结果提出了著名的“六度分离”推断[16]。Milgram的实验揭示了社会网络的两个性质，一是网络的小世界特性，二是网络的可搜索特性。网络的可搜索特性其实与网络本身的结构性质密切相关。除了网络结构对搜索过程的影响，搜索策略也是影响网络搜索能力的重要因素。现有的复杂网络搜索策略的研究多是基于网络拓扑不变的条件，研究的载体网络主要是一系列静态网络，缺乏针对时变网络的研究。网络的时变特征使得网络结构随着时间动态变化，而不同的拓扑结构亦会对网络上的动力学过程产生重大影响。

以疾病或病毒在网络上的传播为例，当网络的拓扑结构发生变化时，病毒在网络上的传播路径会受到影响，从而使疾病传染强度的阈值也相应发生变化，呈现或上升或下降的趋势，进而影响疾病的传播速度与传播范围。对于具有时变特征的实际网络，之前的一些搜索策略可能无法使搜索效率达到最优，策略的有效性也没有得到验证。比如在搜索到某个点时所有与该点的连边都消失了，该点成为了孤立的节点，无法将该点上的信息传递出去，这就会使得搜索失败。因此研究时变网络上提高搜索效率的策略，探索时变拓扑的特殊网络特性，挖掘时变网络动力学特征具有必然性。

本文基于具有时变性和空间性的空间活跃度网络模型对时变网络进行搜索研究，旨在验证静态网络搜索策略的有效性，并设计符合该时变网络特性的搜索策略，系统地研究时变网络中的搜索问题。

1 空间活跃度网络模型构建

本文提出一种空间活跃度网络模型，主要考虑了两方面的内容：一是节点的活跃度，二是节点的地理位置。活跃度特性使得网络具有时变的特征，地理位置特性使得生成的连边具有地理趋近性。模型设定N个节点分布在L×L的二维网格上，使得每个节点都具有坐标信息，其中N=L×L。每个节点i赋予活跃度，ai代表了在单位时间内给定的节点能自发与其他节点生成连边的概率。ai满足幂律分布F(a)，即F(a)∝a-γ，γ为活跃度幂指数，网络的生成机制如下：

1)在每个时间步长t内，二维网格内节点之间均无连边；

2)节点i根据概率aiΔt变成活跃节点，与其他m个节点产生m条连边，其中与节点j连接的概率满足：

(1)

其中，rij为节点i与节点j之间的曼哈顿距离。α为偏好连接幂指数，当指数α取值为0时，节点在选择连边时不具地理偏好性，能与任意的其他节点都产生连边。随着幂指数α值的增加，两个曼哈顿距离较远的节点之间有连边的概率会越来越小；

3)在t+Δt时刻，网络中所有生成的连边同时消失，然后重复第2)步的过程形成下一个时刻的拓扑结构。

为了直观地说明偏好连接指数α对网络特性的影响，画出了α取不同值时整个网络聚合拓扑的对比，如图1所示。设定节点数N=L×L=625，聚合时间窗t=5。拓扑图通过复杂网络可视化软件工具Gephi画出，为了清晰地显示网络的拓扑结构，省略了网络中孤立的节点。在图1a中，设置α=0，此时连边分布随机，可以看出图中的长边数与短边数基本差不多。在图1b中，设置α=3，节点在连边时具有空间上的偏好连接特性，更易与距离自己近的节点产生连边，而与距离远的节点产生连边的概率很小，因此在图中表现为短边数比长边数多，体现了局部的聚集现象。

2 空间活跃度网络搜索策略研究

在构建了空间活跃度网络模型，对网络结构特性有了一定认识后，希望研究该网络模型上的搜索过程从而能够应用到实际生活中。对于搜索而言，如何在给定的网络结构中快速搜索到目标是人们希望解决的问题，这就涉及到搜索策略的研究。通过选取和设计合适的搜索策略，以较小的搜索代价快速准确地搜索到目标并进行反馈，这具有重要的现实意义。而搜索策略的制定需要通过网络的局部信息，诸如节点的度或者介数等一系列刻画网络特征的参数。那么，根据上一章节中我们构建的空间活跃度网络模型特性，我们是否可以利用节点的活跃度和地理空间信息来设计出合理的搜索策略以适应该时变网络的特点？

图1 不同偏好连接指数下网络的拓扑结构Fig.1 The topology of the network under different preferences link index

2.1 搜索效率的衡量指标

搜索策略需要具体的测量参数作为评价指标，用来比较各种搜索策略的优劣。这一部分主要介绍了3种衡量搜索策略性能的参数，它们分别是搜索步数、搜索路径长度以及等待时间，分别从不同的角度表示了搜索策略在实际网络搜索中的效率与开销。

2.1.1 搜索时间

搜索时间是指，从源节点开始至查找到目标节点结束这个过程中所经历的时间间隔，即在网络搜索过程中找到明确目标节点的搜索步数。对复杂网络的搜索来说，搜索时间是重要的衡量参数，它最直接反映了搜索策略的速度。通常来说，搜索时间越短，相应的搜索策略的效率就越高，搜索速度就越快。因此好的搜索策略的搜索时间一般都很短。而在一般的大规模网络中，光靠几条搜索出来的路径对应的搜索时间是不够有说服力的，所以一般采取平均搜索时间这个统计性质来衡量搜索速度，在文章中用T表示。为了便于计算，在接下来搜索策略的研究中设定时变网络中拓扑变化的时间间隔与每一步搜索的时间间隔在相同的时间尺度内。也就是说，每进行一步搜索，网络的拓扑就会发生一次变化。因此，搜索时间也指从源节点开始至搜索到目标节点期间网络拓扑的演化时间。

2.1.2 搜索路径长度

在空间活跃度网络中，所有的节点都分布在二维网格上，具有各自的地理空间信息，节点间的距离又称为曼哈顿距离，可通过节点坐标计算得到。假设节点u的坐标为(i,j)，节点v的坐标为(k,l)，则两点间的曼哈顿距离d(u,v)为

d(u,v)=d((i,j),(k,l))=|k-i|+|l-j|

(2)

搜索路径长度定义为从源节点开始搜索到目标节点时所走过的曼哈顿距离之和。对于起点为x0，终点为xn，搜索时依次经过节点x1，x2，…，xn-1的搜索路径长度用公式表示为

(3)

在现实网络中，搜索路径长度一般映射为搜索的成本大小。比如在航空网络中，从一个城市飞到另一个城市所需要花费的成本可考虑成这一趟航班的票价，而票价主要受航程距离的影响，长距离的航班票价往往比短距离的航班票价贵。因此，搜索成本可以用搜索路径长度来表示。和搜索时间一样，计算几次搜索结果的搜索路径长度是不够的，所以我们一般在多次搜索后计算平均搜索路径长度这一统计特性，在文章中用S表示，它也是衡量搜索策略好坏的重要指标。

2.1.3 等待时间

由于空间活跃度网络的拓扑具有时变特性，所以在进行搜索时，会遇到信息在上一时刻传递到当前节点，而当前节点在当前时刻没有与任何其他节点发生连边的情况。这时该节点成了孤立的节点，没有邻居节点使其能将信息传递出去。为了避免搜索的失败，引入等待时间这一指标，用W表示，在搜索过程中遇到上述状况时对等待时间进行累加，直到在某一时刻拓扑的变化使得该节点重新有了邻居节点，从而能够重新将信息传递出去，保证搜索过程的顺利进行。因此，在搜索开始时将等待时间初始化为0，在搜索过程中每次遇到上述状况时，将其值加1，直到搜索过程的完成。由搜索时间的定义可知，在搜索时间中包含了等待时间，通过计算搜索时间与等待时间可以知道在搜索过程中真正发生信息传递的步数。

2.2 搜索策略的设计

网络搜索过程开始时，首先选定源节点和目标节点，然后从源节点开始，在搜索到当前节点时，利用不同的搜索策略所制定的规则，选择出符合条件的节点作为下一步传递信息的节点，并计算相应的搜索效率指标。以此循环，直至搜索到目标节点，完成整个搜索过程，通过搜索指标比较各搜索策略的性能差异。

常用的搜索策略有随机游走搜索策略[17]、最大度搜索策略[18-19]和贪婪搜索策略[20]等。在选择下一步的信息传递节点时，随机游走策略选取的是一个随机的邻居节点，最大度策略选取的是度最大的邻居节点，贪婪策略选取的是距目标节点最近的邻居节点。这些搜索策略适用于静态网络，在时变网络中的有效性还有待验证。

2.2.1 最大活跃度搜索策略

在空间活跃度网络中，影响网络拓扑的主要因素是节点的活跃度属性与地理空间偏好连接属性。一方面，活跃度越大的节点在每个时间间隔内具有越大的概率成为活跃节点，从而拥有较多的邻居节点。另一方面，活跃节点越容易与距离近的节点产生连边。因此，在进行网络搜索时，理论上通过这些活跃度大的节点搜索到目标节点的概率也会越大。因此，我们提出一种与最大度搜索策略类似的最大活跃度搜索策略，该搜索策略在搜索的每一步把信息传递给活跃度最大的邻居节点，这些节点产生连边的能力较强，从而使得找到目标节点的概率增大。最大活跃度搜索策略的具体搜索过程如下：

1)随机选择网络中的源节点s与目标节点t，并将s赋值给s0，s0为当前节点。

2)搜索节点s0的邻居节点，判断其中是否存在目标节点t，如果存在，则搜索结束，否则执行第3)步。

3)找到s0的邻居中活跃度最大的节点sn，将搜索信息传递给sn，并将sn赋值给节点s0。

4)重复执行第2)和第3)步，直至搜索到目标节点t为止。

2.2.2 改进的贪婪搜索策略

我们对贪婪搜索策略进行改进，除了计算当前节点的邻居节点到目标节点的距离di外，另外也将当前节点到目标节点的距离d0计算在内，选择其中最小的值对应的节点作为下一跳的地址，若d0比任何的di都小，则在当前时刻不进行信息的传递，而是停留在当前节点上等待下一时刻拓扑的变化。这样做可以保证每次信息传递到的节点都会离目标节点的距离更近，从而避免传递时方向的偏离产生更多的搜索成本，但是这样做可能会使在每一时刻发生信息传递的概率变小，进而使得等待时间增加。搜索过程如下：

1)随机选择网络中的源节点s与目标节点t，并将s赋值给s0，s0为当前节点。

2)搜索节点s0的邻居节点，判断其中是否存在目标节点t，如果存在，则搜索结束，否则执行第3)步。

3)计算s0到目标节点的距离d0以及它的邻居节点各自到目标节点的距离di，若d0比任何di都小，则不进行信息的传递，停留一个时间间隔；若di中有比d0小的邻居节点存在，则找到其中di最小的邻居节点i，将搜索信息传递给i，并将i赋值给节点s0。

4)重复执行第2)步和第3)步，直至搜索到目标节点t为止。

2.2.3 最大活跃度最小距离搜索策略

在搜索的过程中，当前节点在选择下一跳节点时，使用贪婪搜索策略，可以做到不使传递信息的方向偏离我们所要搜索的目标节点；使用最大活跃度搜索策略，将搜索信息传递给具有较大活跃度的节点，而这些节点往往拥有较多的长程连边，使得搜索到目标节点的可能性增大。因此，可以结合最大活跃度搜索策略和贪婪搜索策略的优点，每次在传递时将信息传递给活跃度较大且离目标节点较近的邻居节点，从而快速准确地找到目标节点。利用交通意识路由协议(Traffic Awareness Protocol, TAP)的设计思想[21]，引入耦合函数

J(i)=c/ai+(1-c)di

(4)

该搜索策略在传递信息的每一步将信息传递给J(i)最小的邻居节点，其中ai为节点i的活跃度，di为节点i到目标节点的距离，c为耦合系数，0≤c≤1。当c=0时，此策略为贪婪搜索策略；当c=1时，此策略为最大活跃度搜索策略；当c取其它值时，在选择最佳路径时会同时考虑活跃度的因素和路径长度的因素。搜索过程如下：

1)随机选择网络中的源节点s与目标节点t，并将s赋值给s0，s0为当前节点。

2)搜索节点s0的邻居节点，判断其中是否存在目标节点t，如果存在，则搜索结束，否则执行第3)步。

3)计算各邻居节点的J(i)值，找到其中最小的值对应的邻居节点i，将搜索信息传递给i，并将i赋值给节点s0。

4)重复执行第2)步和第3)步，直至搜索到目标节点t为止。

3 搜索策略的比较

建立一组不同规模的空间活跃度网络，设定偏好连接幂指数α=2，连边数m=6，活跃度幂指数γ=2.8，耦合系数c=0.01，随机地选取5 000对节点作为源节点和目标节点，分别利用随机游走搜索策略(RW)、最大活跃度搜索策略(MA)、贪婪搜索策略(GY)、改进的贪婪搜索策略(IMGY)和最大活跃度最小距离搜索策略(MAMD)进行网络搜索。为了衡量不同搜索策略的搜索效率，我们分别计算各搜索策略的平均搜索时间、平局搜索路径长度和平均等待时间。3种指标越小，那么表示对应的搜索策略的效率就越高。

图2为不同搜索策略下网络规模与平均搜索时间的关系。由图中曲线关系可得，随着网络规模的增大，所有搜索策略的平均搜索时间都变长了。和其他的几种搜索策略相比，改进的贪婪搜索和最大活跃度最小距离搜索策略都具有明显的优势，能够大大缩短平均搜索时间，且最大活跃度最小距离搜索策略的平均搜索时间比改进的贪婪搜索策略的平均搜索时间还短。这是因为虽然在搜索过程的每一步都使信息的传递方向更靠近目标节点，但是选择一个活跃度较大的邻居节点，即使该邻居离目标节点很远，但是该邻居节点在下一时刻活跃并且产生长程连边的概率很大，那么在下一次传递信息时，可以把信息沿着该长程连边传递，从而使接受信息的节点有可能离目标节点更近。最大活跃度最小距离搜索策略在搜索的过程中同时考虑了节点的活跃度与节点离目标节点的距离这两个因素，仿真结果也证明了该策略的平均搜索时间比其他搜索策略的平均搜索时间更短。

在平均搜索路径长度方面，改进的贪婪搜索策略和最大活跃度最小距离搜索策略也表现了较好的性能，且改进的贪婪搜索策略的平均搜索路径比最大活跃度最小距离搜索策略更短，如图3所示。这是由于改进的贪婪搜索策略保证了在进行每一步的信息传递时都会离目标节点更近，在出现邻居节点到目标节点的距离均比当前节点到目标节点的距离长这种情况时，不进行信息的传递而是等待一个时间间隔，从而避免了传递时方向的偏移，减少了多余的搜索路径，获得较短的平均搜索路径长度。

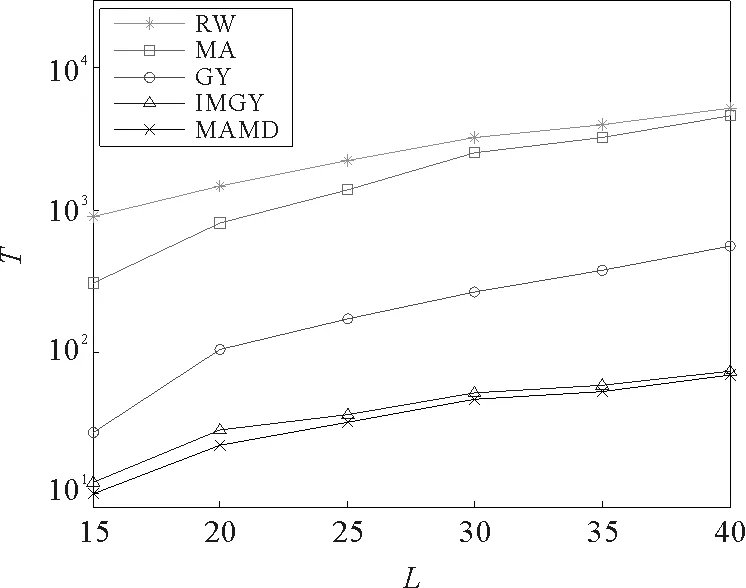
图2 网络规模L与平均搜索时间T的关系Fig.2 The relationship of network size L and the average search time T

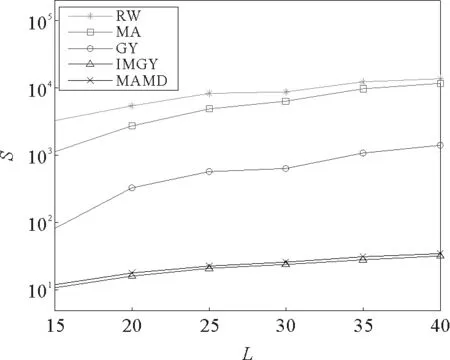
图3 网络规模L与平均搜索路径长度S的关系Fig.3 The relationship of network size L and average search path length S

在平均等待时间方面，由图4中曲线可知改进的贪婪搜索与最大活跃度最小距离搜索策略所用的平均等待时间依然比其他的搜索策略短很多。例如在网络规模N=L×L=400时，改进的贪婪搜索与最大活跃度最小距离搜索策略的平均等待时间分别只有23和20，而贪婪搜索策略的则为42，其他的搜索策略更高。尽管网络的拓扑随着时间在不断发生变化，这两种搜索策略还是能够较快地将搜索信息传递出去。

图5为各搜索策略的平均等待时间与平均搜索时间的比值。可以发现，改进的贪婪搜索策略与最大活跃度最小距离搜索策略的等待时间占据了平均搜索时间的很大一部分。比如在网络规模N=L×L=400时，改进的贪婪搜索策略为82%，最大活跃度最小距离搜索策略为91%，而其他搜索策略均在41%以下。这说明在搜索过程中，运用这两种搜索策略时真正用于信息传递的搜索步数并不多。既便如此，这两种策略的搜索效率比其它的搜索策略效率还是高很多。这是因为改进的贪婪搜索策略保证了网络搜索时方向不会偏离目标节点，最大活跃度最小距离搜索策略则同时考虑了节点的最大活跃度和距目标节点的最小距离，从而大大提高了搜索效率。而其他的几种搜索策略虽然也能搜索到目标节点，但是由于搜索方向的偏移性产生了很多曲折迂回的搜索路线，以及低活跃性的节点在很长的时间间隔内无法产生连边将信息传递出去，这都导致了平均搜索时间和平均搜索路径长度的增加。

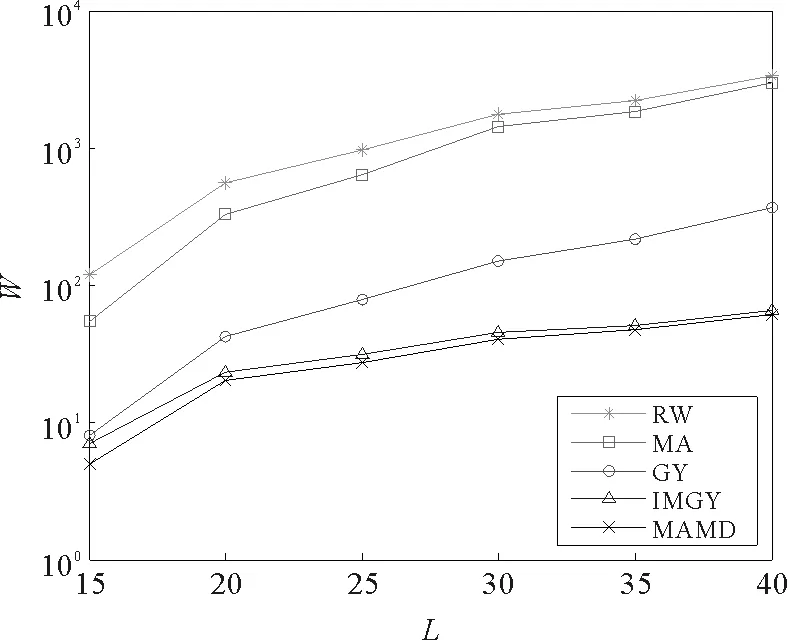
图4 网络规模L与平均等待时间W的关系Fig.4 The relationship of network size L and the average waiting time W

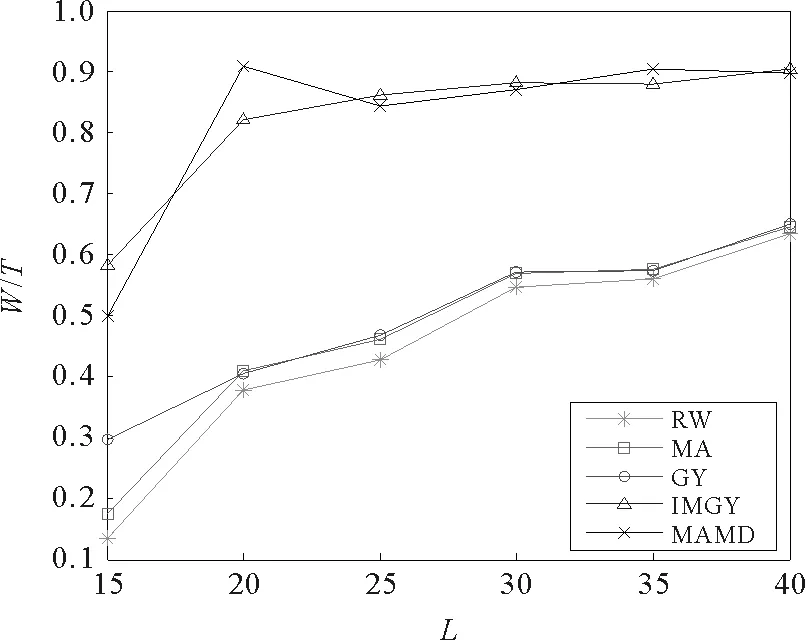
图5 不同网络规模L下等待时间与搜索时间比值W/TFig.5 The waiting time and the search time ratio W/Tunder different network size L

综上所述，在空间活跃度网络上进行搜索工作时，结合网络的时变性与空间性特点，利用最大活跃度最小距离搜索策略和改进的贪婪搜索策略均能较快搜索到目标，在很大程度上提高了搜索的性能。将本文提出的搜索策略应用于现实社交网络中，用户在每次搜索时将信息传递给与自己距离近且在社交活动中表现活跃的用户，则会加快搜寻的速度，从而大大提升目标搜索的效率。因此，这些搜索策略的研究工作也为现实网络中的搜索问题提供了重要的理论指导。

4 结语

本文构建了一种具有时变特性与地理空间特性的空间活跃度网络模型，在该网络上进行搜索策略的研究。首先引入了搜索时间、搜索路径长度和等待时间3个衡量搜索效率的指标；其次结合空间活跃度网络的特性依次提出了最大活跃度搜索策略、改进的贪婪搜索策略和最大活跃度最小距离搜索策略；最后利用这些策略进行网络搜索，通过比较发现改进的贪婪搜索策略与最大活跃度最小距离搜索策略能较好地适应空间活跃度网络的特点，表现出较好的搜索性能。本文的研究工作为现实网络中一些搜索问题的解决提供了思路与方法。

[1]Watts D J, Strogatz S H. Collective dynamics of “small-world” networks[J]. Nature, 1998, 393(6684):440-442.

[2]Liljeros F, Edling C R, Lan A. The web of human sexual contacts[J]. Nature, 2001, 411(6840):907-908.

[3]Ebel H, Mielsch L I, Bornholdt S. Scale-free topology of e-mail networks[J]. Physical Review E, 2002, 66(3):035103.

[4]Holme P, Saramäki J. Temporal networks[J]. Physics Reports, 2012, 519(3):97-125.

[5]Bearman P S, Moody J, Stovel K. Chains of affection: the structure of adolescent romantic and sexual networks[J]. American journal of sociology, 2004, 110(1): 44-91.

[6]Cheng E, Grossman J W, Lipman M J. Time-stamped graphs and their associated influence digraphs[J]. Discrete Applied Mathematics, 2003, 128(2): 317-335.

[7]Riolo C S, Koopman J S, Chick S E. Methods and measures for the description of epidemiologic contact networks[J]. Journal of Urban Health, 2001, 78(3): 446-457.

[8]Pan R K, Saramäki J. Path lengths, correlations, and centrality in temporal networks[J]. Physical Review E, 2011, 84(1): 016105.

[9]Tang J, Musolesi M, Mascolo C, et al. Temporal distance metrics for social network analysis[C]. Proceedings of the 2nd ACM Workshop on Online Social Networks. ACM, 2009: 31-36.

[10] Xuan B B, Ferreira A, Jarry A. Computing shortest, fastest, and foremost journeys in dynamic networks[J]. International Journal of Foundations of Computer Science, 2003, 14(2): 267-285.

[11] Holme P, Edling C R, Liljeros F. Structure and time evolution of an Internet dating community[J]. Social Networks, 2004, 26(2):155-174.

[12] Medo M, Cimini G, Gualdi S. Temporal effects in the growth of networks[J]. Physical review letters, 2011, 107(23): 238701.

[13] Chen Q, Han D D, Qian J H, et al. Optimal temporal path on spatial decaying networks[J]. Journal of Applied Analysis and Computation, 2016, 6(1):30-37.

[14] Chen Q, Qian J H, Zhu L, et al. Optimal transport in time-varying small-world networks[J]. Physical Review E, 2016, 93(3): 032321.

[15] Perra N, Gonçalves B, Pastor-Satorras R, et al. Activity driven modeling of time varying networks[J]. Scientific Reports, 2012, 2(6):1717-1720.

[16] Milgram S. The small world problem[J]. Psychology Today, 1967, 2(1):185-195.

[17] Pandit S A, Amritkar R E. Random spread on the family of small-world networks[J]. Physical Review E, 2001, 63(4): 041104.

[18] Adamic L A, Lukose R M, Huberman B A. Local search in unstructured networks[J]. Handbook of Graphs & Networks, 2002:295-317.

[19] Adamic L A, Lukose R M, Puniyani A R, et al. Search in power-law networks[J]. Physical review E, 2001, 64(4): 046135.

[20] Kleinberg J M. Navigation in a small world[J]. Nature, 2000, 41(10):2496-2515.

(责任编辑 耿金花)

Search Strategies Based on Spatial Activity Network

HAN Dingding, LIU Kang, CHEN Chao, CHEN Qu

(Shanghai Key Laboratory of Multidimensional Information Processing, East China Normal University, Shanghai 200241, China)

Based on spatial activity network with the characteristics oftime varying and spatial property, searching on time varying network was studied in this paper. Combined with the characteristics of spatial activity network, search time, search path length and waiting time were introduced as evaluation indexes for search strategy. And maximum activity searching strategy, improved greedy searching strategy and maximum activity minimum distance searching strategy were proposed. It was found that using improved greedy searching strategy and maximum activity minimum distance searching strategy to search on the spatial activity network would get higher efficiency than any of other strategies. They were suitable for this type of time varying network and able to optimize the searching process.

time varying network; activity driven; spatial property; searching strategies; optimal searching

1672-3813(2017)02-0103-07；

10.13306/j.1672-3813.2017.02.015

2016-11-01；

2016-12-28

韩定定(1968-)，女，上海人，博士，教授，主要研究方向为复杂网络与智能信息处理。

TP393.2

A