基于全局K-means算法的超像素分割方法
2017-07-18吉长东李相泽敖国政辽宁工程技术大学测绘与地理科学学院辽宁阜新505东北大学计算机科学与工程学院辽宁沈阳089辽宁工业大学电子与信息工程学院辽宁锦州00
吉长东, 李相泽, 敖国政(. 辽宁工程技术大学 测绘与地理科学学院, 辽宁 阜新 505;. 东北大学 计算机科学与工程学院, 辽宁 沈阳 089;. 辽宁工业大学 电子与信息工程学院, 辽宁 锦州 00)
基于全局K-means算法的超像素分割方法
吉长东1, 李相泽2, 敖国政3
(1. 辽宁工程技术大学 测绘与地理科学学院, 辽宁 阜新 125105;2. 东北大学 计算机科学与工程学院, 辽宁 沈阳 110819;3. 辽宁工业大学 电子与信息工程学院, 辽宁 锦州 121001)
为了提高超像素分割的性能,提出了一种基于全局K-means算法的超像素分割方法。该算法利用全局K-means算法计算超像素聚类,优化了超像素的分割质量,并根据聚类后的超像素结果从图像中分割出目标.实验数据来自于国际公认的PASCAL VOC 2007数据集.实验结果表明,与Wang算法和ISLIC算法相比,提出的分割算法的PRI、CR、VOI及运行时间4个指标分别平均提高9.38%、17.13%、21.67%、10.50%,可以实现更佳的图像分割效果.
图像分割; 超像素; 全局K-means算法; 聚类
图像分割是图像处理中的重要部分,良好的分割算法能够对目标提取和识别提供巨大帮助.为了提高分割算法的性能,加州大学的X.Ren和J.Malik提出了一种符合人类视觉感知的自然图像分割算法,即超像素(Superpixel)[1].近几年,在计算机视觉方面,超像素已经受到了广泛的重视[2-3].与普通的像素相比,超像素有4个优势:①计算复杂度低;②符合人眼特点;③图像信息描述效率高;④图像信息保存完整.虽然超像素具有许多良好的属性,但是这些属性的发挥都是基于高质量的超像素.所以,如何分割出超像素就成为关键问题.目前,对于超像素分割已经提出了许多有效的改进算法.Liu等人[4]提出了基于熵率的ERS(entropy rate superpixel segmentation)算法,该算法通过构造新的目标函数,直接控制生成的超像素数量,获得的超像素边缘贴合度较好;Zhang等人[5]提出了基于伪布尔函数(pseudo-boolean function)的超像素分割算法,其基本思想是将图像从垂直和水平两个方向用半重叠的图像带(strip)覆盖,使任意像素只属于其中一个图像带;Bergh 等人[6]提出了SEEDS算法,该算法从一个规则图像网格出发,渐进地修正超像素边缘的像素点,最终获得分割结果;Wang等人[7]提出了结构敏感的超像素分割算法,该算法利用测地线距离代替欧氏距离度量像素间相似性,用于衡量图像局部结构密度.该算法能够根据图像结构密度自适应地调整超像素分布疏密程度,同时保持了较高的计算效率.
本文基于全局K-means算法来分割超像素,该算法是传统K-means算法的一种有效改进.通过实验证明,该算法获得的超像素能够有效地对静态图像中的目标进行提取.
1 K-means算法
K-means算法是一种聚类算法,不同的学者在不同的领域分别独立提出了这种聚类思想[8].虽然K-means算法提出至今已经有半个世纪,但依然是应用最广泛的聚类算法之一.
1.1K-means算法特点
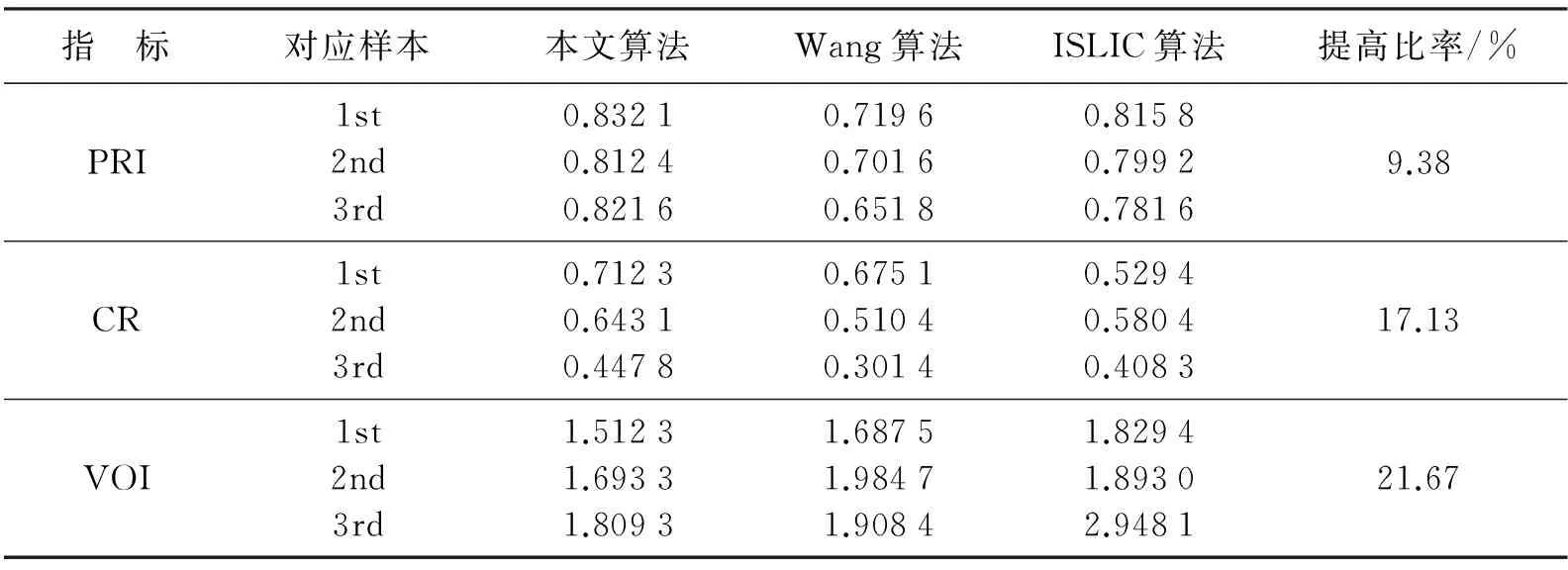
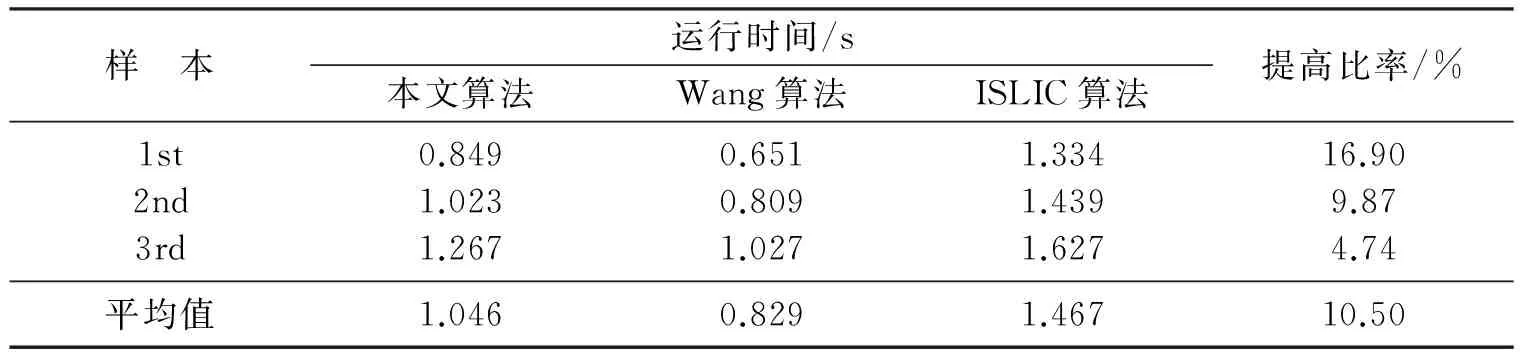
K-means算法能对大型数据集进行高效分类,其计算复杂性为O(tKmn).其中,t为迭代次数,K为聚类数,m为特征属性数,n为待分类的对象数,通常m 但K-means算法存在着如下四个主要缺点:①分群结果与初始点的选取有关,分群的结果不稳定甚至错误;②对于球形群的聚类效果会很好,但却无法适用于任意形状的群;③对离群与噪声目标较为敏感;④只适用于数值型数据,对于分类型数据则难以进行处理. 此外,K-means算法在目标分群的应用上也具有一定的局限性.通常,目标会用很多个属性特征来描述,而对于目标分群而言,有些属性很重要,但有些属性特征甚至不会影响到目标对象的聚类[8].有很多传统的基于距离的聚类方法应用到目标的复杂多维属性特征上获得的效果很不理想.主要原因是传统K-means类的算法所采用的度量准则是单纯的欧氏距离的度量方法,也就是计算每个样本数据到每个聚类中心的欧氏距离,最后将数据划入距离最近的类中.由于该方法没有区分每个属性对于聚类的重要程度,在进行多维复杂数据聚类时,传统K-means算法的效果很不理想. 1.2K-means算法流程 K-means算法应用于目标分群的主要流程: 输入:群的数目k;包含n个目标实体的数据库. 输出:k个群. 步骤如下: (1) 初始化,随机指定k个聚类中心(c1,c2,…,ck); (2) 分配xi,对每一个样本xi,找到离它最近的聚类中心cv,并将其分配到cw所标明的类; (3) 修正cw,将每一个cw移动到其标明的类的中心; (5) 判断D是否收敛,如果D值收敛,则return(c1,c2,…,ck)并终止本算法;否则,返回步骤(2). 与普通像素点相比,利用超像素描述图像信息能够获得更高的效率.因为超像素划分之后,会以此为单位对图像的各项特征进行统计,这样可以高效描述图像信息,由此对后续的图像处理都有很大帮助.超像素的形成是根据相似特征得到的,属于聚类问题,所以本文使用全局K-means算法来获取超像素. 2.1 全局K-means算法 K-means算法在进行超像素分割的过程中,主要的问题就是由于其聚类结果严重依赖于初始聚类中心的选取,最终聚类结果非常不稳定,从而对每次得到的超像素影响很大.为了解决对初始位置敏感这一瓶颈问题,A.Likas等人提出了一种确定性的全局优化算法即GlobalK-means(GKM)算法,该方法初始点的选取不依赖于任何初始参数值,在其局部搜索上使用K-means算法[9-10].与大部分全局聚类算法不同的是,GKM算法采用一种增量的方式,即每循环一次只增加一个新的聚类中心而不是随机地选取所有初始聚类中心.由此可见,该算法对于超像素分割非常适用. GKM算法的基本框架如下: 输入:聚类数K,数据Xij,1≤i≤N,1≤j≤D; 输出:最终聚类中心(z1,…,zk),聚类错误F. 步骤如下: (1) 初始化k=1,z1=mean(X); (2) 利用K-means算法求出第k+1类的初始最优类中心; (3) 利用K-means算法优化得到的前k+1类聚类中心(z1,…,zk,zk+1); (4) 如果k+1>K,算法结束,否则返回步骤(2),并且k=k+1. GKM算法首先解决仅聚为一类(k=1)的问题,此时最优的聚类中心位于所有数据的质心位置,即z1=mean(X).当本文已经求出了k(k>1)类问题的结果之后,就通过以下方式求解k+1类聚类问题:(z1,…,zk)表示已经求出的k类问题的最优解,设置初始位置为(z1,…,zk,xi)(i=1,2,…,N)执行N次K-means算法得出的最优结果所对应的聚类中心就是k+1类聚类问题的初始最优解.然后执行K-means算法优化初始解(z1,…,zk,zk+1)直到结果不再改善为止[11-12]. GKM算法通过一个确定有效的全局搜索来最小化聚类错误函数,故其性能因为不受聚类中心初始位置的影响而非常稳定.GKM算法较K-means算法是相当具有优势的. 2.2 超像素分割 在利用GKM算法进行超像素分割时,需要的参数是目标超像素个数S.GKM生成超像素过程如下: (1) 首先,如果原始图像为RGB空间,需要先将其转化为CIELab颜色空间.转换过程为先将RGB转换到CIEXYZ颜色空间,如式(1)所示,然后再转换到CIELab颜色空间,如式(2)~式(4)所示. (1) (2) (3) (4) (2) 均匀初始化聚类中心点并利用GKM算法对图像中的像素点进行聚类. 图1展示了GKM算法生成超像素的效果,图1a为S=1 000时的分割结果;图1b为S=2 000时的分割结果;图1c为S=3 000时的分割结果. 图1 利用GKM算法生成超像素Fig.1 Superpixel generation based on GKM algorithm(a)—S=1 000; (b)—S=2 000; (c)—S=3 000. 参数S过大会产生分割现象,过小有可能分割比较粗糙,所以适中的参数S对于分割效果非常重要. 本文实验的硬件环境:CPU为Intel Core I7 4770kB,内存8 GB.程序的运行环境是Windows 7操作系统下的MATLAB R2013a.对于实验的数据集,本文实验使用国际公认的数据集VOC 2007.该数据集包括9 963张图片,共分成20个目标类. 实验部分首先将本文算法与Wang算法和ISLIC算法比较.图2分别展示了这3种算法的分割结果,各个算法选取的都是最优阈值,本文算法的S=2 000,而Wang算法和ISLIC算法的S=3 000.分割过程中最重要的是保证感兴趣区域(ROI)与实际分割区域之间的一致性.如图2所示,Wang算法由于更加关注算法效率,分割效果略有下降.ISLIC算法是对SLIC算法的改进,超像素的贴合度更高,分割效果比较好. 表1所示为三种算法的分割结果数据对比.利用PRI(probabilistic rand index)、VOI(variation of information)以及CR(covering rate)三个指标对分割结果进行评价.PRI值和CR值在区间[0,1]内,值越大说明分割结果越好;VOI值在区间[0,+∞)内,值越小说明分割结果越好.表中的1st代表图2中的第一列图片,2nd代表第二列图片,3rd代表第三列图片. 表1 分割结果对比Table 1 Comparison of segmentation results 表2展示了算法的执行效率对比.通过表2可以看出,Wang算法运行时间略低于本文算法,但是与平均值的对比可以体现出算法在运行速度上具有一定优势.所以总体而言,本文的算法在各项性能上都有一定提高. 表2 运行时间对比Table 2 Comparison of running time 本文分析了传统K-means算法的局限性,并针对这些不足引入全局K-means算法提出了改进的超像素分割算法.为了验证基于全局K-means算法的超像素分割方法的有效性,本文选取了Wang算法和ISLIC算法等相关算法作为实验参照.通过仿真实验验证,本文提出的改进算法获得了良好的分割效果. [ 1 ] 田丹,吴静飞,范立南. 水平集理论在磁共振脑图像分割中的模型研究[J]. 沈阳大学学报(自然科学版), 2013,25(4):298-302. (TIAN D,WU J F,FAN L N. Survey on model of level set in MR brain image segmentation[J]. Journal of Shenyang University(Natural Science), 2013,25(4):298-302.) [ 2 ] WANG S,LU H,YANG F,et al. Superpixel tracking[C]∥International Conference on Computer Vision. IEEE Computer Society, 2011:1323-1330. [ 3 ] CHANG J,WEI D,FISHER J W. A video representation using temporal superpixels[C]∥IEEE Conference on Computer Vision & Pattern Recognition. IEEE, 2013:2051-2058. [ 4 ] LIU M Y,TUZEL O,RAMALINGAM S,et al. Entropy rate superpixel segmentation[C]∥Proceedings of IEEE Conference on Computer Vision and Pattern recognition. Washington DC,USA: IEEE, 2011:2097-2104. [ 5 ] ZHANG Y,HARTLEY R,MASHFORD J,et al. Superpixels via pseudo-Boolean optimization [C]∥Proceedings of IEEE International Conference on Computer Vision. Washington DC, USA: IEEE, 2011:1387-1394. [ 6 ] BERGH M V D,BOIX X,ROIG G,et al. SEEDS: Superpixels extracted via energy-driven sampling[M]∥Computer Vision-ECCV 2012. Berlin Heidelberg: Springer, 2012:13-26. [ 7 ] WANG P,ZENG G,GAN R,et al. Structure-sensitive superpixels via geodesic distance[J]. International Journal of Computer Vision, 2013,103(1):1-21. [ 8 ] 惠转妮. 基于GlobalK-means的多维数据聚类算法研究及其GPU加速[D]. 西安:西安电子科技大学, 2012. (HUI Z N. Research on multidimensional data clustering algorithm based on globalK-means and its GPU acceleration[D]. Xi’an: Xidian University, 2012.) [ 9 ] 岳温川,王卫卫,李小平. 基于加权稀疏子空间聚类多特征融合图像分割[J]. 系统工程与电子技术, 2016,38(9):2184-2191. (YUE W C,WANG W W,LI X P. Multi-feature fusion image segmentation based on weighted-sparse subspace clustering[J]. Systems Engineering and Electronics, 2016,38(9):2184-2191.) [10] 陈恺,陈芳,戴敏,等. 基于萤火虫算法的二维熵多阈值快速图像分割[J]. 光学精密工程, 2014,22(2):517-523. (CHEN K,CHEN F,DAI M,et al.Fast image segmentation with multilevel threshold of two-dimensional entropy based on firefly algorithm[J]. Optics and Precision Engineering, 2014,22(2):517-523.) [11] 周晨航,田力威,赵宏伟. 基于改进萤火虫算法的二维Otsu图像分割法[J]. 沈阳大学学报(自然科学版), 2016,28(1):45-50. (ZHOU C H,TIAN L W,ZHAO H W. Image thresholding segmentation with 2-D otsu based on improved firefly algorithm[J]. Journal of Shenyang University(Natural Science), 2016,28(1):45-50.) [12] 许志远,王庸凯,孙康,等. 基于CLAHE的DSP实时去雾系统[J]. 沈阳大学学报(自然科学版), 2014,26(4):296-300. (XU Z Y,WANG Y K,SUN K,et al.DSP real-time fog removal system based on CLAHE[J]. Journal of Shenyang University(Natural Science), 2014,26(4):296-300.) 【责任编辑: 李 艳】 Superpixel Segmentation Method Based on GlobalK-means JiChangdong1,LiXiangze2,AoGuozheng3 (1. School of Geomatics, Liaoning Technical University, Fuxin 125105, China; 2. School of Computer Science and Engineering, Northeastern University, Shenyang 110819, China; 3. School of Electronics & Information Engineering, Liaoning University of Technology, Jinzhou 121001, China) In order to improve the performance of the superpixel segmentation, a superpixel segmentation method based on globalK-means algorithm is proposed. The algorithm uses the globalK-means algorithm to compute the superpixel clustering, optimizes the segmentation quality of the superpixel, and divides the target from the image according to the superpixel result after clustering. The experimental data came from the international recognized PASCAL VOC 2007 data sets. The experimental results show that compared with the Wang algorithm and ISLIC algorithm, the proposed segmentation algorithm has an average increase of 9.38%, 17.13%, 21.67% and 10.50% respectively in PRI, CR, VOI and run time, and has better performance. image segmentation; superpixel; globalK-means; cluster 2016-01-30 国家科技重大专项资助项目(2013ZX04007031); 国家科技重大专项资助项目(2012ZX01029001-002). 吉长东(1970-),男,辽宁锦州人,辽宁工程技术大学教授. 2095-5456(2017)03-0212-05 TP 391.4 A2 基于全局K-means的超像素分割
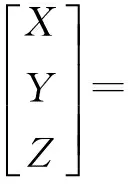

3 仿真结果及分析
4 结 语
