基于改进的灰色模型和支持向量机的风电功率预测

邵一川, 张 吉, 贾海波, 李 鑫, 马连博(沈阳大学 信息工程学院, 辽宁 沈阳 110044)



基于改进的灰色模型和支持向量机的风电功率预测

邵一川, 张 吉, 贾海波, 李 鑫, 马连博
(沈阳大学 信息工程学院, 辽宁 沈阳 110044)

使用组合模型进行了风速预测,然后在此基础上进行了风电功率的预测.利用灰色模型进行风速中确定性趋势预测,针对灰色GM(1,1)模型的建模机理和风速预测特点对其进行了改进,建立了改进的灰色GM(1,1)风速预测模型;同时使用支持向量机进行风速的随机性预测;用建立的组合预测模型输出的风速作为风电功率预测的一个输入,利用支持向量机模型进行了提前一小时的风电功率预测.算例表明,该方法可有效提高风速预测精度,进而提高风电功率的预测精度.

风电预测; 灰色理论; 支持向量机; 组合预测模型

作为一种洁净可再生能源,风能的开发得到了各国的高度重视.但是,风电的接入给电网带来了冲击,增大了电力调度的难度.为了减轻风电场对电网的冲击,增加系统容量,降低不利影响、提高电力市场环境下的风电系统上网能力[1],对风电功率进行准确预测势在必行.

风电功率预测方法,根据预测的物理量不同可分为两类:第一类是直接预测机组或风电场的输出功率;第二类为对风速进行预测,然后根据风电机组或风电场的功率曲线得到相应的功率输出[2-3].两类方法各有优缺点,方法一虽然考虑到功率的各种影响因素,但需要充分估计风速对风电机组输出功率的决定性影响,才能有较好的精度;第二类方法则需要对风速的影响考虑充分,但无法顾及影响功率输出的其他因素,而且实际的风速-功率特性是分散的一个带状区间,没有唯一的对应关系.

本文将上述两种方法结合,首先进行了风速预测,在此基础上又考虑其他各种影响因素进行了功率预测.由于风速预测中既有确定性趋势又有随机性趋势,因而使用组合模型能更好地表达其变化规律.本文利用灰色模型进行确定性趋势预测,使用支持向量机(Support Vector Machines,SVM)进行随机性预测,对两个模型的输出结果进行了等权叠加,最后又采用支持向量机建立了风电功率预测模型,实验结果验证了该方法的有效性.

1 灰色GM(1,1)建模原理

灰色系统理论是一种适用于研究贫信息、小样本、不确定性问题的方法[4].

灰色建模的过程是利用小样本、贫信息数据建立起来微分方程,而建模的过程是动态的信息提取、开发和加工的过程.

GM(1,1)是最常见的灰色模型,是对一个变量建立的一阶微分方程.GM(1,1)建模的原理是通过正数数据累加形成指数函数规律的序列,再用该序列去求生成函数,最后逼近生成序列是通过微分方程的解来实现的.

GM(1,1)模型建立的方法是[5-6]:

(1) 累加生成:设样本数据为拥有n个样本值的时间序列X(0),X(0)={X(0)(1),X(0)(2),…,X(0)(n)}通过累加生成新序列X(1)={X(1)(1),X(1)(2),…,X(1)(n)},累加的方法是

(2) 建立模型:GM(1,1)模型的微分方程为

式中,b为内生控制灰数(或灰色作用量);a为发展灰数(或待辨识参数).

对式(2)进行微分方程便转化为差分方程:

式中,

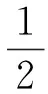
称为背景值.

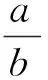
式中:

(3) 得到预测公式:求出参数a、b后,可通过求解微分方程得到预测模型:

对序列x(1)(k)做一次累减得到序列的还原值:

x(0)(k)=x(1)(k)-x(1)(k-1).

即

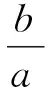
2 改进的GM(1,1)风速预测模型

针对GM(1,1)模型的建模机理和风速预测的特点,本文对GM(1,1)进行了一些改进,具体改进措施如下.

(1) 原始数据的平滑处理:对原始数据的累加处理减少了单个数据的激跳变,这样的处理对于平滑数据效果较好,但对于变化剧烈的数据,则没有好的效果.由于风速数据时间序列的随机性,非线性,激变性较强,因此通过累加方式还不能降低跳变数据对序列的影响.那么在累加处理前应当对原始数据序列展开预处理(平滑处理),这样可以进一步增强原始数据的发展趋势.预处理方法如下.

对数据序列的两个端点,分别采用下面的平滑处理公式:

始点:

终点:

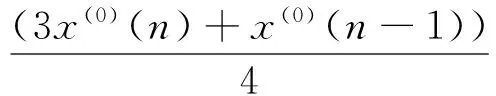
对数据序列中间的点采用下面的平滑公式:

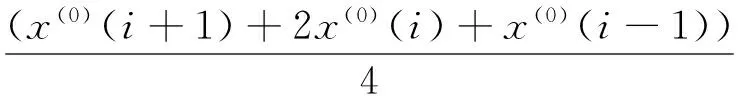
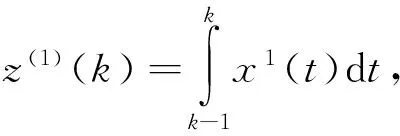
综合以上改进方法,本文建立了改进的GM(1,1)风速预测模型,并采用滚动更新的方法,每进行一次预测就对模型更新一次,即每次输入一个风速序列,预测完以后去掉序列的第一个值,并在序列的末尾加上最新的一个值,然后重新建模进行下一次预测.经过实验确定输入序列的元素个数为5时预测效果最好,由于所用数据为间隔20 min采样,故进行提前一小时预测时每次建模预测3个预测值,第一个值为提前20 min预测值,第二个为提前40 min,第三个为提前一小时,故取其第3个值;每次预测结束之后删除序列的第1个值,在序列末端加入1个采样值作为序列的第五个值,下次预测用更新以后的序列建模.预测模型建模流程图如图1所示.

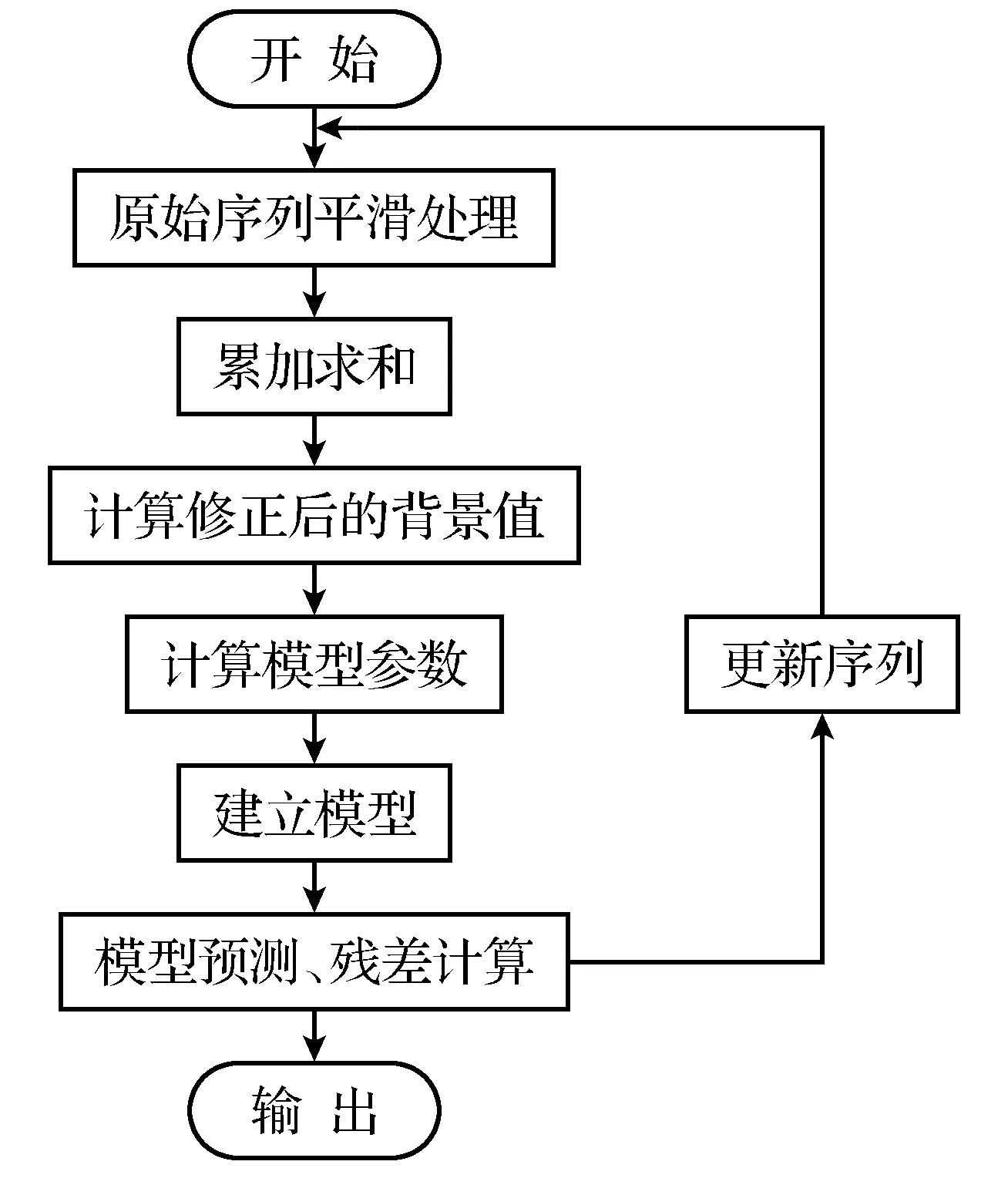
图1 改进的GM(1,1)模型预测流程图Fig.1 The flow chart of improved GM(1,1) model

3 支持向量机风速预测模型

支持向量机(Support Vector Machine,SVM)是Corinna Cortes和Vapnik等于1995年首先提出的,它在解决小样本、非线性及高维模式识别中表现出许多特有的优势,并能够推广应用到函数拟合等其他机器学习问题中.

在机器学习中,支持向量机(SVM,还支持矢量网络)是与相关的学习算法有关的监督学习模型,可以分析数据,识别模式,用于分类和回归分析.

支持向量机用于预测的原理是:假设样本集合为{(x1,y1)…(xi,yi),…,(xl,yl)},其中,xi∈Rn,yi∈R,i=1,2,3,…,l.则对该样本的回归表达式为

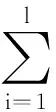
其中,

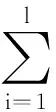
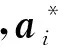
本文的支持向量机风速预测模型是单输入单输出模型,其输入为风速历史值,核函数选择径向基函数,采用交叉验证法和网格搜索法进行训练.预测时首先要选用一定量的样本对模型进行训练以确定模型参数,本文选择测试数据前一周的样本归一化数据作为训练数据,然后将前一小时历史风速归一化后的值输入训练好的模型进行预测.

4 复合功率预测模型的建模

基于支持向量机和灰色理论的复合功率预测模型如图 2所示.

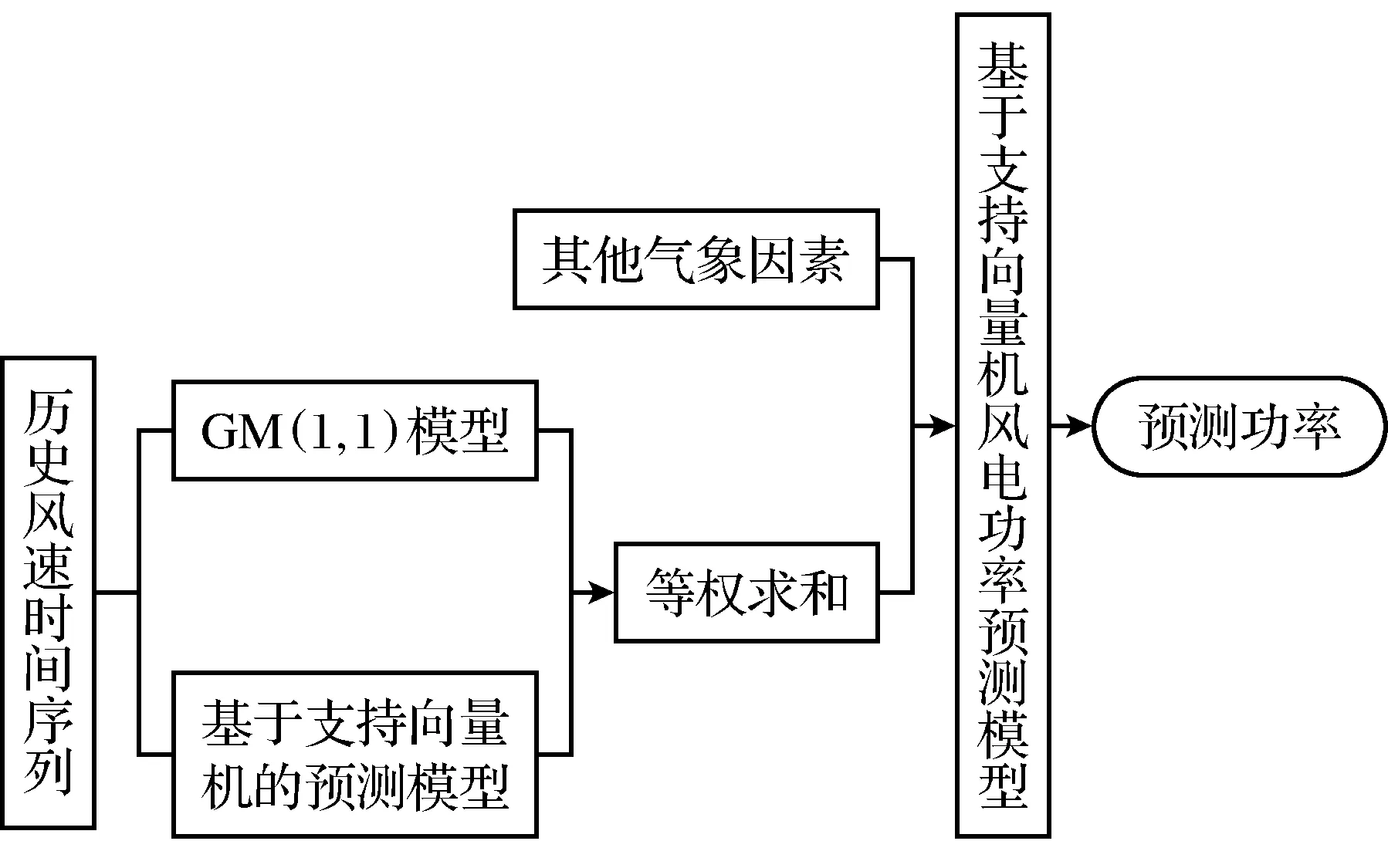
图2 灰色理论和支持向量机的复合功率预测模型

支持向量机的输入采用复合功率预测模型.利用预测风速、历史风速(上一时刻风速)、风向、温度的正弦和余弦、露点温度、风机震动等级、历史功率值作为支持向量机的输入.将风速立方以后再输入来增大风速的影响因子.同时考虑到风电功率与风速的非线性关系,将输入数据按照预测风速大小平均分成高、中、低三组,分别建立功率预测模型对输出功率进行预测.功率预测模型还选用常用的径向基函数作为核函数,同样采用交叉验证法和网格搜索法确定参数.

5 评价标准

对于风速预测一般选用绝对百分比误差(APE)、平均绝对百分比误差(MAPE)、均方根误差(MSE)[7]来对模型进行评价,其中:

式中:vP为预测风速;vR为实际风速;N为样本总数.

而对于风电功率预测,由于预测误差大小和风机容量有直接关系,为了更客观地评价预测效果,国际上普遍采用归一化绝对平均误差(eNMAE)和归一化均方根误差(eNRMSE)[8-9]作为预测误差指标,其定义为

国家能源局印发的《风电场功率预测预报暂行办法》[10]也给出了考核指标作为参考.根据《办法》主要考核指标包括准确率r1、合格率r2两项,其定义如下:

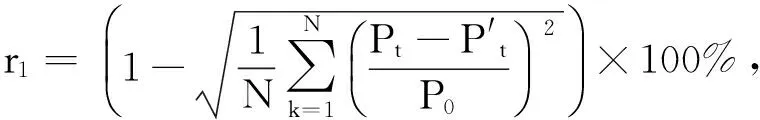
(20)

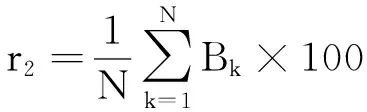
(21)

其中,

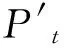
6 算例分析

本文采用美国HARLAN站点提供的天气情况数据及当地的风电场某机组的输出功率数据,数据采样时间间隔为20 min.采用Matlab的libsvm工具箱编写GM(1,1)和SVM的风速预测程序.

6.1 风速预测

在风速预测数据采用最近一周的数据作为训练数据来训练SVM模型,当最近一周的数据中风速小于2.0 m/s的采样点数m大于72点(一天的采样点数)时则把这些点从训练数据中删除,再从最近一段时间内选取m点加入训练数据.

选择11月19日0∶00到21日0∶00的数据进行测试.SVM模型采用交叉验证法确定的预测参数为C=0.1896,g=9.189 6组合模型和单一模型风速预测的结果如图 3所示,精度如表1所示从预测结果可以看出无论是平均绝对误差还是均方根误差组合模型都远小于两个模型单独预测.由此可见不同预测原理的模型组成的组合预测模型可以有效提高预测精度,减小预测误差.

表1 风速预测精度

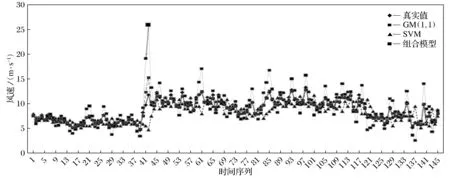
图3 预测风速与实际风速曲线Fig.3 The curve of predictive wind speed and real wind speed

6.2 风电功率预测

在进行功率预测时,本文建立了三个相互独立的SVM模型,对于这三个SVM模型,模型的输入数据包括历史风速等气象因素以及风速预测模型的输出数据,在训练模型时每个模型各选择400组最近的数据进行训练,采用实时风速代替预测风速.为了对不同的预测效果进行比较,在测试时分别将SVM模型预测的风速和组合模型预测的风速输入训练好的功率预测模型进行预测,对预测结果进行对比.

本文首先对11月19日0∶00到21日0∶00的数据进行测试.SVM模型采用交叉验证法确定的预测参数为C=16,g=0.020 617(低风速模型);C=27.857 6,g=1.741 1(中风速模型);C=1.741 1,g=0.329 88(高风速模型).第一天预测的结果如图 4所示.

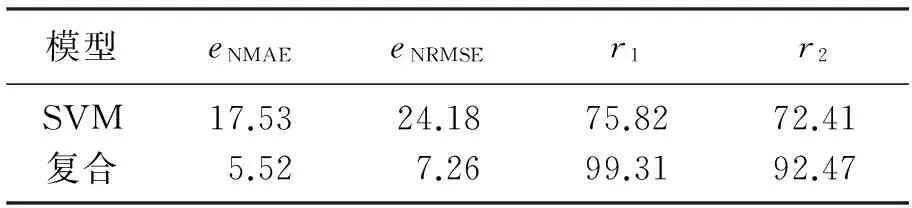
表2 功率预测的精度(1)

通过表2可以看出采用组合模型预测风速的各项预测指标均远好于采用SVM模型预测的结果,有效改进了预测效果,提高了预测精度,无论国际标准还是国内标准均能满足.

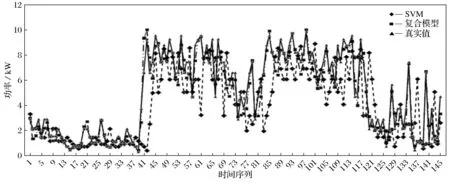
图4 预测功率与实际功率曲线(1)Fig.4 The curve of predictive power and actual power(1)

再对4月27日0∶00到29日0∶00的数据进行测试.SVM模型采用交叉验证法确定的预测参数为C=48.502 9,g=0.006 8012(低风速模型);C=1.741 1,g=0.189 46(中风速模型);C=256,g=0.189 46(高风速模型),第一天预测的结果如图5和表3所示.

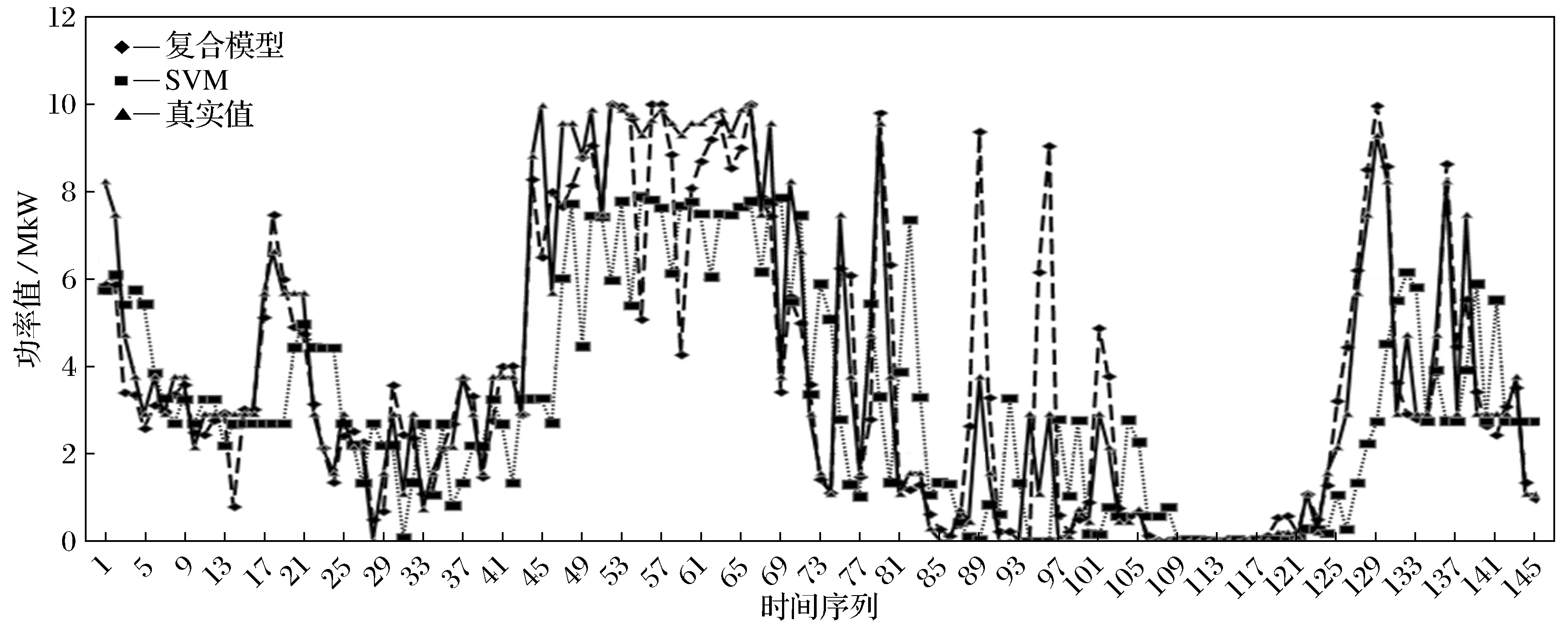
图5 预测功率与实际功率曲线(2)Fig.5 The curve of predictive power and actual power(2)

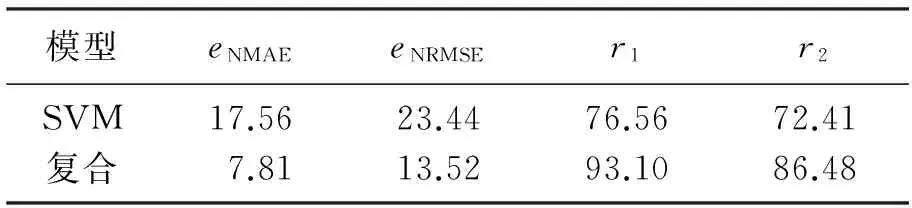
表3 功率预测的精度(2)

在这组数据中,虽然精度指标略逊于上组数据,但采用组合模型预测风速的结果同样远优于采用SVM模型预测的结果,同样能满足标准.

综合以上两组数据可知,虽然对于不同气象条件下的预测精度有一定的差异,但是无论在何种情况下复合预测模型都能有效地提高预测精度.

7 结 论

本文结合两种传统的风电功率预测思路,建立了一个风电功率复合预测模型,既避免对气象因素欠缺考虑的缺点,又避免了无法充分估计风速对风电机组输出功率的决定性影响的缺点.复合模型通过组合改进的GM(1,1)和支持向量机模型的预测结果进行了提前一小时的风速预测,达到了较高的精度.然后又在风速预测的基础上建立了基于支持向量机的风电功率预测模型,算例证明了模型的有效性.

[ 1 ] 范高峰,赵海翔,戴丽珠. 大规模风电对电力系统的影响和应对策略[J]. 电网与清洁能源, 2008,24(7):44-48. (FAN G F,ZHAO H X,DAI L Z. On the impact of wind power system and countermeasures[J]. Power Grid and Clean Energy, 2008,24(7):44-48.)

[ 2 ] HONG C,LIN W M,WEN B Y. Overview on prediction methods of wind speed and wind power[J]. Advances of Power System & Hydroelectric Engineering, 2011,27(1).

[ 3 ] LIU C,FAN G F,WANG W S. A combination forecasting model for wind farm output power[J]. Power System Technology, 2015,33(13):74-79.

[ 4 ] 邓聚龙. 走向世界的灰色系统理论[C]∥第十届全国灰色系统学术讨论会大会报告. 北京, 2002. (DENG J L. The theory of grey system in the world[C]∥The report of the Tenth National Conference on Grey System Academic Conference. Beijing, 2002.)

[ 5 ] DENG J L. Control problems of systems grey[J]. Systems & Control Letters, 1982,1(5):288-294.

[ 6 ] KUN L W,YI F H,MEI L Y. The Development of GM(1,1) error toolbox[C]∥IEEE International Conference on Intelligent and Advanced Systems. 2007:276-279.(in Chinese)

[ 7 ] 邵璠,孙育,梁岚珍. 基于时间序列法的风电场风速预测研究[J]. 华东电力, 2008,36(7):21-24. (SHAO F,SUN Y,LIANG L Z. Wind farms based on time series prediction of[J]. East China Electric Power,, 2008,36(7):21-24.)

[ 8 ] 王丽婕,冬雷,廖晓钟,等. 基于小波分析的风电场短期发电功率预测[J]. 中国电机工程学报, 2015,29(28):30-33. (WANG L J,Dong L,LIAO X Z,et al. Wind power generation based on wavelet analysis[J]. Proceedings of the Chinese Society of Electrical Engineering, 2015,29(28):30-33.)

[ 9 ] SIDERATOS G,HATZIARGYRIOU N D. Anadvanced statistical method for wind power forecasting[J]. IEEE Transactions on Power Systems, 2007,22(1):258-265.

[10] 国能新能[2011]177号. 风电场功率预测预报暂行办法的通知[S]. (Notice of the Interim Measures for the power prediction and forecast of national renewable energy[2011]177 wind farm[S].)

【责任编辑: 肖景魁】

Wind Power Prediction Based on Improved Grey Theory and SVM

ShaoYichuan,ZhangJi,JiaHaibo,LiXin,MaLianbo

(School of Information Engineering, Shenyang University, Shenyang 110044, China)

The wind speed prediction is carried out using the combined model, and then the wind power is predicted. The wind speed is predicted by using the gray model. Aiming at the modeling mechanism of gray GM(1,1) model and the characteristics of wind speed prediction, an improved gray GM(1,1) wind speed prediction model is established; at the same time, the support vector machine is used to predict the wind speed; the wind speed output from the established combined prediction model is used as an input for wind power prediction, and the support vector machine model is used to predict wind power one hour ahead of time. The numerical examples show that this method can effectively improve the prediction accuracy of wind speed and improve the prediction accuracy of wind power.

wind power prediction; grey theory; support vector machines(SVM); combination prediction model

2017-01-17

辽宁省博士启动基金资助项目(201601217); 中国博士后基金资助项目(2016172709).

邵一川(1978-),男,辽宁沈阳人,沈阳大学副教授。

2095-5456(2017)03-0217-06

TP 3-0

A