连续刚构桥跨中横隔板设计参数

邬晓光, 贺 攀, 李艺林, 冯 宇(长安大学 桥梁与隧道陕西省重点试验室, 陕西 西安 710064)



连续刚构桥跨中横隔板设计参数

邬晓光, 贺 攀, 李艺林, 冯 宇
(长安大学 桥梁与隧道陕西省重点试验室, 陕西 西安 710064)

从连续刚构桥设计实际出发,利用Midas Fea建立局部空间实体模型,分析了16m宽的箱梁跨中设置横隔板后对跨中及附近区段顶、底板横向应力分布的影响.研究结果表明,横隔板的设置可以有效改善跨中部位顶板及底板的横向应力分布,并且能削弱应力峰值,有效控制跨中底板裂缝的开展.通过改变横隔板的厚度、挖空率和数量得出横隔板的最佳设计参数.可为连续刚构桥梁的设计提供一定的参考.

连续刚构桥; 宽箱梁; 有限元法; 跨中; 横隔板; 设计参数

由于连续刚构桥跨中预应力孔道较多,截面面积削弱明显,加上张拉的底板纵向预应力对混凝土产生作用向下的径向力[1],使得跨中部位底板常常产生纵向裂缝,在恶劣环境(如海洋环境)裂缝的产生会加速钢筋的锈蚀[2],加之考虑温度对箱梁整体的作用[3],使得纵向裂缝的产生对桥梁的耐久性产生很大的影响.文献[4-7]研究了墩顶横隔板受力,论述了横隔板对于横向刚度的贡献,在跨中位置加设一道横隔板可以显著改善跨中位置底板和腹板的应力状态[8];文献[1]和文献[9-10]的研究表明,在跨中以及附近部位加设矮肋可以改善底板横向拉应力过大的问题.跨中加设一道横隔板虽然可以改善跨中底板应力状态,但跨中位置以外区域应力状态是否得到改善,以及底板横向拉应力过大的区域是否仍然存在等问题不得而知.加设矮肋并不能改善顶板的横向应力,并且矮肋的最佳厚度尺寸无法确定,现行规范也未对连续刚构桥跨中横隔板相关尺寸做出明确的规定[11-12].

本文从连续刚构桥设计实际出发,分析16 m宽箱梁跨中顶、底板横向应力分布及大小,以连续刚构桥A为依托,通过对跨中设置横隔板,采用有限元软件研究其对跨中顶、底板横向应力的影响,进而对横隔板设计参数进行优化研究,提出横隔板设置的最佳厚度、最佳数量以及最佳挖空率.

1 工程概况

某桥A为四跨(65+2×120+65)m预应力混凝土连续刚构桥.采用悬臂浇筑施工,三向预应力体系,单箱单室截面,箱梁横断面如图1所示.

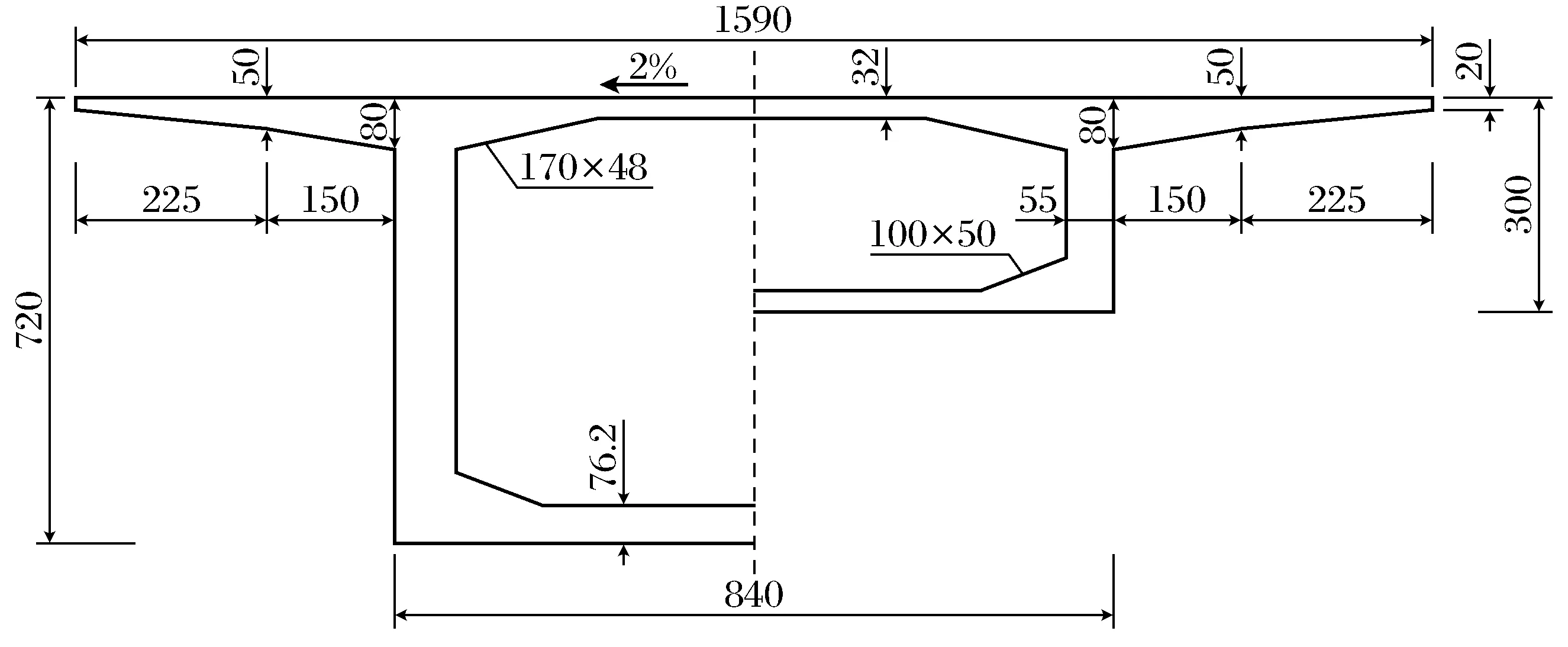
图1 桥A箱梁横断面图(单位:cm)Fig.1 Box girder cross section of bridge A

连续刚构桥A箱梁根部高度7.2 m,跨中梁高3.0 m,其间梁高按1.8次抛物线变化.箱梁顶板宽15.9 m,底板宽8.4 m,顶板厚0.32 m,底板厚由跨中0.32 m按1.8次抛物线变化至根部0.80 m,腹板厚跨中段为0.55 m、根部变为0.7 m,渐变段长4.0 m.

主桥中跨底板纵向预应力采用17ΦS15.20钢绞线,锚下张拉控制应力为1 395 MPa.主桥竖向预应力采用JL32高强度精轧螺纹钢筋,设计张拉力560 kN,腹板内采用双肢布置.

2 计算模型

2.1 平面杆系及空间实体模型

使用Midas Civil有限元软件建立平面杆系模型,如图2所示(顺桥向为x轴,横桥向为y轴).

图2 全桥有限元平面杆系模型
Fig.2 Finite element plane model of full-bridge

使用Midas Fea 有限元软件建立空间模型,模拟底板纵向预应力张拉对底板受力的影响,研究横隔板布置数量,建立图3所示的局部模型.

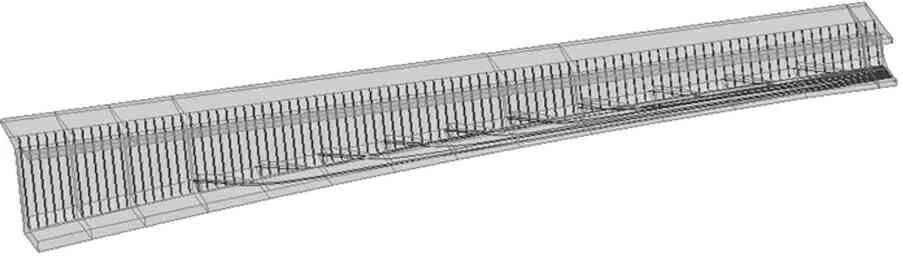
图3 桥A跨中1/2局部模型及钢束布置图

Fig.3 1/2 local model and layout of steel bundles of bridge A

模型的尺寸均采用设计图尺寸,边界条件由全桥平面杆系模型计算得到.其中截取的最左端轴力为-161 191.46 kN,剪力为16 255.51 kN,弯矩为462 341.79 kN·m.截取的最右端轴力为-157 644.8 kN,剪力为19 078.57 kN,弯矩为395 979.19 kN·m.在两端析取网格面,将整体模型中得到的内力施加在两端网格面重心处.

在取出的局部模型中增设横隔板,其布置如图4所示,横隔板具体的尺寸将在下文中阐述.

图4 桥A横隔板布置示意图
Fig.4 Layout diagram of diaphragms of bridge A

2.2 计算工况及结果分析

(1) 确定横隔板最佳厚度.分6种工况分析比较,工况1为考虑箱梁自重、二期恒载和纵向、竖向预应力作用;工况2、3、4、5、6分别为载荷不变,跨中最大悬臂处增设一道(1#)厚度为40、45、50、55和60 cm的横隔板,分析增设不同厚度横隔板时对跨中底板应力的改善情况,以确定横隔板的最佳厚度.结果如表1所示.

表1表明未设置横隔板时横向位置上跨中底板出现拉应力,最大拉应力出现在腹板与底板交接处附近,其值为2.56 MPa;中间位置拉应力为1.60 MPa,横向上应力分布不均匀,呈现出明显的剪力滞效应.由分析可知,设置横隔板会使底板应力得到明显改善,横隔板厚度为55 cm时应力改善最为明显,腹板处拉应力降低至1.29 MPa,中间位置拉应力降低至1.18 MPa;横隔板厚度为60 cm时,底板应力改善较横隔板厚为55 cm时不明显.从经济角度及最大程度减少自重的原则考虑,确定横隔板的合理厚度为55 cm.

表1 跨中底板横向应力分布情况Table 1 Transverse stress distribution at bottom plate of cross section

(2) 确定横隔板最佳挖空率.横向加劲肋高度在40～50 cm时,对横向应力影响显著.随着加劲肋高度的增加,横向拉应力和压应力均减小,但变化幅度不是很大.各截面处横隔板的挖空方式见图5,为简化建模,保持H1为40 cm固定不变,其中L为箱梁中心线至最内侧预应力孔道中心线的距离,本文中L=130 cm,通过调整H2的大小实现挖空率的改变.

分6种工况研究横隔板不同挖空率对箱梁空间应力的影响.工况1为考虑箱梁自重、二期恒载和纵向、竖向预应力作用;工况2、3、4、5、6分别为载荷不变,考虑横隔板最佳厚度和最佳数量,跨中最大悬臂位置处增设挖空率为25%、30%、35%、40%、45%的厚度为55 cm的横隔板.合龙段顶板、底板横向应力对比分析如下.

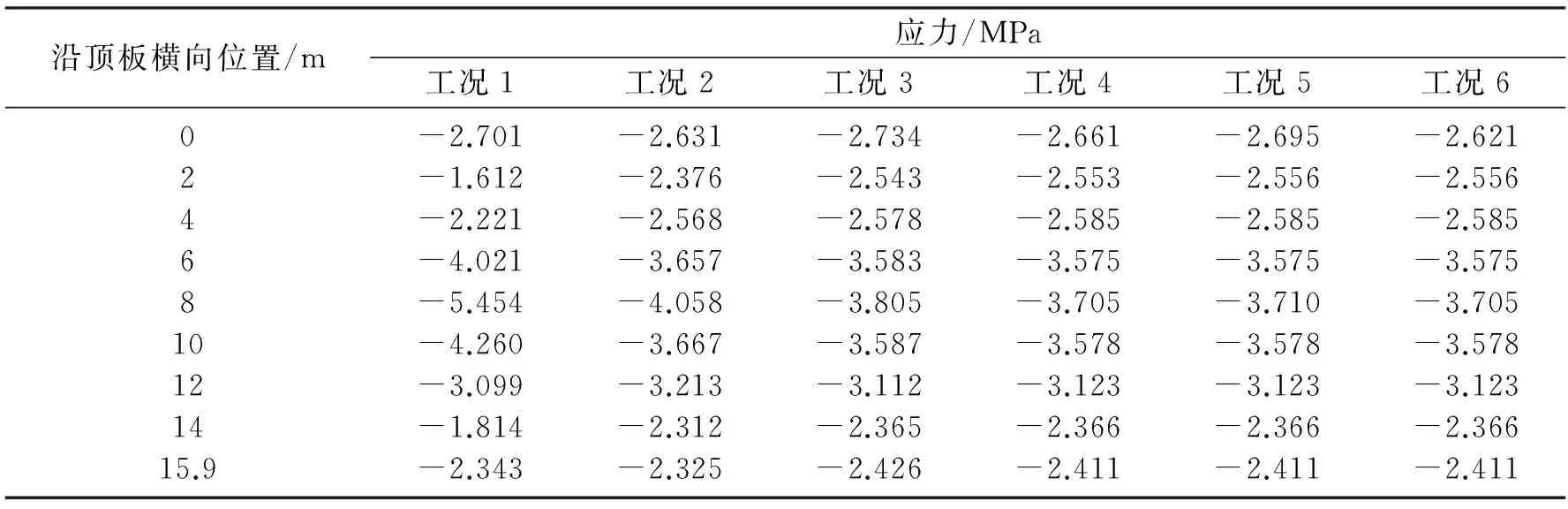
表2 合龙段顶板横向应力分布情况Table 2 Transverse stress distribution at roof plate of closure section

由表2可知,顶板横向应力主要为压应力,与前文叙述相同,与腹板交界处附近压应力最小,为1.61 MPa.顶板中间压应力最大,峰值为5.45 MPa;增设横隔板可以使得顶板横向应力分布更加均匀,但不同挖空率对顶板横向应力分布以及应力大小改变不大.当挖空率为45%时,由于顶板处横隔板高度变小,对顶板横向应力改善效果逐渐减弱,因此确定横隔板最佳挖空率为35%.

(3) 确定横隔板最佳数量.基于以上确定出的横隔板合理厚度以及最佳挖空率,分6种工况研究横隔板设置的最佳数量.工况1为考虑箱梁自重、二期恒载和纵向、竖向预应力作用;工况2、3、4、5、6分别为载荷不变,横隔板厚度为55 cm,挖空率为35%,增设横隔板1#;增设横隔板1#、2#;增设横隔板1#～3#;增设横隔板1#～4#;增设横隔板1#～5#.跨中合龙段及合龙段左右一定范围内每个块段的中点处顶、底板的横向应力比较分析结果如下.

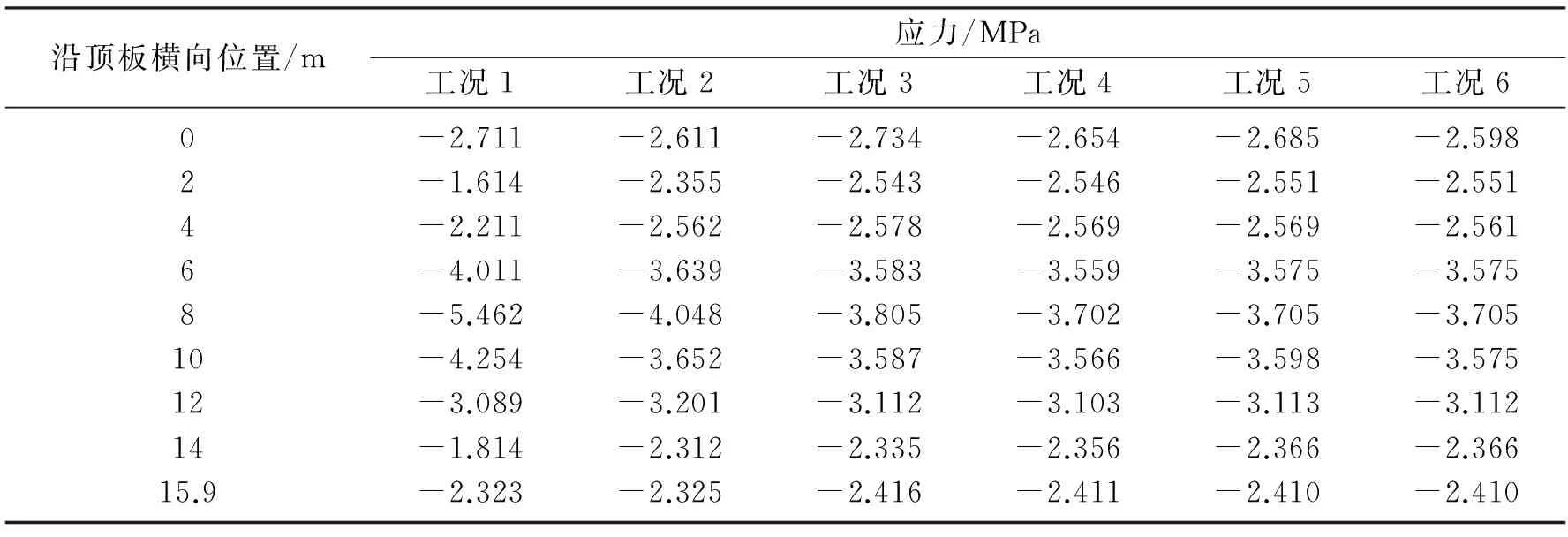
表3 合龙段顶板横向应力分布情况Table 3 Transverse stress distribution at roof plate of closure section

由表3、表4可知,对于合龙段位置,最大悬臂处增设一道横隔板能够有效改善顶板和底板横向应力的分布,削弱应力峰值.横隔板数量继续增加,应力值虽减小,但减小幅度有限.当继续增加横隔板数量时,由于新增加的横隔板距离跨中位置较远,对此位置的影响微乎其微.

表4 合龙段底板横向应力分布情况Table 2 Transverse stress distribution at bottom plate of closure section

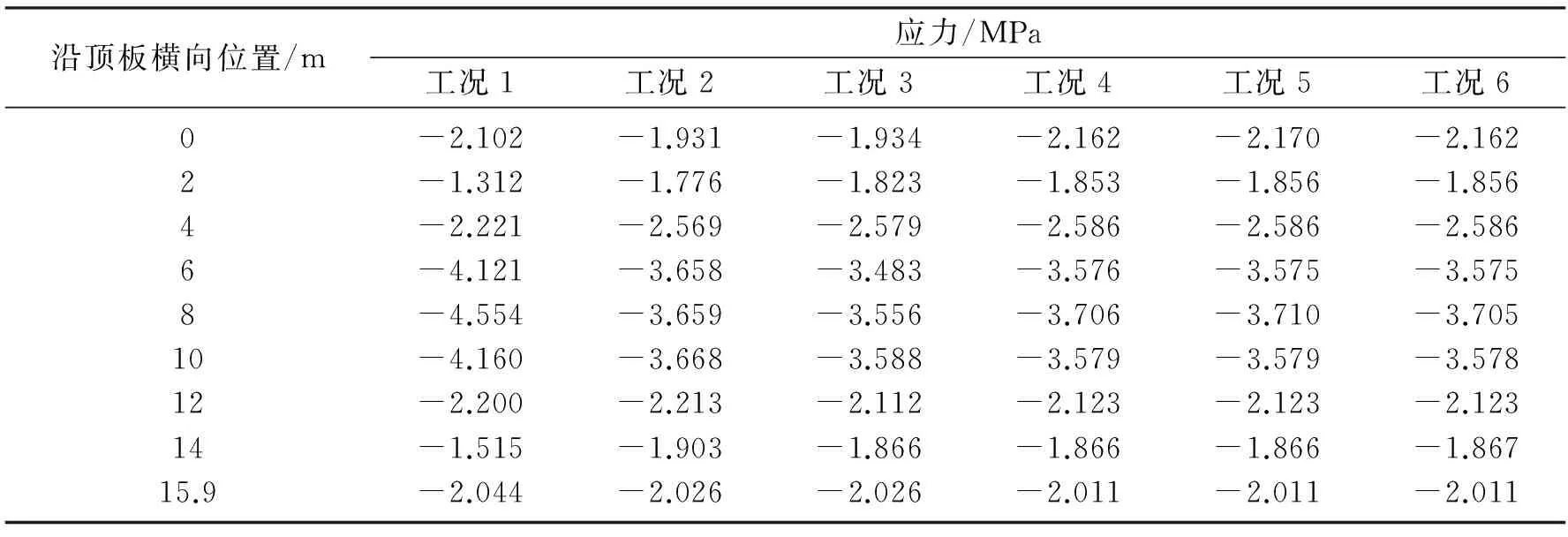
表5 15号块段中间位置顶板横向应力分布情况Table 5 Transverse stress distribution at roof plate of 15# block

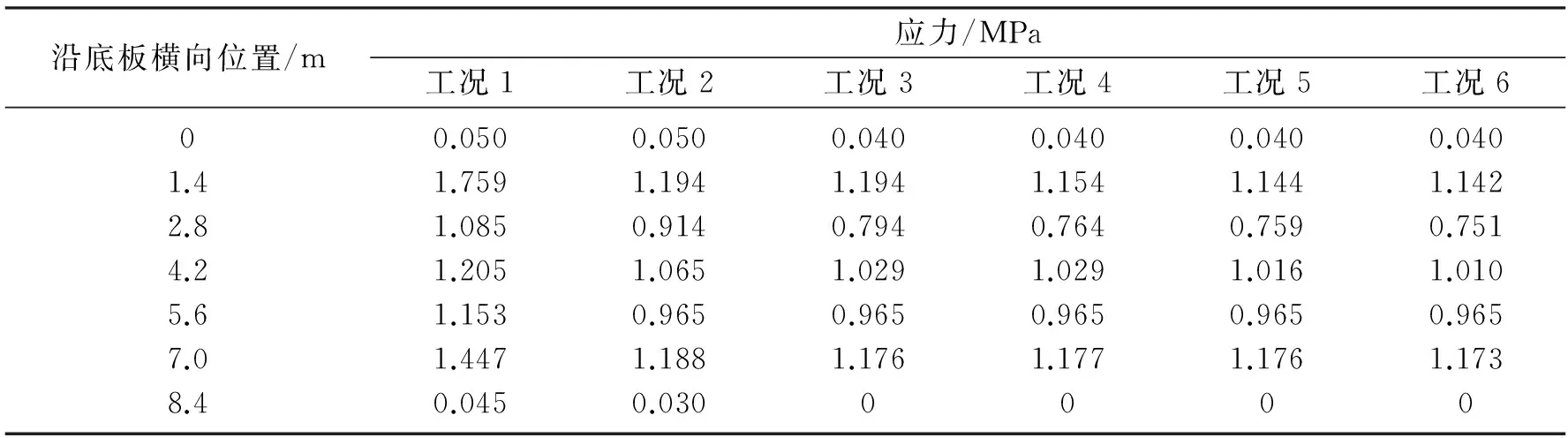
表6 15号块段中间位置底板横向应力分布情况Table 6 Transverse stress distribution at bottom plate of 15# block

由表5、表6可知, 15号块段顶板和底板应力分布不均,顶板上最大压应力为4.55 MPa,底板上最大拉应力为1.76 MPa.在工况2和工况3下增设横隔板1#和2#对其顶、底板横向应力影响较大,继续增加横隔板数量影响较小.

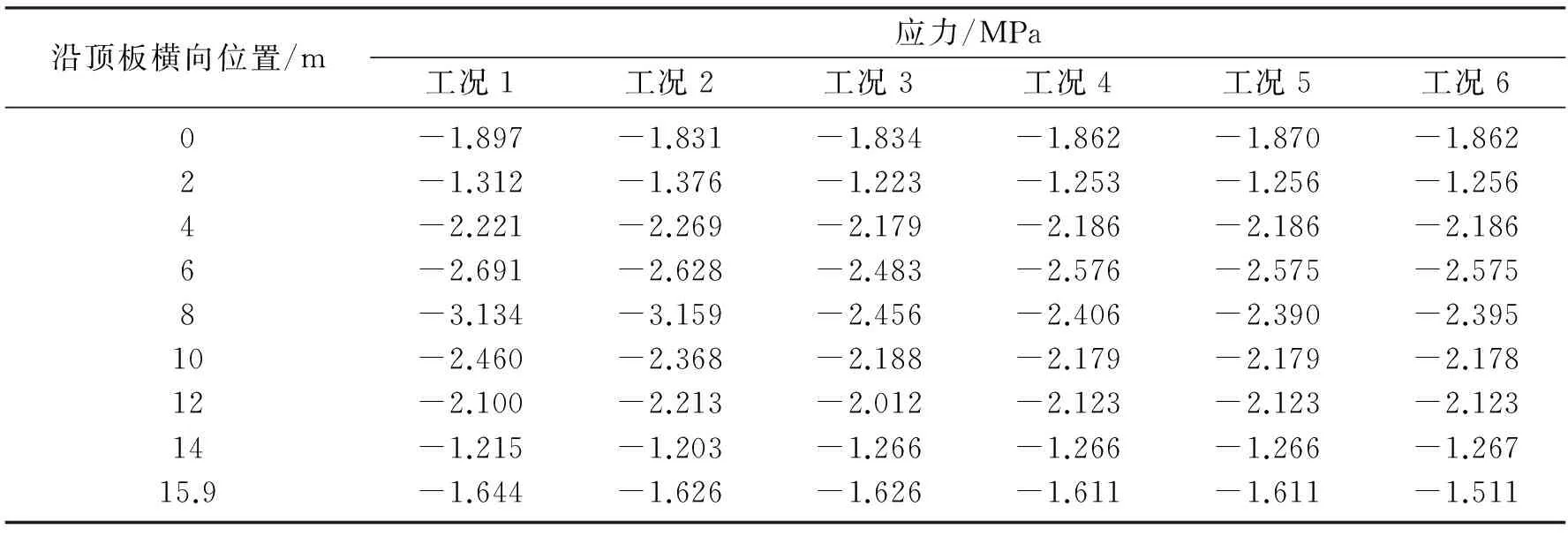
表7 14号块段中间位置顶板横向应力分布情况Table 7 Transverse stress distribution at roof plate of 14# block

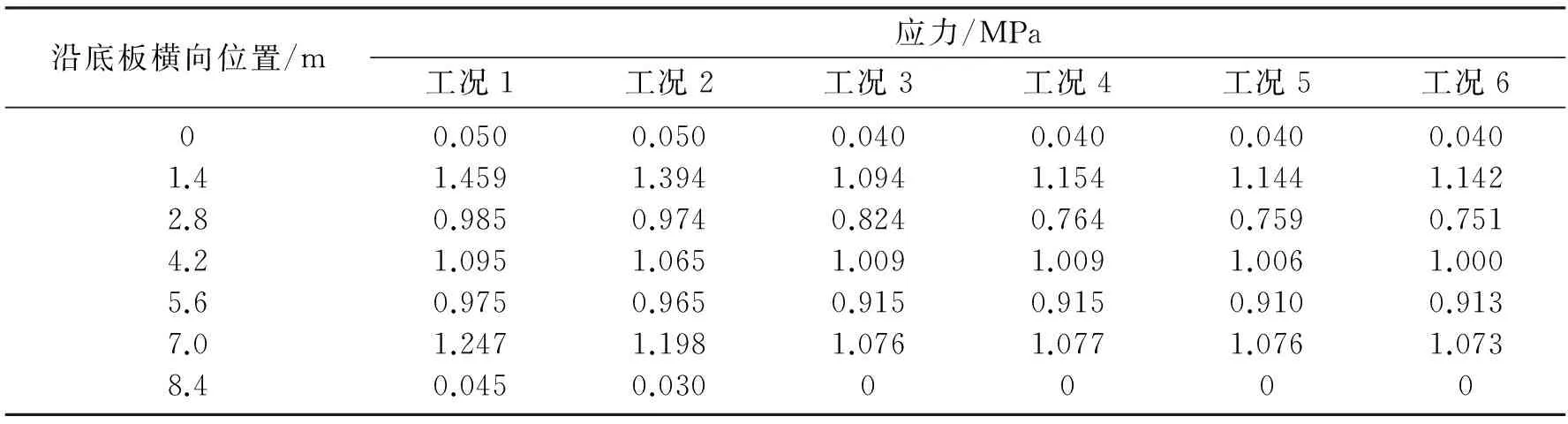
表8 14号块段中间位置底板横向应力分布情况Table 8 Transverse stress distribution at bottom plate of 14# block

由表7、表8可知,14号块段顶板最大压应力与底板最大拉应力数值明显减小;增设横隔板1#对14号块段横向应力的影响较小;当增设横隔板2#和3#时,能够有效改善该区域应力分布,继续增设横隔板对该区域应力的改善作用不明显.

表9 13号块段中间位置顶板横向应力分布情况Table 9 Transverse stress distribution at roof plate of 13# block

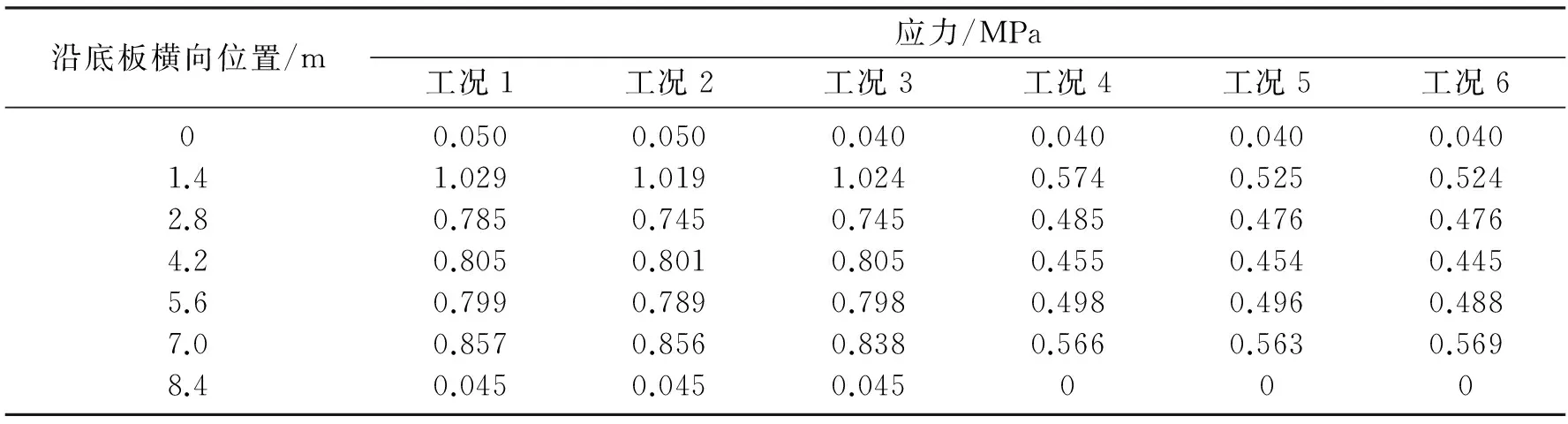
表10 13号块段中间位置底板横向应力分布情况Table 10 Transverse stress distribution at bottom plate of 13# block

由表9、表10可知,13#块段顶板最大压应力出现在中间位置,其值为2.13 MPa,底板最大拉应力为1.03 MPa.增设横隔板1#和2#对13#块段横向应力的影响较小,当增设横隔板3#和4#时,横向应力数值明显减小,继续增加横隔板数量影响较小.

对合龙段及15#～13#块段的分析中可以发现,沿跨中位置向墩顶两侧的顶、底板横向应力均呈减小趋势.通过设置横隔板,以上区域的横向应力分布均得到较大改善.在跨中设置2～3道横隔板时可以有效改善顶、底板横向应力,继续增加横隔板的数量时作用不大.因此,横隔板的最佳数量为2～3道.

3 结论与建议

(1) 连续刚构桥梁跨中设置横隔板不但能增加箱梁横向刚度,而且可以有效减小顶、底板横向应力,改善横向应力分布.跨中横隔板最佳厚度为55 cm,继续增加横隔板的厚度,对底板应力分布无明显影响.建议在进行16 m宽箱梁桥设计时跨中横隔板厚度取为50～60 cm,宽度大于16 m时横隔板厚度可适当加大.

(2) 横隔板的最佳挖空率为35%.设计时参照图5,L与H1不变,L可以取箱梁底板与腹板交接处倒角的长度,H1取值为40～50 cm.通过改变H2达到最佳挖空率,

(3) 通过改变横隔板的数量,得出最佳设置数量为2～3道.建议在设计时第一道横隔板设置在最大悬臂位置,然后再向两侧增设其他横隔板,跨径较大时可以适当增加其数量,但数量增加时需考虑自重对结构的影响.

[ 1 ] 胡云耀,常柱刚,胡汉渝. 关于增设矮肋法防治大跨径连续刚构桥箱梁底板纵向裂缝问题的探讨[J]. 中外公路, 2009,29(2):145-148. (HU Y Y,CHANG Z G,HU H Y. Discussion on the problem of preventing longitudinal cracks in the bottom slab of long-span continuous rigid frame bridge by adding low rib method[J]. Journal of China & Foreign Highway, 2009,29(2):145-148.)

[ 2 ] 林辉,张红显,邬晓光. 福建海域钢筋混凝土梁压弯刚度研究[J]. 沈阳大学学报(自然科学版), 2016,28(5):402-404. (LIN H,ZHANG H X,WU X G. Stiffness of reinforced concrete beam in Fujian sea area[J]. Journal of Shenyang University(Natural Science), 2016,28(5):402-404.)

[ 3 ] 钱若霖,冯宇. 陕西地区连续刚构桥温度梯度时变效应[J]. 沈阳大学学报(自然科学版), 2016,28(6):503-507. (QIAN R L,FENG Y. Temperature gradient effect of continuous rigid frame bridge in Shaanxi[J]. Journal of Shenyang University(Natural Science), 2016,28(6):503-507.)

[ 4 ] 何勇,卢小锋,王世发. 连续刚构0#块横隔板受力分析研究[J]. 公路交通科技(应用技术版), 2011(8):38-42. (HE Y,LU X F,WANG S F. Stress analysis of continuous rigid frame 0#block[J]. Journal of Highway and Transportation Research and Development(Application Technology), 2011(8):38-42.)

[ 5 ] 李胜华,周志祥,张鑫. 墩顶横隔板对连续刚构箱梁顶板力学性能的影响[J]. 重庆交通大学学报(自然科学版), 2007,26(4):3-5,28. (LI S H,ZHOU Z X,ZHANG X. Influences of diaphragn at the root of pier on the behaviors of roof board[J]. Journal of Chongqing Jiaotong University(Natural Science), 2007,26(4):3-5,28.)

[ 6 ] 于高志. 龙华松花江特大桥零号块横隔板应力分析[D]. 哈尔滨:东北林业大学, 2008. (YU G Z. The stress analysis of the cross diaphragm in segment No.0 for the Longhua super large bridge[D]. Harbin: Northeast Forestry University, 2008.)

[ 7 ] 王微嘉,罗鸣,罗实. 连续刚构桥0号块横隔板的构造与受力分析[J]. 路基工程, 2010,28(3):151-154. (WANG W J,LUO M,LUO S. Structure and stress analysis of cross diaphragm of segment No.0 in continuous rigid frame bridge[J]. Subgrade Engineering, 2010,28(3):151-154.)

[ 8 ] 孙学先,陈小勇,延力强. PC箱梁横隔板对其截面应力影响的空间分析[J]. 兰州交通大学学报, 2008,27(6):8-11. (SUN X X,CHEN X Y,YAN L Q. Spatial analysis of diaphragms of PC box girder effecting on the section stress[J]. Journal of Lanzhou Jiaotong University, 2008,27(6):8-11.)

[ 9 ] 葛万光,叶见曙,马莹. 横向加劲肋对箱梁底板受力的作用分析[J]. 交通标准化, 2011,36(23):133-136. (GE W G,YE J S,MA Y. Mechanical analysis of transverse stiffener effect on bottom slab of box girder[J]. Transportation Standardization, 2011,36(23):133-136.)

[10] 李旺丰. 跨中横向加劲肋对箱梁底板受力性能的影响[J]. 现代交通技术, 20085(1):66-70. (LI W F. Mechanical analysis of transverse stiffener effect on bottom slab of box girder[J]. Journal of Shandong Jiaotong University, 2008,5(1):66-70.)

[11] 公路桥涵设计通用规范: JTG D60—2015[S]. 北京:人民交通出版社, 2015. (General specifications for design of highway bridges and culverts: JTG D60-2015[S]. Beijing: China Communications Press, 2015.)

[12] 公路钢筋混凝土及预应力混凝土桥涵设计规范:JTG D62—2004[S]. 北京:人民交通出版社, 2004. (Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts: JTG D62-2004[S]. Beijing: China Communications Press, 2004.)

【责任编辑: 赵 炬】

Design Parameters of Diaphragmin Middle Span of Continuous Rigid-Frame Bridge

WuXiaoguang,HePan,LiYilin,FengYu

(Key Laboratory of Bridge and Tunnel of Shaanxi Province, Chang’an University, Xi’an 710064, China)

Based on the design of continuous rigid frame bridge, a local entity model space is established with software “Midas/Fea”. The propose is to study the influence for transverse stress distribution in top and bottom plates of middle span section and nearby after setting the diaphragms in 16m wide box beam. The results show that diaphragms can effectively improve the transverse stress across the top and bottom plates, as well as, weaken the peak of the stress, and it can control the emergence of cracks. The vintage design parameters of diaphragm are gotten by changing the thickness, hollowed out rate and quantity of the diaphragm. The conclusions and recommendations can provide a reference for the design of continuous rigid frame bridges.

continuous rigid frame bridge; wide box beam; finite element method; middle span; diaphragm; design parameters

2017-01-05

陕西省交通运输厅科技资助项目(13-25k).

邬晓光(1961-),男,湖北黄冈人,长安大学教授,博士生导师.

2095-5456(2017)03-0223-06

U 441

A