正交各向异性钢筋混凝土板的应力及应变分析

钟浩, 印长俊, 方宏华

(湘潭大学 土木工程与力学学院, 湖南 湘潭, 411105)

正交各向异性钢筋混凝土板的应力及应变分析

钟浩, 印长俊, 方宏华

(湘潭大学 土木工程与力学学院, 湖南 湘潭, 411105)

为了研究正交各向异性材料的应力、应变及弹性模量等力学参数, 本文从材料的物理力学特性出发, 推导了正交各向异性材料的弹性本构方程。用有限元分析软件模拟得到了正交各向异性钢筋混凝土板在自重与受荷作用下的应力、应变及板中挠度值。对比分析了视钢筋混凝土板为各向同性时的应力及应变情况。发现2种情况下的应力、应变及板中挠度值与实验数据均较接近, 因此, 本文的有限元分析方法是可行性的。由于2种情况下模拟结果相近, 因此可视正交各向异性材料为各向同性进行分析, 以简化分析过程。

正交各向异性; 钢筋混凝土板; 应力; 应变; 有限元分析

建筑材料中存在大量的正交各向异性材料[1], 钢筋混凝土板就是典型的正交各向异性材料。对于各向异性材料而言, 确定其物理特性需要21个独立的弹性常数, 而在正交各向异性材料中, 由于垂直于对称面上的方向为弹性主方向, 在此方向上, 材料具有相同的弹性特性。因此, 确定正交各向异性材料应力、应变等物理特性所需的独立常数为9个。在以往对钢筋混凝土板的有限元分析中, 将钢筋混凝土等水泥基材料视为钢筋和混凝土2种材料的组合, 提出了一系列的计算模型, 比如将钢筋与混凝土分别划分单元, 或根据2种材料的相对位置进行力学性能的均匀化处理[2], 建立能代表宏观力学性能的细观代表性单胞单元, 即在对水泥基材料进行应力及应变分析时, 各向采用同一弹性模量、泊松比等力学参数以简化计算。

本文通过对实际案例中的钢筋混凝土板中的钢筋与混凝土等材料物理参数的提取, 计算确定正交各向异性材料所需的9个独立常数, 经过有限元建模及分析计算, 得到在考虑水泥基材料正交各向异性情况下材料的应力及应变结果, 并将此结果与将钢筋混凝土板视为各向同性情况下的应力及应变结果进行比较分析。

1 弹性本构方程与力学参数的确定

1.1 弹性本构方程

正交各向异性材料中, 将平行弹性主方向的方向轴称为弹性主轴, 用X、Y和Z表示这3个主轴。根据广义虎克定律, 弹性应力、应变关系为:

式中, Ei为i方向弹性模量; Gij为i、j左边轴间的剪切模量; uij为i方向作用拉(压)应力引起j方向缩(伸)的泊松比。根据弹性矩阵的对称性有Exμyx= Eyμxy, Eyμzy= Ezμyz, Ezμxz= Exμzx, 因此, 式(2)中的12个常数中的9个是独立的。为求得式(1)中工程常数与弹性系数间的关系, 计算(2)式的逆矩阵可得: dxx=。该9个参数即为计算正交各向异性材料所需9个独立参数, 其中。

1.2 弹性力学参数确定

本文所采用的基本假设[3]有: 钢筋与混凝土之间没有相对滑移, 两者是相互粘结的; 钢筋混凝土板线弹性宏观均匀、宏观正交各向异性, 且没有初始应力。从假设条件下的钢筋混凝土板中取代表性结构微元如图1所示。

图1 钢筋混凝土板结构单元

由于本文所采用钢筋混凝板中的钢筋为双层双向设置, 对板下表面受拉以及上表面受压时的裂缝开展均可产生明显的控制和约束作用[4]。混凝土在受拉作用下极易产生裂缝, 裂缝将使混凝土产生应力重分布, 从而加速混凝土的破坏, 也使得对混凝土应力及应变分析变得复杂[5]。

本文所采用实验中的钢筋混凝土板在双层双向钢筋的约束下, 受自身荷载与均布荷载的作用, 在受力方向并未出现明显的裂缝, 裂缝开展均在受拉钢筋保护层范围内, 处在线弹性假设阶段[6]。因此, 本文假设在混凝土板受力方向上的刚度保持不变。

将钢筋看成纤维材料, 正交分布于混凝土中, 形成混凝土复合材料, 根据复合材料的性质来确定其各项弹性力学参数。沿钢筋分布方向设为坐标轴X、Y。设在X轴方向上有作用力Fx, 则

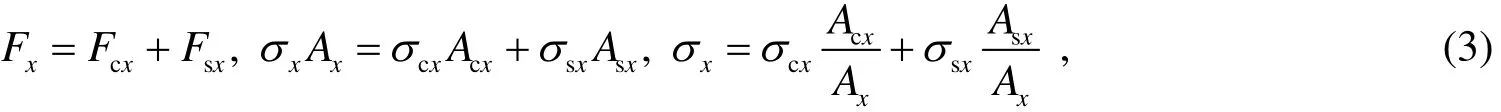
式中: Fcx为混凝土在x方向上所受荷载; Fsx为钢筋在x方向上所受荷载; σx为钢筋混凝土板应力; σcx为混凝土应力; σsx为钢筋应力。根据钢筋与混凝土之间的粘结假设与虎克定律:

对于x、y方向, 提供上式中3个参数中的2个即可计算得出第3个参数的值。由于本文所采用的是钢筋混凝土板, z方向的厚度远小于x、y方向的跨度, 在z方向上钢筋对钢筋混凝土板的增强作用较弱, 取μz= μcz。对于x、y方向, 假设混凝土在x方向受拉, 产生的横向收缩变形量为 Δby= byεy= -byεxμxy,式中: by为代表性结构微元横向尺度; εy为代表性结构微元横向应变。

由基本假设知, 横向收缩变形为钢筋与混凝土横向收缩变形量之和, 即Δby= Δbcy+ Δbsy=-bcyεcxμcbsyεsxμs。式中: μs为钢筋泊松比; μc为混凝土泊松比。且εx= εcx= εsx, 因此有。

2 有限元建模与分析

2.1 实验数据提取

根据实验所采用四边固结矩形混凝土板[8], 提取参数为: 长4.5 m, 宽3.5 m, 厚100 mm; 混凝土密度25 kN/m3, 上板面承受4.5 kN/m2均布荷载; 钢筋与混凝土弹性模量分别为2.1 × 105和2.8 × 104N/mm2, 钢筋混凝土板的弹性模量为2.87 × 104N/mm2; 钢筋的泊松比为0.3, 混凝土的泊松比为0.2; 钢筋与混凝土的剪切模量分别为7.94 × 104N/mm2, 1.11 × 104N/mm2。x、y方向的配筋率分别为0.551%和0.433%。钢筋混凝土板在荷载与自重共同作用下板中最大挠度值为0.946 mm。

将以上数据代入各相关公式得弹性常数: Ex= 28 980 N/mm2, Ey= 28 766 N/mm2, Ez= 28 550 N/mm2;Gxy= 11 896 N/mm2, Gxz= 11 986 N/mm2, Gyz= 12 075 N/mm2; μxy= μyx≈ 0.2, μxz≈ 0.2, μyz≈ 0.2。

2.2 有限元建模与分析

随着计算机在数值模型方面的迅速发展, 出现了大量的有限元分析软件, 其中Ansys[9–10]就是一款大型通用的有限元(FEA)分析软件。Ansys15.0的主要三部分为前处理模块、分析计算模块和后处理模块。前处理模块提供了非常强大的实体建模以及网络划分工具, 在前处理阶段, 建立三维尺寸为4.5、3.5、0.1的板块结构, 采用各向异性单元Solid185, 在材料属性部分输入前文得到的正交各向异性材料的9个独立力学参数, 随即建立四边固结正交各向异性钢筋混凝土板有限元模型。对板四周施加固定约束后进行自由分网如图2所示。

图2 钢筋混凝土板有限元模型及分网

对板上表面施加向下均布荷载以及考虑板的自重, 通过有限元结构计算, 得到X、Y、Z各个方向上的应力及应变情况分别如图3、图4所示。

图3 正交各向异性材料各方向应力

图4 正交各向异性材料各方向应变

为获取钢筋混凝土板在受力方向上的挠度, 通过Ansys后处理工具显示受力方向, 即Z方向上的位移挠度如图5所示, 其中最大挠度值为0.981 mm。

图5 正交各向异性混凝土板Z方向挠度

为了与考虑钢筋混凝土板为各向同性时的情况进行比较,建立各向同性钢筋混凝土板有限元模型。取各向同性有限元单元Solid65[11], 将钢筋混凝土板的弹性模量与泊松比作为参数进行有限元模拟分析, 得到各向同性钢筋混凝土板各方向的应力及应变以及Z方向的挠度值分别如图6～8所示。最大挠度值为1.012 mm。为直观地比较2种情况下混凝土板的应力、应变及位移挠度, 提取各向同性以及各向异性情况下的钢筋混凝土板的各方向应力、应变值如表1所示。

图6 各向同性材料各方向应力

图7 各向同性材料各方向应变

通过对钢筋混凝土板分别在各向同性与正交各向异性的情况下的有限元应力、应变分析(表1), 可以发现:在不考虑钢筋混凝土板的正交各向异性时, 在板自重与均布荷载作用下的板中挠度为1.012 mm;在考虑钢筋混凝土板的正交各向异性时, 其板中挠度为0.981 mm, 较前者减少了3.23%。2种情况下的应力及应变值基本接近。

图8 各向同性混凝土板Z方向挠度

表1 各向同性与正交各向异性材料应力及应变

3 结论

本文对正交各向异性材料的应力及应变本构关系进行了推导。并将钢筋配筋率作为影响钢筋混凝土板弹性模量的因素, 结合有限元建模及其分析方法, 计算与分析了正交各向异性板的应力、应变关系及力学参数, 得到以下结论。

(1) 钢筋对混凝土板的增强效果通过配筋率体现, 使得钢筋混凝土作为复合材料来计算其各项力学参数。提取计算正交各向异性材料所需的9个独立参数, 对正交各向异性钢筋混凝土板的应力、应变进行有效地有限元分析, 得到了各个方向的应力、应变及非约束向的挠度值。

(2) 分别考虑在材料的各向同性与正交各向异性的情况下, 钢筋混凝土板承受均布荷载, 得到了各个方向的应力、应变以及板中挠度。其中, 当视材料为各向同性时, 其应力、应变及板中挠度均大于视材料为正交各向异性的情况, 差别幅度不大。2种情况下的有限元模拟分析所得挠度值均大于实验值,且较实验值的差别幅度在7%以内, 说明本文所采用的有限元分析方法具有实质意义。

(3) 根据实验的裂缝情况, 本文假设钢筋混凝土板在受力方向上的刚度保持不变, 未考虑混凝土应力重分布对钢筋混凝土板的应力、应变产生的影响, 虽此假设不影响正交各向异性混凝土板与各向同性混凝土板的应力、应变分析比较, 但由此假设所产生的具体量化影响还有待进一步考察。

(4) 由于有限元分析软件的广泛应用, 本文所做的各向同性与正交各向异性的钢筋混凝土板的应力、应变分析结果为分析各向异性材料的力学性能提供了简化思路。视材料为各向同性时的应力、应变均大于视材料为正交各向异性时的应力、应变, 若在混凝土结构设计中考虑该因素, 工程会更偏向于安全。

[1] 谭继锦. 正交各向异性材料应力应变关系的表述形式[J]. 力学与实践, 1991, 13(2): 64–65.

[2] 郑晓霞, 郑锡涛, 缑林虎. 多尺度方法在复合材料力学分析中的研究进展[J]. 力学进展, 2010, 40(1): 40–55.

[3] 程选生, 杜永峰. 正交各向异性钢筋混凝土板结构弹性常数的确定[J]. 四川建筑科学研究, 2006, 32(5): 30–33.

[4] 花宏伟, 彭皖生. 现浇钢筋混凝土楼板裂缝的成因及防治措施[J]. 治淮, 2015(6): 47–48.

[5] 闫晓荣, 林皋. 基于混凝土应力—应变关系的正交各向异性损伤模型及其应用[J]. 水科学与工程技术, 2005(4):39–43.

[6] 吴晓, 罗佑新. 剪切变形对双模量梁弯曲正应力的影响[J]. 湖南文理学院学报(自然科学版), 2016, 28(1): 55–59.

[7] 刘锡礼, 王秉权. 复合材料力学基础[M]. 北京: 中国建筑工业出版社, 1984: 37–55.

[8] GB50010-2002, 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2002.

[9] 朱伯芳. 有限单元法原理与应用[M]. 3版. 北京: 中国水利水电出版社, 2009: 192–213.

[10] Balomenos G P, Genikomsou A S, Polak M A, et al. Efficient method for probabilistic finite element analysis with application to reinforced concrete slabs [J]. Engineering Structures, 2015, 103: 85–101.

[11] 刘琴, 马石城, 印长俊. 钢纤维混凝土弹性模量在有限元数值模拟中的实现[J]. 湖南文理学院学报(自然科学版),2014, 26(4): 35–38.

(责任编校: 江河)

Analysis of stress and strain about orthotropic steel reinforced concrete slab

Zhong Hao, Yin Changjun, Fang Honghua
(School of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105, China)

For the research of orthotropic material stress strain relationship and the mechanical parameters such as elastic modulus, starting from the physical and mechanical properties of materials, the equations of the elastic orthotropic material constitutive equation are put forward. The orthogonal anisotropy of reinforced concrete plate under dead weight and the loading of stress-strain relationship and plate deflection value are simulated by finite element analysis software. Also, the reinforced concrete slab as isotropic stress and the strain of the situation are contrasted. It is found out that two cases of stress strain relationship and deflection values with the experimental data are close to the plate, so it is feasible. According to the results of the two cases of similar simulation, it provides a simplified way of thinking.

orthotropic; reinforced concrete slab; stress and strain; FEA

TU 375.2

: A

1672–6146(2017)03–0054–05

10.3969/j.issn.1672–6146.2017.03.012

钟浩, 53790310@qq.com。

: 2017–03–16