条形基础作用下加固边坡的抗震稳定性分析
2017-07-18王作伟黄诗阳
王作伟, 黄诗阳
(长沙市中等城乡建设职业技术学校, 湖南 长沙, 410216)
条形基础作用下加固边坡的抗震稳定性分析
王作伟, 黄诗阳
(长沙市中等城乡建设职业技术学校, 湖南 长沙, 410216)
边坡坡顶设有构筑物时, 其埋置于坡顶土体内部的条形基础将对边坡稳定性构成直接影响。借助极限分析上限原理, 对坡顶作用有条形基础的加固边坡的抗震稳定性进行了研究。基于对数螺旋曲线破坏模式,通过各项功率的确定, 获得了边坡抗震安全系数的表达式。通过参数优化分析了条形基础尺寸、土体强度非线性和地震荷载等因素对边坡稳定性和潜在滑移范围的影响。分析结果表明: 抗滑桩最佳支护位置不因土体强度参数的改变而发生变化; 条形基础尺寸、地震荷载和土体强度非线性等因素均对边坡稳定性影响显著。
边坡稳定性; 条形基础; 上限法; 土体非线性; 抗震稳定性
在边坡上进行构筑物建设是一种有效的山区地形利用手段。边坡坡顶的开挖和建筑物基础的埋设将对此类边坡建设的稳定性形成不利影响。进行工程设计和施工时, 为确保边坡稳定性与其使用功能良好,《建筑地基基础设计规范》[1]指出基础边界距坡顶一侧边界的水平距离(B)、边坡坡度(β)、基础的埋深(d)和宽度(b)应满足关系式B≥3.5b–d/tanβ。除该式中包含的影响因素外, 边坡稳定性还直接与其土体强度以及外界失稳诱因有关。当坡顶受荷较大且受到地震荷载等的作用时, 边坡强度降低, 难以满足工程要求。此时, 必须采取抗滑桩加固等手段提高其稳定性。极限平衡法、有限元法和极限分析法[2–6]是岩土工程稳定性分析的常用方法。其中极限分析法由于其广泛的适用条件和良好的分析效果, 在边坡稳定性分析中应用较多[7]。Chen[8]系统地将极限分析方法引入到岩土工程稳定性分析中, 并分别对边坡稳定性、地基承载力以及挡土墙边坡主、被动土压力问题进行了研究。通过对破坏准则的合理修正, 杨小礼[9]将Chen[8]的工作推广到非线性条件。Michalowski[10]构建了三维边坡的曲线圆锥破坏模式, 通过优化计算将三维边坡稳定性分析结果与二维结果进行了对比, 验证了破坏模式的合理性。高玉峰等[11]在Michalowski[10]工作的基础上, 将三维边坡破坏模式拓展到趾前破坏、坡趾破坏和趾后破坏3种, 并分别进行了稳定性研究。借助曲线拟合手段, Saada[12]等采用极限分析有限元方法对渗流作用下岩质边坡稳定性进行了分析。在边坡加固方面, Michalowski[13]和高玉峰等[14]分别在二维和三维条件下从筋材的最小加筋强度和长度两方面对加筋土边坡的稳定性进行了研究。文畅平[15]就锚杆支护边坡的抗震问题从试验和理论分析方面进行了系统论述。
本文基于极限分析上限法, 对坡顶埋设有条形基础的加固边坡进行了稳定性研究。通过构建边坡破坏机构, 计算各项功率, 获得边坡安全系数的解析式。借助参数优化分析了各因素对安全系数和潜在破坏范围的影响。
2 极限分析上限法和非线性Mohr-Coulomb破坏准则
2.1 极限分析上限法
极限分析方法是岩土工程中应用最为广泛的分析方法之一, 由上限法与下限法组成。在边坡工程方面, 应用上限法的首要条件在于边坡破坏模式和相容速度场的确立。通过确定各部分的能量耗散, 基于虚功原理可获得表征边坡稳定性的极限状态能量方程, 即, 其中,Wext和Dint分别为临界破坏机构对应的总外力功率和内能耗散总量。
2.2 非线性Mohr-Coulomb破坏准则
线性Mohr-Coulomb准则采用黏聚力c和内摩擦角φ两个参数对土体强度进行描述。然而, 非线性Mohr-Coulomb准则强度包络线为一条曲线, 无法直接获得其斜率与坐标系纵轴上的截距。因此, 杨小礼等提出了适用于非线性Mohr-Coulomb准则的切线法, 即过强度包络线上的任意一点作切线(图1),并采用该切线的纵轴截距ct和斜率tanφt表示土体黏聚力和内摩擦角。该切线方程表达式为

其中, ct和tanφt分别为切线的纵轴截距与斜率。

图1 非线性Mohr-Coulomb破坏准则及其切线
通过图1和式(1), 可得截距ct的表达式为。其中, m为非线性系数, c0为初始黏聚力。在采用切线法进行优化分析时, φt将被视为一个自变量带入到各式中。
3 边坡破坏模式
3.1 未加固边坡破坏模式
条形基础作用于坡顶的未加固边坡破坏模式如图2所示。点O为潜在滑移面 AB的旋转中心, 边坡坡角和坡高分别为β和H, 坡顶宽度和潜在滑移面终点B距坡趾点C的距离分别为L和D,q为宽度为b的条形基础施加于坡顶土体的均布荷载, 该基础左缘距边坡坡顶左端点D的距离为B, 埋深为d。θ0和θh为描述边坡破坏范围的角度, g和kh分别为重力加速度和横向地震荷载系数。

图2 桩基础作用于坡顶的边坡破坏模
3.2 抗滑桩加固的边坡破坏模式
实际工程中, 自然状态下的边坡往往需要通过人工支护的手段满足其工程使用要求, 本文的计算中采用抗滑桩加固的边坡支护方法(图3)。抗滑桩距坡趾C点的水平距离和有效加固长度分别为XF和h,其他与抗滑桩有关的参数见下文中抗滑桩能耗计算部分。
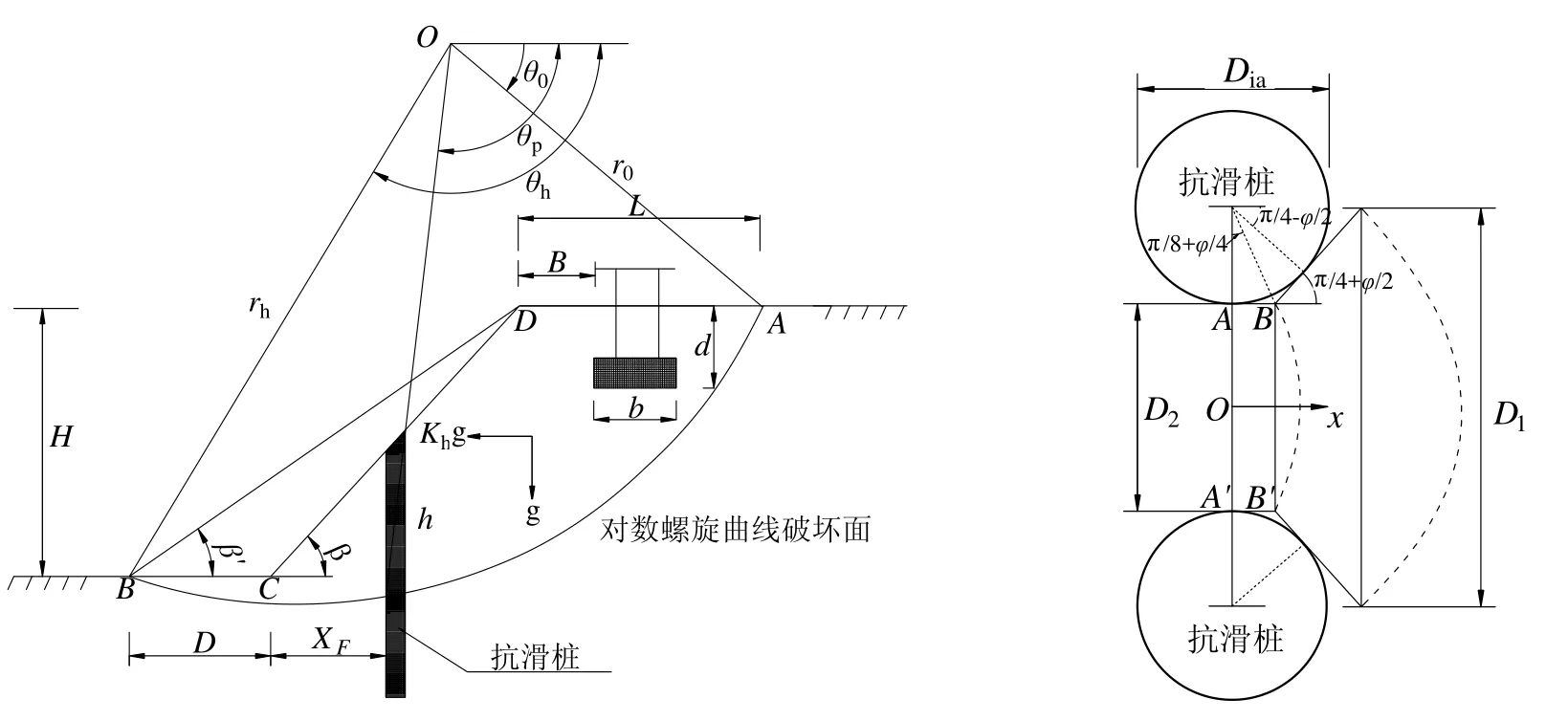
图3 桩基础作用于坡顶的抗滑桩加固边坡
4 能耗计算与目标函数优化求解
4.1 无加固措施的边坡能耗计算
不考虑抗滑桩作用时, 本文破坏模式中的功率由土体重力功率、地震荷载功率和边坡坡顶基础外力功率以及潜在滑动面上的内力功率组成。
根据图2中的几何关系, 通过叠加法获得土体重力功率的表达式为。其中:。
从以上计算可获得计算无加固措施边坡安全系数的各项外力和内部能量功率。本文计算中, 由于考虑了抗滑桩对边坡的加固效应, 因此需要借助图3所示的破坏机构对抗滑桩在边坡加固过程中的能量功率进行计算。
4.2 抗滑桩能耗计算如图3所示, 根据Ito[16]和Hassiotis等[17]的研究成果, 抗滑桩加固边坡时其提供的横向单位抗力为
进行抗滑桩功率计算时, 需要对单位抗力沿滑动面以上的抗滑桩长度进行积分, 再计算总的功率。其中,。
4.3 目标函数优化求解
为获得边坡安全系数的优化解, 根据本文破坏模式的几何关系获得优化过程的约束条件, 并在这些条件的约束下通过MATLAB软件寻找最优解, 本文中为合理的Fs最小解。约束条件为: 0 < θ0≤ θp≤ θh< π; 0 < h ≤ H; B < L; b < L。在该约束条件下, 可获得边坡安全系数的最小解, 并借此通过参数分析条形基础尺寸、抗滑桩布设位置和土体强度非线性等对边坡安全系数和潜在滑动面形状的影响。
5 参数分析与数值模拟
5.1 条形基础尺寸对边坡稳定性的影响
分别从边坡宽度b和左翼距离边坡坡顶左侧端点距离B两方面分析坡顶条形基础尺寸对边坡安全系数的影响规律。计算中, 取地震荷载系数kh= 0.1, 其他参数详见图4。从图4可见, 条形基础宽度的增大将对边坡稳定性产生不利影响, 而左翼距边坡坡顶左侧端点距离的增大, 使边坡稳定性提高, 此2参数在不同的边坡坡角β下, 对边坡安全系数的影响规律均近似线性; 此外, 当坡角不断增大时, 边坡的安全系数持续降低, 但坡角的改变不影响B或者b对安全系数的作用规律。

图4 坡顶条形基础尺寸对边坡稳定性的影响
5.2 抗滑桩布设位置对边坡抗震稳定性的影响
对边坡进行抗滑桩支护时, 最合理加固位置是一个必须要考虑的重要因素。为此, 分别选取尺寸为H = 15 m, β = 30°和H = 10 m, β = 45°两边坡进行抗滑桩支护效应分析, 其他参数见图5。从图5可见, 2图中边坡抗滑桩的最佳支护位置均处在XF/Lx= 0.7附近, 土体内摩擦角对抗滑桩支护效果影响显著, 但对最佳支护位置几乎无影响, 即无论土体强度参数如何, 其最佳支护位置保持不变。

图5 抗滑桩支护位置对边坡稳定性的影响
5.3 土体强度非线性及地震荷载对边坡抗震稳定性的影响
选取尺寸为H=15 m, β=30°进行土体强度非线性及地震荷载对边坡稳定性的影响分析, 其中土体强度非线性系数m取值为1.2~2.0, 地震荷载系数kh取值为0~0.3, 其他参数见图6。从图6可知, 边坡的安全系数随着地震荷载系数和非线性系数的增加而不断减小, 且安全系数随非线性系数m的增加而不断降低的速率亦持续降低。较之非线性系数、地震荷载系数对边坡安全系数的影响更为强烈, 当地震荷载从0增加到0.2时, 非线性系数m = 1.2、1.4、1.6和2.0对应的安全系数分别降低了41.2%、47.9%、58.6%和62.6%, 说明土体强度非线性越为强烈, 地震荷载对边坡计算安全系数的影响愈显著。

图6 土体强度非线性和地震荷载对边坡稳定性的影响
5.4 坡顶桩基础及土体强度非线性对边坡潜在滑动面的影响分析
通过参数优化计算获得反映边坡潜在滑动面尺寸的参数θ0、θh以及其他参数, 并绘制潜在滑动面图形如图7所示, 其中边坡高度H = 15 m, 坡角β = 45°。

图7 坡顶受荷及土体强度非线性对边坡潜在滑动面的影响
从图7(a)可知, 当边坡坡顶无条形基础作用且有抗滑桩支护时, 其潜在破坏面最浅, 滑移块体体积最小, 随着坡顶条形块体的增设和支护条件的缺失, 滑移面逐渐变深, 滑移块体体积不断增大。从图7(b)可知, 边坡潜在滑移面随着非线性系数的增大而不断加深, 破坏范围亦逐渐增大, 即土体的稳定性状态逐渐变差, 这也证实了前文中参数分析结果的有效性。
5.5 土体强度非线性对潜在滑移面影响的数值模拟分析
为验证本文计算结果的有效性, 借助FLAC3D有限差分软件对土体强度非线性对边坡潜在滑移面的影响进行研究。图8(a)和图8(b)中边坡高度H = 15 m、坡角β = 45°、非线性系数m分别为1.2和1.8。

图8 土体强度非线性对边坡潜在滑移面影响的数值模拟
从图8可见, 当土体强度非线性系数m从1.2增大到1.8时, 潜在滑移面从较为靠近坡面的位置深入到边坡内部, 边坡失稳范围显著增大, 说明土体强度非线性的增强将削弱边坡稳定性。同时, 通过与图7(b)中通过优化计算获得的边坡潜在滑移面的比较, 认为本文优化计算结果与数值模拟计算结果吻合程度良好, 验证了本文计算结果的有效性。
6 结论
借助极限分析上限法, 本文进行了坡顶作用有条形基础的边坡非线性抗震稳定性研究。通过对各项能量功率的计算获得边坡安全系数显式解答, 进而通过软件优化得到安全系数最优解。通过参数分析研究了坡顶条形基础尺寸、抗滑桩支护位置等对边坡稳定性的影响, 并借助FLAC3D数值模拟软件验证了本文计算结果的有效性。本文得到以下主要结论。
(1) 条形基础宽度的增加将对边坡稳定性产生不利影响, 而基础距坡顶左端点距离的增大会使边坡稳定性提高, 此2参数对边坡安全系数的影响规律均近似线性, 坡角变化并不影响此2因素对边坡稳定性的影响规律。
(2) 抗滑桩的最佳支护位置处在XF/Lx= 0.7附近, 土体内摩擦角对抗滑桩支护效果影响显著, 但对最佳支护位置无影响。
(3) 地震荷载系数和非线性系数均对边坡稳定性具有不利影响, 安全系数随着非线性系数的增加而不断降低, 且降低的速率持续减小。土体强度非线性越强烈, 地震荷载对边坡计算安全系数的影响愈为显著。
(4) 边坡坡顶受荷和支护情况对潜在破坏范围具有明显影响, 随着坡顶条形块体的增设和支护条件的缺失以及土体非线性的增强, 滑移面逐渐变深, 滑移块体积不断增大。
[1] GB 5007-2002, 建筑地基基础设计规范[S].
[2] 陈祖煜. 土质土坡稳定分析——原理 方法 程序[M]. 北京: 中国水利水电出版社, 2003: 67–72.
[3] 丁参军, 张林洪, 于国荣, 等. 边坡稳定性分析方法研究现状与趋势[J]. 水电能源科学, 2011(8): 112–114.
[4] 张常亮. 边坡稳定性三维极限平衡法研究[D]. 西安: 长安大学, 2008.
[5] 栾茂田, 武亚军, 年廷凯. 强度折减有限元法中边坡失稳的塑性区判据及其应用[J]. 防灾减灾工程学报, 2003, 23(3):1–8.
[6] 王水亮. 网格自适应有限元极限分析在边坡稳定分析中的应用[D]. 杨凌: 西北农林科技大学, 2015.
[7] 郑颖人. 岩土数值极限分析方法的发展与应用[J]. 岩石力学与工程学报, 2012, 31(7): 1 297–1 316.
[8] Chen W F. Limit analysis and soil plasticity [M]. Amsterdam: Elsevier Science, 1975: 381–403.
[9] 杨小礼. 线性与非线性破坏准则下岩土极限分析方法及其应用[D]. 长沙: 中南大学, 2002.
[10] Michalowski R L, Drescher A. Three-dimensional stability of slopes and excavations [J]. Géotechnique, 2009, 59(10):839–850.
[11] Gao Y F, Zhang F, Lei G H, et al. An extended limit analysis of three-dimensional slope stability [J]. Géotechnique, 2013,63(6): 518–524.
[12] Saada Z, Maghous S, Garnier D. Stability analysis of rock slopes subjected to seepage forces using the modified Hoek-Brown criterion [J]. International Journal of Rock Mechanics & Mining Sciences, 2012, 55: 45–54.
[13] Michalowski R L. Soil reinforcement for seismic design of geotechnical structures [J]. Computers & Geotechnics, 1998,23(1): 1–17.
[14] Gao Y, Yang S, Zhang F, et al. Three-dimensional reinforced slopes: Evaluation of required reinforcement strength and embedment length using limit analysis [J]. Geotextiles & Geomembranes, 2015, 44(2): 133–142.
[15] 文畅平. 多级支挡结构与边坡系统地震动力特性及抗震研究[D]. 长沙: 中南大学, 2013.
[16] Ito T, Matsui T. Design method for stabilizing piles against landslide-one row of piles [J]. Soil and Foundations, 1981,21(1): 21–37.
[17] Hassiotis S, Chameau J L, Gunaratne M. Design method for stabilization of slopes with piles [J]. Journal of Geotechnical& Geoenvironmental Engineering, 1999, 125(10): 910–914.
(责任编校: 江河)
Seismic stability analysis of strip foundation loaded slope reinforced by a row of piles
Wang Zuowei, Huang Shiyang
(Changsha Urban and Rural Construction College, Changsha 410216, China)
Strip foundation located on slope crest will significantly influence the stability of slope. Based on the limit analysis upper bound theorem, a nonlinear seismic stability analysis of slope with strip foundation on crest is conducted. Objective function is obtained by equaling the external works to the internal energy dissipation of the potential logarithm failure curve, then the optimal solution of the slope safety factors are obtained by parameter optimization. Parameter analysis of strip foundation shape, soil nonlinearity and seismic forces on slope stability as well as the sliding curve is taken place afterwards. The results show that the most suitable reinforcement location of piles on slope will not change no matter what the strength parameters are, at the same time, factors such as the strip foundation shape, the seismic forces and the soil nonlinearity all have significant effects on slope stability.
slope stability; stripe footing; upper bound theorem; soil nonlinearity; seismic stability
P 642.22
: A
1672–6146(2017)03–0088–07
10.3969/j.issn.1672–6146.2017.03.019
王作伟, 181807339@qq.com。
: 2017–03–25
