坡度对坡面降雨产流规律的影响

王 杰,王 妍,许晓梁,陈 力

(河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京 210098)

坡度对坡面降雨产流规律的影响

王 杰,王 妍,许晓梁,陈 力

(河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京 210098)

通过建立概化坡面模型,设置不同坡度下的单层无限深均质各向同性梯形壤土剖面,在不考虑蒸散发和土壤水分滞后效应的前提下,假定若干初始土壤含水量,借助Hydrus软件,在给定时空分布均匀降雨的条件下对Richards’方程进行数值计算以探索坡度对霍顿型降雨产流过程的影响。结果显示产流基本随坡度增加而减小,而初始土壤含水量增加将抑制坡度对产流的影响,用幂函数可以较好地近似产流和坡度之间的关系。

坡度;降雨产流;初始土壤含水量;Hydrus软件;数值计算

山坡降雨入渗在近一个世纪得到了极大的关注[1-2],其关系着众多的环境过程,如地表产流机制、土壤侵蚀、滑坡、泥石流以及对于基流的补给。许多研究者通过流域观测、室内试验、数值模拟等手段对山坡降雨入渗进行研究。Chaplot 等[3]在以粉壤土为主的巴黎盆地西北部的试验流域通过考虑恒定强度的人工降雨和自然降雨的方式研究了坡度2%～8%情况下的产流情况, 结果表明随着坡度的增加,产流出现增加的趋势,降雨强度增加,产流也会增加,并将这种现象归因于坡度增加导致坡面流速增加,从而可能使产流量增加。Sharma等[4]则在以壤沙土为主的印度沙漠通过6 a的降雨径流观测探索坡度和坡长对产流规律的影响,同样发现坡长对产流并无显著的影响,而坡度增加则产流显著增加,并将这个原因归结于土壤表面的结皮现象,坡度增加削减了降雨情况下的入渗时间。然而Posen[5]通过室内试验,在恒定强度的人工降雨条件下探索5种坡度下的产流规律,发现坡度增加导致产流减小,认为坡度增加,片状侵蚀和细沟侵蚀相应地增加或者土壤表层被相应地稀释,从而导致产流减小。而Lal[6]认为坡度对产流并无明显影响。Chen等[7]通过修改Green-ampt模型数值模拟,考虑在土壤各向同性均匀、降雨稳定的情况下不同坡度对产流结果的影响,结果表明在一定的降雨条件下产流随坡度增加而减小,但当降雨增加到一定程度时,在一定范围内坡度对产流影响并不明显。但是由于不同的研究者所用方法、考虑因素等存在差异,关于坡度对降雨产流过程的影响得到的结论也有所不同。实际上,无论是试验还是数值模拟,由于降雨时空、下垫面分布难以均匀、降雨对坡面存在各种各样的侵蚀,和在某种程度上由于降雨形成结皮抑制下渗等各种差异,以及数值计算存在精简可能无法完全反映坡面降雨产流规律等,坡面降雨产流规律并未真正明晰。笔者拟通过建立概化坡面模型,利用Hydrus软件对Richards’ 方程进行数值计算,进一步探索不同坡度下的降雨产流规律,旨在为坡面水文模型的发展、污染物运移等提供参考。

1 坡面降雨产流模型

1.1 笛卡尔坐标系下的降雨产流

假定土壤为多孔介质,对于笛卡尔坐标系,取向上和向右的方向作为正方向,则非饱和或变饱和土壤水分运动可用Richards’方程表述:

(1)

式中:h——压力水头(在非饱和土壤中表示基质势,在饱和土壤中表示静水压力势),mm;θ(h)——土壤含水量(表示为h的函数),无量纲;t——时间,h;·——散度符号;——梯度符号；K(h)——土壤水力传导度(表示为h的函数),mm/h;z——二维笛卡尔坐标系坐标(另一个为x),mm。

为求解式(1),需要引入描述土壤含水量与压力水头关系和水力传导度与压力水头关系的方程,即土壤水分特征曲线和水力传导度函数。土壤水分特征曲线用van Genuchten[8-9]方程描述:

(2)

对应于van Genuchten方程,土壤水力传导度函数使用Mualem公式[9],表示为

(3)

式中:θr——残余土壤含水量(体积含水量,下同),无量纲;θs——饱和含水量,无量纲;α、m、n——经验参数(其中m和n满足一定的关系:m=1-1/n,n>1);l——土壤的空隙连同系数,对于绝大多数土壤,其取值为0.5;Ks——饱和水力传导度,mm/h。

对于下渗率,其计算模式如下[9]:

(4)

累积下渗深度可按下式进行计算:

(5)

如果对于给定的降雨总量,那么累积地表径流深为

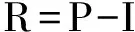
(6)

式中:i——水平面上的下渗率(表示为时间t的函数),mm/h;z*——坡面符号；I——水平面上的累积入渗量,mm;R——累积地表径流深,mm;P——累积降雨量,mm。

1.2 坡面模型概化

自然界中,平坦的坡形很少存在,大多是以凹凸不平的形态出现,而且总是与水平面有一定的夹角(γ),即山坡。为了研究方便,以梯形的土壤剖面近似为原型(图1),并假定这个梯形土壤剖面为半无限深的均匀各向同性土柱。自然界的完整山坡,左右边界往往都是无水分交换的,因此左右边界设为无流动的边界。降雨落在坡面上,一部分下渗,另一部分以产流的形式流出坡面,该部分边界属于与大气直接接触的边界,为大气边界。然而,由于土柱半无限深,为保证土壤水分运动的连续性,下边界概化为自由下渗边界。假定落在坡面上的降雨在时间和空间上分布都是均匀的,且在降雨的初始时刻,分布在整个土壤剖面的含水量是均匀的,任意两点之间不存在任何的压力梯度。为适应不同坡度的变化,对左右边界之间的水平距离(即下边界长度)予以固定,通过调整梯形土壤剖面左顶点的位置以适应不同位置坡度的改变。在这里,考虑下边界长度为50 m,右边界固定,高6 m。

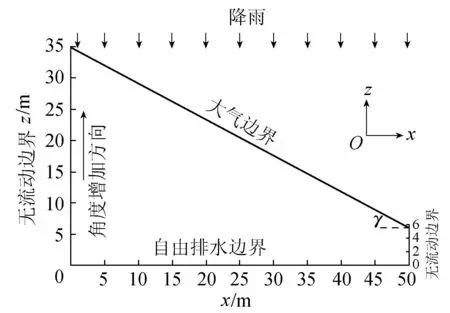
图1 坡面降雨产流模型概化Fig.1 Simplified model for rainfall-runoff generation on slope

1.3 数值模拟方法[7]

有限元软件Hydrus在数值求解 Richards’ 方程方面已得到广泛的验证和应用[9-10]。这里考虑的坡度范围为0°～60°,每间隔5°划分为一类,共计13种土壤剖面形态,土壤以壤质土为例,其对应于式(2)和式(3)的参数[8]取值为:θr=0.078,θs=0.43,α=0.003 6 mm-1,n=1.56,Ks=10.4 mm/h,l=0.5。考虑初始土壤含水量在剖面各个点相同,分别为0.2和0.3,代表该土壤相对较干和相对较湿的情况,设定总降雨量为90 mm,降雨强度(记为Pr)分别为15 mm/h、20 mm/h、25 mm/h、30 mm/h。

Hydrus对于概化坡面计算模型的边界具体处理为:对应自由下渗边界,假定地下水位远离模拟区域,即半无限深土柱,采用第二类边界的梯度边界描述,即

(7)

式中:g0——规定的总梯度, 具体参考文献[7]。

对于大气边界,采用的是Neuman提供的方法[9]:

(8)

(9)

式中:E——当前大气状况下最大的潜在下渗率,mm/h;hA、hs——在当前土壤状况下最小和最大的压力水头(见文献[9]),mm。

当满足不等式(8)时,规定的水头边界公式(式(4))将用于计算实时的下渗率。而对于无流动边界,根据第二类边界进行描述:

(10)

对于初始土壤含水量,Hydrus采用以下公式进行计算:

(11)

式中:θ0——指定的初始土壤含水量,与位置相关,无量纲。

为了提高精度,Hydrus在数值计算过程中需要建立网格并不断对网格实现剖分,水量平衡误差和坡面下渗曲线将作为衡量数值仿真好坏的标准。

2 结 果 分 析

利用Hydrus 2D/3D建立概化坡面模型进行数值计算,通过三角网不断细化剖分,在计算结果变化不大和保证水量平衡的前提下,通过提取处理,获得初始土壤含水量分别为0.2和0.3时不同降雨强度下产流随坡度的变化关系(图2)。

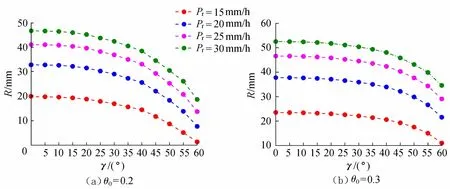
图2 不同初始土壤含水量时各降雨强度产流随坡度的变化关系Fig.2 Relationship between runoff and slope gradients for different rainfall intensities with different initial soil water contents

从图2可以看出,在相同的初始土壤含水量和相同的降雨强度下,坡度增加,产流减小,这种规律在降雨强度小土壤含水量低时,规律特别明显。对应于相同的坡度,随着降雨强度的均匀增加,相同初始土壤含水量的土壤总产流差异趋于减小。在相同的初始土壤含水量和同等坡度下,随着降雨强度增加,产流亦增加,当降雨量增大到一定程度时总产流量将趋于稳定。在降雨强度和坡度相同的情况下,初始土壤含水量增加,产流增加,当初始含水量达到饱和含水量时产流达到最大,这与文献[11-12]的结果相一致。在初始土壤含水量为0.2时,相邻降雨强度间,随着坡度的增加,产流的差异趋于减小;在初始土壤含水量为0.3时也表现出相同的规律。此外,在相同的初始土壤含水量条件下,随着降雨强度的增加,相邻坡度的产流差异不断减小。以初始土壤含水量为0.2为例,当其他坡度斜坡与平坡的产流相对误差不超过5%时,认为该坡度对产流的影响可以忽略不计。对于15 mm/h的降雨,坡度在15°以内的可以忽略其对产流的影响;但当降雨强度增加到20 mm/h时,坡度在20°以内的可忽略其对产流的影响;降雨强度为25 mm/h时,坡度在20°以内可以忽略其影响;降雨强度为30 mm/h时,坡度在20°以内可以忽略其影响。随着降雨强度的增加,忽略坡度对产流影响的临界坡度缓慢增加,大体而言,坡度小于15°时完全可以忽略降雨对产流的影响。但是,当初始土壤含水量增加到0.3时,降雨强度为15 mm/h的临界坡度为25°,而当降雨强度为20 mm/h、25 mm/h、30 mm/h时临界坡度延展至30°,初始土壤含水量的增加明显抑制了坡度对产流的影响。

Chen等[7,13]通过修改平面上的格林安普特模型获得坡面上的格林安普特模型,并得到如下结果:当降雨强度较小时,随着坡度的增加,产流量不断地减小,当降雨强度达到一定程度时,出现产流对坡度增加而表现出不明显地减小现象。该结果与本文得到的结论基本一致。从图2中不同降雨强度下的累积地表径流深和坡度曲线可以看出两者在某种程度上符合幂函数关系,借用Matlab软件对其进行回归分析,结果见表1、表2。

表1 初始土壤含水量为0.2时不同降雨强度下累积地表径流深与坡度回归分析结果

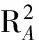
表2 初始土壤含水量为0.3时不同降雨强度下累积地表径流深与坡度回归分析结果

从表1和表2可以看出累积产流量与坡度关系拟合很好,并通过了相关性检验。相对于线性回归[14]和抛物线[15],幂函数可以较好地模拟径流深与坡度的函数关系。由表1可知,回归公式幂数项指数近似为1,可以近似认为累积产流深与坡度余弦一次方成反比,随着降雨强度的增加,幂数项系数负增加,常数项系数增加,但幂数项指数相对稳定;相反,从表2可以看出回归公式幂数项指数近似为2,可以近似认为累积产流深与坡度余弦的二次方成反比,常数项近似等于降雨历时内按照稳定下渗率下渗所得累积产流量。此外,当降雨强度增加时,回归公式的幂数项系数减小,而幂数项指数和常数项增大。表1与表2结果差异较大,从表1和表2的常数项可以判断,差异的原因主要如下:初始土壤含水量较高时,累积径流深主要受稳定下渗率控制,大部分属于蓄满产流过程;而初始土壤含水量较低时,累积径流深主要受降雨强度控制,大部分属于超渗产流过程。回归公式各项系数受初始土壤含水量和降雨强度影响。

3 结 语

通过概化坡面模型,基于均一各向同性壤质土,在初始土壤含水量沿剖面分布均匀,并忽略蒸发和滞后效应的情况下,借助Hydrus软件对稳定性降雨条件下的霍顿型坡面入渗产流过程进行数值计算,得到以下规律:(a)在相同的降雨条件下,随着坡度的增加,坡面产流减小或者保持不变。降雨强度增大,相同坡度的坡面产流增加,而坡面产流相同的坡度逐渐从低坡度向高坡度拓展;初始土壤含水量增大,相同坡度坡面产流也增加,但是一定程度上抑制了坡度对坡面产流的影响,其影响范围延伸到较高的坡度上。(b)通过回归分析,累积坡面产流与坡度的关系可以用幂函数进行描述,以上结果可为山坡水文模型发展提供参考。

[ 1 ] KIRKBY M J.Hillslope hydrology[M].New York: John Wiley,1978.

[ 2 ] PHILIP J R.Hillslope infiltration: Planar slopes[J].Water Resources Research,1991,27(1):109-117.

[ 3 ] CHAPLOT V,BISSONNAIS Y L.Field measurements of interrill erosion under different slopes and plot sizes[J].Earth Surface Processes & Landforms,2000,25(2):145-153.

[ 4 ] SHARMA K,SINGH H,PAREEK O.Rainwater infiltration into a bare loamy sand[J].Hydrological Sciences Journal,1983,28(28):417-424.

[ 5 ] POSEN J W.The influence of slope angle on infiltration rate and Hortonian overland flow[J].Geomorphology,1984,49(2):117-131.

[ 6 ] LAL R.Soil erosion on Alfisols in Western Nigeria: Ⅱ.effects of mulch rates[J].Geoderma,1976,16(5):377-387.

[ 7 ] CHEN Li,YOUNG M H.Green-Ampt infiltration model for sloping surfaces[J].Water Resources Research,2006,42(7):887-896.

[ 8 ] VOGEL T,van GENUCHTEN M T,CISLEROVA M.Effect of the shape of the soil hydraulic functions near saturation on variably-saturated flow predictions[J].Advances in Water Resources,2000,24(2):133-144.

[ 9 ] RADCLIFFE D E,IMÅNEK,J.Soil physics with HYDRUS: modeling and applications[M].London: CRC,2010.

[10] 左海军,张奇,徐力刚,等.基于数值模拟的土壤水渗漏对降雨条件的响应[J].水土保持学报,2009,23(1):31-35.(ZUO Haijun,ZHANG Qi,XU Ligang,et al.Numerical investigation on response of soil water percolation to rainfall condition[J].Journal of Soil and Water Conservation,2009,23(1):31-35.(in Chinese))

[11] 宋孝玉,白鹏,王娟,等.陕北黄土坡地枣园降雨入渗产流试验与模拟[J].西北农林科技大学学报(自然科学版),2014,42(11):163-168.(SONG Xiaoyu,BAI Peng,WANG Juan,et al.Experiment and simulation of rainfall infiltration and runoff in jujube orchard on loess slope filed of Northern Shaanxi[J].Journal of Northwest A & F University(Natural Science Edition),2014,42(11):163-168.(in Chinese))

[12] 李叶,吴玉柏,俞双恩,等.坡度对扰动黄棕壤土壤侵蚀的影响[J].河海大学学报(自然科学版),2016,44(1):20-24.(LI Ye,WU Yubai,YU Shuangen,et al.Influence of slope on disturbed yellow-brown soil erosion[J].Journal of Hohai University(Natural Sciences),2016,44(1):20-24.(in Chinese))

[13] 陈力,刘青泉,李家春.坡面降雨入渗产流规律的数值模拟研究[J].泥沙研究,2001,29(4):61-67.(CHEN Li,LIU Qingquan,LI Jiachun.Study on the runoff generation process on the slope with numerical method[J].Journal of Sediment Research,2001,29(4): 61-67.(in Chinese))

[14] 朱永杰,毕华兴,霍云梅,等.坡度与降降雨强度度对狗牙根草地产流的影响[J].中国水土保持科学,2015,13(6):20-25.(ZHU Yongjie,BI Huaxing,HUO Yunmei,et al.Effects of slope and rainfall intensity on runoff of Cynodon dactylon lawn[J].Science of Soil and Water Conservation,2015,13(6):20-25.(in Chinese))

[15] 王占礼,黄新会,张振国,等.黄土裸坡降雨产流过程试验研究[J].水土保持通报,2005,25(4):1-4.(WANG Zhanli,HUANG Xinhui,ZHANG Zhenguo,et al.Experimental study of runoff processes on bare loess hillslope[J].Bulletin of Soil and Water Conservation,2005,25(4):1-4.(in Chinese))

Effects of slope gradient on rainfall-runoff generation process

WANG Jie, WANG Yan, XU Xiaoliang, CHEN Li

(StateKeyLaboratoryofHydrology-WaterResourcesandHydraulicEngineering,HohaiUniversity,Nanjing210098,China)

Under the conditions of no evapotranspiration and soil water hysteresis, a simplified slope model was established for single-layer homogeneous and isotropic soil profiles on a trapezoid slope with infinite depth for different initial water contents. The Hydrus software, which was used to numerically solve Richards’ equation, was used to investigate the effects of slope gradients on the Horton runoff generation process during temporally and spatially uniform rainfall events. The results show that the runoff on the slope decreases with increasing slope gradients; increasing initial water contents may reduce the influence of slope gradients on runoff; and the relationship between runoff and slope gradients can be well approximated using power functions.

slope gradient; rainfall-runoff generation; initial water content in soil; Hydrus software; numerical calculation

10.3876/j.issn.1000-1980.2017.04.014

2016-08-15

王杰(1992—),男,湖北十堰人，硕士研究生,主要从事坡面水文物理规律模拟研究。E-mail: zmxxhy@qq.com

陈力,教授。E-mail: lchen@hhu.edu.cn

TU122

A

1000-1980(2017)04-0372-05