弱透水层释水过程中水力参数响应规律

李兆峰,周志芳,李明远,周翠英

(1.中山大学工学院,广东 广州 510275; 2.中山大学岩土工程和信息技术研究中心,广东 广州 510275; 3.河海大学地球科学与工程学院,江苏 南京 211100)

弱透水层释水过程中水力参数响应规律

李兆峰1,2,3,周志芳3,李明远3,周翠英1,2

(1.中山大学工学院,广东 广州 510275; 2.中山大学岩土工程和信息技术研究中心,广东 广州 510275; 3.河海大学地球科学与工程学院,江苏 南京 211100)

为了提高地下水运移模拟、地下水资源评价和地面沉降预测的精度,利用室内试验分析弱透水层释水固结过程中水力参数的变化规律。基于相邻含水层降深恒定且初始时刻水流稳定条件下弱透水层释水量的解析解,提出参数求解的配线法,利用研制的试验装置进行试验研究。结果表明:弱透水层释水过程中渗透系数和贮水率逐渐减小,固结系数变化不大。试验中土层的渗透系数和贮水率分别减小了52%和59%。弱透水层水力参数恒定不变的假设会对其释水量的计算造成较大误差,取弱透水层固结变形初始阶段的贮水率,计算结果比实际释水量大;取固结变形结束阶段的贮水率时则相反。

弱透水层;解析解;释水量;水力参数;滞后因子

地下水资源是人类淡水资源的重要组成部分,主要储存在含水层和弱透水层组成的含水层系统中[1]。弱透水层作为含水层系统的重要组成部分,在地下水资源管理和预测中经常被忽视[2-3]。弱透水层在冲积平原和沉积盆地中分布广泛,且主要由黏土、亚黏土、粉质黏土等细粒沉积物组成,具有低渗透性和高储水性[4-7]。弱透水层的渗透系数一般小于10-8m/s,比含水层小几个数量级[8-10],对地下水环境保护具有重要作用[11]。当抽水含水层水位下降时,弱透水层内部水压力减小,有效应力增加,弱透水层固结变形并释水到抽水含水层[12-13]。由于弱透水层的贮水率比含水层大1～2个数量级,弱透水层释水量相当大,弱透水层释水量的计算对于地下水资源评价极其重要[1-2]。弱透水层参数是其释水量计算的重要影响因素,因此弱透水层水力参数的确定是含水层系统水流运移模拟、地下水资源评价和地面沉降预测的关键。

弱透水层的水力参数包括渗透系数和贮水率,Field[14]指出固结系数的不确定性是传统固结理论计算变形速率的极限性。很多水文地质学研究者对弱透水层水文地质参数进行了大量研究.[15-16]。余闯等[17]推导出正常固结和超固结状态下固结系数与有效应力之间的表达式;张明等[18]利用统计分析得到固结系数与有效应力的拟合关系。上述研究主要针对软土的固结系数进行分析。叶淑君等[19]利用图解法对上海含水层系统中的弱透水层参数进行研究。Zhou等[20]提出了配线法求解弱透水层的渗透系数和贮水率,并通过室内试验验证了方法的可靠性。弱透水层释水过程中水力参数变化规律的研究尚未发现,特别是弱透水层的贮水率。笔者在Terzaghi固结理论的基础上推导了弱透水层定降深条件下释水量的解析解,利用该解析解提出相应条件下求解弱透水层参数的配线法,并通过室内试验对弱透水层释水过程中水力参数的响应规律进行研究。

1 原 理

图1 含水层系统概念模型Fig.1 Conceptual model of aquifer system

Terzaghi一维固结理论在解决软土地基变形控制和预测中发挥着重要作用,至今仍被广泛应用于计算各种荷载条件下土体的固结问题。为了研究弱透水层释水过程中水力参数的响应规律,建立了一个含水层系统概念模型,如图1所示。假设:(a)弱透水层是均质的,且渗透系数和贮水率不随时间变化;(b)弱透水层水平侧向无限延伸;(c)弱透水层始终是饱和状态;(d)弱透水层中的水流为垂向一维流,且服从达西定律。通常情况下弱透水层的渗透系数比含水层小两个数量级以上,因此,弱透水层中的水流可近似为一维流动。坐标轴原点O位于弱透水层的上表面,厚度为l,坐标z向下为正。

弱透水层的水压力用降深(s)代替,根据Terzaghi一维固结理论[21]建立数学模型:

(1)

式中:cv——土样的固结系数或者水力扩散系数;K、Ss——弱透水层的渗透系数和贮水率;t——时间。

初始时刻弱透水层内部水头线性分布,即其内部水流是稳定流。

(2)

式中:φ0——抽水含水层初始时刻的降深。

假设弱透水层上部含水层水位不变,即上边界降深为0,t时刻下部含水层降深增加量为φ,则

(3)

式(1)～(3)所示的偏微分方程,利用分离变量法可以求得其解析解[22]。

(4)

根据Darcy定律,求得弱透水层底面的水流速度,并进行无量纲化得

(5)

将式(5)取对数得

(6)

(7)

(8)

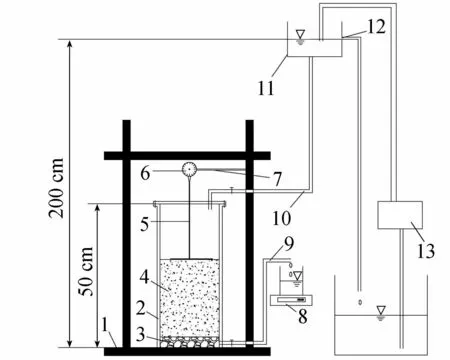
1—底座;2—容器主体;3—反滤层;4—黏土层;5—刚性杆;6—百分表;7—支架; 8—电子天平;9 —出水管;10—进水管;11—定水头供水槽;12—溢水口;13—蠕动泵图2 试验模型示意图Fig.2 Sketch of experimental model

2 试验结果及讨论

本文使用的试验装置是在前人试验模型的基础上进行改进,并尽量设计符合弱透水层固结渗流环境,模拟相邻含水层定降深条件下弱透水层释水过程中的水流运移问题。模型由模型主体(内径19.1 cm)、沉降量测系统、流量监测系统、供水水槽组成(图2)。为了研究弱透水层释水过程中水力参数的响应规律,对同一个土层不同定降深条件下弱透水层的释水规律进行了研究,其中土层的下边界降深(即相邻含水层的降深)逐渐变大(当降深变大时,确保上一次定降深试验土层内部水流已达到稳定)。随着土层下边界降深增大,土层释水量变大,根据试验过程中土层下边界流量,利用配线法计算土层水力参数,分析参数的变化规律。

试验所用土样是从野外取回的粉质黏土,将其风干、碾碎并过筛(0.5 mm)。将制备的土样填充到试验设备的主体部分,试验土样初始时刻厚度l=30 cm。试验初始时刻定降深ΔH=30 cm,待流量达到稳定时,此过程视为第一次定降深条件下的弱透水层水流运移试验结束;然后将出水口降低30 cm,进行第二次定降深条件下的弱透水层水流运移试验,待流量达到稳定时,第二次试验结束;依次进行5次试验至ΔH=150 cm。利用环刀法测得试验土层的基本性质,黏性土的干密度为1.14×103kg/m3,土的初始孔隙比e0=1.07。

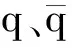
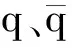
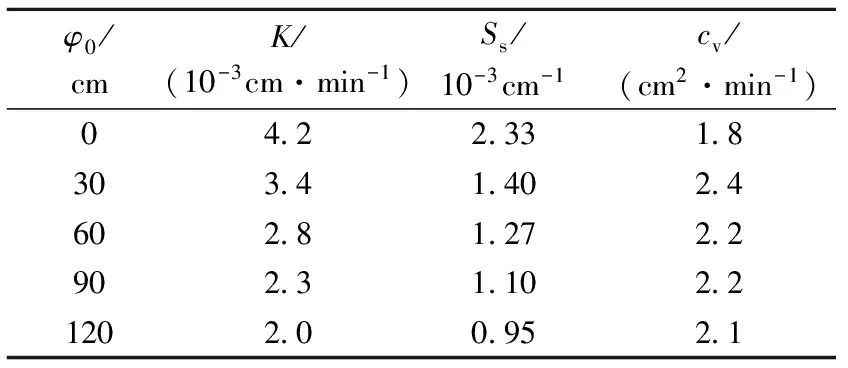
表2 土层参数计算结果

表1 配线法匹配点坐标

5次试验结束时土层的总变形量为3.1 cm,根据物质守恒定律(饱和土层的变形体积等于土层的释水量)可得试验结束时土层的总释水量为887 cm3。在Terzaghi一维固结理论中,假设土体固结变形过程中渗透系数和压缩系数保持不变,若取试验土层的渗透系数和贮水率值等于土体压缩变形初始阶段的值,弱透水层单位面积的释水量可通过下式计算得到:Vw=lφSsA/2=1 499 cm3[2-3]。该计算结果偏大69%,高估了弱透水层的释水量。同理,若取弱透水层的渗透系数和贮水率值等于土体压缩变形结束阶段的值,计算得Vw=611 cm3。该结果偏小31%,低估了弱透水层释水量,因此假设弱透水层释水固结过程中其水文地质参数不变是不合理的。利用上述5次试验得到的贮水率值,计算5次试验中土层释水量分别为300 cm3、174 cm3、154 cm3、131 cm3、111 cm3,总释水量为870 cm3。计算结果与实际释水量很接近,误差为1.9%(主要由测量误差和土层的饱和度引起),验证了配线法计算弱透水层贮水率的精度。

弱透水层释水滞后于相邻含水层的降深,相邻含水层定降深条件下弱透水层释水现象的滞后时间为[12]

(9)

τ0取决于弱透水层的水力参数和厚度,将5次试验的土层参数代入式(9)可得τ0分别为500 min、348 min、364 min、351 min、355 min。第一次试验中,土层初始孔隙比较大,变形量较大造成滞后释水完成所需时间较长;后面连续4次试验土层的释水现象完成时间约为355 min,即水流达到稳定所需要的时间基本相同。

3 结 语

基于相邻含水层降深恒定且初始时刻水流稳定条件下弱透水层释水量的解析解,提出参数求解的配线法,利用自发研制的试验装置,通过室内试验对弱透水层释水过程中水力参数的响应规律进行研究。结果表明:弱透水层的释水滞后于相邻含水层的降深变化,释水速度由大变小,至释水现象结束变为零;随着弱透水层的释水固结,弱透水层的渗透系数和贮水率随孔隙比的减小而逐渐减小,固结系数有减小趋势,但变化不大,试验土层孔隙比减小0.19(不足20%),渗透系数和贮水率分别减小了52%和59%;假设弱透水层水力参数不变会对其释水量的计算造成较大误差,试验土层的渗透系数和贮水率分别取土层变形初始阶段和结束阶段的贮水率,弱透水层释水量计算结果分别偏大69%和偏小31%;弱透水层滞后释水现象的滞后因子在释水固结过程中基本不变,即释水现象完成的时间基本相同。

研究成果对地面沉降预测和地下水资源量计算具有一定的应用价值。本文对弱透水层释水固结过程中水力参数的变化规律进行探讨,未考虑弱透水层变形量较大时对水文地质参数反演的影响,需作进一步的研究。

[ 1 ] 周志芳,郑虎,庄超.论地下水资源的永久性消耗量[J].水利学报,2014,45(12): 1458-1463.(ZHOU Zhifang,ZHENG Hu,ZHUANG Chao.Study on the unrecoverable depletion of groundwater resource [J].Journal of Hydraulic Engeering,2014,45(12): 1458-1463.(in Chinese))

[ 2 ] KONIKOW L F,NEUZIL C E.A method to estimate groundwater depletion from confining layers[J].Water Resources Research,2007,43(7): 931-936.

[ 3 ] LI Zhaofeng,ZHOU Zhifang,CHEN Zhou,et al.An analytical method to estimate groundwater depletion from a confining layer[J].Natural Hazards,2017,85(2): 887-901.

[ 4 ] XUE Yuqun,ZHANG Yun,YE Shujun,et al.Land subsidence in China[J].Environmental Geology,2005,48(6): 713-720.

[ 5 ] NEUZIL C E.Groundwater flow in low-permeability environments[J].Water Resources Research,1986,22(8): 1163-1195.

[ 6 ] YAN Xiuping,KERRICH R,Hendry M J.Distribution of the rare earth elements in porewaters from a clay-rich aquitard sequence,Saskatchewan,Canada[J].Chemical Geology,2001,176(1/2/3/4): 151-172.

[ 7 ] 李平,金奕潼,赖建英,等.负压条件下土体渗流固结特性研究综述[J].河海大学学报(自然科学版),2016,44(2): 115-121.(LI Ping,JIN Yitong,LAI Jianying,et al.Review of research on characteristics of seepage-induced consolidation of soil under negative-pressure reinforcement conditions [J].Journal of Hohai University (Natural Sciences),2016,44(2): 115-121.(in Chinese))

[ 8 ] LI Zhaofeng,ZHOU Zhifang.An analytical solution for leakage rate and depletion of aquitard influenced by the delayed yield phenomenon[J].Environmental Earth Sciences,2015,74(2): 1227-1234.

[ 9 ] ZHUANG Cao,ZHOU Zhifang,ZHAN Hongbin,et al.A new type curve method for estimating aquitard hydraulic parameters in a multi-layered aquifer system[J].Journal of Hydrology,2015,527: 212-220.

[10] NEUZIL C E.How permeable are clays and shales?[J].Water Resources Research,1994,30(2): 145-150.

[11] 李绪谦,谢雪,李红艳,等.pH值对弱透水层中硝酸盐迁移转化的影响[J].水资源保护,2011,27(1): 67-72.(LI Xuqian,XIE Xue,LI Hongyan,et al.pH impact on nitrate migration and transformation in the aquitard [J].Water Resources Protection,2011,27(1): 67-72.(in Chinese))

[12] SHI Xiaoqing,XUE Yuqun,YE Shujun,et al.Characterization of land subsidence induced by groundwater withdrawals in Su-Xi-Chang Area,China[J].Environmental Geology,2007,52(1): 27-40.

[13] WU Jichun,SHI Xiaoqing,XUE Yuqun,et al.The development and control of the land subsidence in the Yangtze Delta,China[J].Environmental Geology,2008,55(8): 1725-1735.

[14] FIELD E H.A comparison and test of various site-response estimation techniques including three that are not reference-site dependent[J].Bulletin of the Seismological Society of America,1995,85(4): 1127-1143.

[15] LERMO J,CHAVEZGARCIA F J.Are microtremors useful in site response evaluation?[J].Bulletin of the Seismological Society of America,1994,84(5): 1350-1364.

[16] FIELD E,JACOB K.The theoretical response of sedimentary layers to ambient seismic noise[J].Geophysical Research Letters,1993,20(24): 2925-2928.

[17] 余闯,刘松玉.考虑应力水平的软土固结系数计算与试验研究[J].岩土力学,2004,25(增刊2): 103-107.(YU Chuang,LIU Songyu.Calculation and experiment on consolidation coefficient for soft clay considering different stress levels [J].Rock and Soil Mechanics,2004,25(Sup2): 103-107.(in Chinese))

[18] 张明,赵月平,王威,等.考虑有效应力的软土固结系数变化规律[J].北京工业大学学报,2010,36(2): 199-205.(ZHANG Ming,ZHAO Yueping,WANG Wei,et al.Variation characteristics of coefficient of consolidation for soft soil considering effective stress [J].Journal of Beijing University of Technology,2010,36 (2): 199-205.(in Chinese))

[19] 叶淑君,薛禹群.应用沉降和水位数据计算上海地区弱透水层的参数[J].岩土力学,2005,26(2): 256-260.(YE Shujun,XUE Yuqun.Stress-strain analysis for storage coefficients and vertical hydraulic conductivities of aquitards in Shanghai area [J].Rock and Soil Mechanics,2005,(02): 256-260.(in Chinese))

[20] ZHOU Zhifang,GUO Qiaona,DOU Zhi.Delayed drainage of aquitard in response to sudden change in groundwater level in adjacent confined aquifer: analytical and experimental studies[J].Chinese Science Bulletin,2013,58(25): 3060-3069.

[21] TERZAGHI K.Theoretical soil mechanics[M].New York:John Wiley and Sons,Inc,1943.

[22] ZHOU Zhfiang,WANG Jinguo,HUANG Yong,et al.Conceptual data model and method of settlement calculation for deformation and water release from saturated soft soil[J].Environmental Earth Sciences,2014,71(9): 4235-4245.

Variation of hydraulic parameters of aquitard during water release

LI Zhaofeng1,2,3, ZHOU Zhifang3, LI Mingyuan3, ZHOU Cuiying1,2

(1.SchoolofEngineering,SunYat-senUniversity,Guangzhou510275,China; 2.ResearchCenterforGeotechnicalEngineeringandInformationTechnology,SunYat-senUniversity,Guangzhou510275,China; 3.SchoolofEarthScienceandEngineering,HohaiUniversity,Nanjing211100,China)

In order to improve the accuracy of groundwater transport simulation, groundwater resources assessment, and land subsidence prediction, the variation of hydraulic parameters of an aquitard during water release was analyzed through laboratory testing. Based on the analytical solution of the water release quantity of an aquitard under the condition that the drawdown of the adjacent aquifer is constant and the flow in the aquitard is stable at the initial time, a type curve method for calculation of parameters is proposed, and experimental research was carried out using the self-developed test equipment. The experimental results show that the hydraulic conductivity and specific storativity decrease gradually with the water release from the aquitard, but the consolidation coefficient changes little. The hydraulic conductivity and specific storativity of the soil layer in the experiment were decreased by 52% and 59%, respectively. The assumption that hydraulic parameters are constant will lead to a significant error in the calculation of the water release quantity of the aquitard. The calculated water release quantity of the aquitard is larger than the actual value when the specific storativity in the initial stage of consolidation is used, but the opposite conclusion is obtained when the specific storativity in the final stage of consolidation is used.

aquitard; analytical solution; water release quantity; hydraulic parameter; delay index

10.3876/j.issn.1000-1980.2017.04.009

2016-06-12

国家自然科学基金(41572209);国家重点研发计划(2016YFC0402803)

李兆峰(1987—),男,山东安丘人,助理研究员,博士,主要从事地质资源与地质工程研究。E-mail: Lizhfzx@gmail.com

P641

A

1000-1980(2017)04-0340-05