基于元胞自动机模型的内陆河三角洲堆积体演化过程

2017-07-18李晓坤李勇涛

河海大学学报（自然科学版） 2017年4期

李晓坤,陈珺,黄华,李勇涛

(1.河海大学水文水资源与水利工程科学国家重点实验室,江苏南京 210098; 2.河海大学水利水电学院,江苏南京 210098; 3.中石油煤层气有限责任公司忻州分公司,山西忻州 036600; 4.太湖流域管理局水利发展研究中心,江苏苏州 215000)

李晓坤1，2,陈珺1，2,黄华3,李勇涛4

通过建立二维元胞自动机模型,对山区河流直接进入开阔湖区后的内陆河三角洲堆积体演化过程进行研究。分析三角洲堆积体的发展过程和堆积体表面冲积河槽形态演变的规律。总结得出整体规律:先纵向推进,再垂向淤积抬升,最后横向展宽;纵向推进速率随着模拟步数的增加而减小;垂向逐渐淤积抬升;横向展宽速率随着模拟步数的增加而逐渐减小;堆积体表面的河槽形态演化分为顺直、分汊和微弯河槽3个阶段。模拟结果与已有类似物理模型试验结果基本吻合,表明元胞自动机模型可以用于模拟三角洲演化的过程。

元胞自动机;内陆河三角洲堆积体;河道演化;冲积河槽

山区河流比降大、流速快,水流的挟沙能力强,进入开阔湖区后,横向受阻约束消失,流速减小使水流所携带的大量泥沙在山区河流出口处沉降淤积,形成三角洲堆积体[1-3]。三角洲堆积体的形成过程对外界环境具有很强的开放性,使得相关的动力学过程具有异常的复杂性。除此以外,三角洲要经过数十年甚至更久才能达到相对稳定状态,堆积体表面才能形成稳定的河道形态,有巨大时间尺度的累积效应。这些都给模型研究带来很大的困难。

元胞自动机模型作为一种时空离散的局部动力学模型,是研究复杂系统随机性和自组织性的主要方法之一[4-7]。Murra等[8]首先将元胞自动机模型应用于辫状河流的模拟。Coulthard等[9]采用了一种新的扫描算法元胞模型模拟了较大时空尺度上的山区河流冲积扇的演变。Seybold等[10]通过元胞自动机模型来模拟不同类型三角洲的形成。也有很多学者试图通过物理模型试验揭示冲积河流水流泥沙造床的规律。Lucy等[11]在3m×3m的河床上对冲积扇的演变过程及表面河槽变化进行了试验研究。刘飞等[12]重点对水沙从山区进入浅窄水域过程中三角洲堆积体的形成规律进行试验研究。国内外的学者从物理模型试验和水沙数学模型研究三角洲堆积体的形成过程,但是还未能通过元胞自动机模型对内陆河三角洲堆积的形成规律作系统阐述。笔者针对前人已有的试验结论,忽略实际河道的复杂形态,将元胞自动机应用到研究山区河流直接进入开阔湖区后三角洲堆积体的形成过程和堆积体表面河槽形态演替规律的模拟中,为研究内陆河三角洲堆积体的形成过程作进一步探索。

1 元胞自动机模型

元胞自动机模型由4个部分组成,分别是:元胞、元胞空间、邻居和转换规则。元胞是元胞自动机最基本的组成部分。元胞所分布的空间网点集合就是元胞空间。在一维元胞自动机中,通常以半径来确定邻居。转换规则,即根据元胞当前状态及其邻居状况确定下一时刻该元胞状态的动力学函数,即状态转移函数。散布在规则格网中的每一个元胞取有限的离散状态,遵循同样的作用规则,依据确定的局部规则作同步更新。大量元胞通过简单的相互作用构成动态系统的演化[13]。

1.1 元胞空间、状态及邻域类型

使用元胞模型首先要确定元胞空间,将山区河流概化成等宽的河道,宽度为20个元胞,长度为200个元胞,河道的坡度为0.1%。开阔水体的宽度为80个元胞,长度为100个元胞。在河道两侧设置高墙阻水,在模拟过程中模型边界没有挟沙水流的出入。图1给出了概化初始地形的高程(其中Z为高程)。本文采用摩尔(Moore)型邻域类型,建立中心元胞与下游3个方向邻近元胞的水沙输移规则。若中心元胞高程较下游元胞高则规定坡度为正坡,反之为负坡。

图1 概化初始地形高程Fig.1 Generalization of initial topography

1.2 水沙输移规则

流量分配常采用多流路算法,本文采用Murra等[14]提出的元胞模型水沙输移规则。

1.2.1 流量输移规则

建立流量输移与坡度的关系,规定当中心元胞到下游3个元胞方向的坡度至少有一个为正时,流量输移规则如下:

(1)

式中:Qi——第i个元胞的入流流量;n——常数,依据曼宁公式n取0.5;Si——中心元胞到第i个元胞的坡度;Sj——中心元胞到第j个元胞的坡度;Qo——中心元胞出流流量。

当坡度均为0时,流出中心元胞水流均匀分配给下游3个元胞。当坡度均为负时,考虑水流爬坡,流量按如下规则分配:

(2)

1.2.2 泥沙输移规则

纵向泥沙输移方向与流量输移规则相同,均由中心元胞向下游3个方向邻近元胞输移:

(3)

式中:Qsi——中心元胞向下游第i个元胞的输沙量;K,m——常数,K=10-21,m=2.5;Cs——常数,表示相邻行元胞之间高程差的平均值,具体可根据实际情况进行调整。

河流在自然演变过程中,不仅有纵向上的河床冲淤变化,横向受到二次流作用还存在显著的摆动特征。根据Parker[15]提出的横向输沙率表达式简化后得到横向泥沙输移法则:

(4)

式中:Qsl——横向输沙量;Kl——横向输移系数,取10-7;Sl——元胞横向坡度;Qso——中心元胞泥沙输出量。

2 模拟过程及结果分析

2.1 整体规律

模型模拟初期,堆积体呈现先沿着水流方向纵向发展推进,再垂向淤积抬升,最后横向展宽的规律(图2,T表示模拟步数)。

图2 不同模拟步数堆积体形态变化Fig.2 Changes in accumulation morphology with different simulation steps

进入开阔区域的水流因为惯性作用不会立即停止,经过与周围水体的混掺,流速减小,水体中的泥沙沿着流程开始落淤,并且随着水流作用向前推移加长,形成明显的舌状堆积体。随着模拟步数的增加,舌状堆积体前缘部分逐渐淤积抬升,阻挡水流泥沙的纵向输移,河槽主流向两侧摆动使其表面产生很多细小的分流口。分流口增多使堆积体表面的横向输沙能力得以增强,堆积体两侧淤积抬升,又形成居中的顺直河道。水流泥沙沿着居中河槽,堆积体前缘会淤积抬升,使堆积体表面的河槽慢慢地萎缩减小,上游水深增大,水流向堆积体两侧漫溢,形成一个树枝状的堆积体,见图2(a)。

随着模拟步数的增大,在逐渐成形的堆积体表面会形成顺直河槽、分汊河槽和微弯河槽。水流泥沙沿着河槽纵向推进,堆积体前缘部分发生淤积抬升,使上游水深增加,引起上游河槽分流现象。漫流初期的细小分流口垂直于边壁展宽,当两侧淤积抬升到一定高度时会限制细小分流口的发展,进而挟沙水流沿着堆积体两侧向下游输移,加快向下游的纵向推进速度。细小河槽挟沙能力增加,使河槽产生侧蚀现象,此时横向输沙不再垂直于边壁,而是与边壁的方向斜交,使河槽慢慢地向堆积体中间发展,形成微弯河槽。当堆积体前缘部分再次抬到一定程度的时候又会引起上游水位上升,又在堆积体两侧形成细小分流口,重复以上规律。不同模拟步数下堆积体的形态变化如图2所示。

2.2 纵向推进规律

堆积体在纵向推进、垂向淤积抬升和横向展宽过程中,首先呈现出来的是堆积体前缘的变化,前缘部分的形成规律能反映整个堆积体的发展过程。通过分析不同模拟步数下的河道形态图和堆积体平面图,可以得出:T=0～50 000步内,堆积体表面以顺直河槽和分汊河槽为主;T=50 000～100 000步内,堆积体表面以微弯河槽为主。

用最大流量的元胞连线表示堆积体表面的河槽形态,因为对每一个元胞来说,体积相同,流量最大则流速最大,本质上可以是动力轴线的体现。不同模拟步数河槽形态变化结果见图3。

图3 不同模拟步数河槽形态变化Fig.3 Changes in channel morphology with different simulation steps

当堆积体表面的河槽形态主要是顺直河槽时,堆积体前缘以居中摆动方式推进为主。在模拟初期,堆积体表面以顺直居中河槽和两侧有很多细小分流口为主,见图3(a)。随着模拟步数的增加,堆积体左右两侧淤积抬升,水流归主槽,在堆积体表面出现顺直河槽。随着顺直河槽堆积体前缘淤积抬升,上游河槽的水位上升,引起上游河槽出现分流现象,最后出现分汊河槽。从图3(c)可以看出,2条分汊河槽两侧的滩地及分汊之间的堆积体都会对分汊河槽起到约束作用,使挟沙水流向着两汊方向输移,当外侧堆积体的高度足够高时,会阻碍挟沙水流向边壁输移,折返向堆积体中间方向推进。所以当堆积体表面以分汊河槽为主时,堆积体前缘的纵向推进方式是:分汊河槽到堆积体两侧再到堆积体中间。

堆积体表面以微弯河槽为主时,前缘体的纵向推进方式为沿着堆积体中间向堆积体两侧摆动和沿两侧向河床中间摆动。如图3(c)中,微弯河槽是呈现中间偏左的,水流泥沙沿着从箭头1到箭头2的方向进行横向输移,在泥沙不断淤积抬升中从堆积体左侧向堆积体中间进行横向输移。在向中间偏移的时候,第200列元胞处的2个分汊,左汊发育更加充分,弯曲系数更大,导致右汊变小。随着模拟步数的增加,堆积体前缘的横向摆动减小,纵向推进基本停止,上游水深增加使上游的分汊河道发展更加充分,见图3(d)。堆积体前缘随不同模拟步数所在断面情况如下:模拟步数T为10 000步、25 000步、40 000步、50 000步、60 000步、75 000步、85 000步、100 000步时,相应的堆积体前缘所在断面分别是第242列元胞、第253列元胞、第265列元胞、第283列元胞、第289列元胞、第293列元胞、第295列元胞。模拟初期水流泥沙刚进入宽阔区域,纵向推进速率v较大,随着模拟步数的增加,v减小,如图4(a)所示(v=元胞数量/T)。根据不同模拟步数下堆积体形态的变化,可以发现堆积体在T=50 000步之前的纵向推进面积A变化较快,T=50 000步之后A变化较慢(如图4(b)所示)。图5为物理模型试验不同历时下纵向推进速率v′和纵向推进面积A′变化[12]。对比图4和图5，可以看出两者的变化形态类似。

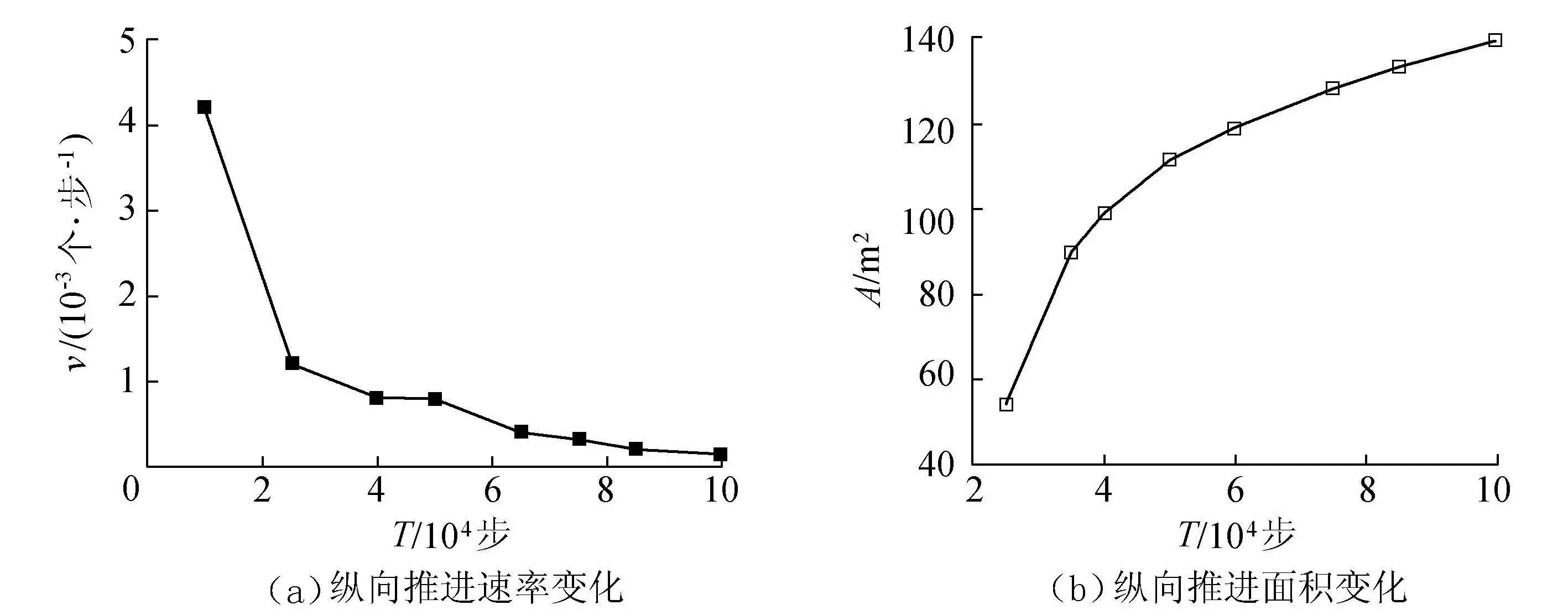
图4 不同模拟步数下纵向推进面积和纵向推进速率变化Fig.4 Changes in longitudinal forward area and rate with different simulation steps

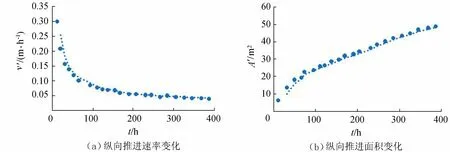
图5 物理模型试验不同历时下纵向推进面积和纵向推进速率变化Fig.5 Changes in longitudinal forward area and rate under different durations in physical model test

2.3 垂向抬升规律

堆积体的断面形态可以反映堆积体的垂向抬升规律和堆积体表面的河槽摆动变化过程。选取第250、260、270和280列元胞作为典型断面,研究分析其淤积抬升的规律。由图6可以发现在第250列元胞中间区域的居中河槽和左、右侧区域的滩地都同步淤积抬升。第260列元胞的断面形态说明在T=50 000步和T=75 000步时,发生了中间偏右的微弯河槽,右侧堆积体被冲刷,左侧发生淤积,水流泥沙沿着河槽向前推进的过程中逐级抬升。第270列元胞,河槽变得宽浅,流速减小,水流的挟沙力减小。可以从断面形态看出堆积体表面的河槽逐渐往右侧偏移,使整个断面往左右均匀淤积的方向发展。第280列元胞,断面表现出左右两侧堆积体交替冲淤的现象,在堆积体表面形成明显的居中河槽,堆积体左右两侧的淤积不均匀,左侧的淤积更快一些,与堆积体前缘变化规律一致。

图6 堆积体不同模拟步数断面形态Fig.6 Cross-sectional morphology of accumulation with different simulation steps

2.4 横向展宽规律

堆积体横向展宽先快后慢,根据前缘体纵向推进规律,随着模拟步数的增加,在堆积体表面形成不同的河槽进行纵向和横向的输移过程,堆积体在模拟初期先成舌状的形态,然后演变成树枝状的堆积体。到T=50 000步时,堆积体左右两侧形成很多细小的分流口,先沿着垂直边壁的方向输移,后在侧向侵蚀作用下斜向边壁方向输移。不同断面随着模拟步数的增加,横向展宽B如图7所示。

3 结语

图7 不同模拟步数下横向展开宽度变化Fig.7 Change in lateral spreading width with different simulation steps

a. 内陆河三角洲堆积体形成过程遵循3个规律,即纵向推进规律、垂向变化规律和横向展宽规律。(a)纵向推进规律:堆积体在山区河道出口处先在纵向上发展较快,形成舌状堆积体,三角堆积体表面光滑。随着模拟步数增加前缘逐渐抬升,进而阻碍水流泥沙的前进,挟沙水流在堆积体前以漫流的形式展开,在堆积体两侧形成很多细小的串沟,纵向推进速率减缓。(b)垂向变化规律:滩槽在垂向上整体处于淤积抬升状态,抬升速率逐渐减小。(c)横向展宽规律:水流泥沙在三角洲堆积体表面河槽的摆动中进行横向输移,扩展速率随着模拟步数的增加而减缓。

b. 在恒定来水来沙作用下,堆积体表面冲积河槽的形态变化分为3个阶段,依次为顺直河槽、分汊河槽和微弯河槽阶段。

以上结果与类似物理试验存在相似的结论,表明元胞自动机模型可以用于模拟山区河流直接进入开阔湖区形成三角洲堆积体的过程。三角洲的形成过程具有巨大的时间和空间的累积效应,元胞自动机模型作为一种时空离散的局部动力学模型,可以模拟较大尺度的时间、空间演化过程。本文只是初步对概化的山区河道和开阔湖区进行模拟,以揭示实际内陆河三角洲堆积体演化的一些定性规律。如何实现对其进行定量精确模拟,需要进一步完善和改进元胞自动机模型。

[ 1 ] 钱宁,张仁,周志德.河床演变学[M].北京:科学出版社,1987.

[ 2 ] 谢鉴衡.江河演变与治理研究[M]. 武汉：武汉大学出版社,2004.

[ 3 ] YANG Fan, JIA Jinghua. Alluvial fan and fandelta sedimentary facies and favorable assemblage of reservoir and seal of Wushi Sag(Cretaceous) in TarimBasin [J]. Acta Sedimentologica Sinica,2006,24(5):681-689.

[ 4 ] 黄翀,刘高焕.元胞模型在地貌演化模拟中的应用浅析[J].地理科学进展,2005,24(1):105-115.(HUANG Chong, LIU Gaohuan. A review of application of celluarmodels in landscape evolution modeling[J]. Progress in Geography,2005,24(1):105-115.(in Chinese))

[ 5 ] NEUMANN V. Theory of self-reproducing automata [M]. Urbana: University of Illionois,1966.

[ 6 ] 张俊勇,陈立,吴华林,等.水系形成与发展的元胞自动机模型研究[J].水科学进展,2007,18(5):695-700.(ZHANG Junyong, CHEN Li,WU Hualin,et al. Cellular model for the form and development of drainage system[J].Advances in Water Science,2007,18(5):695-700.(in Chinese))

[ 7 ] THOMAS R,NICHOLAS T P. Simulation of braided river flow using a new cellular routing scheme[J].Geomorphology,2002,43:179-195.

[ 8 ] MURRA Y, PAOLA C.A cellular model of braided rivers[J].Nature,1994,371:54-57.

[ 9 ] COULTHARD T J, MACKLIN M G, KIRBY M J. A cellular model of Holocene Upland River Basin and Alluvial Fan Evolution[J]. Earth Surface Processes and Landforms,2002,27:269-288.

[10] SEYBOLD H, RADE J, HERRMANN H. Modeling river geophsics[J]. PANS,2007,104(43):16804-16809.

[11] LUCY C, TIMOTHY A.An experimental investigation of autogenic behavior during alluvial fan evolution[J].Geomorphology, 2010,115:278-285.

[12] 刘飞,张小峰,任实. 窄浅水域三角洲堆积体形成规律的试验研究[J].水力发电学报,2014,33(2):137-145.(LIU Fei, ZHANG Xiaofeng, REN Shi. Experimental study on formation pattern of delta deposition in the shallow and narrow water basins[J]. Journal of Hydroelectric Engineering, 2014,33(2):137-145.(in Chinese))

[13] 张敏,吴花芹,赖瑞勋,等.元胞自动机在河道演变模拟中的应用[J].人民黄河,2011,33(11):7-9.(ZHANG Min, WU Huaqin, LAI Ruixun, et al. Review of Application of cellular models to the river evolution[J]. Yellow River, 2011,33(11):7-9.(in Chinese))

[14] MURRA Y, PAOLA C. Properties of a cellular braided-stream model[J]. Earth Surface Processes and Landforms,1997, 22:1001-1025.

[15] PARKER G. On the cause and characteristic scales of meandering and braiding in rivers[J]. Journal of Fluid Mechanics,1976,111: 457-480.

Evolution process of delta accumulation in inland river based on cellular automata model

LI Xiaokun1，2, CHEN Jun1,2, HUANG Hua3, LI Yongtao4

(1.StateKeyLaboratoryofHydrology-WaterResourcesandHydraulicEngineering,HohaiUniversity,Nanjing210098,China; 2.CollegeofWaterConservancyandHydraulicEngineering,HohaiUniversity,Nanjing210098,China; 3.XinzhouBranchCompany,PetrochinaCoalbedMethaneCompanyLimited,Xinzhou036600,China; 4.WaterResourcesDevelopmentResearchCenterofTaihuBasinAuthority,Suzhou215000,China)

Through establishment of a two-dimensional cellular automata model, the evolution process of delta accumulation in inland rivers after a mountain river flows directly into open lake areas was examined. The development process of delta accumulation and the evolution laws of alluvial channel morphology on the accumulation surface were analyzed. The whole pattern was determined: first longitudinal forward, then vertical deposition uplift, and finally lateral spreading. The longitudinal forward rate decreases with the increase of the simulation steps, a gradual deposition uplift occurs in the vertical direction, and the rate of lateral spreading decreases with the increase of the simulation steps. The channel morphology evolution on the accumulation surface can be divided into three stages: the straight channel, braided channel, and micro-bend channel. The simulated results agree with existing experimental results of the physical model, indicating that the cellular automata model can be used to simulate the evolution process of the delta.

cellular automata; delta accumulation in inland river; river evolution; alluvial channel

10.3876/j.issn.1000-1980.2017.04.002

2016-08-08

国家自然科学基金(50909037)

李晓坤(1992—),男,江苏淮安人,硕士研究生,主要从事水力学及河流动力学研究。E-mail:151302010011@hhu.edu.cn

陈珺,副教授。E-mail: chenjunhhu@hhu.edu.cn

TV131.4

1000-1980(2017)04-0291-07