基于奇异向量频谱的工频干扰消除方法*

李伟光 张晓涛

(华南理工大学 机械与汽车工程学院， 广东 广州 510640)

基于奇异向量频谱的工频干扰消除方法*

李伟光 张晓涛†

(华南理工大学 机械与汽车工程学院， 广东 广州 510640)

针对旋转机械振动信号中的工频干扰问题，提出了基于奇异向量频谱的消除方法.振动信号经奇异值分解后，信号中的有用成分和工频分量被分解到不同的正交子空间.因奇异值谱表征信号中各个成分的能量分布，故先由奇异值谱估计与工频相应的奇异向量所在的子空间范围，然后在该范围的子空间内根据奇异向量的频谱特征确定与工频成分对应的奇异向量，进而确定工频成分对应的奇异值，将这些奇异值置0，用其余的奇异值和奇异向量重构为时域信号，从而达到消除工频干扰的目的.仿真和试验结果表明，所提出的工频干扰消除方法是有效的，在消除信号中工频干扰成分的同时不会影响信号的其他成分．

振动信号；工频干扰；奇异值分解;奇异向量

应用电涡流位移传感器测量转轴振动位移是振动测试领域的常规做法[1].如果采集的信号中存在电源干扰，则会影响对旋转机械的状态判断和故障诊断.因此，消除振动信号中的工频干扰是十分必要的．

目前消除50 Hz工频干扰的方法主要有两种滤波方法[2]:①陷波滤波法，即采用具有一定阻带宽度的陷波滤波器组来消除基频和谐波，如果信号频率和电网工频相混叠，则在滤除工频干扰的同时会造成有用信号的损失;②自适应滤波法，即采用自适应滤波算法实现工频成分的自适应抵消，该方法受自适应滤波器长度的影响很大．

奇异值分解(SVD)法在消除工频干扰方面有一定的应用，如张克南等[2]采用奇异值分解法消除电网工频干扰;吴浩浩等[3]通过往信号中添加50 Hz的正弦引导信号，使得50 Hz工频对应的奇异值为最大，从而消除工频干扰;翟亚宁等[4]通过奇异值分解法去除转子系统中的工频干扰等.以上研究将奇异值分解应用于工频干扰消除时，需要满足工频分量对应的奇异值在奇异值谱中为最大这个条件.但在工程实践中，信号中与转子振动特征有关的分量通常是主要的，而工频分量是次要的，故信号经奇异值分解后工频分量所对应的奇异值通常并不是最大的，因而上述应用奇异值分解来消除工频干扰的方法具有局限性．

旋转机械振动信号经奇异值分解后，得到奇异值和相应的奇异向量.以往对奇异值分解的研究都集中在奇异值[2- 6]，对奇异向量的研究则相对较少，但也有应用的例子，如梁霖等[7]对信号连续变换小波系数进行奇异值分解，在正交子空间中选择集成信号特征的奇异向量进行重构，以实现信号降噪;Groutage等[8]认为奇异向量包含信号的时频信息;杨恒等[9]提出了基于奇异值和奇异向量的多用户检测方法;徐晓华等[10]提出了基于奇异向量空间的基因表达双聚类算法;刘科峰等[11]采用奇异向量作为神经网络的输入，建立了云团运动的预测模型;刘文超等[12]将奇异向量和奇异值相结合应用于人脸识别等.但奇异向量在振动信号分析和工频干扰方面的应用则比较少见．

作为自适应信号分析方法，经验模式分解[13](EMD)在信号处理、故障诊断等领域得到了广泛的应用，但在信号工频成分消除方面的应用则较少．

文中将奇异值分解得到的奇异向量与其频谱特征相结合，通过频谱特征筛选奇异向量以确定对应于工频分量的奇异值在奇异值谱中的位置，从而克服文献[2- 4]在应用奇异值分解法消除工频干扰时存在的局限性；然后采用文中所提出的方法对仿真信号和试验数据进行分析，并与EMD方法和陷波滤波法进行了对比研究．

1 奇异向量频谱方法

对实数矩阵A∈Rm×n，存在正交矩阵U∈Rm×m和V∈Rm×n，使得下式成立:

A=UΛVT

(1)

式中，Λ为对角阵，Λ的秩为r，r≤min(m，n)，非零对角元素称为A的奇异值，按降序排列．

由于Λ为对角阵，故A经SVD分解后可表示为r个秩为1的m×n阶子矩阵和的形式，即

(2)

式中，Ui和Vi分别为矩阵A的第i个左奇异向量和右奇异向量,δi为矩阵A的第i个奇异值，Ai为子矩阵．

式(2)表明，矩阵A经过SVD后变成一系列的子矩阵Ai之和的形式，也就是将矩阵分解成相互正交的子空间，从而将矩阵包含的信息分解到不同的子矩阵中[14].包含工频成分的非平稳振动信号经SVD后，工频成分和其他信号分量被分解到不同的正交子空间，从而实现工频成分与信号中其他成分的分离．

由测得的离散数字信号x(i)(i=1,2,…,N)构造实矩阵A，有多种构造形式，Hankel矩阵是其中最常见的一种.当Hankel矩阵的行数为信号长度的一半时，信号分离效果最好[15]，故文中采用这种结构的Hankel矩阵.

基于奇异向量频谱的工频干扰消除方法的步骤如下:

(1)对信号进行奇异值分解，得到一系列奇异值和奇异向量;

(2)根据奇异值谱估计工频分量的左(右)奇异向量范围;

(3)对左(右)奇异向量作快速傅里叶变换(FFT)，根据频谱图确定对应于工频分量的奇异向量;

(4)依据奇异值和奇异向量的对应关系，将对应工频的奇异值置0，并重构为时域信号，从而得到无工频干扰的信号．

2 奇异向量分析

旋转机械发生故障时，振动信号具有非线性、非平稳的特征[16]，文中用工频和变频相结合的仿真信号进行模拟，并叠加强度为1的高斯白噪声ξ(t)，即

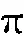
(3)

信号波形及频谱如图1所示,其中A为信号幅值.信号的信噪比为0.360 9，因信噪比较低，信号被噪声淹没．

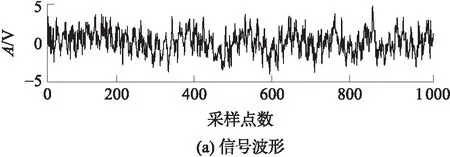
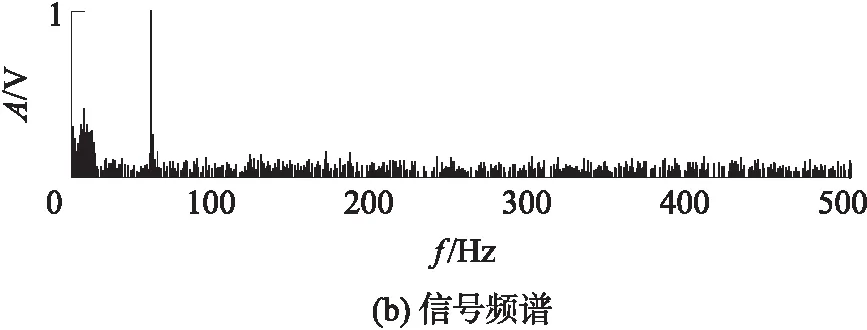
图1 仿真信号波形及频谱

对仿真信号进行奇异值分解，得到的奇异值谱如图2所示，生成的奇异值总数为512，但图中只显示前50个.由图2可见，较大的奇异值集中在前14个，其余奇异值接近0，因此，工频分量和变频分量对应的奇异值都集中在这范围内，但具体的对应关系并不清楚．

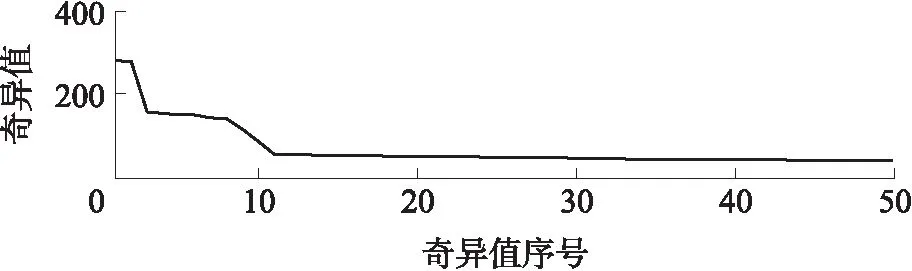
图2 仿真信号的奇异值谱

为深入理解奇异向量的性质，图3列出了前6个奇异向量波形，其他奇异向量波形类似.为便于比较，左、右奇异向量显示在同一幅图中，左奇异向量Ui为512个点，而右奇异向量Vi为513个点，采用左对齐的方式显示.图3表明，同一奇异值的左、右奇异向量或者完全重合(当i=1，4，6时)或者关于x=0轴对称(当i=2，3，5时).对左奇异向量U1、U2进行FFT，得到图4(a)所示的频谱，从图中可见两个奇异向量都是50Hz.对左奇异向量U3进行FFT，得到图4(b)所示的频谱，其他奇异向量的频谱与此类似.图4(b)的频谱与图4(a)的频谱完全不同，它位于更低的频段，从频谱结构可明显辨别出，左奇异向量Ui(i=1，2)对应工频分量，而U3对应变频分量.由于奇异向量和奇异值是对应的，因此在奇异谱中第1、第2个奇异值对应工频分量．

图3 仿真信号的奇异向量波形

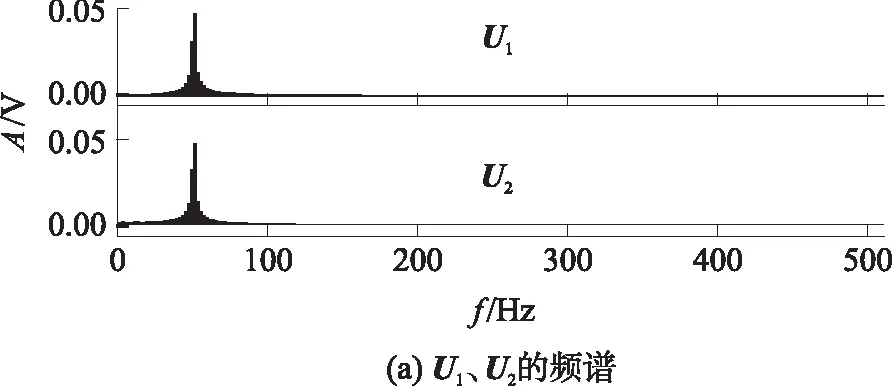
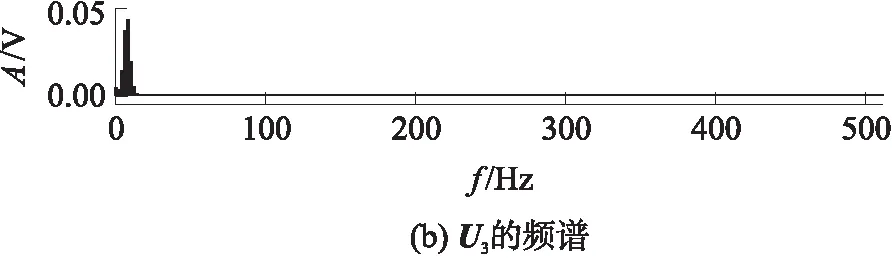
图4 左奇异向量U1、U2和U3的频谱

将第1、第2个奇异值置0，并重构为如图5所示的时域信号.为清晰显示工频成分的去除效果，将图1所示的原始信号与图5的重构信号做差分，得到图6的差分信号及其频谱.图6表明，工频成分得以完全去除，信号中其他成分基本上不受影响．

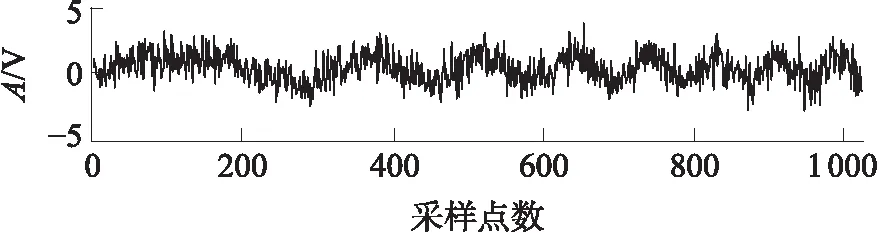
图5 去除工频后的变频信号

Fig.5 Variable-frequency signal after removing power frequency

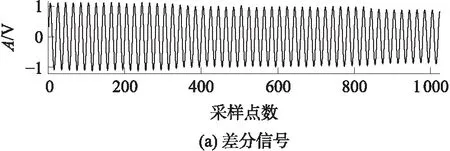
图6 差分信号及其频谱

作为对比，应用EMD方法对原始仿真信号f(t)进行处理，结果如图7所示，共生成8个内禀模式分量(IMF).由于噪声的影响，各IMF出现严重的模式混叠，并没有分离出如图6所示的工频成分，这表明EMD方法在消除工频干扰方面存在局限性．

图7 仿真信号的EMD处理结果

3 试验数据分析

为研究基于奇异向量频谱特征的工频干扰消除方法在工程上应用的可行性，将其用于消除可倾瓦轴承振动位移信号中的工频干扰．

传统的可倾瓦轴承(如图8所示)中各瓦块绕支点自由摆动以适应运转条件的变化，具有较好的稳定性，在汽轮机和风机等行业中获得了广泛的应用[17].但传统的可倾瓦轴承由于采用固定机械支点方式，使得轴承系统的运行稳定性下降，支点磨损而降低运行寿命.为此，文中研制了一种新的可倾瓦轴承(简称新型轴承)，采用内、外双层油膜结构，用油膜支承取代固定机械支点支承，从而起到良好的阻尼减振作用，同时避免机械磨损．

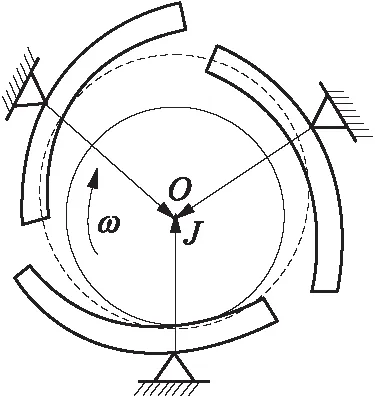
图8 传统的可倾瓦轴承示意图

为评估新型轴承的减振特性，搭建了大型轴承试验台，如图9所示.轴承试验台包括基座、大功率伺服电机、连接电机和前轴承的联轴器、前可倾瓦轴承、转子、后可倾瓦轴承、推力轴承、供油系统等.此外，试验台系统还包括电气控制柜及LMS数据采集系统等．

图9 新型轴承试验台

为实时监测转子的振动情况，在轴承试验台转子两侧的轴颈处，每侧以相互垂直的方式安装两个Kaman KD23061S电涡流位移传感器，每个传感器与垂直方向成45°的夹角，如图10所示．

图10 电涡流位移传感器安装示意图

在某次试验中，选用间隙比为0.25%的新型轴承，进油温度控制在工作范围内，进油压力调整为0.3 MPa，启动轴承润滑系统、伺服驱动电机系统及LMS数据采集系统.试验预备工作完成后，将转子转速由静止状态逐步提升到最高工作转速，在此过程中，以设置的采样率在某几个工作转速点连续采集数据并保存.

为验证基于奇异向量频谱特征的工频干扰消除方法的有效性，取转子转速为3 900 r/min，以采样率为1 024 Hz连续采集，截取信号长度为1 024的信号进行分析，信号波形和频谱如图11所示.由图可见，信号中存在50 Hz工频干扰.经研究发现，干扰来源于为KD2306S电涡流位移传感器供电的24 V直流稳压电源，直流稳压电源内部没有屏蔽掉工频干扰，导致电涡流传感器直流输出信号中混有电源工频成分．

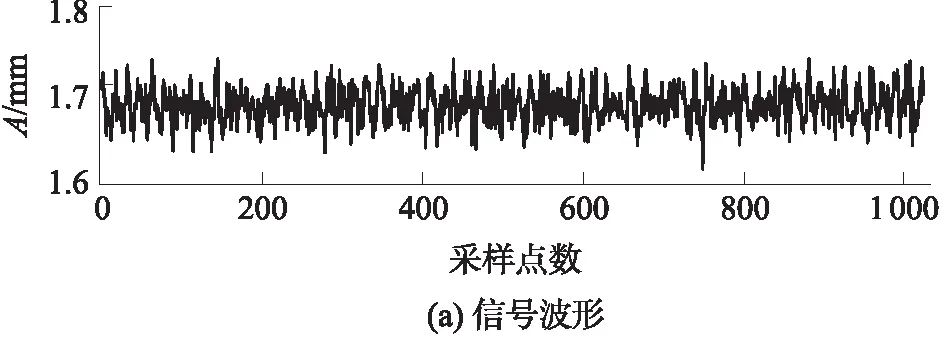
图11 振动位移信号波形及其频谱

由采集的振动位移信号构造Hankel矩阵，并进行奇异值分解，得到如图12所示的奇异值谱，图中只显示前50个奇异值，未包括直流分量对应的奇异值．

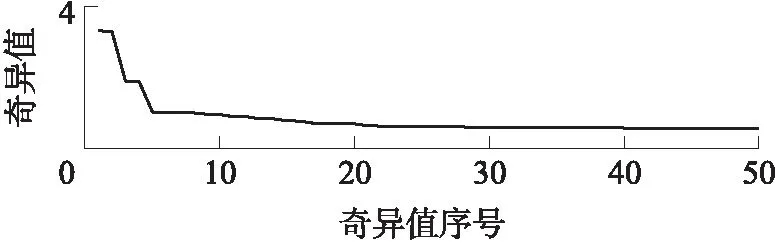
图12 试验信号的奇异值谱

根据奇异值分解理论，工频分量的频谱幅值只比转子基频稍小，因此工频分量对应的奇异值在奇异值分解后产生的奇异值谱中的位置也是靠前的，但并不知道具体位置.在图12的奇异值谱中，数值比较大的奇异值集中在前面5个，因此文中重点分析前6个奇异向量波形(含直流分量对应的奇异向量)，如图13所示.左奇异向量U1对应振动位移信号中的直流分量.对Ui(i=2，3，…，6)进行FFT，结果如图14所示，图中，U4和U5的频谱都为工频50 Hz，依据奇异值和奇异向量之间的对应关系，在奇异值谱中50 Hz对应第4和第5个奇异值，将这两个奇异值置0，重构为时域信号，重构的信号波形和频谱如图15所示.比较图15和图11发现，除了50 Hz工频成分被消除外，信号的其他成分不受影响.将图11所示信号与图15所示信号作差分，差分信号实际上就是被消除的工频干扰，结果如图16所示.差分信号完整清晰，说明振动信号中的50 Hz工频干扰被完全消除．

图13 试验信号的奇异向量波形

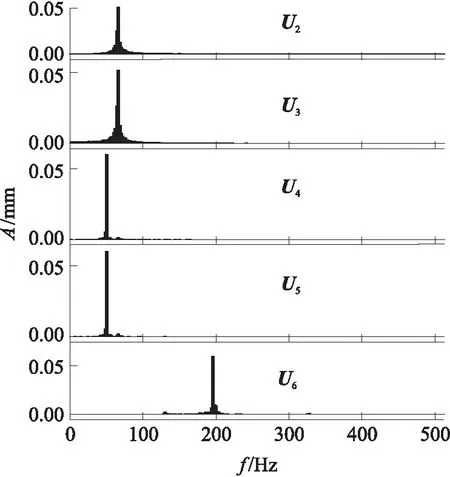
图14 试验信号的奇异向量频谱

图15 去除工频干扰的信号波形及频谱

Fig.15 Waveform and its spectrum of signal after removing power interference

图16 被消除的工频干扰信号

4 陷波滤波器和EMD的处理结果

针对试验信号，文中给出了常用陷波滤波器和EMD方法的处理结果，并与文中所提方法的结果进行对比分析．

根据无限冲击响应(IIR)数字滤波器理论[18]，50 Hz陷波器的传递函数为

(4)

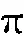
经陷波器滤波后的试验信号频谱如图17所示.比较图17和图15可以发现，经50 Hz陷波器滤波后，不但信号基频(65 Hz)幅值下降，而且其邻近的部分有用信号同时被过滤掉，从而会导致信号受损．

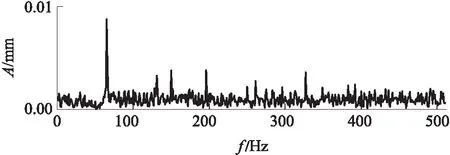
图17 陷波器滤波后的试验信号频谱

对试验信号作EMD，生成8个IMF，如图18所示.而这8个IMF没有分离出如图16所示的工频成分，这表明EMD方法用于消除工频干扰具有局限性．

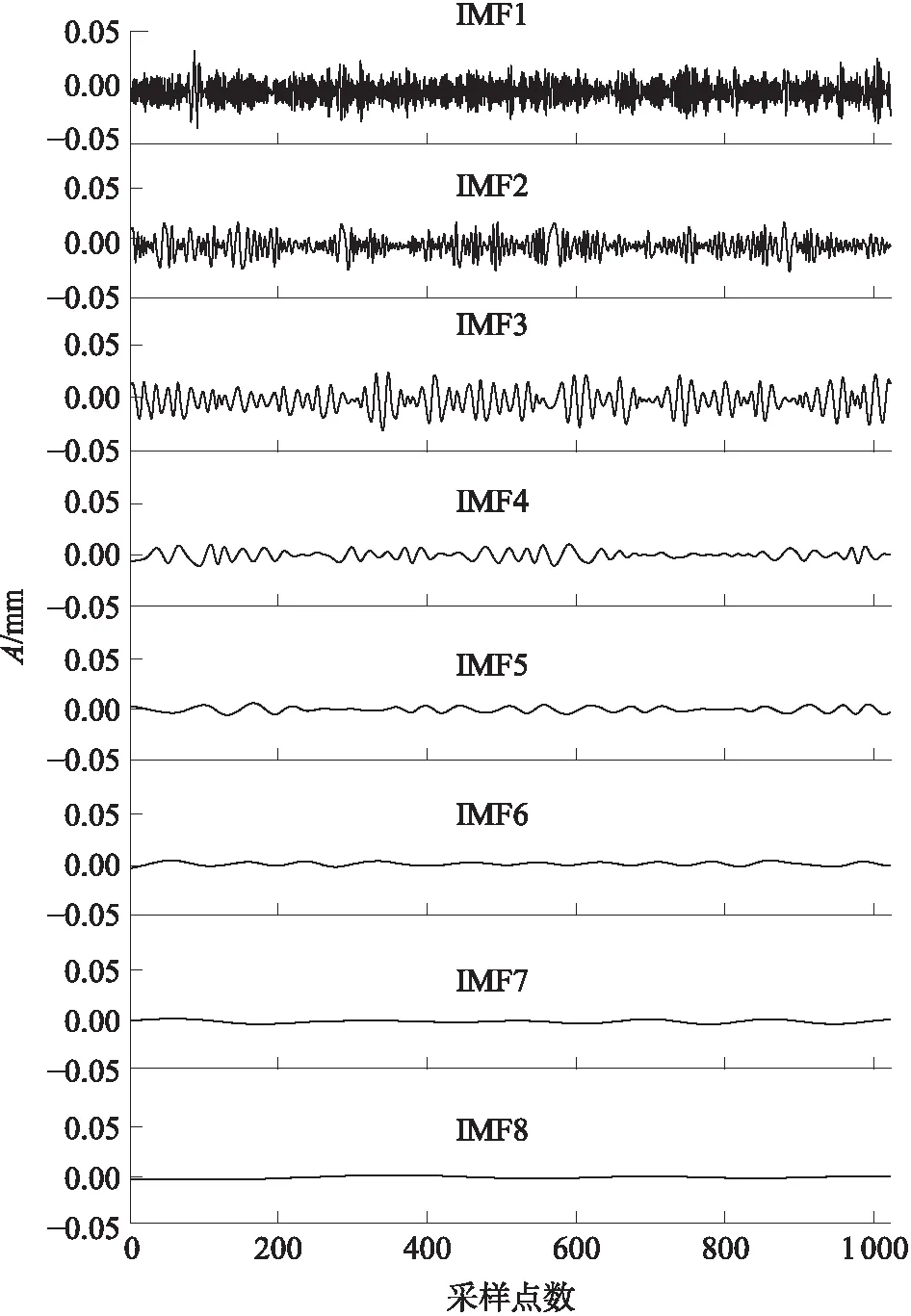
图18 试验信号的EMD处理结果

5 结论

文中提出了将奇异向量及其频谱特征相结合以消除振动位移信号中工频干扰的方法，并通过非平稳的仿真信号分析了左、右奇异向量的规律及其频谱特征，发现同一奇异值的左奇异向量和右奇异向量之间具有重合或关于x=0轴对称的关系，信号中各分量被分解到不同的奇异向量正交子空间，通过奇异向量频谱可以分辨对应的工频分量，从而得到对应的奇异值在奇异值谱中的位置，进而重构为无工频干扰的信号．

将文中所提出的方法应用于新型可倾瓦轴承电涡流振动位移信号的工频干扰消除，结果表明所提方法具有工程应用价值;与陷波滤波器和EMD方法对比结果表明，文中方法能够在不影响信号其他成分的情况下去除工频分量．

[1] 施维新，石静波.汽轮发电机组振动及事故 [M].北京:中国电力出版社，2008．

[2] 张克南，陆扬，谢里阳，等.基于SVD方法的弱故障特征提取方法 [J].机床与液压，2006(10):214- 216． ZHANG Ke-nan，LU Yang，XIE Li-yang，et al.A new method for extracting the weak fault symptoms of current signal via SVD [J].Machine Tool & Hydraulics，2006(10):214- 216．

[3] 吴浩浩，罗志增.基于构造Hankel矩阵的SVD陷波方法 [J].计算机应用研究，2010，27(12):4514- 4517． WU Hao-hao，LUO Zhi-zeng.Signal notch method based on Hankel matrix and SVD [J].Application Research of Computers，2010，27(12):4514- 4517．

[4] 翟亚宁，杨兆建.基于小波包能量谱和BP神经网络的转子系统扭矩激励识别 [J].中国农机化学报，2015，36(3):194- 198． ZHAI Ya-ning，YANG Zhao-jian.Torque incentive identification of the rotor system based on wavelet packet energy spectrum and BP neural network [J].Journal of Chinese Agricultural Mechanization，2015，36(3):194- 198．

[5] RUOCCI G，CUMUNEL G，LE T，et al.Damage assessment of pre-stressed structures:a SVD-based approach to deal with time-varying loading [J].Mechanical Systems and Signal Processing，2014，47:50- 65．

[6] GOLAFSHAN R，SANLITURK K Y.SVD and Hankel matrix based de-noising approach for ball bearing fault detection and its assessment using artificial faults [J].Mechanical Systems and Signal Processing，2016，70/71:36- 50．

[7] 梁霖，徐光华，侯成刚.基于奇异值分解的连续小波消噪方法 [J].西安交通大学学报，2004，38(9):904- 908．LIANG Lin，XU Guang-hua，HOU Cheng-gang.Continuous wavelet transformdenoisingmethodbased on singular value decomposition [J].Journal of Xi’an Jiaotong University，2004，38(9):904- 908．

[8] GROUTAGE D，BENNINK D.Feature sets for nonstatio-nary signals derived from moments of the singular value decomposition of Cohen-Posch(positive time-frequency) distributions [J].IEEE Transactions on Signal Proce-ssing，2000，48(5):1498- 1503．

[9] 杨恒，张贤达.基于奇异值和奇异向量的盲自适应多用户检测方法 [J].清华大学学报(自然科学版)，2001，41(3):101- 103． YANG Heng，ZHANG Xian-da.Singular value and singular vector based blind adaptive multiuser detector [J].Journal of Tsinghua University(Science & Technology)，2001，41(3):101- 103．

[10] 徐晓华，席艳秋，潘舟金，等.奇异向量空间双聚类算法 [J].微电子学与计算机，2012，29(3):78- 83． XU Xiao-hua，XI Yan-qiu，PAN Zhou-jin，et al.Singular vector space biclustering algorithm [J].Microelectronics and Computer，2012，29(3):78- 83．

[11] 刘科峰，张韧，李文才，等.奇异值分解与神经网络结合的卫星云图云团移动预测 [J].解放军理工大学学报(自然科学版)，2008，9(3):298- 301． LIU Ke-feng，ZHANG Ren，LI Wen-cai，et al.Cloud cluster movement forecast technique of satellite cloud pictures based on singular value decomposition and artificial neural networks [J].Journal of PLA University of Science and Technology，2008，9(3):298- 301．

[12] 刘文超，陈艳红.基于奇异向量和奇异值的人脸识别新方法 [J].桂林电子工业学院学报，2006，25(6):49- 52． LIU Wen-chao，CHEN Yan-hong.Face recognition approach based on singular vector and singular value [J].Journal of Guilin University of Electronic Technology，2006，25(6):49- 52．

[13] 马文朋，张俊红，马梁.改进的经验模式分解在机械故障诊断中的应用 [J].振动、测试与诊断，2015，35(4):637- 644． MA Wen-peng，ZHANG Jun-hong，MA Liang.Application of improved empirical mode decomposition in machinery fault diagnosis [J].Journal of Vibration，Mea-surement & Diagnosis，2015，35(4):637- 644．

[14] 赵玲，刘小峰，娄路.复小波分解联合SVD提取振动信号非平稳特征 [J].振动、测试与诊断，2015，35(4):672- 676． ZHAO Ling，LIU Xiao-feng，LOU Lu.The feature extraction method of non-stationary vibration signal based on SVD-complex analytical wavelet demodulation [J].Jour-nal of Vibration，Measurement & Diagnosis，2015，35(4):672- 676．

[15] 赵学智，叶邦彦，陈统坚.奇异值差分谱理论及其在车床主轴箱故障诊断中的应用 [J].机械工程学报，2010，46(1):100- 108． ZHAO Xue-zhi，YE Bang-yan，CHEN Tong-jian.Differen-ce spectrum theory of singular value and its application to the fault diagnosis of headstock of lathe [J].Journal of Mechanical Engineering，2010，46(1):100- 108．

[16] 何正嘉，訾艳阳，孟庆丰,等.机械设备非平稳信号的故障诊断原理及应用 [M].北京:高等教育出版社，2001．

[17] 张晓涛，李伟光.基于谐波小波和SVD的可倾瓦滑动轴承工频干扰抑制 [J].华南理工大学学报(自然科学版)，2016，44(10):1- 7． ZHANG Xiao-tao，LI Wei-guang.Power interference removal for tilting-pad journal bearing based on harmonic wavelet and SVD [J].Journal of South China University of Technology(Natural Science Edition)，2016，44(10):1- 7．

[18] 王立会，潘冬明.一种消除心电信号中工频干扰的陷波器设计 [J].医疗设备信息，2007，22(7):18- 20． WANG Li-hui，PAN Dong-ming.Design of digital trap for eliminating power-line interference on ECG signals [J].Information of Medical Equipment，2007，22(7):18- 20．

Removal Method of Power Interferences Based on Singular Vector Spectrum

LIWei-guangZHANGXiao-tao

(School of Mechanical and Automotive Engineering,South China University of Technology,Guangzhou 510640,Guangdong,China )

Proposed is a method on the basis of singular vector spectrum for the removal of power interferences in vibration signals of rotating machinery. In this method,firstly,vibration signals are processed through singular value decomposition,and the useful components as well as the power frequency components are divided into diffe-rent orthogonal subspaces. Then,as the singular vector spectrum reflects the energy distribution of each signal component,the subspace range of the singular vector corresponding to power interference is estimated according to the singular vector spectrum,in which singular vectors corresponding to power interferences are obtained by analyzing the spectrum features of singular vectors. Finally,the singular values corresponding to power interferences are determined and set to zero,and other singular values as well as singular vectors are used to reconstruct desired time-domain signals without power interferences. Simulated and experimental results demonstrate that the proposed method can effectively remove power interferences without any effect on other components of the vibration signal.

vibration signal；power interference；singular value decomposition;singular vector

2016- 09- 12

国家“863”计划项目(2015AA043005)；广州市南沙区科技计划项目(2014CX07) Foundation item: Supported by the National High- Tech R&D Program(863 Program) of China(2015AA043005)

李伟光(1958-),男,教授,博士生导师,主要从事机器人、旋转机械故障诊断研究.E-mail:wguangli@scut.edu.cn

†通信作者: 张晓涛(1973-),男,博士生,主要从事旋转机械故障诊断研究.E-mail:1792654107@qq.com

1000- 565X(2017)05- 0016- 08

TN 911.7;TH 113.1

10.3969/j.issn.1000-565X.2017.05.003