基于最小割图分割的社区发现算法

2017-07-18王亚珅黄河燕

中文信息学报 2017年3期

关键词：最大化节点模块

王亚珅，黄河燕，冯冲

(北京理工大学计算机学院北京市海量语言信息处理与云计算应用工程技术研究中心，北京 100081)

基于最小割图分割的社区发现算法

王亚珅，黄河燕，冯冲

(北京理工大学计算机学院北京市海量语言信息处理与云计算应用工程技术研究中心，北京 100081)

该文证明了模块度最大化问题可以被转换成为原网络上的最小割图分割问题，并且基于该证明提出了一种高效的社区发现算法。同时，该文创新性地将模块度理论与当今比较流行的统计推理模型相结合：首先，这些统计推理模型被转化为模块度最大化问题中的零模型；其次，统计推理模型中的目标函数被修改并应用于本文的最优化算法中。实验结果显示，无论是在真实世界网络还是在人工生成网络中，该文提出的算法均具有高效和稳定的发现社区的能力。

社区发现；模块度；最小割图分割

1 引言

作为网络的一种常见属性，社区结构(community structure)是一种对网络节点的分割，其中，同一个社区中的节点联系紧密，而隶属于不同社区的节点之间联系则相对松散[1-2]，社区发现(community detection)已经在诸多领域体现出其应用价值[3-5]。为了解决社区发现问题，我们首先讨论社区(community)的定义，学界目前存在很多全局化的社区定义，这些定义均将社区结构视为整个网络的一个属性[6]。

(1) 最为直观的社区定义与连接不同社区边的数量(在有权网络中，则为连接边的加权和)有关，这个数量通常被称为割规模(cut size)，旨在最小化割规模的问题一般被称为“最小割图分割(minimum-cut graph partitioning)”问题。

(2) 另一种社区的定义则是基于被广泛使用的模块度(modularity)概念[1,7]。模块度衡量一个给定的图分割与一个期望随机图(又称为“零模型”)的图分割之间的差异，旨在最大化模块度的问题一般被称为“模块度最大化(modularity maximization)”问题。

本文研究的核心内容是，探索模块度最大化问题和最小割图分割问题的内在关系。目前，学界对此类问题的相关研究较少。文献[8]针对生成一个特定网络的似然函数最大化问题，证明了统计推理模型可以映射成为最小割图分割问题。本文的研究正是受文献[8]启发，但是我们重点关注的是模块度最大化问题，证明模块度最大化问题可以被转化成为原网络上的最小割图分割问题，并应用多层次图分割的Kernighan-Lin算法[9]来解决上述最小割图分割问题。

本文另外一个贡献在于，创新性地将模块度理论和统计推理算法(例如随机块模型[10-11]及其度修正变体[12])相结合。统计推理算法首先假设了一些用于产生社区结构的潜在概率模型，进而估计模型的参数。实际上，基于模块度的算法和此类基于统计推理模型的算法均可以视为最优化问题，因此我们尝试证明二者之间的联系。所以，统计推理模型在本文提出的算法中扮演着重要角色：

(1) 在证明过程中，统计推理模型可以被转化成为模块度最大化问题中的零模型(null model)[12]。

(2) 统计推理算法的核心思想是通过最大化似然函数(likelihood)来产生一个合理的目标函数，因此，我们修改这个目标函数以应用于我们的最优化策略中。

简言之，本文提出的算法首先通过执行多层次最小割图分割算法，得到一个包含众多社区结构的候选集合；然后使用度修正随机块模型的目标函数，从候选集合中选择目标函数值最大的社区结构作为最终结果。据悉，我们首创性地探寻模块度理论、统计推理模型和传统图聚类/图分割算法三者之间的内在联系，虽然本文算法在时间复杂度方面依然有很大提升空间(文献[8]也面临同样挑战)，但是本文算法在真实世界网络和人工生成网络的实验中均得到了很高的准确率和稳定性。

本文的内容组织如下：第二节将总结相关工作；第三节重点分析度修正随机块模型的原理；在第四节中，我们将详细分析模块度最大化算法和最小割图分割算法之间的关系，并提出我们的算法；第五节和第六节将阐述实验和相关结果及结论。

2 相关工作

作为聚类质量的评价指标，模块度被文献[1]引入到社区发现研究中，并凭借其直观高效的特点，逐渐成为社区发现研究的常用度量方式。文献[7]提出的贪婪的基于模块度的社区发现算法CNM，已成为当今使用最为普遍的算法。该算法从嵌套的堆栈中迭代地选择和合并能够产生最大模块度增益的最优节点对，直至没有此类节点对能够提高模块度为止。此后，作为CNM的变体，一系列针对有权重网络和有向网络的计算模块度的算法相继被提出；此外，基于其他理论的诸多算法也被提出，例如计算网络图的Laplacian特征向量的算法[13]等。近年来，包括随机块模型[10]及其度修正变体[11]在内的统计推理算法，凭借其优良的性能吸引着越来越多的研究兴趣。

不难发现，社区发现与图分割/图聚类有着密切关系，但是二者之间依然存在着一定差异[6]。图分割是人工智能领域被深入研究的课题[14-16]，旨在将网络中的节点划分成一些指定规模(并不要求规模相等)的分组，并且确保分组之间连接边的数量最小。其中有两类算法占据着主导地位：基于网络图Laplacian特征向量的谱二分析法，以及使用贪婪策略不断优化社区外部连接边和内部连接边进而不断改善初始划分的Kernighan-Lin算法[16]及其多层次变体[9](见图1)。目前，学界已有不少利用(归一化)最小割图分割算法进行社区发现的研究[17]，但是对于模块度最大化与最小割图分割的关系的研究尚属少数[18]。文献[18]意在证明归一化模块度最大化问题可以转换为RatioCut谱聚类问题，但是无法精确证明二者之间的等价关系。

3 度修正的随机块模型

原始的随机块模型是一个用于网络社区的产生式模型，但是由于忽略了节点度的多样性，导致其很难被应用于真实世界网络。为了解决上述问题，度修正随机块模型(degree-corrected stochastic block model)[12]为每个节点i添加了一个参数θi用于控制节点i的度的期望值，这使其能够适应任何度分布。

对于网络G(V,E),V和E分别表示该网络全部n个节点的集合和全部m条边的集合，k表示社区的数量。Aij表示G(V,E)的邻接矩阵的元素，其值等同于节点i和节点j之间边的数量，且Aii=0。ωrs是一个k×k维对称矩阵的元素，控制着社区r和社区s之间的连接边。我们将Aij的期望值设定为θiθjωgigj[12]，其中gi表示节点i所隶属的社区。综上所述，生成网络G(V,E)的似然度函数为式(1)。

其中，ki是节点i的度；κs是社区s所有节点度的总和；mrs是连接社区r和社区s的边的数量，其定义如式(3)所示。

其中，δgigj是KroneckerDelta。将θ和ω的值带入式(1)，经过适当改写，我们便得到了只依赖于社区结构轮廓的似然函数，并取对数得

因为统计推理算法通常被用作评估社区发现算法的基准算法，所以我们不妨利用式(4)作为判别社区划分是否合理的目标函数

4 基于最小割图分割的社区发现算法

文献[1]所定义的模块度概念，被广为认可和使用，而近来来关于社区发现的研究也大多集中在模块度最大化问题。本章将证明，模块度最大化问题可以被转化成原网络最小割图分割问题。

给定以下条件：

(1) 一个拥有n个节点和m条边的网络G(V,E),V和E分别代表上文所定义的节点集合和边集合；

(2) 包含k个社区的一个划分P=P1,…,Pk；

(3) 一个在原网络节点集合V上的随机网络分布为G。

随机网络分布G有很多选择方式[19]，具体如下。

(1)Erdös-Renyi模型：原始的随机块模型与Erdös和Renyi提出的随机图模型[20]有密切的内在联系[12]，但是这个模型极易产生不符合实际的网络(度分布服从泊松分布)，甚至产生没有社区结构的网络。

(2)Chung-Lu模型：为了避免上述问题，模块度经常使用另外一种固定度期望序列使之与被观察网络一致的模型来定义。这种意义下，度修正的随机块模型与Chung和Lu所研究的模型[21]有关。

为了简化描述，我们定义

为划分P所对应的割规模。我们首先考虑最简单的情况——二分问题(即k=2)，式(6)可以被改写成

对于式(8)中随机网络分布G的选定，我们将分别考察原始随机块模型及其度修正变体。

4.1 将原始随机块模型作为G的情况

重写式(8)得

如果我们使用w12来表示社区1和社区2之间的边的数量期望值，那么

考虑到

其中，n1和n2分别表示社区1和社区2中节点的数量，则

因此模块度最大化问题可以被进一步重写为

至此，式(6)所代表的原始问题，已经被转化成了计算公式(15)。

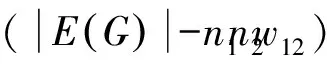
4.2 将度修正的随机块模型作为G的情况

去掉式(8)中的常数项m，我们可以得到

在度修正随机块模型中，我们有

其中，w11和w22分别表示社区1和社区2内部边数量的期望值。并且有

相似地，可得

至此，式(6)所代表的原始问题，已经被转化成了计算式(21)。

式(21)与式(15)十分相似，原始的模块度最大化问题也被映射成为一个带有附加项的最小割图分割问题。所以，综合考虑式(15)和式(21)，本文首先固定随机网络分布G，执行以社区结构为自变量的最小化；然后，固定社区结构，执行以G为自变量的最小化。

我们可以执行下述在社区发现研究中常用的贪婪策略[7]来完成对社区规模n1和n2的选择。假设我们并不区分社区的类别，即我们只需要将所有节点划分进两个不同的社区，而并不关心某个节点具体属于哪个社区。如果网络中节点总数n是偶数，那么有n/2+1种对两个社区的规模的选择方式：一种极端的选择方式将所有节点放入某一个社区中，另一种极端的选择方式将所有节点均分到两个社区中，其他的选择方式介于上述两种极端选择方式之间。相似地，如果n是奇数，则会有(n+1)/2种对两个社区规模的选择方式。上述所有选择构成一个单一参数(参数为社区规模)的候选集合；对于每个选择均对应一个标准的最小割图分割问题，因此很多启发式算法[14-16]可以应用于此，本文使用多层次的Kernighan-Lin算法[9]解决该最小割图分割问题，并得到相应候选解(即候选的社区结构)。此时，因为这里使模块度全局最大的候选解应同样满足使式(4)取得最大值，所以我们将每个候选解带入式(4)并计算，从计算得到的目标值中选择最大值对应的候选解作为最终结果。上述将网络划分为两个社区的算法可以很简单地扩展到多社区划分的情况，方法如下：我们首先使用上述算法将网络分成两个网络，然后递归地将各个子网络继续划分成两个社区，以此类推[13]；对于某个子图，如果其任何划分都不增加整个网络的模块度，那么这个子图将被保留成为一个社区而不再被继续分割。

基于文献[9]中的分析，本文提出的算法将包含n个节点和m条边的网络划分成两个社区的时间复杂度为O(n2)；当划分为k个社区的时候，只需要执行d次上述计算即可，其中d是树状图的深度(在二分树中，log2k≤d≤k)。因为本文提出的算法是一个创新性的尝试和证明，所以与现有算法(如算法[7])相比，其计算时间并不具备优势，依然有很大改进空间(这种降低时间复杂度的挑战同样也是文献[8]所面临的)。因此在降低时间复杂度方面对算法进行改进，将是未来工作的方向之一；但是实验结果显示，该算法对于发现社区结构具有很高的准确率。

5 实验和结果分析

本节中，我们在真实世界网络和人工生成网络上，分别测试本文算法(记为MC)的性能并与其他算法进行比较，实验证明其取得了良好的实验结果。其中，真实世界网络可以体现算法在现实条件下的性能，而人工生成网络可以在已知社区结构设定和受控条件下测试算法发现社区结构的能力。本文实验部分修改和应用基于多层次图分割策略的图分割工具包METIS-5.1.0*http://glaros.dtc.umn.edu/gkhome/metis/metis/download，主要采用的度量方法是归一化互信息(normalizedmutualinformation,NMI)[22]及其变体(variantnormalizedmutualinformation，VNMI)。

本文实验所使用的网络的社区结构均已知，这使得我们可以度量被算法所正确划分的节点的数量。所以，本文重点关注：真实的社区结构和算法所产生的社区结构之间的差异。将上述两种社区结构均视为随机变量(分别记为A和B)，NMI定义如下：

5.1 真实世界网络实验

我们将本文算法应用在了一系列不同规模的真实世界网络，算法均产生了与先验知识一致的社区结构。这里，我们重点介绍其中三个真实世界网络的实验细节。

第一个实验网络是“KarateClub”网络[23]，该网络表示一所美国大学中拥有34个成员的空手道俱乐部中的人际关系交互情况。由于一次争吵，这个俱乐部的成员被划分成为两个部分，因此这个网络为二分算法提供了良好的实验素材。图2展示了本文算法在“KarateClub”网络上的实验结果。结果显示，本文算法准确地识别出了已知社区结构，除了错分位于两个社区边界的编号为10的节点——该节点在很多其他的算法中也经常被错误分类[12]，主要因为该节点连接到两个社区的边的数量相同。第二个实验网络是“BottlenoseDolphins”网络。图3 展示了本文算法在 “BottlenoseDolphins”网络的实验结果。该网络包含了位于新西兰的62只海豚，是通过观察它们之间交互的频繁程度而建立的网络[24]。本文算法首先将这个网络分成两个大的子网络，其中较大的一个随后又被分成两个较小的子网络。

图2 “Karate Club”网络实验结果

图3 “Bottlenose Dolphins”网络实验结果

第三个网络是“AmericanPoliticalBlogs”网络。“AmericanPoliticalBlogs”网络[25]由2004年美国总统大选期间政治类博客及其链接信息组成，这些博客中的前758个是支持共和党的，而剩下的732个博客是支持民主党的。表1显示，本文算法应用于全部1 490个节点的情况下，NMI值只有0.500 502(错分164个节点)；但是如果去掉原图中225个孤立节点而只考虑原图的联系密切的主要部分节点(1 265个节点)及其连接，NMI值上升到0.720 525，这与文献[12]的实验结果十分接近。

表1 “American Political Blogs”网络实验结果

5.2 人工生成网络实验

为了与其他(基准)算法进行比较，我们将本文算法分别应用到基于度修正随机块模型(DCM)[12]和Lancichinetti-Fortunato-Radicchi(LFR)基准[26]所产生的人工生成网络上。

5.2.1 DCM人工生成网络实验

效仿文献[12]，本文按照如下的定义来选择ωrs，从而产生基于DCM的人工生成网络。

在第一组DCM人工生成网络实验中，每个网络均含有100 000个节点，以及两个等规模的社区，并且每个社区的度的平均期望值均为20。在选定社区结构、所有节点度的期望值(公式(2)中的θi)和ωrs的取值之后，我们按照如下方法来生成网络：首先对于每对社区r和s，产生一个服从泊松分布(均值为ωrs)的边的数量值，然后根据θi将所有边附着在节点i上。本文提出的MC、原始随机块模型(记为SBM)和度修正随机块模型(记为DCM)被应用在第一组实验网络上进行性能对比。对于SBM和DCM这两个模型，我们均采用随机设定(后缀为R)和种植设定(后缀为P)分别进行初始化，分别进行10次独立运行，并从中选择最好的结果展示出来。

图4将NMI值作为参数λ的函数值，每个数据点代表了在100个等条件生成网络上的平均值。图4(a)显示，随着λ从0开始逐渐增长，虽然因为此时的网络还处于比较随机的状态，所有的算法均未能产生比较合理的社区结构，但是本文算法性能优于其他算法，一方面是因为最小割图分割思想有效地将社区发现问题还原到了图论问题的本质，另一方面是因为本文算法引入的穷举策略，能够遍历当前参数设定条件下所有可能的社区划分。值得注意的是，本文的算法为每个候选社区结构均计算“目标值”[见式(4)]，但是只有拥有最大“目标值”的社区结构才会被选中成为最终结果，所以在最终结果的NMI值和所有候选的社区结构中最大的NMI值之间存在一个“间距”：通过实验我们发现，当λ的取值接近于0的时候，上述“间距”比较大；而当λ继续增加，“间距”开始下降。这种现象很直观地解释了以下问题：当网络中社区划分越明确，传统图分割算法对于社区划分结果的置信度越高；同时，这种“间距”下降，也证明了本文引入度修正随机块模型的似然函数的有效性。此外，当λ超过中值，MC和DCM的曲线基本重合，说明我们的结果达到了当前最优的基准效果。而对于未进行度修正的SBM，即使λ的取值已经超过中值，也依然未能产生合理的社区结构。

另外一组基于DCM人工生成网络的实验采用的生成网络更加复杂和贴近现实网络。社区规模与度的平均期望值与上一组实验相同，不同之处在于，本组实验设定社区1的度分布服从幂律分布——复杂网络的显著特征之一，并且取幂指数γ=2.8；设定社区2的度分布为均值为20的泊松分布。图4(b)证明了本文算法具有良好的稳定性：MC在λ很小的情况(即网络社区划分不明确，甚至是几乎随机的网络)下依然能够体现出不错的性能。这是因为MC能够仅仅依靠节点的度信息对绝大部分节点进行分类。相反地，在λ≤0.2的情况下，DCM的正确率几乎为0，仅略微优于原始的SBM。当λ处于插值的中值阶段(0.5≤λ≤0.7)时，DCM性能优于本文提出的MC，但是在λ取其他值时，MC依然优于DCM。换言之，当每条边都有几乎相同概率从随机网络和种植网络中选择的时候，DCM准确率的提升速度要快于MC的准确率。特别地，本组实验社区1中更为接近现实复杂网络中度的幂律分布，使SBM的性能远差于其在上一组实验的性能，这是因为SBM产生的网络中，节点的度服从泊松分布，而泊松分布不符合真实世界网络，因此SBM无法有效拟合观测网络。比较上述两组DCM人工生成网络实验，我们不难发现，现实网络更有助于本文算法发挥其性能优势。

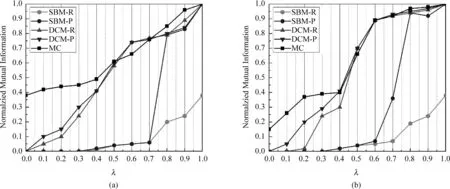
图4 基于DCM的人工合成网络的实验

5.2.2LFR人工生成网络实验

为了测试算法在一系列大跨度、宽范围的结构化网络特征下的性能，我们使用LFR基准网络进行实验。LFR综合考虑了度和社区规模的多样性，是社区发现研究领域经常被使用的比较符合现实网络特征的基准网络。

本文主要讨论下述三个主要的用于生成网络的参数，对不同算法的性能影响： (a)聚合参数μ，类似于上述DCM人工生成网络实验中的参数λ；(b)节点度的平均值〈k〉；(c)网络所包含的节点总数N。

首先，本文与文献[28]进行对比实验。我们使用相同的实验网络设定，实验包括两种不同的网络规模(1 000个节点和5 000个节点)，度的平均值为20。图5(a)呈现了本文算法的实验曲线，每个数据点均代表100个等条件网络实验结果的平均值。其中，后缀S和B分别表示较小的社区规模(每个社区包含10～50个节点)和较大的社区规模(每个社区包含20～100个节点)。通过实验结果对比，本文算法比文献[28]所分析的算法更有竞争力；相似地，当μ由0.6增长为0.7的时候，曲线出现了快速下降。

图5(b)和图5(c)分别展示了节点度平均值〈k〉和节点总数N对算法性能的影响。通过实验我们发现，节点数量对于算法性能的影响有限；然而节点度平均值却对准确率有着显著影响，在节点度的变化过程中，几乎所有算法都遭受过NMI值的巨大损失，而大部分算法的NMI值在度平均值取值约为25的时候达到峰值。

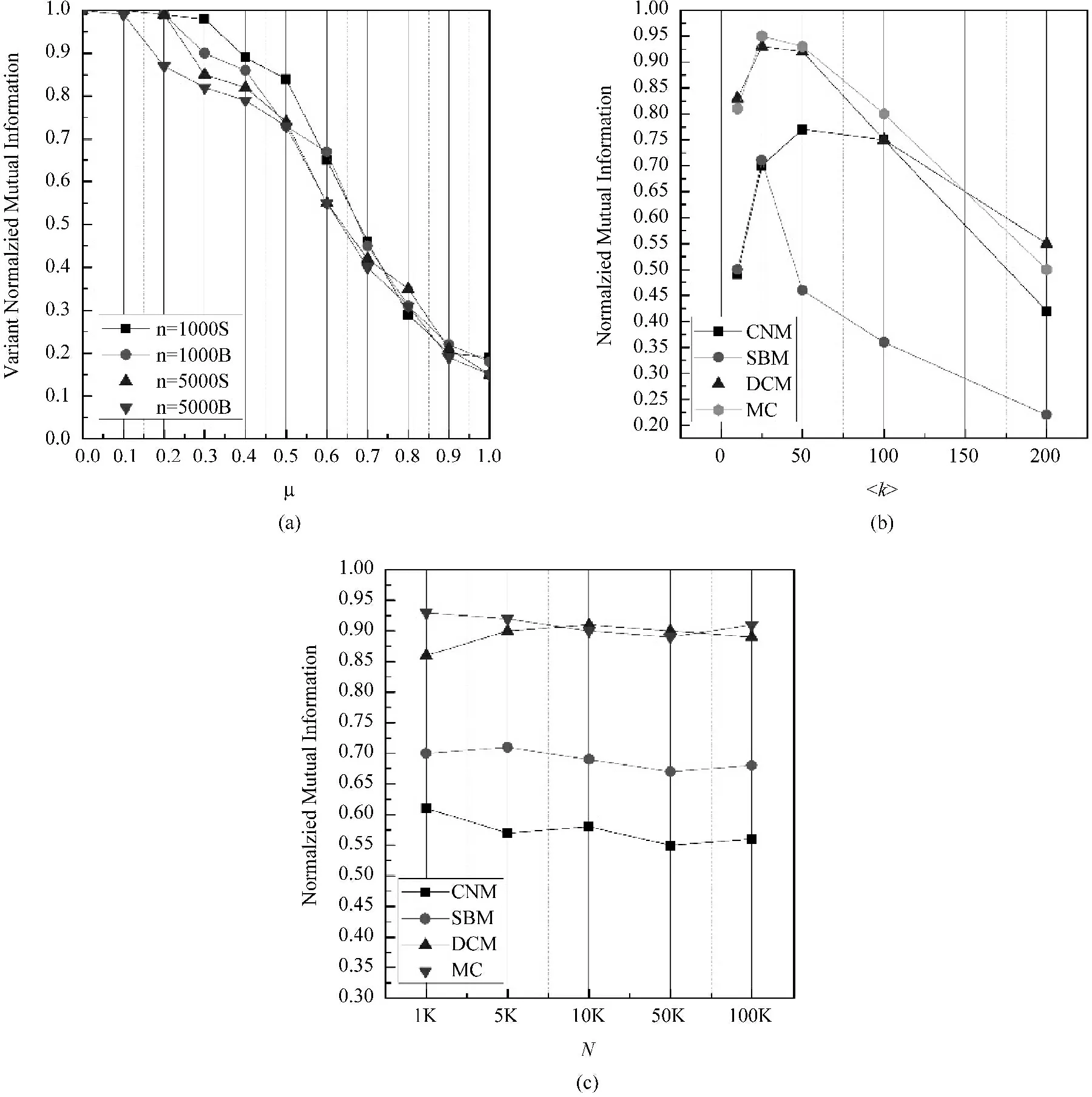
图5 基于LFR的人工生成网络的实验

6 总结

社区发现长久以来一直吸引着学者们的研究兴趣，诸如基于模块度算法、统计推理模型算法和基于传统图聚类/图分割算法等不同类型算法被相继提出。我们始终认为，在这些不同的理论之间一定存在某些内在联系。所以，本文进行了一个创新性的尝试，旨在探索并发现这些理论之间的潜在联系。本文证明了模块度最大化问题可以被转化成在原网络上的最小割图分割问题，因此所有高效的最小割图分割算法均可以被应用于本文提出的算法中。此外，本文将模块化理论和当今比较流行的统计推理模型进行充分结合，将后者转化成为模块度最大化问题中的零模型，并将其目标函数应用在我们的最优化策略中。基于上述证明和讨论，本文提出了一种新的基于网络拓扑结构的社区发现算法。

我们在不同规模(节点数量级最高达到百万级)的真实世界网络和人工生成网络上测试了本文提出的算法。实验结果显示，本文算法在发现社区结构的能力方面具备高效性和稳定性；尤其是在诸如幂律分布此类有着强烈不均衡度分布的网络中，本文算法依然表现出良好的性能。除了“大规模”特性，现实社交网络的另一个重要特征就是“动态”特性。因此，我们的后续研究将重点关注解决在线或者动态社区发现问题；同样，我们将会继续完善本文算法，以进一步降低其时间复杂度。

[1]NewmanMEJ,GirvanM.Findingandevaluatingcommunitystructureinnetworks[J].PhysicalReviewE, 2004, 69(2): 026113.

[2]Fortunato,S.Communitydetectioningraphs[J].PhysicsReports. 2010, 486(3): 75-174.

[3]ZhouTC,MaH,LyuMR,etal.User-Rec:auserrecommendationframeworkinsocialtaggingsystems[C]//Proceedingsof24thAAAIConferenceonArtificialIntelligence.Atlanta,USA:AAAIPress, 2010: 1486-1491.

[4]WengJ,LeeBS.EventDetectioninTwitter[C]//Proceedingsof5thInternationalAAAIConferenceonWeblogsandSocialMedia.Barcelona,Spain:AAAIPress, 2011: 401-408.

[5] 靳延安,李瑞轩,文坤梅,等. 社会标注及其在信息检索中的应用研究综述[J]. 中文信息学报,2010,(4): 52-62.

[6]PapadopoulosS,KompatsiarisY,VakaliA,etal.CommunitydetectioninSocialMedia[J].DataMiningandKnowledgeDiscovery, 2011, 24(3): 515-554.

[7]ClausetA,NewmanM,MooreC.Findingcommunitystructureinverylargenetworks[J].PhysicalReviewE, 2004, 70(6): 066111.

[8]NewmanMEJ.Communitydetectionandgraphpartitioning[J].EPL(EurophysicsLetters), 2013, 103(2): 28003.

[9]KarypisG,KumarV.Afastandhighqualitymultilevelschemeforpartitioningirregulargraphs[J].SIAMJournalonScientificComputing, 1998, 20(1): 359-392.

[10]CondonA,KarpRM.Algorithmsforgraphpartitioningontheplantedpartitionmodel[J].RandomStructuresandAlgorithms, 2001, 18(2): 116-140.

[11]AiroldiEM,BleiDM,FienbergSE,etal.Mixedmembershipstochasticblockmodels[J].TheJournalofMachineLearningResearch, 2008, 9: 1981-2014.

[12]KarrerB,NewmanMEJ.Stochasticblockmodelsandcommunitystructureinnetworks[J].PhysicalReviewE, 2011, 83(1): 016107.

[13]NewmanMEJ.Findingcommunitystructureinnetworksusingtheeigenvectorsofmatrices[J].PhysicalReviewE, 2006, 74(3): 036104.

[14]FjallstromP.Algorithmsforgraphpartitioning:asurvey[J].LinkopingElectronicArticlesinComputerandInformationScience, 1998, 3(10) 123-128.

[15]FiedlerM.Algebraicconnectivityofgraphs[J].CzechoslovakMathematicalJournal, 1973, 23 (98): 298-305.

[16]KernighanBW,LinS.Anefficientheuristicprocedureforpartitioninggraphs[J].BellSystemTechnicalJournal, 1970, 49: 291-307.

[17]FlakeGW,TarjanRE,TsioutsiouliklisK.Graphclusteringandminimumcuttrees[J].InternetMathematics, 2004, 1(4): 385-408.

[18]WhiteS,SmythP.Aspectralapproachtofindcommunitiesingraphs[C]//ProceedingsofSIAMConf.onDataMining. 2005: 76-84.

[19] 马力,焦李成,白琳,等. 基于小世界模型的复合关键词提取方法研究[J]. 中文信息学报,2009,(3)： 121-128.

[20]ErdösP,RenyiA.Onrandomgraphs[J].Publ.Math, 1959, (6): 290-297.

[21]ChungF,LuL.Connectedcomponentsinrandomgraphswithgivenexpecteddegreesequences[J].AnnalsofCombinatorics, 2002, 6(2): 125-145.

[22]FredALN,JainAK.Robustdataclustering[C]//2003IEEEComputerSocietyConferenceonComputerVisionandPatternRecognition.Madison,Wisconsin,USA:IEEEPress, 2003:II-128-133.

[23]ZacharyWW.Aninformationflowmodelforconflictandfissioninsmallgroups[J].JournalofAnthropologicalResearch, 1977, 33(4): 452-473.

[24]LusseauD,SchneiderK,BoisseauOJ,etal.ThebottlenosedolphincommunityofDoubtfulSoundfeaturesalargeproportionoflong-lastingassociations[J].BehavioralEcologyandSociobiology, 2003, 54(4): 396-405.

[25]AdamicLA,GlanceN.Thepoliticalblogosphereandthe2004U.S.election[C]//Proceedingsof3rdInternationalWorkshoponLinkDiscovery.NewYork,NewYork,USA:ACMPress, 2005: 36-43.

[26]LancichinettiA,FortunatoS,RadicchiF.Benchmarkgraphsfortestingcommunitydetectionalgorithms[J].PhysicalReviewE, 2008, (78): 046110.

[27]ChungF,LuL.Theaveragedistancesinrandomgraphswithgivenexpecteddegrees[J].ProceedingsoftheNationalAcademyofSciencesoftheUnitedStatesofAmerica, 2002, 99(25): 15879-15882.

[28]LancichinettiA,FortunatoS.Communitydetectionalgorithms:Acomparativeanalysis[J].PhysicalReviewE, 2009, 80: 056117.

CommunityDetectionBasedonMinimum-CutGraphPartitioning

WANG Yashen, HUANG Heyan, FENG Chong

(Beijing Engineering Research Center of High Volume Language Information Processing and Cloud Computing Application, School of Computer, Beijing Institute of Technology, Beijing 100081, China)

This article demonstrated that modularity maximization issue could be transformed into minimum-cut graph partitioning problem, and proposed an efficient algorithm for detecting community structure. Meanwhile, we combined the modularity theory with popular statistical inference method in two aspects: (i) transforming such statistical model into null model in modularity maximization; (ii) adapting the objective function of statistical inference method for our optimization. The experiments we conducted show that the proposed algorithm is highly effective and stable in discovering community structure from both real-world networks and synthetic networks.

community detection; modularity; minimum-cut graph partitioning