基于CZT的光伏发电系统间谐波检测方法研究

程 琳， 田 彦， 李奕铭

（1.国网安徽省电力公司培训中心，安徽 合肥 230022；2.安徽电气工程职业技术学院，安徽 合肥 230051）

基于CZT的光伏发电系统间谐波检测方法研究

程 琳1，2， 田 彦1，2， 李奕铭1，2

（1.国网安徽省电力公司培训中心，安徽 合肥 230022；2.安徽电气工程职业技术学院，安徽 合肥 230051）

在光伏发电系统中，各种电力电子设备的广泛应用，使得含光伏发电系统的大电网中非线性、冲击性和波动性的负荷大大增加，从而使得电能质量的污染也变得越来越严重。该文针对光伏发电系统电能特征进行研究，在研究常用窗函数频域特性及加窗插值算法对频谱泄露和栅栏效应的改进方法的基础上，提出基于Rife-Vincent（III）窗函数的改进算法与实现步骤。通过仿真，改进算法使得微弱间谐波幅值检测精度得到提高。

光伏发电系统；间谐波检测；线性调频Z变换；双谱线；Rife-Vincent（III）窗

0 引 言

随着全球经济和世界人口增长，环境污染、气候变化等问题日益突出，严重威胁人类生存和可持续发展，传统能源发展方式已难以为继。统筹解决能源和环境问题，破解经济社会发展瓶颈，已经变得十分紧迫。新世纪以来，以电为中心，清洁化为特征的能源结构调整加快推进，清洁能源的大规模开发成为世界主要国家的共同选择[1-2]。绝大部分清洁能源只有转化为电能才能高效利用。而电能作为优质、清洁、高效的二次能源，能够替代绝大多数能源需求，是未来最重要的终端能源。构建分布式光伏发电能源接入区域电网不仅是能源技术的革新，也是一次能源生产、消费以及政策体制变革。

光伏发电技术和通常的发电技术相比，它容易受光照强度、温度等一系列不可预测的因素影响，输出功率存在随机性、波动性、间歇性，会引起电压波动、电压闪变以及频率波动等一系列电能质量问题[3]。光伏发电能量的传递和转换都是建立在电力电子技术的基础上，逆变器则是整个系统的关键所在。逆变器采用电力电子器件技术将所发出的直流电转变为能供用户使用的交流电，在逆变的一系列进程中就会产生数量巨大的各次谐波，而且伴随着光伏系统的不确定因素，系统内谐波的波动性较大，从而对用电装置带来严重的损害[4]。目前把含有供电系统设计运行频率（即简称工频，通常为50 Hz或60 Hz）整数倍频率的电压或电流定义为谐波。而把含有供电系统设计运行频率非整数倍频率的电压或电流定义为间谐波[5]。在电力系统中，间谐波的产生是无可避免的，间谐波的存在对电网或者系统而言危害性比较严重，不仅仅影响电力的供电质量，而且还会让计量电能参数的仪器仪表出现计数问题，造成严重的计数误差，继电保护装置误动的严重问题。对于任何一个电能质量问题，只要出现的情况加重了，也会对整个系统乃至用户的设备的安全运行造成不可预计的后果。

目前，在电力系统中，对于间谐波的检测方法比较常用的有傅里叶变换法、小波分析算法[6-7]等。文献[8]给出了基于短时傅里叶变换的间谐波测量方法，文献[9]给出了用于间谐波检测的谱分析方法，即采用自回归模型分析和特征分解法。相关谱分析方法及其改进算法能够比较有效地检测出间谐波的参数，但是该方法比较容易受到外界噪声的影响，如果外界的噪声信号比较强的话，该方法就没法对间谐波进行检测。而在电网中，各种噪声信号都是存在的，因此要使用谱分析方法分析间谐波就要提前对需要检测的信号进行滤除噪声波的处理才行。随着人工智能的发展，神经网络检测法也被用于检测间谐波[10-11]。虽然在检测精度上有所提高，但是人工神经网络检测法需要根据信号源确定一个数学模型，造成大量的计算，是一个比较复杂的方法。

本文在光伏发电系统电能特征基础上分析间谐波特点，采用了基于线性调频Z变换的方法进行间谐波检测。

1 光伏发电系统中间谐波信号特点

光伏发电系统是由多个地理位置分散的光伏发电单元组成，通过光伏单元共同工作来给负载供电并将多余的电能汇入电网，同时还要保证整个系统在工作状态下的稳定。目前，主要使用的光伏发电半导体材料为硅，也可根据制造工艺不同区分为单晶硅、多晶硅和非晶硅，太阳能电池即由这些硅材料制成，从而得以利用光电效应将太阳能转换为电能。

发电过程中，太阳能光伏电池板首先将光能转化为直流电能，然后直流电流经过逆变器转化为频率、电压满足并网要求的交流电或者适合负载需求的交流电。将光伏发电系统接入常规电网并网发电是光伏发电进入商业化应用的必经之路，同时也是将来光伏发电的主流趋势。实际应用时，一般利用光伏发电阵列组合进行大规模的发电，因为单块电池板的发电容量较小且电压较低（单块太阳能电池的电压在0.48～0.5V之间），此电压很小，所以输出的功率也只有3～4W。电网系统拓扑结构如图1所示。

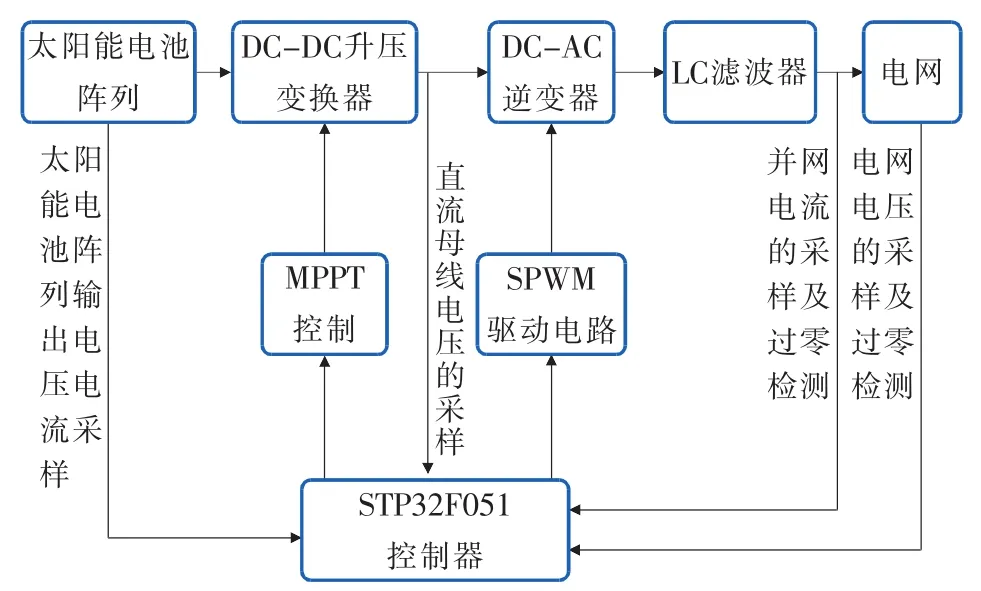
图1 光伏系统发电模型

将太阳能光伏发电系统并入外部大电网时，首先需要通过逆变器把直流电转化为满足并网要求的交流电，然后经过变压器升压后就可接入配电网。光伏发电机组的大量接入电网，导致电压和电流波形发生畸变，电压和电流中的谐波和间谐波不断增加。此时，电压和电流信号是呈非正弦形式的周期性变化，可分解为一系列正弦波之和，其中，整数倍基波频率的正弦波定义为谐波，非整数倍基波频率的正弦波定义为间谐波。当变流器两侧交流信号频率不相同时，不同频率成份会通过开关调制作用产生间谐波。这些间谐波的频率为

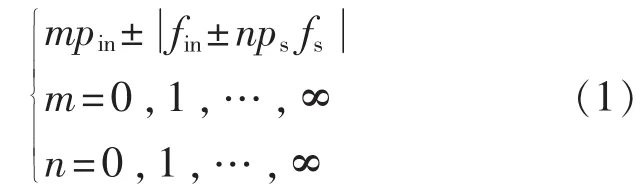
式中：pin——整流器的脉冲数；

ps——逆变器的脉冲数；

fin——供电系统频率；

fs——电动机运行频率。

同时电网中的波动性负荷会向电网注入间谐波电流，引起电网电压波动。

2 基于线性调频Z变换的间谐波信号处理方法

2.1 线性调频Z变换的原理

快速FFT算法是常用的电网信号分析方法，FFT算法实质上都是序列Z变换在单位圆上的等间隔采样。然而工程中有时只对信号的某一段频带感兴趣，在这种情况下，如果采用FFT算法，则需要在窄带频带内外都增加抽样点数，提高分辨率，增加了窄带频带外不需要的计算量。线性调频Z变换（chirp Z transform，CZT）是有效的频率细化方法。采用FFT计算的N点的频谱实际上是Z平面单位圆上的N点等间隔取样，那么CZT计算就是在Z平面螺旋线周线上的Z变换的等间隔采样的结果。设x（n）表示N点序列，0≤n≤N-1，Z变换为

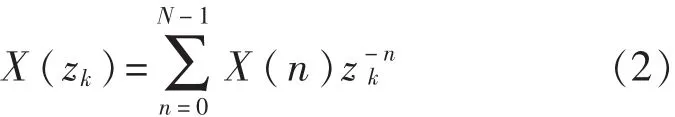
式中 X（n）（n=0，1，…，N-1）是长度为 N 的有限长序列。分析Z平面上M点频谱的采样值，可令zk=AW-k，（k=0，1，…，M-1）则 CZT 变换为

式中 A=A0exp（jθ0），W=W0exp（-jφ0），A0表示起始采样点的矢量半径长度，θ0表示起始点相角，W0表示路径的伸展趋势，φ0表示相邻采样点的角度间隔。其余的采样沿螺旋周线以φ0为等间隔进行采样即可以得到其余的采样点。

式中f0、fh、fs分别为信号的起始频率、截止频率和采样频率，则序列X（n）的CZT结果即为该序列在所选频段内的离散傅里叶变换的结果。由于传统的方法形成CZT结果的速度比较慢，因此本文采用了Bluestein算法生成CZT：

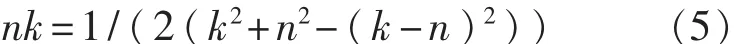
则有

CZT算法要求整周期采样，但电网信号频率通常会在额定频率附近波动，实现完全同步采样很难。采用普通CZT算法会给光伏发电系统电网间谐波分析带来误差，需要采用加窗插值算法提高分析精度。

2.2 基于Rife-Vincent（III）窗的双谱线修正

设fs为采样频率，Ts为采样间隔，对一个单一频率的信号x（t）进行离散采样的结果为

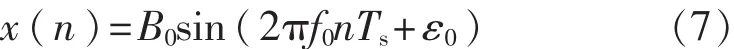
式中f0、B0、ε0分别为这个单一信号的频率、幅值和初相位。对信号所加窗函数的时域表达式为w（n），则加窗后该单一信号序列x（n）的CZT变换结果为

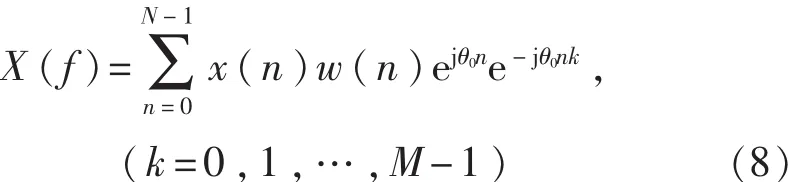
由奈奎斯特定理可知，采样频率高于2倍的信号最高频率，因此本文选频带（0，fs/2）进行线性调频Z变换分析，那么式（8）可以简化为

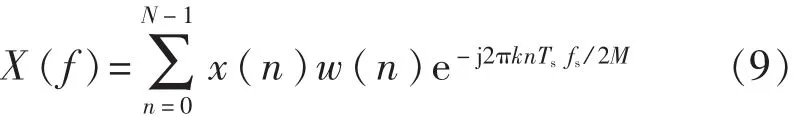
然后采用欧拉公式对式（9）式进行展开后得到：

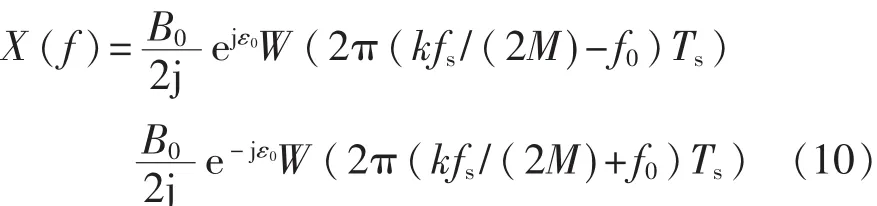
如果忽略负频点-f0处频峰的旁瓣影响，N为数据截取长度，CZT的输出序列M=N/2，则该方法的分辨率为 Δf=fs/（2M），那么 Δf=fs/N，那么此时的 CZT 的结果等价于所选频段（0，fs/2）内的DFT的结果，从而加窗信号的离散频谱的表达式为

在实际的采样过程中很难做到对间谐波的进行同步采样的，而且频率的峰值频率f0一般不落在离散谱线频率点上。根据双谱线的修正算法，设峰值点左右两侧谱线分别为第k1条谱线和第k2条谱线，那么其谱线的幅值为 y1=|X（k1Δf）|和 y2=|X（k2Δf）|，其中k1和k2是峰值点附近最大和次最大的谱线，且k1≤k0≤k2=k1+1。

设 β=（y2-y1）/（y2+y1），那么将 Ts=1/（NΔf）代入 β可以得到：

再设α=k0-k1-0.5，那么α的取值范围为（-0.5，0.5），上式变换为

由于N较大，因此通常采用多项式逼近的方法求取了式（13）的反函数 α=g-1（β）。 对于峰值点处得幅值的修正，采用对k1和k2进行加权平均，其计算公式为

当N较大时，式（14）可以化简为

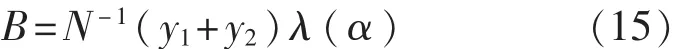
λ（α）采用同样的多项式逼近法进行求取，α的取值范围是（-0.5，0.5）。

在进行频谱分析时要求所采用窗函数的主瓣宽度窄、旁瓣幅值衰减快的，那么根据这个特点，本文选取了Rife-Vincent（III）窗来截取间谐波的信号。设逼近多项式的最高阶的阶数为7，利用多项式拟合求取 g-1（β）和 λ（α）的系数，可以忽略多项式中对结果影响很小的一些系数项，那么当i=1或2时得到的修正公式为

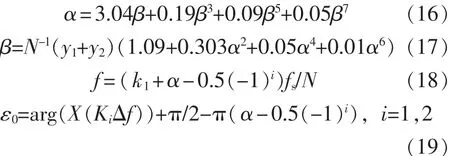
2.3 算法步骤

加窗插值CZT算法通过加窗减少频谱泄漏，通过插值消除栅栏效应引起的误差。算法步骤如下：

1）采样信号离散化。对时域连续信号进行采样与模数转换得到离散序列。

2）信号截断。对离散信号进行所需分析数据截断。

3）对截断离散序列采用 Rife-Vincent（III）窗卷积运算，并通过双谱线插值算法得到谐波频率周围离散频率谱线。

4）确定离散频谱中距离频率点处两条最大和次打频率谱线，并从式（4）中求解幅值，相位。

5）通过校正式（16）到式（19）计算相应间谐波参数。

Rife-Vincent（III）卷积窗双谱线插值间谐波分析算法流程图，如图2所示。

3 仿真分析

对于光伏发电系统，由于拥有DC/AC变换器等多种电力电子器件，使间谐波情况更加复杂。设采样信号为含有间隙波的多频信号：

图2 卷积窗双谱线插值变换间谐波分析算法流程

式中f为基波频率为50.2Hz，运用Maltlab 7.0.5进行实验仿真，取的是在频段（0，fs/2）进行的线性调频Z变换，信号的采样频率为1900Hz，采样长度N=1024点，设置的间谐波的参数如表1所示。

表1 间谐波信号参数设置

间谐波信号的频谱图如图3所示。可以得到：CZT算法增加了采样谱线的密度，减小了由于栅栏效应造成的误差，因此可以比较准确的求出信号的各个频率分量，其频率分量的估计值分别为：25.39，50.78，150.4，175.8，250，330.1，349.6，380.9，450.4 Hz，可以看出，各个频率的估计值和其实际值很接近的。

在得到CZT的谱线的信号的各个频率分量估计值后，然后通过比较各个分量两侧最大和次最大谱线从而确定k1和k2以及y1和y2，然后根据式（16）到式（19）来求取该间谐波的相应的幅值、频率和初相位角，该方法与双谱线插值线性调频Z变换的方法（即不加窗）进行比较。加窗后对间谐波的修正效果比较明显，具体的误差分析如表2所示。

图3 间谐波频谱图

表2 两种方法的相对误差分析表

从表中的数据比较中，可以看出，加窗后的线性调频Z变换的插值法比没有加窗的精度要高一些，当然个别的频率和幅值可能出现偏差，但是总体的精度是有所提高的，符合工程的要求的。没有加窗的间谐波的检测，频谱泄漏很严重，采用加窗的情况下，频谱的泄漏得到了有效的控制，测量精度得到提高。

4 结束语

间谐波是电力系统中广泛存在的一种特殊谐波，会对电能的质量造成了严重的污染，从某方面上说，其对电网及用电设备的危害远远大于谐波。本论文以间谐波为研究对象，提出采用基于插值的线性调频Z变换的方法进行间谐波检测与分析。并在此基础上提出了基于卷积Rife-Vincent（III）窗函数的改进算法,并给出算法实现步骤。通过Matlab仿真说明改进算法可以提高光伏谐波参数分析精度，为光伏发电系统谐波补偿装置的设计提供基本依据。通过算例仿真，在加窗的条件下，所测数据的精度有比较明显的提高，从而验证了基于加窗的插值的线性调频Z变换算法的有效性。

[1]丁明，王伟胜，王秀丽.大规模光伏发电对电力系统影响综述[J].中国电机工程学报，2014，34（1）：1-14.

[2]李碧君，方勇杰，杨卫东.光伏发电并网大电网面临的问题与对策[J].电网与清洁能源，2010，26（4）：52-59.

[3]曾正，赵荣祥，吕志鹏，等.光伏并网逆变器的阻抗重塑与谐波谐振抑制[J].中国电机工程学报，2014，34（27）：4547-4558.

[4]许德志，汪飞，毛华龙.多并网逆变器与电网的谐波交互建模与分析[J].中国电机工程学报，2013，33（12）：64-71.

[5]熊杰锋，李群，袁晓冬.电力系统谐波和间谐波检测方法综述[J].电力系统自动化，2013，40（11）：75-79.

[6]房国志，杨超，赵洪.基于FFT和小波包变换的电力系统谐波检测方法[J].电力系统保护与控制，2012，37（5）：125-133.

[7]钱昊，赵荣祥.基于插值FFT算法的间谐波分析[J].中国电机工程学报，2005，25（21）：87-91.

[8]郭辉，傅成华，何春芳.基于短时傅里叶变换的电压间谐波分析[J].电力系统通信，2008，29（4）：66-68.

[9]王波，杨洪耕.基于AR谱估计和插值FFT的间谐波检测方法[J].继电器，2006，34（4）：49-52.

[10]李波，张林利，王广柱，等.用于APF的神经网络自适应谐波电流检测方法[J].电力自动化设备，2004，24（5）：38-40.

[11]向东阳，王公宝，马伟明，等.基于FFT和神经网络的非整数次谐波检测方法[J].中国电机工程学报，2005，25（9）：35-39.

（编辑：刘杨）

Research on inter-harmonic detection method of photovoltaic power generation system based on CZT

CHENG Lin1，2，TIAN Yan1，2，LI Yiming1，2
（1.State Grid Anhui Training Center，Hefei 230022，China；2.Anhui Electrical Engineering Professional Technique College，Hefei 230051，China）

In photovoltaic power generation system，power electronic equipment is widely applied.The nonlinear， impulsive and fluctuating loads greatly increase in large power grid， and the pollution of power quality becomes more and more serious.The power characteristics of the photovoltaic power generation system are researched in this paper.The improved algorithm of the Rife-Vincent（III） convolution window is proposed based on research of the spectrum leakage and fence effect caused by the frequency domain characteristics of the common window function.By simulation，the detection accuracy for the weak inter-harmonic amplitude increased with improved algorithm.

photovoltaic power generation system；inter-harmonic detection；chirp Z transform（CZT）；dual spectral line；Rife-Vincent（III）window

A

1674-5124（2017）04-0105-05

10.11857/j.issn.1674-5124.2017.04.022

2016-09-21；

2016-11-02

国网安徽省电力公司培训中心科研项目（2016QC06）

程 琳（1975-），男，安徽无为县人，讲师，硕士，研究方向为电力系统及其自动化。