PMSM位置伺服系统鲁棒控制技术研究

杨瑞峰， 郭明明，张 鹏， 郭晨霞

（1.中北大学仪器与电子学院，山西 太原 030051；2.山西省自动化检测装备与系统工程技术研究中心，山西 太原 030051）

PMSM位置伺服系统鲁棒控制技术研究

杨瑞峰1，2， 郭明明1，2，张 鹏1，2， 郭晨霞1，2

（1.中北大学仪器与电子学院，山西 太原 030051；2.山西省自动化检测装备与系统工程技术研究中心，山西 太原 030051）

为提高永磁同步电机（PMSM）位置伺服系统的鲁棒抗扰特性，设计基于Backstepping控制、前馈控制和等价输入干扰（EID）估计的鲁棒抗扰控制策略。Backstepping控制是基于系统稳定性的控制方法，而前馈控制可以提升系统的响应速度，两者结合并设计合适的参数可以使系统在稳定的前提下具有一定的快速响应能力，再与具有良好扰动抑制功能的等价输入干扰估计器共同作用，可以有效提升系统的动态跟踪特性和抗干扰特性。通过计算机仿真实验对干扰作用下估计器的性能进行测试，得到良好的估计结果，验证估计器的可靠性；又通过仿真实验对系统进行阶跃响应测试、动态跟踪性能测试和鲁棒性测试，并与传统PID位置伺服控制进行对比分析，验证该鲁棒控制策略的有效性。

位置伺服系统；鲁棒控制；Backstepping控制；等价输入干扰估计；永磁同步电机

0 引 言

在工业自动化控制领域中，伺服系统是十分重要的一个分支，用于解决各种跟踪控制问题和定位控制问题，其中，永磁同步电机（PMSM）因具有优良的机械特性而被广泛用作伺服系统的执行机构，在机床、机械臂、机械转台等位置伺服控制系统中尤为普及[1]。随着现代电力电子技术和机械设计、制造技术的发展，对于伺服系统的性能要求也越来越高，永磁同步电机的非线性强耦合特性以及在工作过程中遇到的参数变化、不确定干扰等问题成为伺服系统性能优化的主要限制因素[2]，在保护措施不力的情况下甚至会损坏控制硬件和电机本体。因此，在许多国内外的相关文献中，自适应控制、滑模控制、H∞控制、模糊控制、神经网络等高级控制策略被越来越多地应用于伺服控制系统[3-7]，以获得更好的性能和更高的效率，这些算法各有优劣，适用于不同要求的伺服控制系统。

本文针对永磁同步电机位置伺服系统设计了一种简单高效的鲁棒抗扰控制策略，通过Backstepping控制方法保持系统的稳定性[8]，在此基础上引入前馈控制[9]，设计了复合鲁棒控制器来实现系统稳定性和响应速度的均衡，又通过等价输入干扰（EID）估计器来补偿系统受到的不确定扰动[10-12]，以提升位置伺服系统的鲁棒性和抗扰性能。这种控制策略相比于一些较复杂的控制算法来说计算量较小且较易实现，相比于与传统的PID位置伺服控制来说各项性能又都有所提升，文中的各项测试也验证了本策略的有效性和可行性。

1 电机数学模型

永磁同步电机是一个典型的非线性、多变量、强耦合系统，为了便于分析和控制，对一般的空间静止坐标系进行Clark变换和Park变换建立其同步旋转dq坐标系，并在一系列假设的基础上建立其状态空间表示的数学模型如式（1）所示。这里假设电机磁性线路中铁芯的磁饱和忽略不计；电机中的涡流损耗和磁滞损耗忽略不计；转子上无阻尼绕组，转子磁通呈正弦波分布，忽略磁场的高次谐波；定子绕组的空载电势为正弦波。

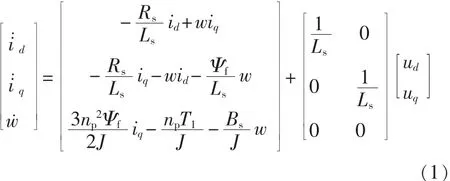
式中：id、iq——d，q轴电流；

ud、uq——d，q轴电压；

w——电机转子电角频率；

“·”——微分算子；

Rs——定子电阻；

Ls——d，q轴的等效电感；

Ψf——转子磁链；

np——转子磁极对数；

J——电机的转动惯量；

T1——负载转矩；

Bs——电机的摩擦系数。

接下来通过反馈线性化方法对式（1）进行线性化[11]，定义状态变量 x=[idiqw]T，输入量 u=[uduq]T，输出量y=[idw]T，对输出连续求导，直到式子中出现输入为止，得到的结果如下式所示：

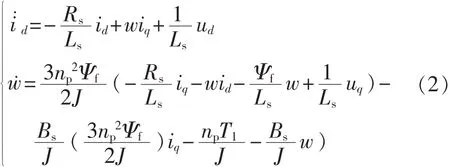
2 估计器设计

等价输入干扰（EID）估计器的主要原理是通过观测器对被控对象受到的扰动总和进行估计，再通过计算等效到输入端进行补偿，同时通过控制器调整输入量，即可通过补偿的方法抑制干扰[10]。引入干扰量d后，式（3）所示的PMSM的线性化模型可以简化写为下式所示的形式。

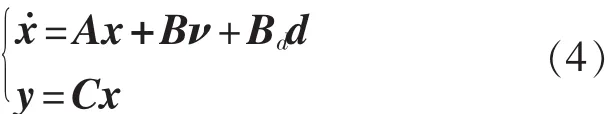
式中：x——状态变量；

ν——输入量；

y——输出量；

d——干扰量；

“·”——微分算子；

A、B、C、Bd——常系数矩阵。

将负载转矩T1视为常量并将其变化看做干扰量d的一部分。在此线性模型的基础上，构造如图1所示的带干扰估计器的伺服控制系统，包括被控对象、状态观测器、滤波器、反馈增益和控制器。

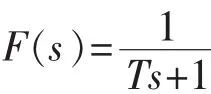
3 控制器设计

由于图1中的等价输入干扰估计器和控制器满足分离原理[12]，因而控制器可以独立设计。本文在PMSM控制系统常用的id=0矢量控制的基础上采用Backstepping方法和前馈控制方法设计了一种具有高稳定性同时又能快速响应的复合控制器。

Backstepping控制方法是一种通过逐步修正子系统控制律来实现全局渐进稳定的控制方法，将整个系统分为几个子系统，对每个子系统，通过选取合适的控制律构造Lyapunov函数来设计实现各阶的稳定性并依阶数逐步修正[14]。根据Lyapunov稳定性定理，对由状态方程描述的系统，如果存在一个李雅普诺夫标量函数W（x），满足函数本身正定且W（0）=0，其一阶导数负定，且‖x‖→∞时W→∞，则该系统具有全局渐进稳定性，故可以依此定理来构造合适的Lyapunov函数和修正各阶之间的虚拟控制量，实现整个系统的全局渐进稳定。

前馈控制一般包括速度前馈和加速度前馈，可以有效改善系统对指令的响应速度，且由于前馈不形成回路，所以不影响系统的稳定性，在信号动态跟踪方面具有良好的控制效果[9]。

综上，将两种方法相结合构造的复合控制器以实现控制系统响应速度和稳定性的均衡。根据式（3），可将本系统分解为1个一阶子系统和1个三阶子系统，分别进行 Backstepping设计。 定义 x1=id，x2=p，x3=w，x4=iq，为与w的定义相对应，定义p为电机的电角位移，可以得到如下式所示的表示：

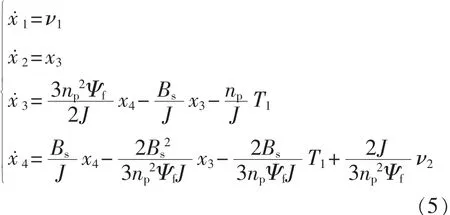
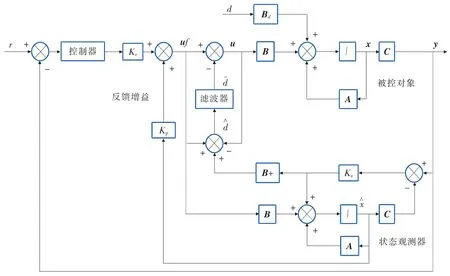
图1 带EID估计器的控制系统结构框图

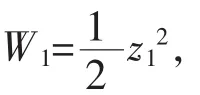
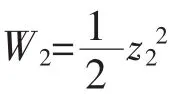
综上，可以得到控制量ν的表示和复合控制器的构造。

4 实验测试

通过Matlab软件建立该位置伺服系统的整体模型并通过计算机进行仿真实验，分别对估计器性能、系统阶跃响应、动态跟踪性能和鲁棒性进行测试，并与传统PID位置伺服控制进行对比分析。

电机模型的相关参数选取为：Rs=2.875 Ω，Ls=0.008 5 Ω，Ψf=0.175 Wb，np=4，J=0.000 8 kg·m2，Bs=0.02 N·ms；依次设置估计器和控制器的参数L、Kp、Kr、K1、K2、C1、C2、C3、C4；设负载 T1为恒值，将外部干扰以及负载变化和参数变化带来的影响均转化为干扰量d，考虑到干扰估计器的输入为二维，故将干扰量d也设置为二维，则可以取Bd=B，取如下式所示的干扰d。

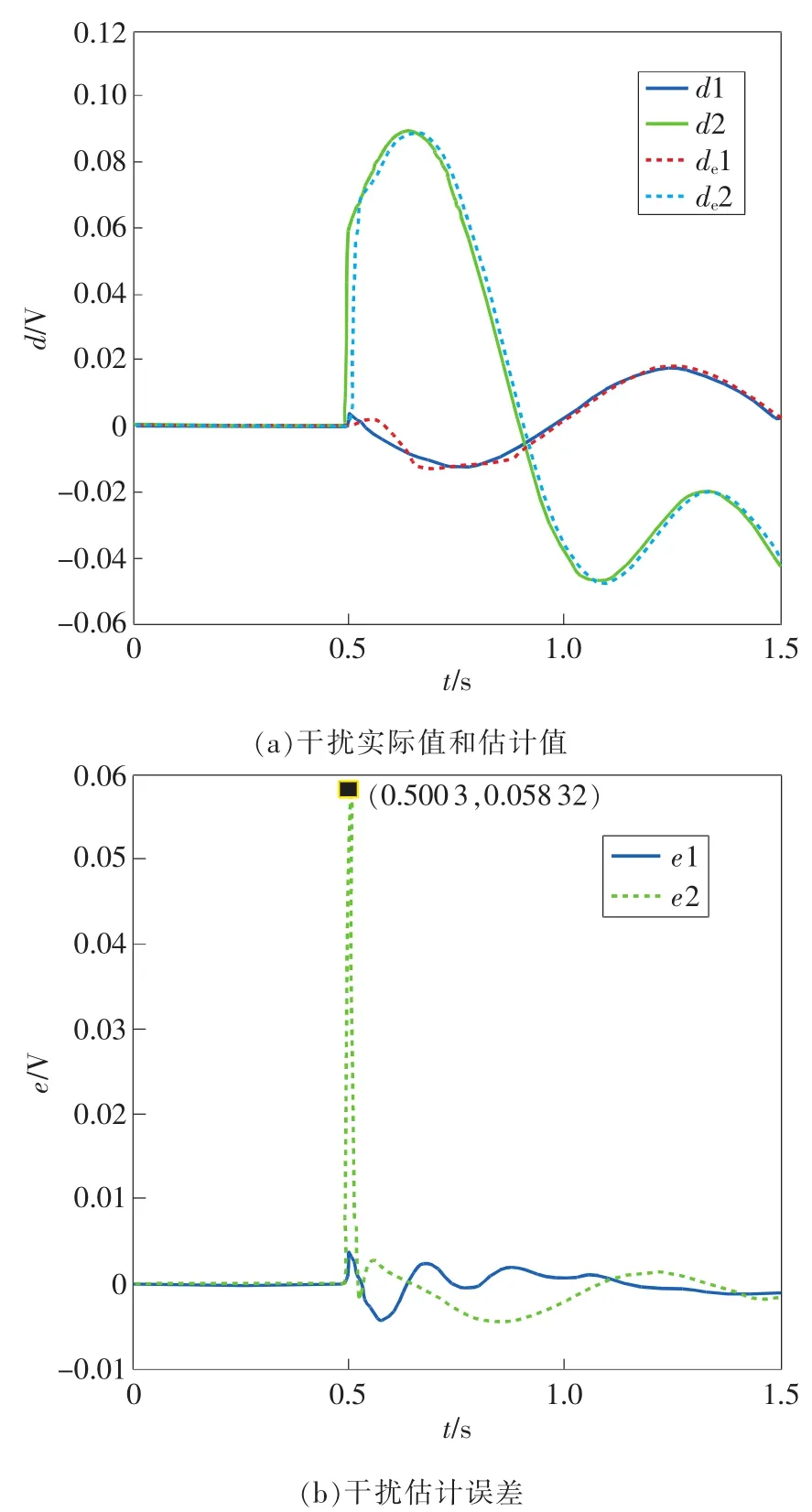
图2 干扰估计器测试结果

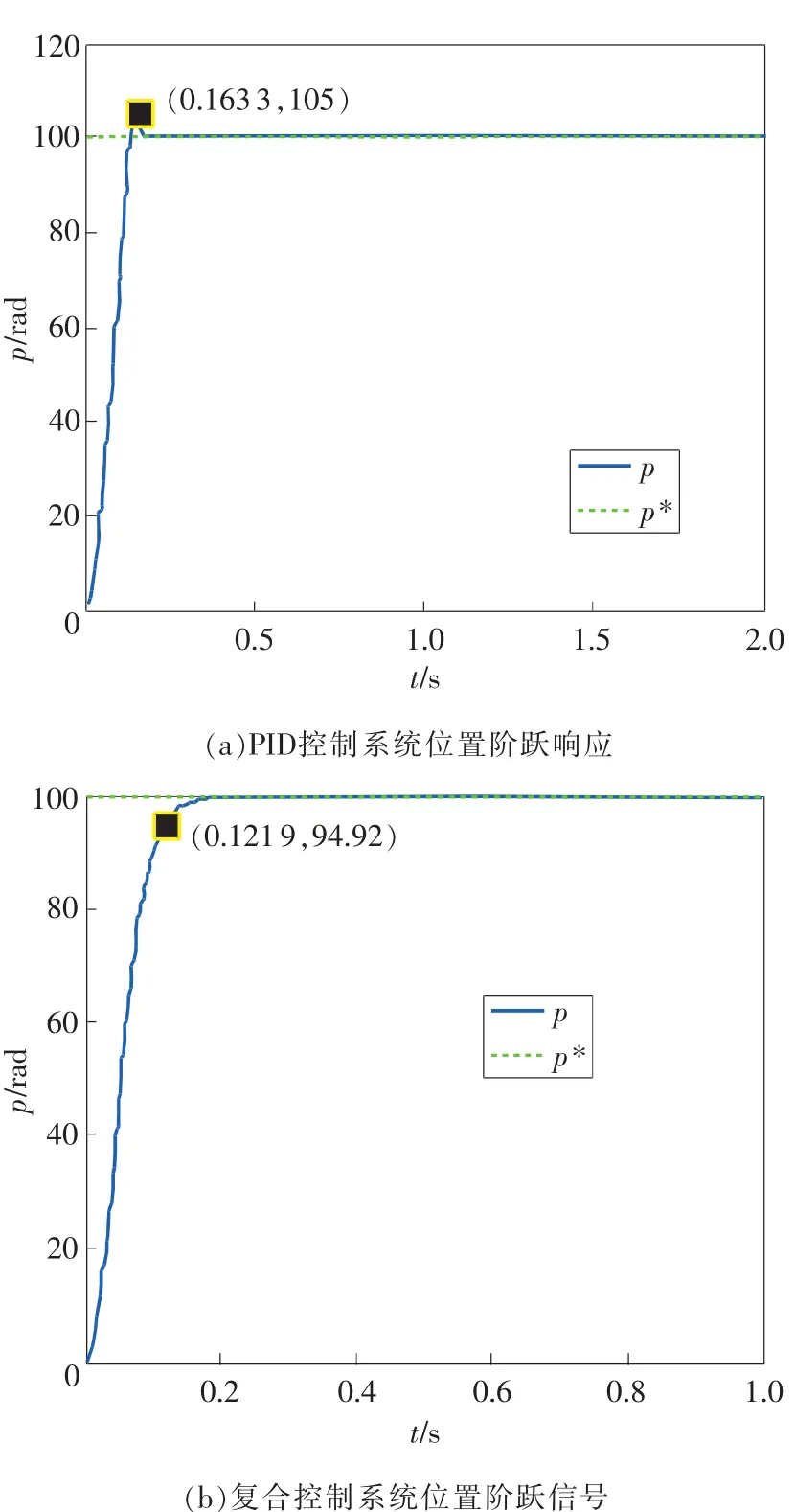
图3 阶跃测试结果

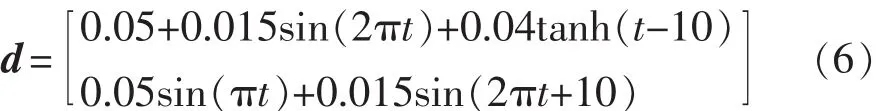
在仿真时间为0.5s处加入干扰，测试估计器的干扰估计效果，测试结果如图2所示。图中d1，d2为干扰的实际值，de1，de2为干扰的估计值，e1，e2为干扰的估计误差，在干扰突变处会有尖峰误差，其后估计值与实际值基本重合，误差保持在±0.005V以内，表明估计器可以有效估计干扰值。

在此基础上，给定位置输入指令p*=100 rad，对采用复合控制器的位置伺服系统进行阶跃测试，并与传统PID控制位置伺服系统进行对比，测试结果如图3所示。图中p*为位置指令输入信号，p为实际输出的位置信号，在PID控制系统中位置阶跃响应的超调为5.9%，调节时间为0.163 s，加入干扰后无明显波动；在复合控制系统中位置阶跃响应无超调，调节时间为0.122 s，其稳定性和响应速度较PID控制系统有明显改善，加入干扰后无明显波动。从测试结果可以看出，由于两种控制系统中均使用了干扰估计器对系统所受干扰进行补偿，所以在受到干扰时均具有较好的调节效果，再次验证了干扰估计器的可靠性；比较而言采用复合控制器的伺服控制系统具有更快更好的动态特性和稳定性。

为测试系统的动态跟踪能力，将位置指令输入信号换为幅值为1rad的低频正弦信号，去掉干扰，其他参数不变，仿真结果如图4、图5所示。图中p*为位置指令输入信号，p为实际输出的位置信号，e为跟踪误差，可以看出，复合控制系统较传统PID控制系统具有更小的跟踪误差和更好的跟随效果。

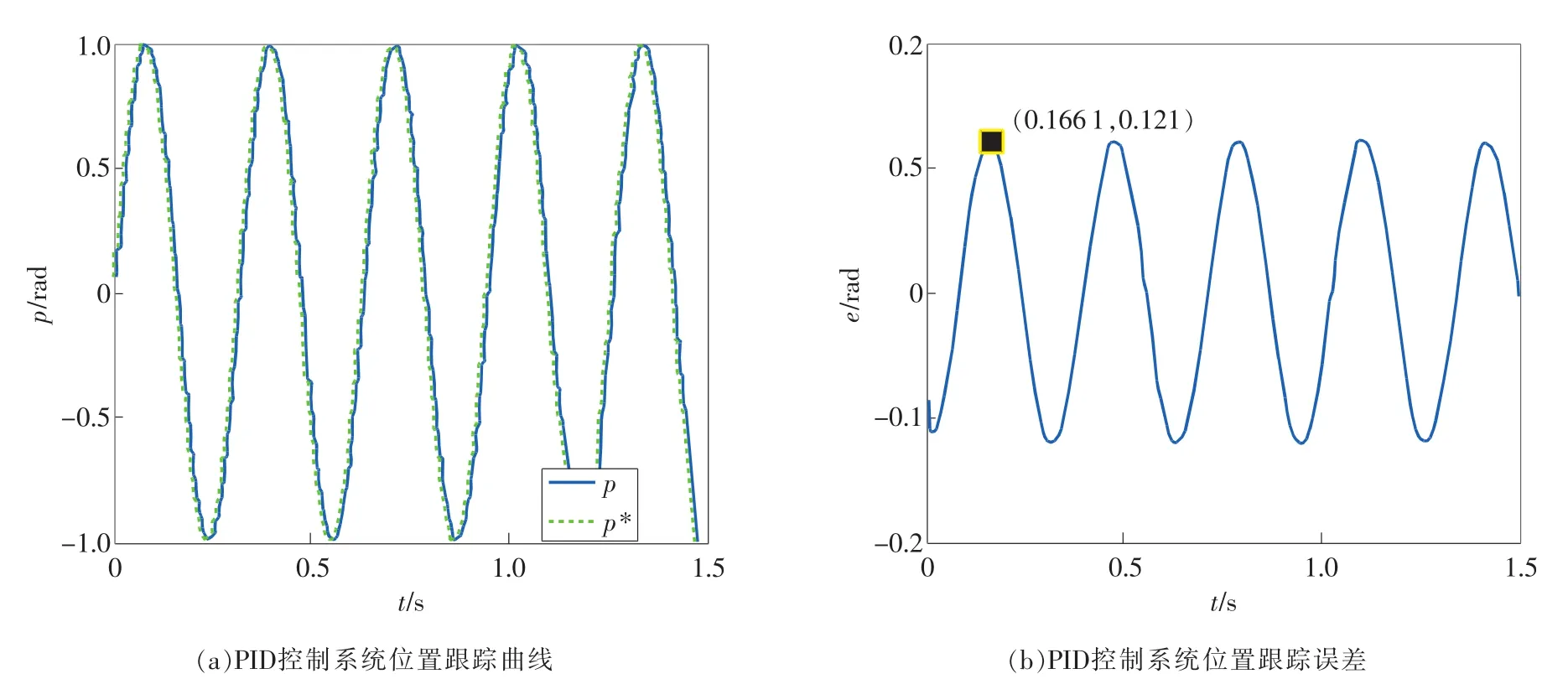
图4 PID控制系统动态跟踪测试结果

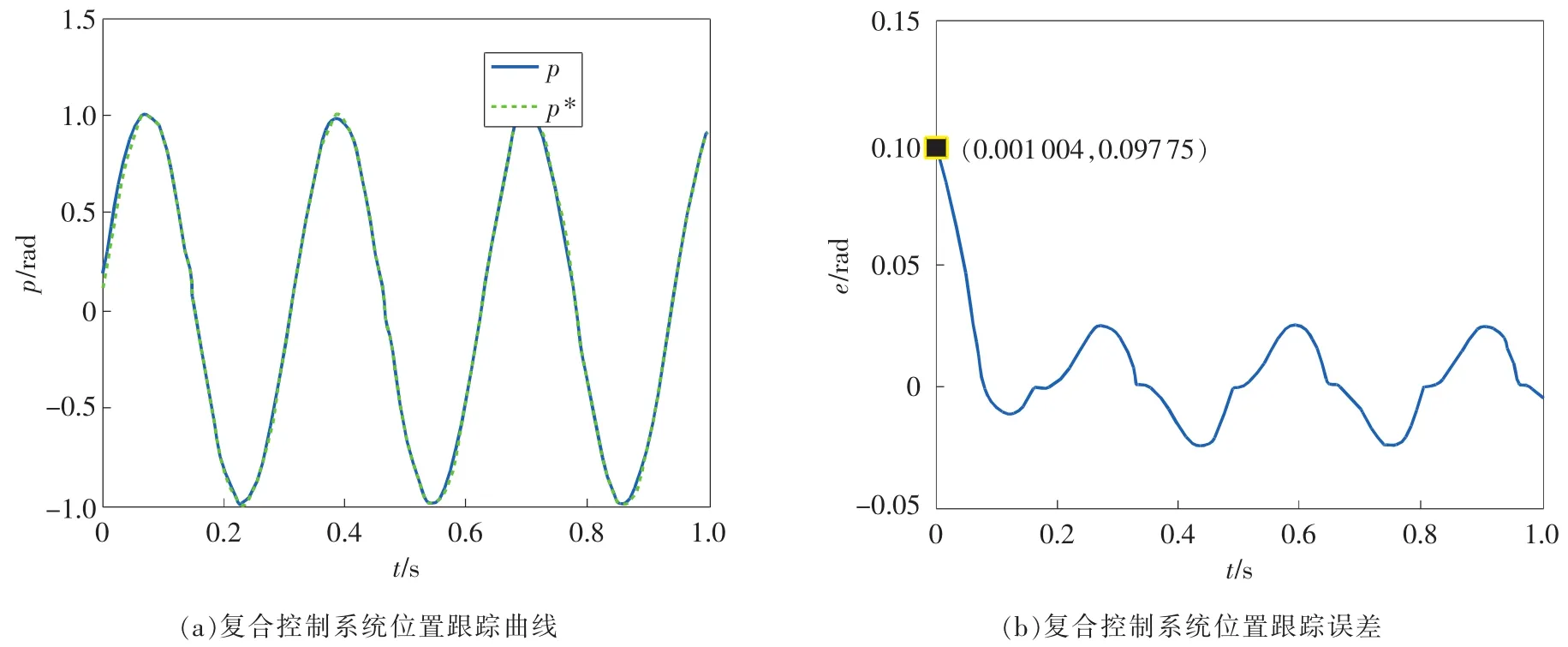
图5 复合控制系统动态跟踪测试结果

为测试系统的鲁棒性能，对电机参数进行修改，将电机转动惯量J放大100倍由0.0008kg·m2改为0.08 kg·m2，其他参数不变，位置指令输入仍为幅值为1rad的正弦信号，仿真结果如图6所示。图中p*为位置指令输入信号，p为实际输出的位置信号，与图4、图5对比可以看出，参数发生变化后，PID控制系统控制效果变差，复合控制系统仍有较高的跟踪精度，具有良好的鲁棒性。

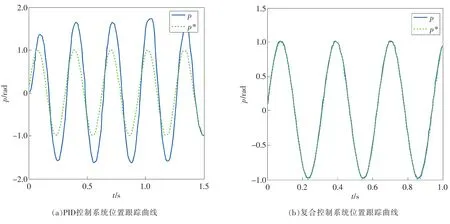
图6 鲁棒性测试结果

5 结束语

稳定性是伺服系统正常运行的基本条件，快速性是现代高性能伺服系统的基本要求，而对于受到干扰参数时变的系统来说良好的鲁棒性是又一基本要求。本文针对伺服系统的这3项基本要求，设计了永磁同步电机位置伺服系统的鲁棒抗扰控制策略，并通过仿真实验对其进行了阶跃性能测试、动态跟踪性能测试和鲁棒性测试，结果表明所设计控制系统具有良好的稳定性、动态跟踪特性和鲁棒性，但考虑到在设计控制器时用到的Backstepping算法的运算量和运算复杂程度随系统阶数的增加成倍数增长，故此控制器针对鲁棒性和稳定性要求较高但阶数不高的非线性系统更为可行。

[1]YANG J Y，ZHANG P， LIU X J.Generalized predictive control of PMSM[C]∥2013 25th Chinese Control and Decision Conference， 2013：816-820.

[2]PAWLOWSKI A， GUZMAN J L， NORMEY-RICO J E，et al.Improving feedforward disturbance compensation capabilities in generalized predictive control[J].Journal of Process Control，2012，22（3）：527-539.

[3]向红标，王收军，张春秋，等.Stribeck模型自适应滑模摩擦补偿控制[J].中国测试，2015，41（9）：92-95.

[4]YANG J， LI S H， YU X H.Sliding-mode control for systems with mismatched uncertainties via a disturbance observer[J].IEEE Transactions on Industrial Electronics，2013，60（1）：160-169.

[5]WU M，ZHOU L，SHE J H.Design of observer-based H∞robust repetitive-control system[J].IEEE Transactions on Automatic Control，2011，56（6）：1452-1457.

[6]高泽东，李建军，高教波，等.模糊自整定PID算法在伺服控制中的应用研究[J].自动化仪表，2011（10）：55-59.

[7]顾德英，吴成赛，侯娇.基于补偿模糊神经网络的BLDCM伺服控制[J].东北大学学报（自然科学版），2013（1）：13-16.

[8]张强，吴庆宪，姜长生，等.基于Backstepping的非仿射非线性系统鲁棒控制[J].控制与决策，2014（1）：19-26.

[9]郝双晖，蔡一，郑伟峰，等.基于前馈控制的交流伺服系统高速定位控制[J].微特电机，2010（2）：35-40.

[10]SHE J H，XIN X，PAN Y D.Equivalent-input-disturb ance approach—Analysis and application to disturbance rejection in dual-stage feed drive controlsystem[J].IEEE/ASME Transactions on Mechatronics，2011，16（2）：330-340.

[11]纪志成，常军.基于等价输入干扰估计器的永磁同步电机无速度传感器控制[J].仪器仪表学报，2009，30（10）：2039-2043.

[12]刘瑞娟.基于等价输入干扰补偿的几类典型系统扰动抑制设计[D].长沙：中南大学，2014.

[13]侯媛彬，嵇启春，张建军，等.现代控制理论基础[M].北京：北京大学出版社，2013：146-190.

[14]张春朋，林飞，宋文超，等.异步电机鲁棒控制器及其Backstepping 设计[J].控制与决策，2004，19（3）：267-272.

（编辑：刘杨）

Research on robust control technique of PMSM position servo system

YANG Ruifeng1，2，GUO Mingming1，2，ZHANG Peng1，2，GUO Chenxia1，2
（1.School of Instrument and Electronics，North University of China，Taiyuan 030051，China；2.Automatic Test Equipment and System Engineering Research Center of Shanxi Province，Taiyuan 030051，China）

A robustdisturbance rejection controlstrategy based on backstepping control，feedforward control and equivalent input disturbance（EID） estimation is designed to improve the robustness and the disturbance suppression performance of the permanent magnet synchronous motor（PMSM） position servo system.The combination and proper parameters of backstepping control，which is a control method based on system stability， and feedforward control， which improves system response speed，can provide the system with a certain quick response ability when it is stable;the interaction with EID estimator possessing excellent disturbance rejection functions can efficiently promote the real-time tracking and anti-interference properties of the system.The estimatorisvalidated by good resultsofperformance testunderdisturbance via computer simulation experiment;while the robust control strategy is proven to be valid by step response，dynamic tracking and robust performance tests to system via simulation experiment，and through comparison and analysis of traditional PID position servo system.

position servo system；robust control；Backstepping control；equivalent input disturbance（EID）estimation；permanent magnet synchronous motor（PMSM）

A

1674-5124（2017）04-0089-06

10.11857/j.issn.1674-5124.2017.04.019

2016-11-05；

2016-12-17

国家国际科技合作专项项目（2014DFR70650）；山西省科技攻关项目（2015031007-1）

杨瑞峰（1969-），男，山西忻州市人，教授，博士，主要从事自动化测试与控制技术研究等方面的教学与科研工作。