基于copula相关性的多元质量控制研究
2017-07-18王俊棋袁龙
王俊棋,袁龙
(合肥工业大学 机械工程学院,安徽 合肥 230009)
基于copula相关性的多元质量控制研究
王俊棋,袁龙
(合肥工业大学 机械工程学院,安徽 合肥 230009)
在实际生产过程中各质量点之间存在非线性、复杂、耦合相关性,传统的SPC控制图并不能系统、全面地进行质量控制。本文构建了基于copula函数的相关性模型的多元质量控制技术,并进行实例验证。
copula;相关性;多元质量控制
1924年休哈特博士提出了控制图,这是一种在生产过程中被广泛运用的质量管理手段。然而,在实际生产中产品的质量并非是多个质量点的简单累加,往往不同质量点之间存在相互影响、相互作用。所以,考虑质量点之间相关性的质量控制图对产品质量管理具有实际意义。采用简单的线性相关模型并无法精确的描述出质量点之间的相关关系。而Copula理论在分析相关性中能够将各类相关性度量指标进行“归一”处理,可以很好地用于描述多个质量点之间的相关关系。本文提出了一种基于copula相关性的多元质量控制图,采用copula函数构建多个质量点相关性模型。对于存在较强相关性的质量点,在采用公差法进行数据标准化后采用SPC控制图进行质量控制。
1 Copula函数相关性建模
1.1 copula函数的定义
1.2 copula相关性建模
根据copula函数理论,构建基于copula函数的相关性模型的步骤如下。第一,随机变量分布的确定。当质量点服从的分布已知,使用参数法获得质量点的边缘分布函数。当质量点服从的分布未知,采用非参数估计法得到质量点的边缘分布函数。第二,选择最优的函数类型。通过质量点的历史数据分析质量点之间的相关性特点,根据其相关性特点选择合适的函数。第三,对函数中的参数进行估计。第四,通过函数模型参数描述其相关关系。采用秩相关系数以及尾部相关系数进行模型相关性评价。
以发动机缸盖线的凸轮轴的某直径和同轴度质量点为例,采用copula函数相关性模型建模分析其之间的相关性。选取1000台发动机缸盖的凸轮轴的直径以及同轴度数据,数据见表1。

表1 质量数据表
(1)采用非参数化方法确定直径与同轴度各自的边缘分布,并通过核分布函数与经验分布函数重合程度评价估计的准确性。
(2)在得到质量点的边缘分布函数,绘出二维频率直方图,见图1。
从二元频数直方图发现,直径与同轴度存在尾部相关性较强的特征。根据多种copula函数存在的特点,最合适的函数是t-copula函数。

图1 二元频数直方图
(3)函数类型得到确定以后,对函数的参数进行估计,得到函数表达式,并根据实际质量数据绘出相应的copula函数密度函数图以及分布函数图。采用matlab计算t-Copula函数参数

得到t-Copula分布函数、密度函数表达式,根据密度函数、分布函数公式绘出t-Copula密度函数图、分布函数图,见图2、3。

图2 二元t-Copula密度函数图

图3 二元t-Copula分布函数图
(4)t-Copula函数的Kendall秩相关系数:

选择t-Copula函数进行相关性分析。t-Copula函数的秩相关系数=0.7451,根据秩相关系数的定义得出结论:在使用建模的质量数据中,直径与同轴度有74.5%的数据存在波动一致性。t-Copula函数的95%分位数的尾部相关系数为0.634,即当随机变量直径取值在0.95分位数时,另一随机变量同轴度以63.4%的概率也在0.95分位数以上。
综上分析,二者存在着较强的相关性。
2 基于相关分析的质量控制图
在质量点之间存在较强相关性的基础上,对多个质量点的数据进行标准化处理以实现数据整合,实现多元到一元的质量数据处理,再进行一元统计过程控制,实现多元质量控制。
质量点的数据采用公差法进行处理,基于公差实现标准化。相对公差法转化公式如下 :
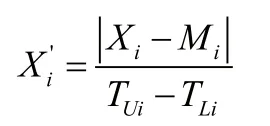
在上文的分析中,发动机缸盖的凸轮轴的直径和同轴度存在强相关性,以此为例子,构建基于copula相关性的多元质量控制图。
凸轮轴直径的目标值为25.01,上限为25.0235,下限为25.0005;凸轮轴同轴度的目标值为0,上限为0.05,下限为0。对直径的一个质量数据X1=25.0189和同轴度一个质量数据Y1=0.031使用公差法进行标准化处理,对变量进行控制图分析。

选取30对直径和同轴度质量数据,采用公差法进行标准化后,对得到的变量Z采用控制图进行质量控制,绘制单值控制图,见图4。

图4 单值控制图
3 结语
本文构建基于Copula相关性模型的多元质量控制技术,并使用发动机缸盖线的质量点进行实例验证。相比于传统的SPC控制图,考虑了质量点之间的相关性,可以在生产过程中进行更为系统、全面的质量控制。
[1]李明旻. HT公司质量管理体系的优化研究[D]. 中国地质大学(北京), 2013.
[2]李朝荣. Copula驱动的小波域纹理特征提取 研究[D]. 电子科技大学, 2013.
[3]Sklar A. Random variabl es, joint distribution functions, and copulas[J]. Kybernetika, 1973, 9(6): (449)-460.
[4]张英芝, 郑锐, 申桂香,等. 基于Copul a理论的数控装备故障相关性[J]. 吉林大学学报(工), 2011, 41(6):1636-1640.
[5]王小巧. 复杂机械产品装配过程质景自适应控制方 法及支持系统研究[D].合肥工业大学,2015.
[6]牛君. 基于非参数密度估计点样本分析建模的应用 研究[D]. 山东大学, 2007.
[7]贾庆旭. 发动机冷试与加工数据的多元相关性研究 与应用[D].上海交通大学, 2012.
[8]张根保, 冉琰. 基于模糊物元的小批量生产典型 工序能力分析[J]. 机械工程学报, 2015, 51(23):116-122.
TB497
A
1671-0711(2017)07(上)-0216-02
