基于LINGO的多智能配送单元任务分配策略研究
2017-07-18党少杰张迪
党少杰,张迪
(合肥工业大学机械工程学院,安徽 合肥 230009)
基于LINGO的多智能配送单元任务分配策略研究
党少杰,张迪
(合肥工业大学机械工程学院,安徽 合肥 230009)
为了解决作业车间任务分配缺乏合理规划等问题,本文以路径最短为目标建立了任务分配模型,然后利用LINGO软件对模型进行求解。实例结果表明,利用LINGO软件可以快速、准确的给出分配方案,从而为解决任务分配问题提供了一个有效的解决办法。
任务分配;整数规划;LINGO
1 问题提出
随着制造业市场的竞争越来越激烈,企业都在考虑如何提高生产效率,降低成本。而任务分配是企业以前很少关注的一个问题,并且该环节处理的好坏将直接影响智能配送单元对物料需求的响应速度以及物料的配送成本。一个合理的任务分配方案可以减少运送次数以及运送成本,这些指标对于企业提高生产效率节约成本起着重要作用。所以对作业车间智能配送单元的任务分配策略的研究有着非常重要的理论价值和实际意义。
对于作业车间配送单元的任务分配策略问题,目前已经有不少的文章进行了研究。传统的平衡指派问题(AP,Assignment Problem)采用匈牙利算法进行求解,在匈牙利算法的基础上,提出了一种任务指派问题的快速求解方法-剪枝优化算法,该算法大大提高了求解任务指派问题的求解速度。文献提出一类带时间约束的指派问题,即每台机器有执行任务的时间窗限制,并给出分枝定界算法。文献采用lingo软件求解了钢铁企业产成品转库运作中的混合车辆指派及路径优化问题。目前对基于时间窗和容量双约束的研究不足,本文的模型基于时间窗和容量双约束建立。
随着计算机技术的大战,已经有十分强大的软件用于解决运筹学问题,其中对规划问题的求解最好的软件就是LINGO软件,目前LINGO软件已经升级到12.0版本,本文就是通过LINGO软件来对模型求解,实例结果表明其可以迅速给出一套经济、可行的任务分配方案。
2 模型建立
作业车间任务分配策略是合理规划、指派智能配送单元以便于将物料可以及时、准确地运送到需求工位,由于作业车间多智能配送单元的任务分配策略问题比较复杂,因此在建模的过程中必须考虑智能配送单元任务分配原则、物料需求情况、配送单元的最大容量、作业车间的布局等因素,如果智能配送单元物料配送策略不合理,可能使物料配送时间过长,导致生产成本增加,鉴于作业车间中物料配送多智能配送单元任务分配策略研究的复杂性,故作如下假设:(1)生产节拍、作业车间布局、智能配送单元数量和容载量已知。(2)所有需求工位只需配送一次,一个智能配送单元一次最多只能去一个工位。(3)假定所有智能配送单元同一型号(容载量、速度等)。(4)智能配送单元的容载量要大于需求工位的需求量。
建立的数学模型如下:

其中式(1)为目标函数;式(3)代表每个需求工位只能由一个智能配送单元的某个任务去配送;式(4)代表某个智能配送的指定任务最多只能去一个需求工位;式(5)表示智能配送单元完成所有的物料配送任务;式(6)是时间窗约束;式(7)是容量约束;式(8)示每台智能配送单元任务的总数小于总的物料配送任务。
3 实例验证
某工厂6个小车,8个需求工位距离二位表和工位时间表如图1所示。

表1 小车—工位距离表

表2 小车—工位时间表
下面是针对模型写的编写的lingo程序。
model:
sets:
car/car1..car6/: limit_assitant,capacity;
number/number1..number3/:num;
station/station1..station8/: request,time_start,time_ end;
links(car,number,station):distance, time_between, vo;
endsets
!目标函数;
min=@sum(links : distance*time_between* vo);
!一个车一次最多只能去1个工位(一次可以去多个工位);
@for(car(I):
@for(number(J):
@sum(station(K): vo(I,J,K))<=1));
!一个工位只能由一个车去响应;
@for(station(K):
@sum(number(J):
@sum(car(I): vo(I,J,K)))=1);
!容量约束加变量;
@for(car(I):
@for(number(J):
@sum(station(K):vo(I,J,K)*request(K))<= capacity(I)));
!任务数约束;
@for(car(I):
@sum(number(J):
sum(station(K):vo(I,J,K)))<= imit_assitant(I));
!整数约束;
@for(links: @bin(vo));
!总和约束;
@sum(car(I):
@sum(number(J):
@sum(station(K):vo(I,J,K))))=8;
!时间窗约束;
@for(station(K):
@for(number(J):
@sum(car(I):time_between(I,J,K)*vo(I,J,K)) <=time_end(K)-time_start(K)));
在LINGO12.0上运行程序返回如下结果(图1~2)
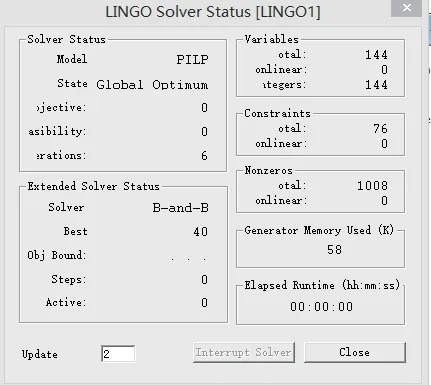
图1 LINGO求解状态

图2 LINGO求解结果
因此,任务分配方案是:1号车配送工位5和2;2号车配送工位7;3号车配送工位3;4号车配送工位8;5号车配送工位1;6号车配送工位6;6号车配送工位4。
4 结语
本文对作业车间的任务分配问题进行分析,建立了数学模型,并且采用LINGO软件进行了求解。实验证明采用LINGO软件可以高效、便捷地求解此类问提。当然一些启发式算法、智能算法也可以求解此问题,值得另行研究。
[1]邹莉. 多目标电梯群控系统的研究[J]. 自动化与仪器仪表, 2010(3):14-16.
[2]马云红, 井哲, 周德云. 一种任务分配问题的快速剪枝优化算法[J]. 西北工业大学学报, 2013, 31(1):40-43.
TH165
A
1671-0711(2017)07(上)-0206-03
