首发浮动的高初速榴弹机枪发射性能研究

宋 杰,邱 明,廖振强,华洪良

(南京理工大学 机械工程学院,江苏 南京 210094)

首发浮动的高初速榴弹机枪发射性能研究

宋 杰,邱 明,廖振强,华洪良

(南京理工大学 机械工程学院,江苏 南京 210094)

为研究采用首发浮动技术的榴弹机枪(GMG)的动力学特性,建立GMG刚柔耦合动力学模型,并进行了20连发动力学计算。通过动力响应研究了浮动参数对射击密集度的影响。采用外弹道理论计算了20连发射击密集度,并与实验值进行比较,对动力学模型的准确性进行了验证。研究了浮动参数对武器架座力及射击密集度的影响规律。研究结果表明:建立的仿真计算模型可以有效预测GMG射弹散布,并可通过合理匹配浮动参数达到提高武器射击密集度、降低武器后坐力的目的。

榴弹机枪;高初速;浮动参数;射击密集度;仿真

榴弹机枪(GMG)在射击过程中枪管与机框作为浮动体沿枪管轴线方向高速往复运动,造成枪身质心位置在射击循环中是变化的,枪架及枪管的动态特性相应产生变化,这是浮动发射方式的特点[1]。相对于普通发射方式,浮动发射可以大幅降低武器后坐力[2]。国内外学者对采用首发浮动的武器减后坐方面做了大量研究[3-7],而对武器的射击密集度研究仍然很少。研究浮动方式自动机动力学特性、分析膛口响应特性是研究武器射弹散布变化规律的前提。弹丸起始扰动是造成射弹散布的根本原因,包括弹丸速度、射角和弹道系数[8]。本文重点研究弹丸出膛口时速度对射弹散布及射击密集度的影响。膛口振动特性决定弹丸出膛口速度,正确计算枪管膛口运动特征量是研究武器射弹散布及射击密集度的关键。柔性架座是搭载枪身的射击平台,架座的振动直接影响枪身的振动[9],枪管及架座的变形对系统的振动特性不可忽略,枪管和架座不能按照刚体处理,必须考虑柔性效应。

本文利用动力学分析软件对首发浮动的高初速GMG进行动力学建模,计算膛口振动特性曲线。将弹丸出膛口初始扰动量作为外弹道方程初始条件,计算武器射击密集度。通过对比射弹散布仿真值与试验值,验证了所建模型的正确性。

1 首发浮动GMG工作原理

首发浮动GMG示意图如图1所示,工作原理:机框在机框复进簧作用下带动枪机完成复进、推弹入膛、闭锁动作。在机框闭锁后走自由行程时,机框的楔形面撞击枪管锁扣,完成对枪管解锁动作,随后机框组件与枪管在机框防跳器作用下扣合在一起共同复进。当机框组件与枪管组件运动至最大前冲位置时击发底火。弹底压力大于弹丸挤进压力时,榴弹在火药燃气压力作用下挤进膛线加速运动。榴弹运动至导气孔之前,枪管、机框组件呈闭锁状态一起后坐。当榴弹经过导气孔时,部分火药燃气由导气孔流入导气室,一方面推动活塞加速运动,活塞解脱机框防跳器,另一方面迫使枪管减速。活塞推动机框加速运动,完成开锁动作。枪机与机框一起后坐,在拉壳钩作用下完成抽壳、抛壳。机框后坐过程中带动拨弹滑板进行拨弹、脱链动作。枪机与机框后坐撞击机框缓冲器直至后坐到位,而后开始复进完成下一发自动循环动作。同时,枪管在枪管浮动簧力、膛内压力作用下后坐、后坐到位、复进,直至枪管被枪管锁扣卡在枪管首发初始位置处,等待机框解锁。

2 刚柔耦合建模

为了减少计算工作量,将刚度大、变形小且对射击系统发射动力学影响不大的部件当作刚体进行研究。对自动机运动及受力影响不大的零部件进行等效质量和转动惯量替代。对刚度小、变形大且对武器射击密集度影响大的零部件按柔性体进行建模。结合图1所示首发浮动GMG低后坐发射系统,利用有限元软件将枪管组件、上架、托架和三脚架生成柔性体,其余零部件作相应的刚体、等效质量处理,得出基于高初速发射的GMG刚柔耦合动力学计算模型。

2.1 载荷添加及边界处理

2.1.1 膛压曲线及导气室压力曲线

膛内和导气室气体压力是导气与枪管混合式武器的动力来源,准确计算膛内和导气室的气体压力参数是建立武器动力学模型的基础,直接影响武器仿真结果的正确性和合理性,在武器动力学分析中具有重要地位。关于气体动力学计算模型,文献[1]中已作详细推导,这里不再赘述,通过气体动力学模型得到武器膛压曲线和导气室压力曲线,如图2所示。

2.1.2 土壤集总参数模型

架座与土壤介质之间相互作用,对GMG的动力学特性有很大影响。建立土壤模型时,选取广泛采用Nemak和Rosenblueth提出的集总参数模型[10]。土壤集总参数计算公式为

(1)

式中:mh,mv分别为水平方向和高低方向的等效质量;Kh,Kv分别为土壤对驻锄作用力在水平和高低方向上的等效刚度;Ch,Cv分别为土壤对驻锄作用力在水平和高低方向上的等效阻尼系数;r为与土壤有效接触面积的当量半径;ρs为土壤质量密度;G为土壤剪切弹性模量。

2.2 射击密集度计算模型

外弹道模型为

(2)

式中:C为弹道系数;H(y)为空气密度函数;FR(v)为与弹丸飞行有关的阻力函数;s为弹丸飞行距离。

外弹道初速条件为

式中:v0为弹丸出膛口速度;Δθx0,Δθy0分别为弹丸出膛口瞬间方向射角、高低射角的初始扰动量;Δvx0,Δvy0为弹丸出膛口瞬间在x轴、y轴方向上速度的初始扰动量;δx0,δy0为弹丸出膛口瞬间在x轴、y轴方向上的位移初始扰动量。根据弹丸在膛口的初始扰动量,将弹丸后效期结束时刻的参量代入外弹道方程组,求解得到射击距离100m的射弹散布。

用密位(mil)单位表示的立靶密集度为

(3)

3 仿真分析计算及模型验证

3.1 自动机动力学特性分析

对上节建立的高初速GMG模型进行20发射击仿真计算,得到连发射击自动机动力学特性曲线,如图3所示。

由图3(a)可知,机框复进行程为405 mm,缓冲行程为20 mm,枪管前冲行程为100 mm,后坐行程为120 mm,完成20发的射击时间为3.861 1 s,射速为311 r/min。

由图3(b)可以看出,机框在首发达到最大后坐速度为7.65 m/s,这是由于首发时机框由静止开始加速运动,而第2发开始,机框在撞击机框缓冲簧时有反跳速度,反跳速度抵消一部分后坐冲量,枪管首发出现最大后坐速度亦是如此;机框在第3发达到最大前冲速度5.22 m/s。图4为机框和枪管的速度峰值随弹序(Nd)的变化趋势图。由图4可知,机框最大前冲速度自第5发后交替出现衰减,呈现收敛趋势,可以认为武器射击过程趋于稳定。枪管在首发射击时达到最大后坐速度6.06 m/s,在第3发射击时出现最大前冲速度5.22 m/s。

为了更确切地描述武器摇架的受力状况,双向缓冲簧力定义为架座力;将沿枪管后坐方向所受缓冲簧力定义为后坐力,图3(c)中以负值表示;沿枪管前冲方向所受缓冲簧力定义为前冲力,图3(c)中以正值表示。低后坐发射是指武器在射击过程中前冲力峰值、后坐力峰值均较小。由图3(c)可以看出,武器在第2发击发时达到最大后坐力,在第2发机框与枪管撞击结合时达到最大前冲力。

3.2 射击密集度分析

通过2.2节外弹道计算模型可知,弹丸初始扰动量是造成射弹散布的主要原因,包括δy0,δx0,Δθy0,Δθx0,Δvy0,Δvx06个参数。通过对建立的高初速GMG刚柔耦合模型进行20发射击仿真计算,得到膛口位置处6个参数值,具体参数值见表1。

表1 膛口初始参数

通过在ADAMS中设立传感器,截取弹丸出膛口时刻,通过Matlab软件编程提取弹丸出膛口瞬间20组膛口6个初始扰动量,将提取的位移初始扰动量、速度初始扰动量、射角初始扰动量作为外弹道计算初始条件,计算在100 m距离上射弹的弹着点。图5为100 m距离上射弹散布仿真结果和试验结果。表2为射弹散步圆及射击密集度仿真值、试验值,相对误差在10%内。表中,R50是以散布中心为圆心,包含弹着点数50%的圆半径;R100是以散布中心为圆心,包含弹着点数100%的圆半径。可以看出武器仿真结果与试验结果基本相符,提取的刚柔耦合模型中膛口初始参数数据是可靠的,建立的射击密集度模型是正确的。

表2 射击密集度

由表2可知,GMG高低方向射击密集度试验值是方位方向射击密集度试验值的1.7倍,GMG高低方向散布较大。将图5射弹散布仿真结果进行射弹排序,R50试验值只有R100试验值的16%,主要由于GMG在前3发射击时未达到稳定射击状态,前3发离散较严重,但第3发后散布逐渐变小,呈现向散布中心收敛的状态。

4 浮动装置结构参数对架座力及射击密集度的影响

合理采用浮动装置有3个优点:①能够大幅减小后坐力,在复进中浮动体的能量抵消火药燃气后坐能量;②大幅降低运动件之间的撞击力,减小武器的振动;③在射击高速榴弹时浮动簧对机匣作用力始终向后,提高武器射击稳定性及射击密集度。结合研究的首发浮动GMG特点,下文研究浮动行程、浮动簧刚度、浮动解锁位置对GMG发射性能的影响,对降低武器后坐力、提高射击密集度具有重要意义。

4.1 浮动行程

图6为架座在20连发射击过程中所受前冲力和后坐力的峰值。图中,Fmax为负值表示后坐力峰值,Fmax为正值表示前冲力峰值。浮动行程Lf在105～85 mm范围内架座力逐渐衰减或者小幅震荡,保证浮动的稳定性。由图6可以看出:武器在前3发未达到射击稳定状态,出现架座力峰值波动较大的现象,且在20连发射击过程中最大后坐力出现在前3发阶段;当Lf=105 mm时后坐力最大,而当Lf=95 mm时后坐力最小;第5发弹后架座力峰值开始趋于稳定;第20发浮动自动机达到最稳定状态,随着浮动行程变短架座所受前冲力峰值逐渐增大,且Lf=85 mm比Lf=105 mm的前冲力峰值大72.8%,Lf=85 mm后坐力峰值最大,Lf=90 mm后坐力峰值最小,且Lf=85 mm比Lf=95 mm后坐力峰值大54.6%。一方面前冲力及后坐力尽量小,另一方面架座力最大值与达到稳定浮动后峰值波动尽量小,架座力控制在3 500 N内浮动行程取85～100 mm范围内合适。

图7为浮动行程对100 m立靶上射弹散布的影响,表3为浮动行程对射击密集度的影响。结合表3可知:缩短浮动行程,散布中心在方位方向逐渐沿X轴正方向偏移,且浮动行程Lf≤95 mm时弹序大的榴弹弹着点开始向靶纸右上方向发散;R50在浮动行程Lf=95 mm时最小,在Lf=85mm时最大;R100在浮动行程Lf=100 mm时最小,在Lf=85 mm时最大;当Lf=95 mm时高低方向射击密集度Eyy和方位方向射击密集度Exx最小,当Lf=85 mm时高低方向射击密集度Eyy和方位方向射击密集度Exx最大。从射击密集度考虑,浮动行程在95～105 mm范围内合适。

表3 浮动行程对射击密集度的影响

综上所述,GMG浮动行程在95～100 mm范围内较合理,既能将架座力控制在3 500 N范围内达到武器低后坐发射的目的,又能满足高低方向射击密集度Eyy≤1.6,方位方向射击密集度Exx≤1,实现武器高精度的指标。

4.2 浮动簧刚度

图8为不同浮动簧刚度下架座力峰值随弹序的变化图。由图8可知:武器在20发射击过程中最大前冲力、最大后坐力出现在前两发的射击过程中;浮动簧刚度Kf=5.5 N/mm时前冲力(2 549 N)最大,Kf=3.5 N/mm时后坐力(3 378 N)最大;第3发之后前冲力峰值、后坐力峰值开始趋于稳定;第20发射击时浮动状态最稳定,随着浮动簧刚度增大,前冲力峰值增大,且Kf=5.5 N/mm比Kf=3.5 N/mm前冲力峰值大109.8%,Kf=5.5 N/mm时后坐力峰值最大,Kf=4.5 N/mm时后坐力峰值最小,且Kf=5.5 N/mm比Kf=4.5 N/mm时后坐力峰值大36.1%。武器架座力控制在3 500 N内,浮动簧刚度取在3.5～5.5 N/mm范围内较合适。

图9为浮动簧刚度对100 m立靶上射弹散布的影响,浮动簧刚度对射击密集度的影响如表4所示。结合表4可知:增大浮动簧刚度,散布中心在高低方向上沿Y轴正方向逐渐偏移,在方位方向上沿X轴正方向逐渐偏移;当浮动簧刚度Kf≥5.0 N/mm时,弹序大的弹着点开始沿靶纸右上方向发散;R50在Kf=5.0 N/mm时最小,在浮动簧刚度Kf=4.0 N/mm时最大;射弹全散布R100随浮动簧刚度增大而增大;当Kf=4.0 N/mm时Eyy最小,当Kf=4.5 N/mm时Exx最小;当Kf=5.5 N/mm时Eyy和Exx最大。从射击密集度考虑,浮动簧刚度在3.5～5.0 N/mm范围内合适。

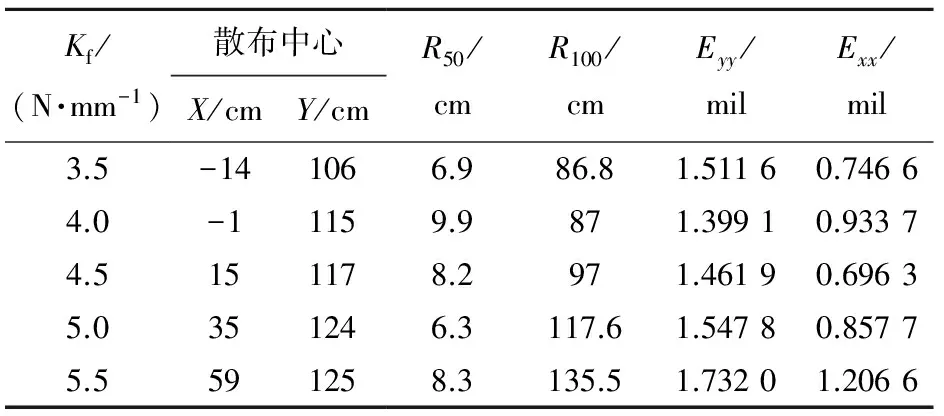
表4 浮动簧刚度对射击密集度的影响

综上所述,首发浮动的GMG浮动簧刚度取值在3.5～5.0 N/mm范围内较合理,既能将架座力控制在3 500 N内实现武器低后坐发射目的,也能满足Eyy≤1.6且Exx≤1,达到武器高精度的指标。

4.3 浮动解锁位置

浮动解锁位置决定枪管解脱时间,文中解锁位置取值越大表示越靠近膛口。当枪管提前被解锁,浮动簧对枪管作用力使枪管获得较大加速度,机框在机框复进簧作用下加速度较小,可能会出现下列2种情况:机框与枪管未扣合在一起,最终机框与枪管分离无法进行击发;机框与枪管前冲至最前端,枪管撞击瞎火缓冲装置,而此时枪管速度无前冲速度,机框前冲至击发位置击发底火,武器相当于枪管长后坐自动方式,后坐力急剧增大。当枪管解锁位置越小,机框走完自由行程与枪管碰撞结合速度损失越多,浮动前冲至最大位移处速度越低,浮动机动能抵消火药燃气能量越少。因此,合理选择浮动解锁位置不仅能够降低GMG后坐力、提高射击精度,而且可以有效避免瞎火现象。

图10为不同浮动解锁位置下架座力峰值随弹序的变化图。由图10可知:武器在20发射击过程中最大前冲力、最大后坐力出现在前两发的射击过程中;浮动解锁位置df=5 mm时前冲力(2 103 N)最大,df=20 mm时后坐力(3 601 N)最大;第3发之后df=20 mm浮动状态不稳定,前冲力峰值、后坐力峰值大幅振荡,其余浮动解锁位置小幅振荡且随着射击发数增加而逐渐收敛;第20发射击时浮动状态相对稳定,df=20 mm时前冲力峰值最大,df=5 mm时前冲力峰值最小,且df=20 mm时比df=5 mm时前冲力峰值大88.1%,df=20 mm后坐力峰值最大,df=5 mm时后坐力峰值最小,且df=20 mm时比df=5 mm时后坐力峰值大59.8%。为实现武器低后坐发射浮动解锁位置取在0～15 mm范围内较合适,其中以df=5 mm方案最优。

图11为浮动解锁位置对100m立靶上射弹散布的影响,浮动解锁位置对射击密集度的影响如表5所示。结合表5可知:浮动解锁位置在5～15 mm范围内散布中心大致相同,在高低方向及方位方向上df=20 mm时偏移量最大,当df≥15 mm时弹序大的弹着点开始沿靶纸右上方向发散;R50在df=5 mm时最小,在df=20 mm时最大;浮动解锁位置在0～15 mm范围内射弹全散布R100大致相同,在df=20 mm时最大;在df=10 mm时Eyy和Exx均最小;在df=20 mm时Eyy和Exx均最大。从射击密集度考虑,浮动解锁位置在0～15 mm范围内合适。

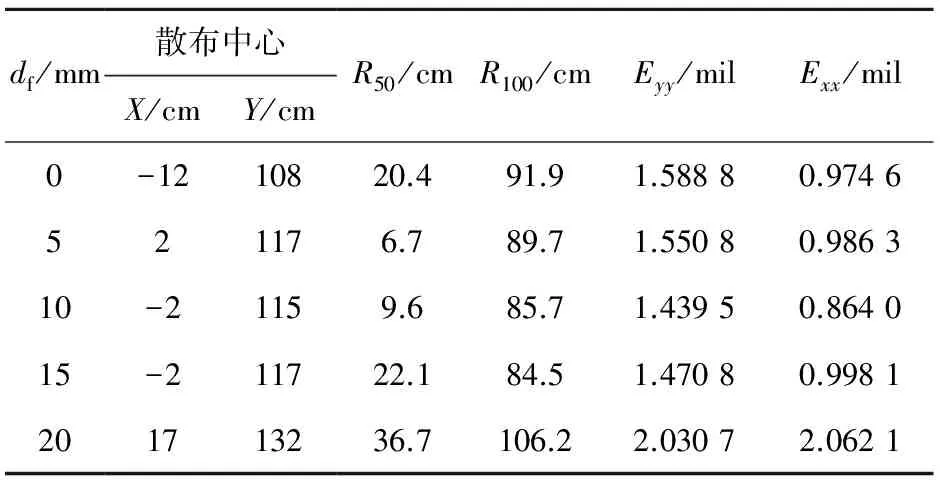
表5 浮动解锁位置对射击密集度的影响

综上所述,浮动解锁位置取值在0～15 mm范围内较合理,既能将武器架座力控制在3 500 N范围内实现低后坐发射目的,又能满足Eyy≤1.6且Exx≤1,达到武器高精度的指标。

5 结束语

建立了采用首发浮动发射技术的GMG刚柔耦合发射动力学模型,并进行20连发射击过程的动力学仿真计算。

①建立的仿真模型是正确合理的,可以有效预测高初速GMG的射弹散布。

②基于首发浮动方式发射的GMG在20连发射击过程中,在前3发射击过程中射击稳定性较差,但在第5发后趋于稳定,弹着点向散布中心收敛;最大后坐力出现在前两发过程中,采用首发浮动发射技术可以将武器架座力控制在3 500 N内,达到武器低后坐发射高速榴弹的目的。

③增大浮动行程、降低浮动簧刚度,可以有效降低武器架座力;文中给出浮动参数的调节范围,对提升武器射击密集度、改善其发射性能有一定指导意义,高初速GMG试制过程中可参考文中给出的浮动参数范围进行调整。

④浮动解锁位置对GMG架座力、射击密集度、击发时间较为敏感,是GMG瞎火、后坐力出现异常的主要原因,在试制过程中要特别注意。

[1] 宋杰,廖振强,李佳圣,等.导气与枪管浮动混合式自动机自动机动力学特性研究[J].兵工学报,2014,35(6):753-761. SONG Jie,LIAO Zhen-qiang,LI Jia-sheng,et al.Dynamics characteristics of automatic mechanism for gas operated and floating barrel operated automatic action[J].Acta Armamentarii,2014,35(6):753-761.(in Chinese)

[2] 王亚平,徐诚,王永娟.火炮与自动武器动力学[M].北京:北京理工大学出版社,2014. WANG Ya-ping,XU Cheng,WANG Yong-juan.Dynamics of artillery and automatic weapons[M].Beijing:Beijing Institute of Technology Press,2014.(in Chinese)

[3] KANG K J,GIMM H I.Numerical and experimental studies on the dynamic behaviors of a gun that uses the soft recoil system[J].Journal of Mechanical Scicence and Technology,2012,26(7):2 167-2 170.

[4] 王文记,赵国豪,赵勇,等.国内外高炮浮动技术的现状与发展趋势[J].火炮发射与控制学报,2007(3):69-72. WANG Wen-ji,ZHAO Guo-hao,ZHAO Yong,et al.Present situation and development tendency of a gun floating technology home and abroad[J].Journal of Gun Launch & Control,2007(3):69-72.(in Chinese)

[5] 姚养无,王刚.大口径机枪低后坐浮动技术研究[J].华北工学院学报,2001,22(4):289-293. YAO Yang-wu,WANG Gang.Study of large caliber machine gun low recoil floating technology[J].Journal of North China Institute of Technology,2001,22(4):289-293.(in Chinese)

[6] 苑海威,薄玉成,王惠源,等.身管短后坐浮动自动机动力学仿真[J].火炮发射与控制学报,2010(1):52-55. YUAN Hai-wei,BO Yu-cheng,WANG Hui-yuan,et al.Dynamics simulation of floating automatic mechanism applied in short recoil barrel weapon[J].Journal of Gun Launch & Control,2010(1):52-55.(in Chinese)

[7] 杨军荣.基于软后坐技术的某自动迫击炮动力学分析[J].弹道学报,2006,18(1):63-67. YANG Jun-rong.Dynamic analysis of an auto mortar based on the soft recoil technology[J].Journal of Ballistics,2006,18(1):63-67.(in Chinese)

[8] 李魁武,王宝元.火炮射击密集度研究方法[M].北京:国防工业出版社,2012. LI Kui-wu,WANG Bao-yuan.Research methods of gun firing dispersion[M].Beijing:National Defense Industry Press,2012.(in Chinese)

[9] 李佳圣,廖振强,邱明,等.转管机枪在三脚架上不同方位射角发射动力学分析[J].弹道学报,2014,26(2):58-62. LI Jia-sheng,LIAO Zhen-qiang,QIU Ming,et al.Launch dynamics simulation of gatling gun shooting on a light tripod with different1 attitude angles[J].Journal of Ballistics,2014,26(2):58-62.(in Chinese)

[10] 李飞,王贵军.土力学与基础工程[M].武汉:武汉理工大学出版社,2012. LI Fei,WANG Gui-jun.Soil mechanics and foundation engineer-ing[M].Wuhan:Wuhan University of Technology Press,2012.(in Chinese)

Research on Launching Performance of GMG With High Muzzle-velocity Based on First-floating Technology

SONG Jie,QIU Ming,LIAO Zhen-qiang,HUA Hong-liang

(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)

To study the dynamic behavior of grenade machine gun(GMG)based on the first-floating technique,a rigid-flexible coupling multi-body dynamic-model was established,and 20-rounds firing process of GMG was carried out based on the dynamic model.The effect of floating parameters on firing accuracy was studied.The firing accuracy was calculated based on the external ballistic theory,and it was compared with the result by experimental test,and the dynamic model was validated.The effects of floating parameters on cradle force and firing accuracy were studied.The results show that the proposed dynamic model can predict the firing accuracy effectively.The optimal floating parameters can be matched reasonably to improve firing accuracy and reduce the recoil force.

grenade machine gun;high muzzle-velocity;floating parameter;firing dispersion;simulation

2017-01-22

国家自然科学基金项目(51375241,51376090)

宋杰(1986- ),男,博士研究生,研究方向为特种机械新原理新结构研究。E-mail:sj0501510127@126.com。

TJ25

A

1004-499X(2017)02-0070-08