质量监测指标如何细化
2017-07-17王红梅钟冬梅
王红梅 钟冬梅


试题质量的优劣直接关系到基础教育质量监测的科学性与权威性。小学数学质量监測双向细目表(以下简称“双向细目表”)是由知识维度与认知维度构成的二维关联表,是质量监测指标的具体化,是试题编制的依据。
为什么要编制双向细目表
提高试题编制的科学性。小学数学质量监测双向细目表,既明确了要测查的数学知识内容,也明确了学生所要达到的对应认知水平,以及要测查的内容和认知能力在项目巾所占比例。因此,对照双向细目表编制试题,不仅能将监测内容全覆盖,而且能克服试题编制中存在的主观性、随意性以及不够规范的现象,从而提高试题编制的科学性和客观性。
保证监测的内容效度。内容效度是指测验题月对有关内容或行为范围取样的适当性,也就是判断测验题目是否符合监测目标。小学数学质量监测双向细目表是根据小学数学质量监测的目的与内容,依据一定的原则,按照特定的程序编制而成的,它能较好地反映测试内容以及学生应达到的认知水平。因此,根据双向细目表编制试题能较好地保证质量监测的内容效度。
提供监测结果分析的依据。我们在编制数学质量监测试题时,如能保证每道题目均与双向细目表中的某项监测内容和认知水平相对应,那么在监测之后就可以对照双向细目表对参与监测学生的学业水平作出科学分析。
编制双向细目表的依据
双向细目表编制的依据是《义务教育数学课程标准(2011年版)》,并且对学生的数学学习和教师的数学教学起到导向作用。
编制双向细目表应从“以知识为本”走向“以人为本”,并非仅定位于对数学知识识记的考查,而应体现学生终身发展和可持续发展的成长诉求,实现“培养学科核心素养”的目标。而且要符合测量领域的专业化要求,能够有效地反映和监测出小学生的数学学业水平。
双向细目表编制的出发点是“公平”,即学生的不同学习背景不能影响监测的结果。同时,试题编制要符合数学学科特点和小学生的认知发展规律。
双向细目表的编制既要以数学课程标准为依据,又要体现国际上相关领域研究的现状和趋势;既要体现本地区小学数学教育的实际,又要与国家对数学质量监测的要求接轨。同时,要在吸收国内外编制数学双向细目表成果的基础上敢于创新,进一步推进数学双向细目表研究的开展。
如何编制双向细目表
首先是知识维度设计。知识维度是指数学课程标准中知识领域的核心概念和重要原理、法则。比如,M市四年级数学质量监测的知识维度是依据课程标准、各区县所使用的教材以及我们对知识的分类设定的。由于M市各学校四年级使用的教材有人教版和西师版,部分内容编排的顺序不同,本着公平适切原则,我们选择相同的内容作为三级指标进行测试。经过调查分析,我们制订了M市四年级数学质量监测知识维度细目表(见表1),反映核心内容的组织结构和地位。
其次是认知维度设计。认知维度是学生认识和理解数学以及从事数学活动所达到的操作水平反映。依据布卢姆教育目标分类法,学习借鉴国内外相关数学质量测评项目的经验,结合M市经济背景、教育期望值和教育现状,遵循小学数学质量监测双向细目表编制的原则,我们把M市四年级数学质量监测的认知维度设定为了解、理解、应用、创新四个水平(见表2)。比如,奇思在光盘上刻录了5段视频,每段视频所用的时间如表3所示,试题属性如表4所示。估计—下他刻录5段视频所需要的时间,并解释你的结果。
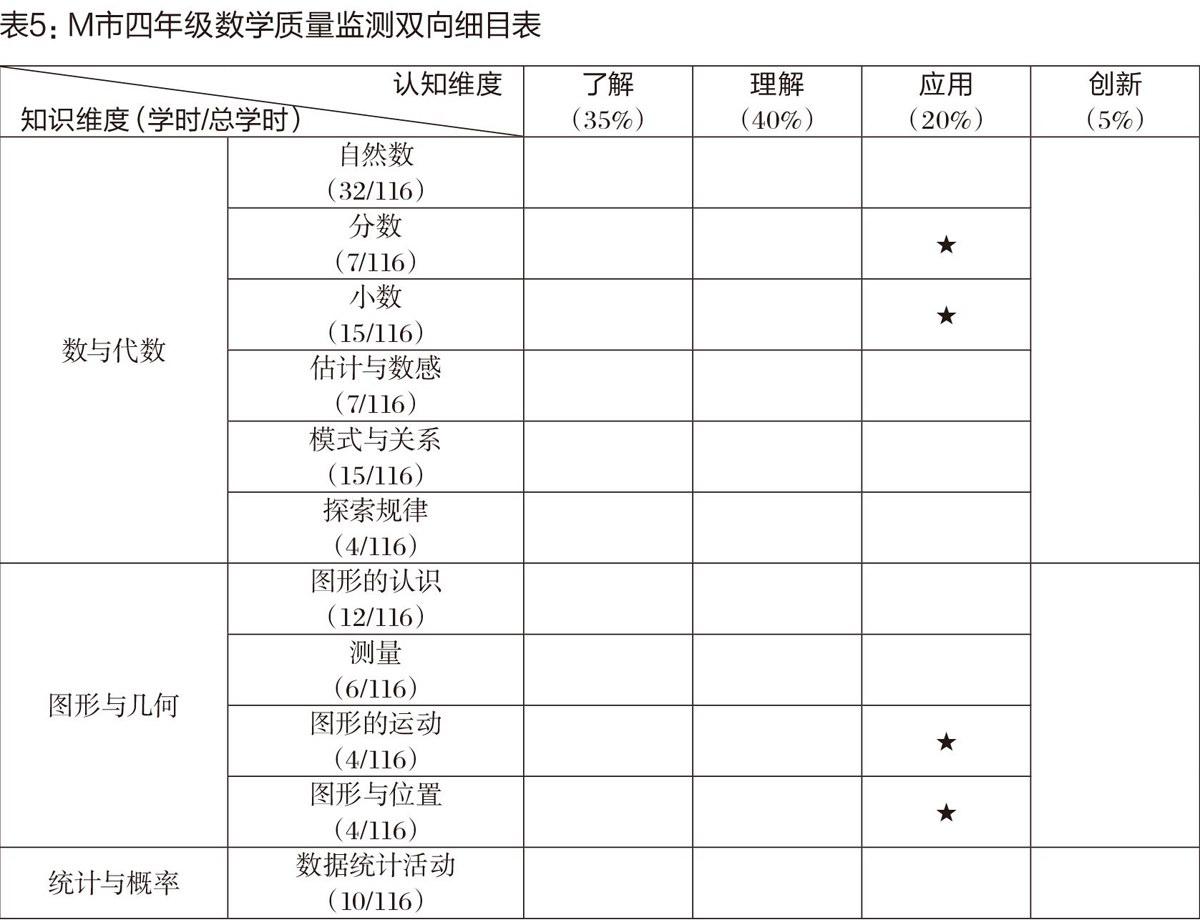
再次是双向细目表设计。我们将知识维度细分表和认知维度细分表合并形成了命题的双向细目表。按照质量监测试题整体难度系数控制在o.75-0.85之内的惯例,将了解、理解、应用、创新四个认知层次的试题比例确定为35%:40%:20%:5%。表5是M市四年级数学质量监测双向细目表(★处不命题)。
根据知识维度和认知维度各指标的权重,可计算每项知识在不同认知水平上所分配到的试题数目和分数。其中,试题的总数目参量指标N和试题总分参量指标S通常由命题专家根据监测目标确定。该表的行与列的权重数据之积可称为项目参数Cij,当试题数目和分数在知识维度和认知维度上呈均匀分布时,各项测评内容在每个认知水平上的试题数为N.Cij,得分为s.cij。如果M市四年级数学质量监测试题的总数目为30,那么自然数在了解层次的试题数为30x116/32x35%≈3。当一套试卷难以实现内容与认知能力的全覆盖时,可将未覆盖的部分参数值分配到其他项目单元格。
