点核积分计算6711型125I籽粒源剂量参数

孟贝蒂 曹 振 石翠燕 崔海平

1（中国原子能科学研究院 北京 102413）2（原子高科股份有限公司 北京 102413）3（同方威视技术股份有限公司 北京 100084）4（清华大学 工程物理系 北京 100084）

点核积分计算6711型125I籽粒源剂量参数

孟贝蒂1,2曹 振3,4石翠燕2崔海平1,2

1（中国原子能科学研究院 北京 102413）2（原子高科股份有限公司 北京 102413）3（同方威视技术股份有限公司 北京 100084）4（清华大学 工程物理系 北京 100084）

使用点核积分方法计算6711型125I籽粒源参数，根据美国医学物理学家协会(American Association of Physicists in Medicine, AAPM) TG-43U1号报告推荐的剂量参数计算公式，可以获得6711型125I籽粒源各参数。与AAPM TG-43U1推荐值比较，剂量常数相差6.76%，径向剂量函数值（不包括0.1 cm、0.15 cm、0.25 cm）最大相差2.27%，最小相差0.02%；与MCNP5 (A General N-Particle Transport Code, Version 5)方法计算结果比较，剂量常数相差6.19%，径向剂量函数值（不包括0.1 cm、0.15 cm、0.25 cm）最大相差6.65%，最小相差0.06%。结果与推荐值符合较好，证明点核积分能够应用于籽粒源剂量参数计算。

点核积分方法，剂量学参数，125I籽粒源

目前，多种类型的125I籽粒源广泛应用于永久性植入治疗肿瘤。125I籽粒源发射低能光子治疗肿瘤，具有将剂量精确地沉积在肿瘤细胞中，而不伤害肿瘤外围正常组织的优势[1-2]。

由于籽粒源治疗肿瘤主要是利用其周围剂量分布性，所以为了取得好的治疗效果，还必须知道籽粒源剂量分布情况。通过籽粒源剂量参数计算即可得到籽粒源在组织中的剂量分布，而籽粒源剂量参数可通过蒙特卡罗方法计算获得。目前，国际上采用较多的蒙特卡罗程序为MCNP5 (A General N-Particle Transport Code, Version 5)、MCNPX (Monte Carlo N-Particle eXtended)、EGSnrc (NRC’s electron gamma shower)、FLUKA (FLUktuierende KAskade)和GEANT4 (for GEometry ANd Tracking)等。以上程序均基于蒙特卡罗方法，其计算时间均较长，不能完成快速获得剂量参数结果的任务。本文将采用完全不同于蒙特卡罗方法的一种计算方法（SCALE6.1[3]中的点核积分模块QADS (Quick and Dirty Shielding)）对籽粒源剂量参数计算，验证点核积分是否能够快速有效地计算籽粒源剂量参数。

1 材料和方法

1.1 SCALE6.1程序介绍

SCALE为橡树岭国家实验室(Oak Ridge National Laboratory, ORNL)开发和维护的用于核安全分析和设计的综合模型和模拟套件程序包。最初，SCALE由美国核管制委员会(Nuclear Regulatory Commission, NRC)发起和开发，现在由NRC和美国能源部(Departement of Energy, DOE)支持和维护。SCALE提供全面的认证、用户友好的工具套件处理反应堆临界安全、反应堆物理、放射性屏蔽、放射源的参数描述、灵敏度和不确定度分析。本工作将使用其中的QADS模块对籽粒源进行剂量参数计算。

1.2 6711型籽粒源

本工作中使用6711型籽粒源来自文献[4]，由长为0.45 cm、直径为0.08 cm的圆柱体银棒作为内核，银棒表面涂125I放射性物质，外面由钛包壳包围，籽粒源长轴两端的焊点近似为半球。具体形状如图1所示。

图1 6711型125I籽粒源长轴方向切面Fig.1 Longitudinal view of model 6711 125I seed source.

1.3 籽粒源相关参数

使用的125I γ射线能谱数据取自文献[5]，使用的材料成分来自文献[6]，其中银的密度为10.5g·cm-3；钛的密度为4.54 g·cm-3；空气密度为0.001205 g·cm-3，其中C (0.000124)、N (0.755268)、O (0.231781)、Ar (0.012827)，括号内为质量份额。液态水的密度为1 g·cm-3，其中：H (0.111898)、O (0.888102)。

2 剂量参数和蒙特卡罗模拟

2.1 剂量参数计算公式

根据AAPM TG43U1报告内容[5]，可以得到籽粒源剂量和参数计算公式，其中：籽粒源参数剂量率常数Λ、径向剂量函数g(r)和各向异性函数F(r,θ)可以通过蒙特卡罗计算得到。剂量率常数Λ计算式：

式中：SK为空气比释动能强度，cGy·h-1·cm2（用U表示）；Λ为剂量率常数，cGy·h-1·U-1；D(r,θ)为某点上的剂量率；r表示离籽粒源几何中心的距离；θ表示与籽粒源长轴的夹角。D(r0,θ0)表示标准位置的剂量率，标准位置（参考点）如图2所示。其中：r0=1；θ0=π/2；L为活性长度。

径向剂量函数g(r)和各向异性函数F(r,θ)计算：

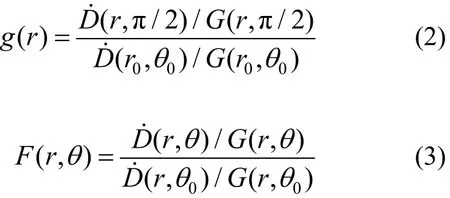
式中：G(r,θ)为几何函数，具体意义和计算方法见文献[5]。G(r,π/2)表示θ0=π/2时的几何函数值。D˙( r,θ)表示在某点上的剂量率，D˙( r,π/2)表示θ0=π/2时的剂量率。

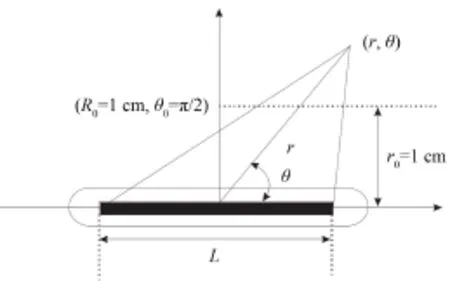
图2 剂量参数计算的极坐标系统Fig.2 Polar coordinates system used for dose parameter calculation.

2.2 点核积分计算和结果比较

2.2.1 点核积分计算

QADS能灵活设置放射源问题，不仅能模拟面源，还能模拟三维空间中任意形状和限制的放射源。大部分类型放射源能够在输入文件中直接写入代码描述。处理复杂放射源问题，还需要充分理解放射源的设置和配置。放射源描述代码包括总体归一化参数、空间网格和网格点空间分布一致性、能量结构和能谱形状一致性、放射源指定的坐标系统等。放射源几何偏离中心或者为复合源情况，使用笛卡尔(Cartesian)坐标系统。对于放射源几何偏离或复合源情况，可以描述一个整体的放射源几何，包括需要设置放射源整体，然后通过将非放射源存在区域设置为零权重，让此区域没有放射源存在。本工作将采用此种方法，先设置放射源几何为长0.3 cm、半径0.025 cm的圆柱体源，然后将圆柱体源进行网格划分，设置银棒表面权重为1，内部权重为0，达到设置圆柱体面源的效果。

2.2.2 剂量率常数Λ

使用SCALE版本为SCALE6.1[3]，sequence specification record:=qads。在Windows7 (32 bit)下运行。计算中源强度粒子数设置为1 s-1。单次模拟计算时间为5.94 s。空气比释动能计算将籽粒源放入半径为1.3 m的真空球体中，使用内径99cm、外径130 cm的球壳作为比释动能记录单元，内部填充材料为干燥空气。采用AIR ABS剂量计算卡记录比释动能。得到空气比释动能为3.816×10-14Gy。计算参考点(0°, 1 cm)处剂量吸收剂量，将籽粒源放入半径为1m充满液态水的球体中。得到参考点位置剂量为3.433×10-14Gy。根据式(1)计算可得6711型125I剂量率常数为0.900 cGy·h-1·U-1。与AAPM TG-43U1中6711型籽粒源剂量率常数推荐值0.965cGy·h-1·U-1相差6.76%。与MCNP5[7]结果0.959 cGy·h-1·U-1比较相差6.19%。可见，点核积分方法计算结果与推荐值符合较好，与蒙特卡罗方法计算结果相差不大。

2.2.3 径向剂量函数

QADS计算径向剂量函数模型为将籽粒源放入半径为1 m的充满液态水的球体中。其中记录吸收剂量为点位范围为0.10-10.00 cm。采用AIR ABS剂量计算卡记录吸收剂量。得到径向剂量函数见表1。

表1 径向剂量函数Table 1 Radial dose function g(r).

由表1可知，本实验与TG-43U1推荐值都符合较好（除0.1 cm、0.15 cm、0.25 cm），与TG-43U1的推荐值相比，相对偏差范围为0.02%-2.27%。与MCNP5方法计算结果比较，径向剂量函数值（不包括0.1 cm、0.15 cm、0.25 cm）最大相差6.65%，最小相差0.06%。可以看出，除了几个特别近的点外，其余点计算精度完全可以满足籽粒源剂量参数参考要求。将QADS计算结果进行5次多项式拟合，得到经验公式如下：

式中：a0=1.09936；a1=-4.45235×10-2；a2= -7.88919×10-2；a3=-1.88772×10-2；a4= -1.73590× 10-2；a5=5.79666×10-5。相关系数R=0.99992，残差平方和(Sum of Squares for Error, SSE)为2.79683×10-4，此式(4)使用范围为r=0.5-10.0cm。显然，排除离籽粒源较近几个点外，符合很好。相关系数值很高，同时残差平方偏小。

2.2.4 各向异性函数

QADS计算径向剂量函数模型为将籽粒源放入半径为1 m的充满液态水的球体中。各向异性函数计算点位为离籽粒源中心距离分别为0.5 cm、1 cm、2 cm、3 cm、4 cm、5 cm，对于相同距离角度从0°-90°分布，共66个点位。采用AIR ABS剂量计算卡记录吸收剂量。结合计算结果和式(3)得到径向剂量函数如表2所示。

表2 各向异性函数Table 2 Anisotropy function F(r,θ).

表2即为点核积分计算各向异性函数结果，为了能获得与AAPM TG-43U1推荐值之间相对偏差更加直观的效果，将此结果与推荐值比较，做出相对偏差如图3所示。

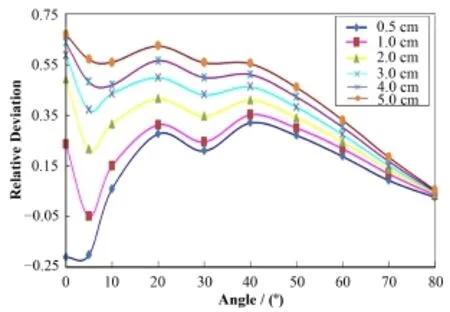
图3 相对偏差Fig.3 Relative deviation.

根据图3可以看出，点核积分计算结果与AAPM TG-43U1推荐值比较具有明显的趋势，随着距离和角度的增加，相对偏差明显减小。距离大于2 cm时，均能满足相对偏差小于30%的水平。但是由于其规律性明显，如果进行相应的修正，可以得到较理想结果。

3 结语

本工作对籽粒源剂量参数理论计算进行了一次新的尝试，采用QADS的方法对籽粒源剂量参数进行计算，寻找籽粒源剂量参数计算新的方法。根据AAPM TG-43U1推荐，采用QADS计算6711型125I籽粒源剂量参数，并将QADS计算结果与TG-43U1推荐值比较，得到剂量率常数(0.900 cGy·h-1·U-1)与AAPM TG-43U1中6711型125I籽粒源推荐值0.965cGy·h-1·U-1相差6.76%，与MCNP5结果0.959cGy·h-1·U-1比较相差6.19%。径向剂量函数g(r)结果与TG-43U1推荐值符合很好，与TG-43U1比较，相对偏差范围为0.02%-2.27%（除0.1 cm、0.15cm、0.25 cm），与MCNP5方法计算结果比较，径向剂量函数值（不包括0.1 cm、0.15 cm、0.25 cm）最大相差6.65%，最小相差0.06%。各向异性函数F(r,θ)值与TG43U1推荐值比较，随着距离和角度的增加，相对偏差明显减小。综上所述，QADS计算6711型125I籽粒源剂量参数结果，与AAPM TG-43U1推荐值虽然有些偏差，但是总体情况符合较好，如果对各向异性函数进行相应的修正，能得到较理想的结果。能够为籽粒源剂量参数研究提供理论计算依据，同时可以作为籽粒源应用于临床治疗的参考参数。

1 曹振, 阮锡超, 孟贝蒂, 等. MCNP5与EGSnrc比较计算125I种子源剂量参数[J]. 核技术, 2014, 37(2): 020201. DOI: 10.11889/j.0253-3219.2014.hjs.37.020201. CAO Zhen, RUAN Xichao, MENG Beidi, et al. Determination of dosimetric parameters for125I seed source using MCNP5 and EGSnrc MC codes[J]. Nuclear Techniques, 2014, 37(2): 020201. DOI: 10.11889/j. 0253-3219.2014.hjs.37.020201.

2 Babaheidari A E, Shamsaee M, Ahmadi P. Determination of dosimetric characteristics of a new design125I brachytherapy source with the Monte Carlo code MCNPX[J]. Radiochemistry, 2014, 56(3): 296-301. DOI: 10.1134/S1066362214030126.

3 SCALE: a comprehensive modeling and simulation suite for nuclear safety analysis and design (Version 6.1)[R]. ORNL/TM-2005/39, Radiation Safety Information Computational Center, Oak Ridge National Laboratory, 2011.

4 Nath R, Anderson L L, Luxton G, et al. Dosimetry of interstitial brachytherapy sources: recommendations of the AAPM radiation therapy committee task group No.43[J]. Medical Physics, 1995, 22(2): 209-234. DOI: 10.1118/1.597458.

5 Rivard M J, Coursey B M, DeWerd L A, et al. Update of AAPM task group No.43 report: a revised AAPM protocol for brachytherapy dose calculations[J]. Medical Physics, 2004, 31(3): 633-674. DOI: 10.1118/1.1646040.

6 Hubbell J H, Seltzer S M. Tables of X-ray mass attenuation coefficients and mass energy-absorption coefficients 1 keV to 20 MeV for elements Z=1 to 92 and 48 additional substances of dosimetric interest[R]. Gaithersburg, MD, United States: National Institute of Standards and Technology-PL, Ionizing Radiation Division, 1995.

7 曹振, 李飒, 张文在, 等. 6711型125I种子源剂量参数的蒙特卡罗研究[J]. 核技术, 2012, 35(5): 361-364. CAO Zhen, LI Sa, ZHANG Wenzai, et al. M-C simulation of dosimetric characteristics of model 6711125I seed source[J]. Nuclear Techniques, 2012, 35(5): 361-364.

Determination of dosimetric characteristics for the model number 6711125I seed source with the point-kernel method

MENG Beidi1,2CAO Zhen3,4SHI Cuiyan2CUI Haiping1,2
1(China Institute of Atomic Energy, Beijing 102413, China) 2(Beijing Atom High Tech Co., Ltd., Beijing 102413, China) 3(Nuctech Company Limited, Beijing 100084, China) 4(Department of Engineering Physics, Tsinghua University, Beijing 100084, China)

Background： The125I brachytherapy source has become a popular treatment option in the treatment various tumors, in order to reduce the risk of surrounding normal tissue, it is important to know the dosimetric characteristics of seed source. Purpose： The aim is to develop a reliable and saving time method for calculating the dosimetric parameters of seed source. Methods： Dosimetric parameters (dose rate constant, radial dose function and anisotropy function) of the model number 6711125I seed source are calculated with point-kernel method following American association of physicists in medicine (AAPM) TG-43U1 recommendations. Results： The result was compared with the relative data recommended by AAPM TG-43U1 and Monte-Carlo (M-C) method. Dose rate constant with AAPM was in agreement with 6.76%, and that with M-C is 6.19%; radial dose function (except 0.1 cm, 0.15 cm and 0.25 cm) with AAPM is within 0.02%-2.27%, and that with M-C is within 0.06%-6.65%. Conclusion：The point-kernel method can be applicable to calculate the dosimetric characteristics of seed sources.

Point-kernel integration method, Dosimetric parameters,125I seed source

MENG Beidi, female, born in 1988, graduated fromChina Institute of Atomic Energy with a master’s degree in 2013, doctoral student, focusing on nuclear technology and applications

CUI Haiping, E-mail: cui-hp@hotmail.com

date: 2017-02-20, accepted date: 2017-03-28

TL929

10.11889/j.0253-3219.2017.hjs.40.070501

孟贝蒂，女，1988年出生，2013年于中国原子能科学研究院获硕士学位，现为博士研究生，研究领域为核技术及应用

崔海平，E-mail: cui-hp@hotmail.com

2017-02-20，

2017-03-28