四节点四边形网格单元中一种新的云图生成算法

【摘要】 在三节点三角形网格单元基础上，分析四节点四边形单元特点，提出一种新的云图算法，可以有效提高云图生成效率。首先将等值线对四边形网格单元的切割过程划分为四种基本形式，又将每种基本形式的所有可能处理路径一一分析处理。其次针对四边形网格单元可能存在的二义性问题做专门讨论，简化了处理流程。该算法已在项目中实际应用，应用结果表明该算法是准确和高效的。

【关键词】 分割穷举算法 四节点四边形网格单元 云图 等值线 等值多边形

一、引言

三節点三角形网格单元中的云图分割穷举算法，在作者之前的文章中已经详细论述过[1]。四节点四边形网格单元也是一种应用广泛的单元类型，其中的云图技术既有和三角形单元相同之处，也有他的特点。相同之处在于，四节点四边形单元中的分割穷举算法仍然是基于等值线网格序列法[1]的，其次等值线对网格单元的分割仍然按照一定的规律排列，所以我们仍旧可以利用分割穷举的思想对四边形网格单元中的等值线数据进行排序，最终生成四边形单元中的等值多边形数据，最终形成云图数据。而区别首先在于四节点网格单元中等值线对网格单元的划分形式更复杂，其次在于由于等值线数据二义性[2]的存在，对等值线数据的排序更复杂。

二、问题描述

和三角形网格类似，四边形网格中的所有单元经过网格序列法处理，已经生成了等值线数据，并以网格单元为单位组织存储。如图1所示，为四边形网格中几种可能 的等值 线分布形式。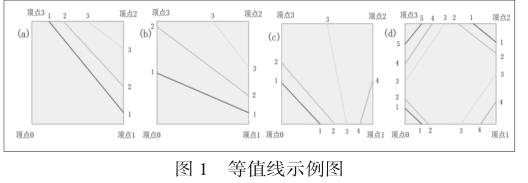

可以证明，与三角形网格单元类似，四边形网格单元内部等值点的排列仍然符合如下下面两条定理：

[定理1] 等值点按照场值由小到大排列。

[定理2] 等值点按照所在网格边编号由小到大排列。

这里对网格边编号定义为：由顶点0和顶点1所夹边为边0，由顶点1和顶点2所夹边为边1，由顶点2和顶点3所夹边为边2，由顶点3和顶点0所夹边为边3。例如图1（a）中，场值最小的等值线1与边1和边2的交点为第1和第2个等值点，场值次小的等值线2与边1和边2的交点为第3和第4个等值点，等等依此类推。

基于上述两点规律，在没有二义性时，四边形网格单元与三角形单元类似，其中等值线与网格的相交必定是按照一个固定方向进行的，与图1（a） 、1（b）和图1（c）中所示。但是与三角形网格单元不同，四边形网格中一条等值线可能与网格单元存在四个交点。这就是四边形网格中二义性问题，二义性会带来等值线走向判断的问题，该问题已有很好的解决方案，例如文献中提到的投影不相交原理[2]。但二义性同时会导致等值线与四边形网格不按固定方向排列的问题，这与三角形单元形成了最大的区别。例如图1（d）中，场值最小的等值线1与边0、1、2和3的有四个交点。根据二义性判断，将其中边0和3上的两个等值点连接形成一条等值线段，将另外两个等值点连接形成另一条等值线段。即图1（d）中标号为1的两条等值线段，下面标号2的等值线段同理产生。需要注意的是，标号为3的等值线根据投影不相交原理将边1和2上的两个等值点连接形成一条等值线段，将另外两个等值点连接形成另一条等值线段。此时等值线从原来包围顶点0、2的情况突变为包围顶点1、3的情况，而等值线不再按照之前的方向与网格单元相交。对这个由二义性引起的等值线相交方向突变问题的解决是四边形网格中分割穷举法的一个关键，后面专门讨论了一种“退步处理”的思路。

三、四节点四边形单元分割穷举算法

3.1分割形式

四边形单元被等值线分割的形式比较复杂。首先，仍然存在这样的情况：某些网格单元恰好夹在两条等值线之间，该网格单元没有被任何等值线分割。此时我们可以将整个四边形网格单元看成一个完整的等值四边形。

四边形网格单元被若干等值线分割的情况讨论如下。

我们依照第一条等值线的场值和网格单元四个顶点的场值的大小关系，将分割形式划分为四种基本形态：“三小一大”型、“两小相邻”型、“两小相隔”型和“一小三大”型。

1） “三小一大”型：四边形网格的四个顶点中有一个顶点的场值比第一条等值线的场值大，其余三个顶点的场值比第一条等值线的场值小。如图1（a）所示。2） “两小相邻”型：四边形网格的四个顶点中有两个相邻顶点的场值比第一条等值线的场值大，其余两个顶点的场值比第一条等值线的场值小。如图1（b）所示。3） “一小三大”型：四边形网格的四个顶点中有三个顶点的场值比第一条等值线的场值大，剩余一个顶点的场值比第一条等值线的场值小。如图1（c）所示。4）“两小相隔”型：四边形网格的四个顶点中有两个相隔顶点的场值比第一条等值线的场值大，其余两个相隔顶点的场值比第一条等值线的场值小。如图1（d）所示。

“三小一大”型和“两小相邻”型与三角形网格单元中“两小一大”型和“一小两大”型非常类似，等值线必定按照一个固定方向排列，因此对这两种分割方式的处理也可以参考三角形网格的两种处理方式[1]。而“两小相隔”型和“一小三大”型中由于可能存在二义性，因此等值线排列方式比较复杂，其处理方式也随之复杂。

四边形网格中“三小一大”型的处理算法如下：

首先第一条等值线和三个较小的网格顶点围成一个等值五边形，其包含5个顶点。例如图1（a）中由等值线1的两个端点和网格顶点0、1、3围成的等值五边形。

其次循环处理，每条等值线的两个等值点和之前的一对等值点围成一个等值四边形，例如图1（a）中由等值线1和2的四个端点围成的等值四边形。最后处理完所有等值点后，将最后一对等值点和剩下的一个网格顶点围成一个等值三角形，例如图1（a）中由等值线3的两个端点和网格顶点2围成的等值三角形。

四边形网格中“两小相邻”型的处理算法如下：

首先，第一对等值点与较小的两个网格单元顶点围成一个等值四边形。其次循环处理，每次判断下一对等值点对网格单元的分割方式。如果分割仍然是“两小相邻”，那么将当前两个等值点和前一对等值点围成一个等值四边形，例如图1（b）中由等值线1、2围成的等值四边形；如果当前等值线对网格单元的分割变成“三小一大”型，说明当前等值线跨过某个单元顶点，此时将当前两个等值点和前一对等值点及被他们所夹的网格单元顶点围成一个等值五边形，例如图1（b）中由等值线2、3和网格单元顶点3围成的等值五边形。如果分割方式已变成“三小一大”型，需要跳出当前循环，如果后续还有等值线，则按照“三小一大”型处理。

3.2“一小三大”型的处理

对于“一小三大”型，这种分割形式的后续发展有多重可能，首先该网格单元有可能在与后续的某条等值线相交时直接变化为“三小一大”型或“两小相邻”型，这样之后的排列仍然可以按照“三小一大”型或“两小相邻”型的方式处理。当变化为“三小一大”型时，意味着相邻两条等值线中间夹着一个等值六边形，即由前后两对等值点和所夹的两个网格顶点组成的六边形。例如图1（d）中，如果没有等值线3，则由等值线2、4和顶点2、3围成一个等值六边形。当变化为“两小相邻”型时，意味着相邻两条等值线中间夹着一个等值五边形，即由前后两对等值点和所夹的一个网格顶点组成的五边形。例如图1（d）中，由等值线2、3和顶点3围成一个等值五边形。之后的处理按照前述“三小一大”型和“两小相邻”型的方式进行即可。“一小三大”型的处理难点主要在后期可能转化为“两小相隔”型。

当变化为“两小相隔”型时，某条等值线的场值大于两个对角网格顶点，小于另外两个对角顶点时，意味着此时单元与某个场值的等值线有四个交点，产生二义性。这样后续等值线与网格相交不再按照一个固定方向进行的，如图1（d）中所示。这时可以将程序流程转入“两小相隔”型的处理模块。此时需要知道哪些网格顶点已经被一条等值线包围，因此做如下“主顶点”定义。

[定义1] 主顶点：当四边形某顶点所在的两条边都有等值点存在，并且离该顶点最近的两个等值点恰好是某条等值线的两个端点，则称该四边形顶点为一个“主顶点”。

當程序流程转入“两小相隔”型的处理模块时，将当时的主顶点信息传入，并传入最后一条包围主顶点的等值线信息，以待后用。

3.3“两小相隔”型的处理

“三小一大”型和“两小相邻”型（包括从“一小三大”型变化过去的情况）中等值线对网格单元的切割总是按照一个固定的方向前进，这种固定的方向是上述处理的基础。但是对于“两小相隔”型（包括从“一小三大”型变化过去的情况），等值线对网格单元的切割方式不再按照固定顺序，而是有可能在某种情况下发生突变。

从“一小三大”型变化为“两小相隔”型的第一种可能情况是被后续等值点包围的仍然是原来的顶点和他的对角顶点，并在此种情况下结束。第二种可能情况是，先变为上述情况，然后变为“三小一大”情况。

第三种情况仍然是先变为第一种情况，然后由于二义性的存在后续的某条等值线不在包围原始的两个顶点，而包围另外两个顶点，并在此种情况结束。也可能最后变为“三小一大”情况。最后一种可能情况是，一进入“两小相隔”型即由于二义性的存在，改变了被包围的顶点，并在此种情况结束，或有可能最后变为“三小一大”情况。

开始就是“两小相隔”型的情况下，等值线可能的分割形式与上述情况相似，但是有两点不同。首先，不再有第一条在“一小三大”情况下产生的标号为1的等值线；其次，不存在第四种情况。无论上述哪种情况，经过分析发现，一旦由于二义性，被等值线包围的顶点发生变化，则等值线对网格单元的切割顺序即发生变化。没发生变化前，切割总是从两个角开始沿着对角线向里切割。当发生变化后，等值线开始沿着另外一条对角线向外不断切割。

四、结论

该算法已在作者所在项目中应用，事实证明该算法是准确和高效的。如图2所示，是一组实验数据所绘制的云图，左图为条纹云图，右图为光顺云图。该数据中包含3552个网格单元和16条等值线。测试计算机CPU为INTEL G630，主频2.7GHz，内存4G。云图计算和绘制时间的测试结果为1.76秒。当然本算法有进一步改进的可能，例如可以利用等参元变换对每条等值线进行插值，将现有的直线段式等值线优化成折线段式等值线，使绘图结果更美观。这些都是今后可能的研究方向。

参 考 文 献

[1] 杜小甫， 王成恩. 基于等值线数据的一种新的云图算法[J]. 东北大学学报（自然科学版）， 2013， Vol. 34 （5）： 624-627.

[2] 王成恩. 面向科学计算的网格划分与可视化技术[M]. 北京：科学出版社，2011：109-133.