纱线截面压缩变形仿真与验证
2017-07-12李冠志GONGHugh
李冠志, 赵 强, 汪 军, GONG Hugh
(1. 东华大学 纺织学院, 上海 201620; 2. 中国纺织科学研究院, 北京 100025; 3. 东华大学纺织面料技术教育部重点实验室, 上海 201620; 4. 曼彻斯特大学 材料学院, 曼彻斯特 M60 1QD)
纱线截面压缩变形仿真与验证
李冠志1,2, 赵 强1,2, 汪 军1,3, GONG Hugh4
(1. 东华大学 纺织学院, 上海 201620; 2. 中国纺织科学研究院, 北京 100025; 3. 东华大学纺织面料技术教育部重点实验室, 上海 201620; 4. 曼彻斯特大学 材料学院, 曼彻斯特 M60 1QD)
为了改进现有纱线条干均匀度测试仪在预测织物外观质量上的缺陷,对棉型平纹织物织造过程中的纱线截面面积、纱线截面周长、纤维空隙率、纱线压扁率, 纱线密度等纱线截面参数的变化建立分析模型并优选参数,并采用有限元分析和实验论证的方法,进一步分析织造过程中纱线截面面积及周长的变化。通过分析得出,在纱线到织物的织造变形过程中,纱线截面周长的变化远小于其截面面积的变化,纱线截面面积的变化率约是纱线截面周长变化率的2~3倍。通过对纱线截面椭圆长轴与其截面周长、截面面积分别进行相关性分析,得出纱线截面周长与椭圆长轴呈弱相关,纱线截面面积与长轴间无相关性。
纱线条干均匀度; 纱线压扁率; 有限元分析; 图像处理
纱线截面形状(纱线外观条干不匀)对织物外观有重要影响,在1969年Hearle教授认为纱线截面形状是不规则多边形[1],这种纱线截面形状的差异本质上是纱线径向上纤维分布不匀。单纱经历织造工序,受力拉伸、弯曲、扭转和压缩交织成织物后,纤维分布不匀现象加剧,其截面形状的变化将更大,从而进一步影响织物外观质量。
一直以来,利用单纱质量来实现织物质量的准确预测是极具挑战性的。USTER公司电容式纱线条干均匀度测试仪[2]测得的条干数据用于预测织物外观质量,单纱经过织造过程织成织物后,纱线截面的纤维根数基本不变,但是对织物外观造成影响的不仅有纱线中纤维根数,还有纤维间空隙,这二者共同决定了纱线外观直径;因此,电容式条干仪在预测织物外观质量方面不可避免地存在缺陷。为此,近年来业内各式电容式条干仪纷纷加装了测量纱线外观直径的光电模块用之于织物仿真[2],或利用图像式纱线外观测试分析仪器预测布面质量[3-5]。上述改进虽然预测效果略有提高,但尚不能完全满足生产实际要求。
究其原因,以往的方法均是纺纱厂从生产控制的视角来评价纱线综合质量,很少从织物外观角度来评价纱线外观质量,深究单纱经过织造过程后影响织物外观的纱线截面参数变化,这些参数是建立起由纱线质量到布面质量准确预测和一致性评价的关键。本文依据相关学者关于单纱纱线截面模型[6-8]、织物中纱线截面模型[9-13]和纱线压缩变形[14-15]的研究成果,结合纱线质量与布面质量的一致性评价需要,将单纱和织物中的纱线截面模型统一假定为椭圆形。通过研究织造过程中影响织物外观的纱线截面参数的变化,探索改进现有织物外观质量预测方法的新思路。
1 理论分析
1.1 理论分析及参数选取
在织造过程中,纱线截面受力拉伸、弯曲、扭转和压缩而变形,在这一过程中纱线截面参数是不断变化的,这些参数主要有纱线截面面积Sy、截面周长Sp、纤维空隙率Vf、纱线压扁率f, 纱线密度ρy,下面探究纱线这些截面参数在织物中的变化规律。
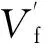

图1 纱线截面模型Fig.1 Yarn cross-section model. (a) Individual yarn; (b) Yarn in fabrics
假设织造前后纱线中的纤维不发生轴向的滑移,且纤维根数n,纤维截面积Sf,纤维密度ρf均不变。

(1)

综上可以看出,Vf、ρy均由Sy所决定。而Sp由Sy和f的共同决定,所以,这里纱线截面参数主要考虑Sy和纱线截面周长Sp即可。
Sy和Sp由最外围纤维排列所决定的,这里假设最外围纤维相互间紧密排列。此时,纱线截面形态的变化与外围纤维所围绕成闭合区域的纤维空隙率Vf有较大关系。图2示出纱线压缩形变分析。当闭合区域的Vf最小时:纤维如图2(a)所示紧密排列,在纱线受压变形过程中,外围纤维所拟合成椭圆截面后得到的Sp呈现增大趋势,Sy基本不变,如图2(b)所示;当闭合区域Vf最大时,外围纤维如图2(c)所示紧密环绕排列,纱线受压变形过程中,若外围纤维仍紧密排列,不向内部坍缩滑移,则最终Sp基本不变,Sy减小,如图2(d)所示;若发生坍缩内移,则最终Sp减小,Sy减小如图2(f)所示;交织过程中纱线形态应是形态1,形态2和形态3这3种情况之一。
Sy和Sp在织物中的变形主要是由纱线受力所造成的,这些力的作用时间和大小受到纱线性质、上机工艺、织物组织结构等较多复杂因素的影响。为了探究纱线在织造过程中截面参数的变化,下面以棉型织物为例利用有限元分析的方法初步探究。
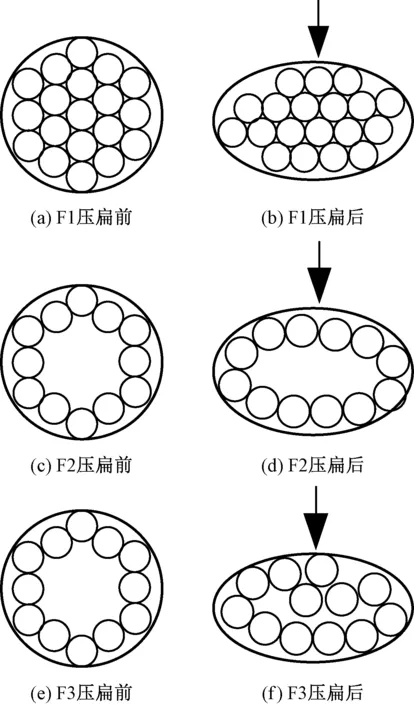
图2 纱线压缩形变分析Fig.2 Analysis of yarn compression. (a) F1 before compress; (b) F1 after compress; (c) F2 before compress; (d) F2 after compress; (e) F3 before compress;(f) F3 after compress
1.2 模型建立及仿真
建立织物模型时本文以18 tex的棉纱织造的平纹织物为参照样,其经向紧度16°,纬向紧度12°。假设构成织物的纱线是由60根纤维堆砌而成的,纱线截面模型长轴2a=0.2 mm,短轴2b=0.18 mm。Abaqus软件[16]中设置的纱线参数如表1所示,织物交织仿真应变云图见图3。定义纬纱方向3根纱线依次按交织规律相对运动,相对位移为0.42 mm。下面分析交织过程中时间对最中间经纱对交织点处纱线的截面周长和截面面积的影响,结果如图4所示。从该图中可看出在交织受压过程中,纱线截面周长的变化率小于截面面积。这里用极差系数(见下式)来表示交织前后的变化率,图4中,交织前后纱线周长减小了9.02%,而面积减小了27.67%。
(2)
式中:J为极差系数,Xmax为形变前后周长或面积最大值,Xmin形变前后周长或面积最小值。

表1 纱线参数设置Tab.1 Yarn parameters in abaqus
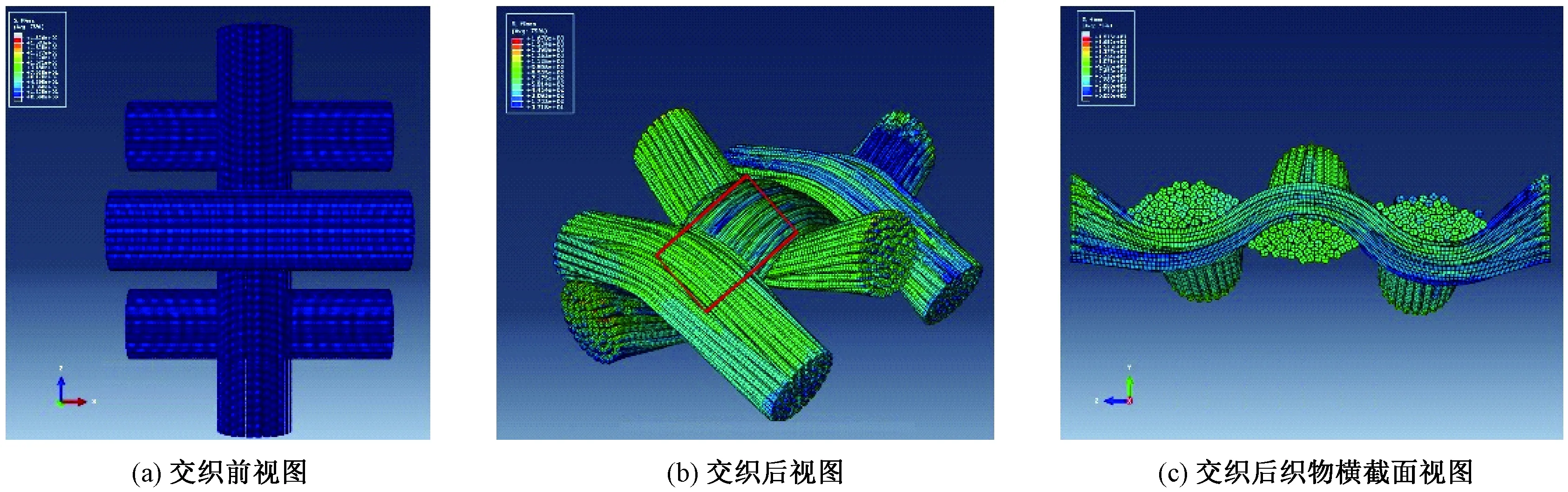
图3 织物交织仿真应变云图Fig.3 Contours of the fabric weaving modeling. (a) Before weaving; (b) After weaving; (c) Section view of weaved fabric.
交织完成后选取半个单胞进行分析,如图3(b)中红色框选部分所示,等间隔选取10个纱线截面,如图5所示,分别计算纱线截面周长和截面面积,同样得出了类似的变化规律,结果如图6所示,压缩前后纱线周长减小了7.54%,而面积减小了17.34%。
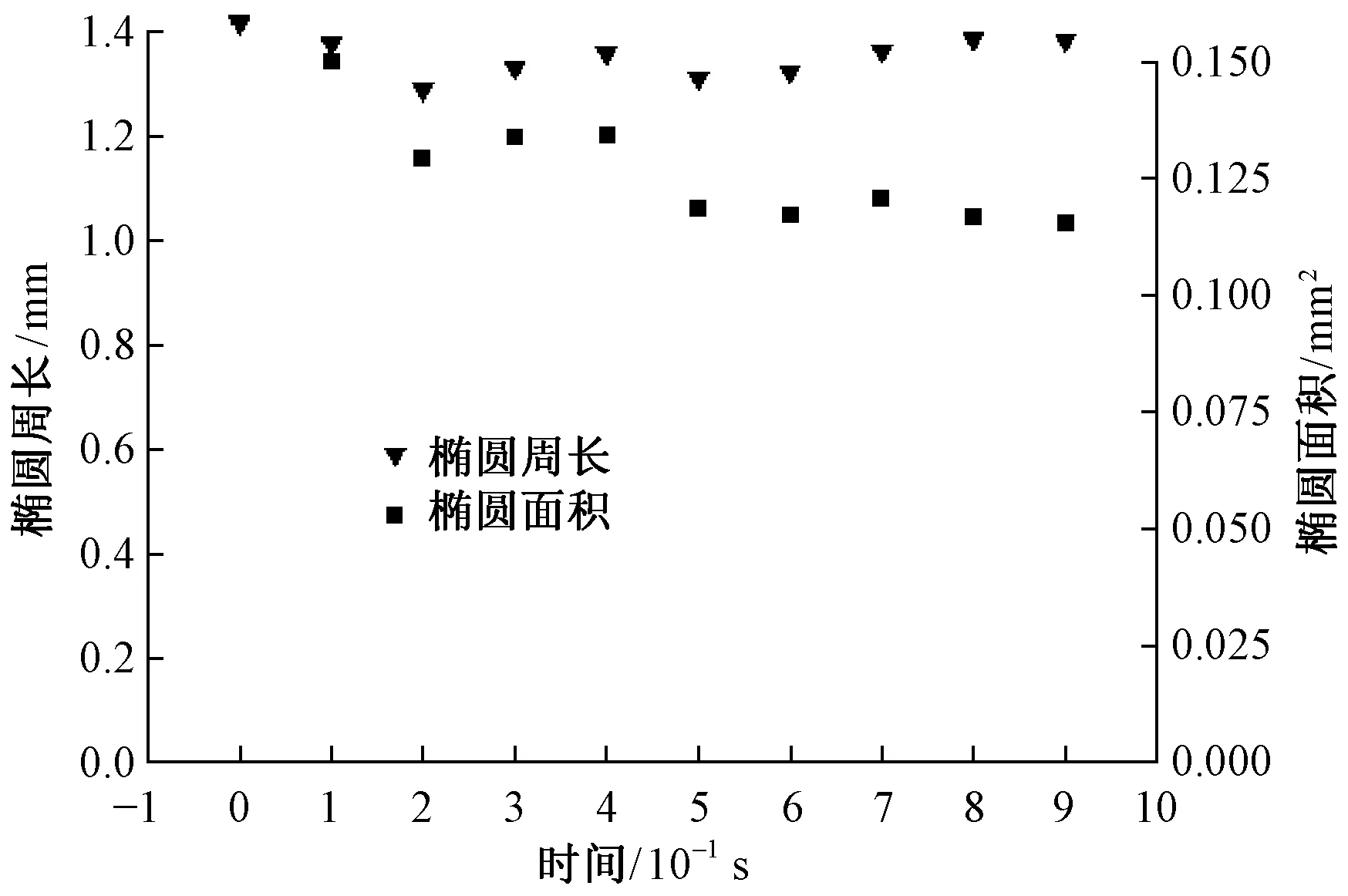
图4 织物交织过程中纱线截面参数随时间变化Fig.4 Yarn cross-section parameter variations with time during fabric weaving process.
2 实验部分
2.1 织物中纱线截面图像的获取
连续获取织造全部过程中的纱线截面变化是极其困难的,但考虑到纱线截面变形主要是与纱线受力有关,织物中单根纱线交织处和非交织处受力不同必然造成纱线截面形变不同。下面通过研究织物中纱线所处不同位置的截面形状变化来研究纱线截面周长和纱线截面面积的变化规律。
实验材料选用棉纱交织成的平纹织物,该织物由Bonas-Varitex织机织造,经纱紧度16°,纬纱紧度12°,纱线线密度18 tex,纱线捻度890 捻/10 cm,该纱线是由马克隆值为4.2的棉纤维纺制而成。为保证图像数据的非破坏采集,采用法国的同步辐射光源ESRF中ID19光束扫描织物,利用2 048像素×2 048像素分辨率的FReLoN相机对织物进行成像,图像分辨率为18 149像素,每幅图像对应的实物大小为2.8 mm×2.8 mm。下面随机选取1/2个单胞图像进行分析,图7所示。

图5 织物交织后同一纱线不同截面Fig.5 Different section views of the same yarn in fabric. (a) Section 1; (b) Section 2; (c) Section 3; (d) Section 4; (e) Section 5; (f) Section 6; (g) Section 7; (h) Section 8; (i) Section 9; (j) Section 10
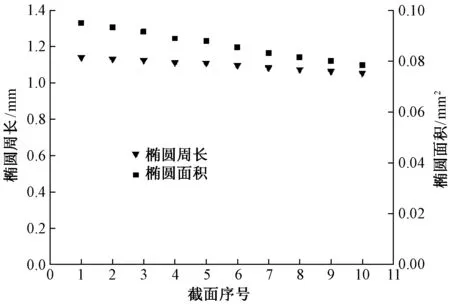
图6 交织为织物后同一根纱线纱线不同位置截面参数变化Fig.6 Yarn cross-section parameter variations at different section views of the simulated yarn

图7 织物中同一纱线不同位置截面形状变化Fig.7 Yarn cross-section parameter variations at different section views of the same yarn in a real fabric. (a) Section 1; (b) Section 2; (c) Section 3; (d) Section 4; (e) Section 5; (f) Section 6; (g) Section 7; (h) Section 8; (i) Section 9; (j) Section 10
2.2 纱线截面图像纱线周长和面积的提取
纱线截面图像首先进行中值滤波的降噪处理,二值化、闭运算后,为消除闭运算后图像有部分黏连。利用分水岭算法(watershed)再次分割,并调用imimposemi函数过滤掉一些特别小的局部最小分割区域。分割完成后然后调用bwareaopen函数消除较小的闭合面积,并选用canny算子进行边缘检测,从而得到清晰的纱线外沿轮廓。最后根据该轮廓调用fitellipse函数进行椭圆拟合,计算出椭圆长轴和短轴长度,流程如图8所示。

图8 纱线截面参数提取Fig.8 Extraction of yarn cross-section parameters: (a)Original; (b)Median; (c)Binaryzation; (d)Imclose; (e)Watershed; (f)Bwareaopen; (g)Eage detection; (h)Ellipse fitting
3 结果分析
对上述纱线截面1~10依次进行处理后,得到表2中数据,从表中f可以看出,f在交织点处最小,压扁最厉害;而两交织点中间最大,即该处更接近于圆形。f由交织点中间向交织点处移动的过程中呈现不断减小的趋势。在此过程中,椭圆纱线截面的面积和周长也呈减小趋势,由图9可以明显看出纱线截面周长的减小趋势相较于纱线截面面积则更为平缓。通过表2计算极差系数,交织前后纱线周长减小了17.33%,而面积减小了41.60%,与仿真结论趋势一致,但比仿真结果偏大,其原因是仿真过程中假定各纱线截面均相等,纤维截面为标准圆形且纤维间等距离堆砌,这些理想化假设与实际情况均有差异。
为进一步佐证,本文用同样方法计算了Hirai[14-15]中压缩纱线后纱线截面图像的纱线截面周长和纱线截面面积数据,得出5、50、1 000 cN这3种拉力下的纱线压缩前后纱线周长减小了12.24%,而面积减小了35.81%,这一变化趋势与在纱线压缩时表现出的特性保持一致,且与仿真结果趋势一致。

表2 织物组织中不同截面纱线截面参数Tab.2 Yarn cross-section parameters of different yarn cross sections in a fabric.
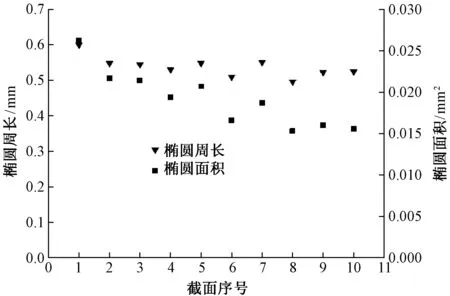
图9 纱线截面周长和纱线截面面积变化Fig.9 Yarn cross-section perimeter and area variations of section 1-10
织物中尤其经纬密较大的织物,其纱线在交织点处呈压扁状态,织物外观主要受到被压纱线截面的椭圆长轴影响[7]。下面分别对纱线截面周长和截面面积与纱线截面长轴进行相关性分析,图10示出纱线截面周长与椭圆长轴呈弱相关,相关系数R=0.2,而纱线截面面积与长轴无相关性,R=0.07。因此,纱线截面周长预测织物质量时相对于纱线截面面积更有优势。
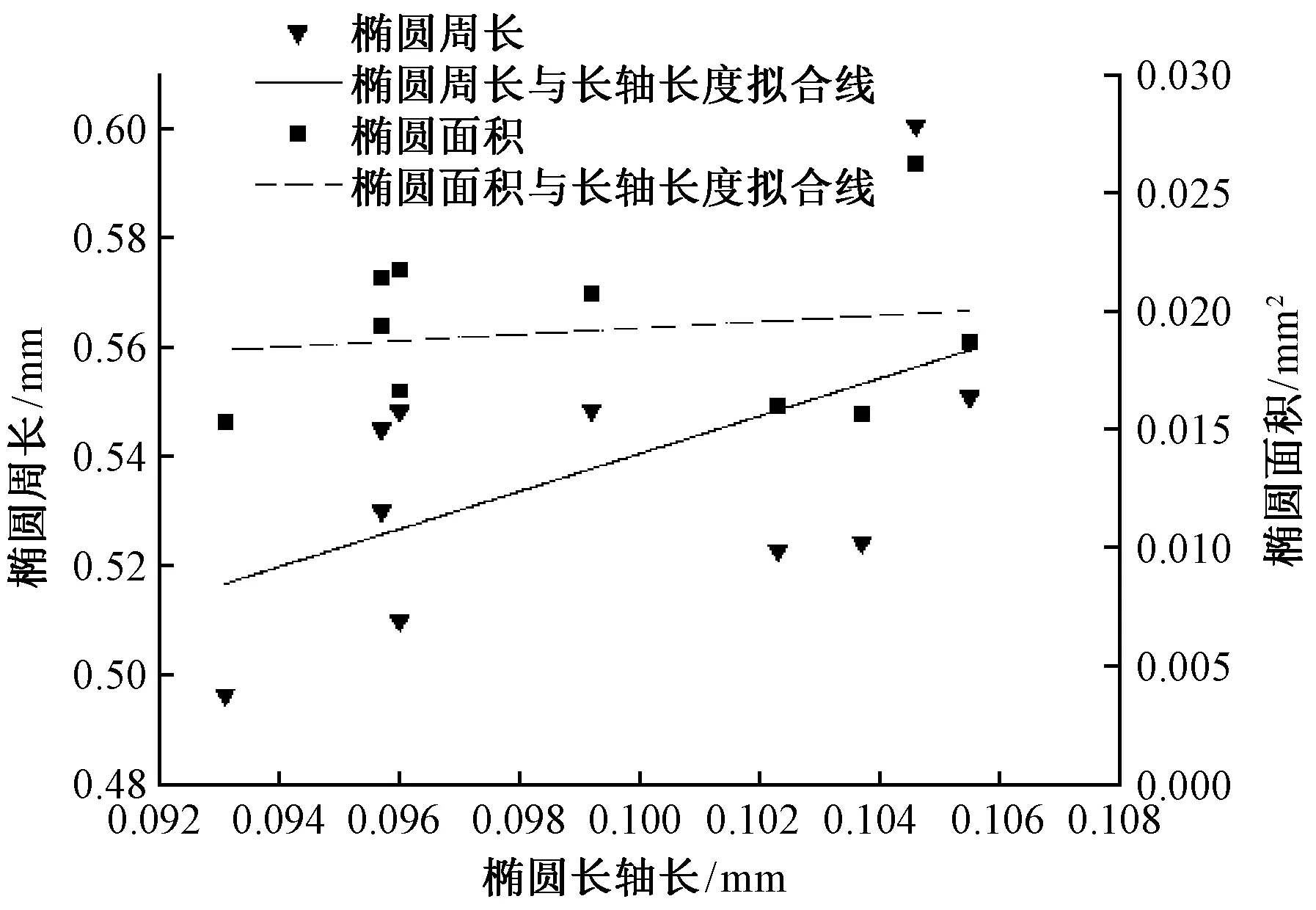
图10 纱线截面周长与截面面积与椭圆长轴相关性分析Fig.10 Correlation analysis of ellipse major axes with yarn cross-section perimeter and area of sections 1-10
4 结 论
在椭圆形纱线截面模型的基础上,本文根据有限元分析和实验论证,得出以下几点结论。
1)纱线在交织为织物受挤压变形的过程中,纱线外围纤维倾向于坍缩内移(形态3),纱线截面周长和截面面积在这一过程中均减小。
2)纱线交织受压变形过程中受影响的纱线截面参数中纱线截面面积、纱线截面周长、纤维空隙率、纱线压扁率, 纱线密度,最终可简化为纱线截面周长和纱线截面面积这两个参数。
3)截面周长和纱线截面面积在纱线到织物的变形过程中,纱线截面周长的变化远小于纱线截面面积的变化,纱线截面面积的变化约是纱线截面周长变化的2~3倍,纱线截面周长的变化率在8%~17%之间,纱线截面面积的变化率在17%~42%之间。
4)织物外观主要受到织物中被压纱线椭圆截面的长轴所影响,数据表明,纱线截面周长与椭圆长轴呈弱相关,纱线截面面积与纱线椭圆截面的长轴无相关性,纱线截面周长在预测织物质量时相对于纱线截面面积更有优势。
这些结论有助于改善纱线质量到布面质量客观一致性评价,对改进现有织物外观质量预测手段提供了新思路。
FZXB
[1] HEARLE J W, GROSBERG P, BACKER S. Structural Mechanics of Fibers, Yarns, and Fabrics[M]. New York: Wiley-Interscience, 1969:175-211.
[2] USTER®TESTER 5 Brochure[EB/OL]. [2016-05-01]. http://www.uster.com/fileadmin/customer/Knowle-dge/Textile_Know_How/Yarn_testing/U_T5_S800_High_sped_testing_in_01.pdf.
[3] Electronic inspection board[EB/OL].[2016-07-01]. http://www.lawsonhemphill.com/assets/lh-481-eib-s.pdf.
[4] 刘长伴. CTT在纱线综合质量评价中的应用研究[D]. 天津: 天津工业大学, 2007: 64-65. LIU Changban. The study of yarn comprehensive evaluation with CTT system[D]. Tianjin: Tianjin Polytechnic University, 2007: 64-65.
[5] CARVALHO V, GONÇPALVES N, SOARES F, et al. An overview over yarn mass parameterization me-thods[C]//Sensordevices 2011, The Second International Conference on Sensor Device Technologies and Applications. Nice: [s.n.]. 2011: 18-24.
[6] TSAI I, CHU W. The measurement of yarn diameter and the effect of shape error factor (SEF) on the measurement of yarn evenness[J]. Journal of the Textile Institute, 1996, 87(3): 496-508.
[7] GÜNAY M. Characterization and quantification of woven fabric irregularities using 2-D anisotropy measures[D]. NC: North Carolina State University, 2005: 74-75.
[8] HAMILTON J B. A direct method for measuring yarn diameters and bulk densities under conditions of thread flattening[J]. Journal of the Textile Institute Transactions, 1959, 50(12): 655-672..
[9] PEIRE F T. The geometry of cloth structure[J]. Journal of the Textile Institute Transactions, 1937, 28(3): 11-22.
[10] KEMP A. An extension of Peirce′s cloth geometry to the treatment of non-circular threads[J]. Journal of the Textile Institute Transactions, 1958, 49(1): 44-48.
[11] SHANAHAN W J, HEARLE J W S. An energy method for calculations in fabric mechanics: part II: examples of application of the method to woven fabrics[J]. Journal of the Textile Institute, 1978, 69(4): 92-100.
[12] GONG R H, OZGEN B, SOLEIMANI M. Modeling of yarn cross-section in plain woven fabric[J]. Textile Research Journal, 2009, 79(11): 1014-1020.
[13] OZGEN B, GONG R H. Modelling of yarn flattening in woven fabrics[J]. Textile Research Journal, 2011, 81(15): 1523-1531.
[14] HIRAI T, FUKAI S, SENBA T. Yarn tensile property for analysis: finite element analysis on the biaxial tensile properties of woven fabrics(part 2)[J]. Journal of the Textile Machinery Society of Japan Transactions, 1982, 35: 79-86.
[15] HIRAI T, SENBA T, IBARAKI N. Application to design of woven fabrics: finite element analysis on the biaxial tensile properties of woven fabrics(part 3)[J]. Journal of the Textile Machinery Society of Japan Transactions, 1982, 35: 87-96.
[16] LIN H, SHERBURN M, CROOKSTON J, et al. Finite element modelling of fabric compression[J]. Model-ling & Simulation in Materials Science & Engineering, 2008, 16(3):697-704.
Modeling and experimental study on yarn′s cross-section compression deformation
LI Guanzhi1,2, ZHAO Qiang1,2, WANG Jun1,3, GONG Hugh4
(1.CollegeofTextiles,DonghuaUniversity,Shanghai201620,China; 2.ChinaTextileAcademy,Beijing100025,China; 3.KeyLaboratoryofTextileScience&Technology,MinistryofEducation,Shanghai201620,China; 4.SchoolofMaterials,UniversityofManchester,ManchesterM60 1QD,UK)
In order to overcome drawbacks of the conventional yarn evenness tester in predicting fabric appearance quality, this paper presents the characterization of the individual yarn deformation and its influence on the resulting quality of the fabric appearance. In the model, the yarn deformation parameters such as the cross-sectional area, the yarn cross-sectional perimeter, the void ratio, the yarn flattening ratio f and yarn density were evaluated. Using mathematical modeling, the cross-sectional area and perimeter were presumed as the critical yarn cross-sectional parameters for predicting the fabric appearance quality. Then the finite element modeling (FEM) method and experiment verification were performed to analyze the variation of the cross-sectional area and perimeter in the process of weaving. The results show that the cross-sectional area varhes almost 2 to 3 times greater than the cross-sectional perimeter. The correlation analysis among the major ellipse radius, the cross-sectional perimeter, and the cross-sectional area are further conducted. The findings reveal a weak correlation between major ellipse radius and cross-sectional perimeter, while major ellipse radius and cross-sectional area are uncorrelated.
yarn evenness; yarn flattening ratio; finite element analysis; image processing
10.13475/j.fzxb.20161004207
2016-10-17
2016-11-11
东华大学博士生创新基金项目(CUSF-DH-D-2015014)
李冠志 (1987—),男,博士生。研究方向为纱线条干均匀度测试及布面质量预测。汪军,通信作者,E-mail: junwang@dhu.edu.cn。
TS 101.9
A
