数形结合：聚焦核心，突破难点

陈秀娟

[摘要]数形结合，即聚焦数学核心知识，通过数与形之间的对应与转化，变抽象为直观，帮助学生观察与思考，达到“以数解形”或“以形解数”的目的，以此打通学生的数学思维障碍，突破难点，构建高效的数学课堂。

[关键词]数形结合 聚焦核心 突破难点

[中图分类号]G623.5 [文献标识码]A [文章编号]2095-3089（2017）12-0058-02

数形结合，即聚焦数学核心知识，通过数与形之间的对应与转化，变抽象为直观，突破难点，构建高效课堂。教学中，如何地帮助学生“以数解形”或“以形解数”呢？下面笔者结合教学实践从三个方面加以阐述。

一、数形结合，导出概念核心

1.直观表征，建构概念模型

[案例1]三年级上册“倍的认识”

师：同学们，3月12日是植树节，六（2）班同学去植树，种了3棵杨桃树，种的荔枝树是杨桃树的4倍，荔枝树种了多少棵？

生：12棵。

师：都认为是12棵吗？这12棵是怎么来的？大家能不能用画一画、圈一圈来阐述道理？

学生一听，纷纷动笔，各抒己见。

生1：我是这样画的：3棵杨桃树用3个小圆圈表示，荔枝树是杨桃树的4倍，荔枝树就是4個3大圈。

师：为什么要3个3个地圈？

生1：因为荔枝树是和杨桃树比的。杨桃树是3棵，荔枝树是杨桃树的4倍，4个3就是12棵。

生2：老师，我是这样想的：杨桃树有3棵，我就画3小格，荔枝树有12棵，12是由4个3得来的。因为题目说荔枝树是杨桃树的4倍，就画4个3格，共12小格。

师：刚才同学们画的图中可以看出，有的画圆圈，有的画小格。尽管画法不同，但是它们都有一个共同的特点，谁来说一说？

生3：我发现尽管他们画的方式不同，但呈现的都是杨桃树3棵，荔枝树的棵树就是龙眼树的4倍，12棵。

师：对了！都表示“荔枝树的棵树就是杨桃树的4倍”，你的发现就是今天我们要研究的内容，这节课我们一起来探究“倍”！（揭示课题）

教学“倍的认识”，笔者有意让学生画一画、圈一圈、说一说，灵活运用数形结合的思想培养学生的思考能力和表达能力，帮助学生直观表征“倍”的认识一一“倍”是表示两个量的比较关系，学生对建构“倍”的概念模型，既简洁生动，又准确深刻。

2.图文并茂，凸显概念本质

教学长方形的周长意义后，笔者设计一组练习，引导学生采用对比的思维，加深理解长方形的周长，凸显其概念本质。

（1）出示一个长6分米，宽3分米的长方形（图形1），求这个长方形的周长。

（2）在图1的右上角剪去一个长2分米，宽1分米的小长方形（图2）。求这个“台阶形”的周长。

（3）比较这两个图形，说说你的发现。

（4）质疑反馈：图2剪去一个小长方形后，为什么周长与图1还是相同？

以上这组练习以图形的比较形式出现，重在抓住概念的核心本质，引导学生直观分析、比较，加深学生对周长的理解，使得学生的思维更加精细化。这道题其实也是让学生经历周长与面积的辨析，加深对长方形的周长的深度认知，为后续学习长方形的面积计算埋下伏笔。

二、数形结合，触摸计算核心

1.以形解数，培养数感

对较小的数的认识，一般通过数实物来培养孩子们的数感，但是学了1000以内数的认识后，如果较大数目的数的认识，还停留在数实物，不利于数感的培养。对于中低年级的孩子，数感的培养要基于一定的策略依托，可以借助线段图估一估，“以形解数”客观感知1000以内数的大小，帮助学生形成良好的数感意识。

[案例2]教学“1000以内数的认识”

师：刚才大家学会了数数，现在我们来看这一条线段，其中一小段是200，那么这条线段是多少？谁来估一估？

生：大约600！

师：为什么，说说你是怎么估的？

生1：整条线段，我刚才比划了一下，可以分成大致相等的3小段，因为每小段是200，所以估出来大约200是600。

师：你的表述非常到位，老师很佩服你！如果还是这条线段，只改变它的数据和问题估一估，现在每小段大约是多少？

生2：我估算约300。跟上面那题一样，大概可以分成相等的3小段，因为整段是900，所以每小段估出来大约是300。

师：看来同样的一条线段，因为数据不同，标准不一样，估出来的数也不一样！

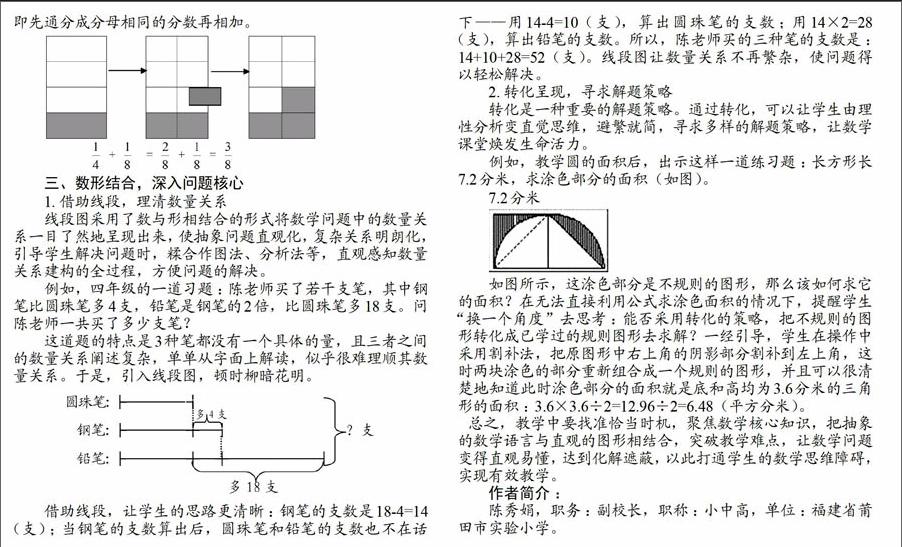
2.直观图示，阐明算理即先通分成分母相同的分数再相加。

三、数形结合，深入问题核心

1.借助线段，理清数量关系

线段图采用了数与形相结合的形式将数学问题中的数量关系一目了然地呈现出来，使抽象问题直观化，复杂关系明朗化，引导学生解决问题时，糅合作图法、分析法等，直观感知数量关系建构的全过程，方便问题的解决。

例如，四年级的一道习题：陈老师买了若干支笔，其中钢笔比圆珠笔多4支，铅笔是钢笔的2倍，比圆珠笔多18支。问陈老师一共买了多少支笔？

这道题的特点是3种笔都没有一个具体的量，且三者之间的数量关系阐述复杂，单单从字面上解读，似乎很难理顺其数量关系。于是，引入线段图，顿时柳暗花明。

借助线段，让学生的思路更清晰：钢笔的支数是18-4=14（支）；当钢笔的支数算出后，圆珠笔和铅笔的支数也不在话下——用14-4=10（支），算出圆珠笔的支数；用14×2=28（支），算出铅笔的支数。所以，陈老师买的三种笔的支数是：14+10+28=52（支）。线段图让数量关系不再繁杂，使问题得以轻松解决。

2.转化呈现，寻求解题策略

转化是一种重要的解题策略。通过转化，可以让学生由理性分析变直觉思维，避繁就简，寻求多样的解题策略，让数学课堂焕发生命活力。

例如，教学圆的面积后，出示这样一道练习题：长方形长7.2分米，求涂色部分的面积（如图）。

如图所示，这涂色部分是不规则的图形，那么该如何求它的面积？在无法直接利用公式求涂色面积的情况下，提醒学生“换一个角度”去思考：能否采用转化的策略，把不规则的图形转化成已学过的规则图形去求解？一经引导，学生在操作中采用割补法，把原图形中右上角的阴影部分割补到左上角，这时两块涂色的部分重新组合成一个规则的图形，并且可以很清楚地知道此时涂色部分的面积就是底和高均为3.6分米的三角形的面积：3.6×3.6÷2=12.96÷2=6.48（平方分米）。总之，教学中要找准恰当时机，聚焦数学核心知识，把抽象的数学语言与直观的图形相结合，突破教学难点，让数学问题变得直观易懂，达到化解遮蔽，以此打通学生的数学思维障碍，实现有效教学。