基于多传感器的神经网络和D-S证据理论在故障诊断中的应用

周国宪， 伍 星， 刘 韬

(昆明理工大学 机电工程学院， 云南 昆明 650500)

基于多传感器的神经网络和D-S证据理论在故障诊断中的应用

周国宪， 伍 星， 刘 韬

(昆明理工大学 机电工程学院， 云南 昆明 650500)

为提高滚动轴承故障诊断的准确性， 本文提出了一种基于多传感器神经网络和D-S证据理论的故障诊断方法， 并通过包含3个传感器的监测数据融合对模型进行了验证. 首先， 利用两个加速度传感器和一个声传感器采集滚动轴承的振动信号和噪声信号. 其次， 分别对两个加速度传感器的振动信号进行总体经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)得到各固有模态函数(Intrinsic Mode Function, IMF)分量， 并提取各IMF分量的能量特征作为子网络1和子网络2的输入参数； 同时， 对声传感器的噪声信号进行小波包分解提取各频段能量特征作为子网络3的输入参数； 3个子网络的局部诊断结果归一化处理得到各自独立的证据体， 对冲突证据加权修正并运用D-S证据理论进行决策级的信息融合得出最终的故障诊断结果. 实验结果表明： 该方法可有效提高滚动轴承故障诊断的准确率， 降低故障诊断的不确定性.

多传感器； D-S证据理论； 滚动轴承； 故障诊断； 信息融合

0 引 言

证据理论作为一种非确定性推理算法[1]， 能有效综合来自不同传感器的信息， 是一种重要的决策级信息融合方法， 在表示和处理不确定问题时具有明显的优势. 但证据理论应用于故障诊断领域， 其关键问题在于如何确定辨识框架中各命题的基本信度分配(Basic Probability Assignment， 简称BPA). 在传统的证据理论中， 基本信度分配需要相关领域专家的经验和知识给出， 具有一定的主观性.

为解决此问题， 很多学者都提出了自己的解决方法. 周皓[2]等利用SVM精度下限对Platt概率模型进行加权处理获取BPA； 苏思[3]等引用统计理论中的马氏距离计算各证据与其余证据组合的距离， 导出各证据的重要性权系数， 由此对证据的BPA进行转换； 李巍华[4]等通过计算证据体间的欧式距离获得证据的可信度因子， 据此对原始证据进行修正， 从而获得修正后的BPA， 并应用于变速箱的齿轮故障诊断； 冯爱伟[5]等将神经网络与证据理论融合， 实现对煤矿通风机的故障诊断； 张雷[6]等利用SVM构造分类器， 对多个分类器的结果使用D-S证据进行合成， 成功应用于发动机磨损故障的诊断； 徐春梅[7]等将神经网络的输出作为证据进行合成， 对涡轮机故障进行诊断； 雷蕾[8]等根据SVM基分类器对输入数据(包括分类标签、 后验概率和混淆矩阵等)的实际分类情况构造BPA； 周爱华[9]等将粗糙集理论和证据理论应用于变压器的故障诊断中； 孙伟超[10]等利用粗糙集将信息源给出的诊断数据转化为证据理论中的BPA， 实现对航空电子装备故障诊断.

鉴于此， 本文提出一种BP神经网络和D-S证据理论有机结合的故障诊断方法， 并应用于滚动轴承的故障诊断. 该方法充分利用了多传感器的互补冗余信息和D-S证据理论处理不确定信息能力， 在QPZZ- II旋转机械故障模拟试验台进行4类(正常、 外圈故障、 内圈故障及滚动体故障)滚动轴承的故障模拟实验验证了该方法的有效性.

1 D-S证据理论

1.1 证据理论基本概念

1.1.1 辨识框架

在证据理论中， 通常用有限集合来代表命题， 假设Θ是一个有限集合且元素互斥， 那么称该集合称为辨识框架. 辨识框架表示某一事件的所有可能.

1.1.2 基本信度分配函数

在辨识框架Θ中， 基本信度分配函数m是一个从集合2θ到[0,1]的映射，A表示辨识框架Θ的任意一个子集， 记A⊆Θ， 且满足

则称m为辨识框架Θ上的基本信度分配函数.m(A)表示事件A的基本信度分配函数， 其含义为对证据A的信任程度.

1.1.3 信度函数

信度函数Bel是一个集合2θ到[0,1]的映射， 假设A表示识别Θ中的任一子集， 记A⊆Θ， 且满足

则把Bel(A)称做A的信度函数， 表示证据A为真命题时的信度程度.

1.2 Dempster组合规则

假设在同一框架Θ下，m1,m2,…,mn是n个独立证据源的基本信度分配函数， 焦元分别为Ai(i=1,2,…,N)， 那么多个证据源的D-S合成规则为

式中：Cf为冲突系数， 表示各个证据间的冲突大小.

2 BP神经网络理论

2.1 BP神经网络模型

反向传播网络(Back Propagation， 简称BP网络)是目前应用最广泛的神经网络模型之一[11]， 其拓扑结构包括输入层(Input layer)、 隐含层(Hidden layer)和输出层(Output layer). 在前向传递中， 输入信号从输入层经隐含层逐层处理， 直至输出层， 如果输出层得不到期望输出， 则转入反向传播， 并根据预测误差调整网络权值和阈值， 从而使BP神经网络预测输出不断逼近期望输出.

2.2 BP神经网络数学形式

设输入层、 隐含层和输出层神经元之间的连接权值分别为ωij,ωjk， 隐含层阈值及输出层阈值分别为a,b. 根据输入向量X， 输入层和隐含层间连接权值ωij以及隐含层阈值a， 可计算隐含层输出H.

式中：j=1,2,…,l,f为隐含层的激活函数.

再根据隐含层输出H， 与输出层的连接权值ωjk和阈值b， 可计算BP神经网络预测输出O

式中：k=1,2,…,m.

再由网络预测输出和期望输出即可计算网络的预测误差e.

式中：k=1,2,…,m.

3 信息融合的故障诊断

本文提出的基于BP神经网络和D-S证据理论的多传感器信息融合的滚动轴承故障诊断方法框图如图 1 所示.

图 1 基于神经网络的证据理论诊断框图Fig.1 The diagnosis diagram based on neural network and evidence theory

根据滚动轴承的4种不同状态， 设辨识框架={正常A1， 内圈故障A2， 外圈故障A3， 滚动体故障A4}.

在证据融合之前需要判断证据间是否存在冲突， 若存在冲突可按照文献[13]提出的方法对冲突证据进行改进的证据组合[12]， 否则按照Dempster组合规则进行融合. 融合处理流程如图 2 所示.

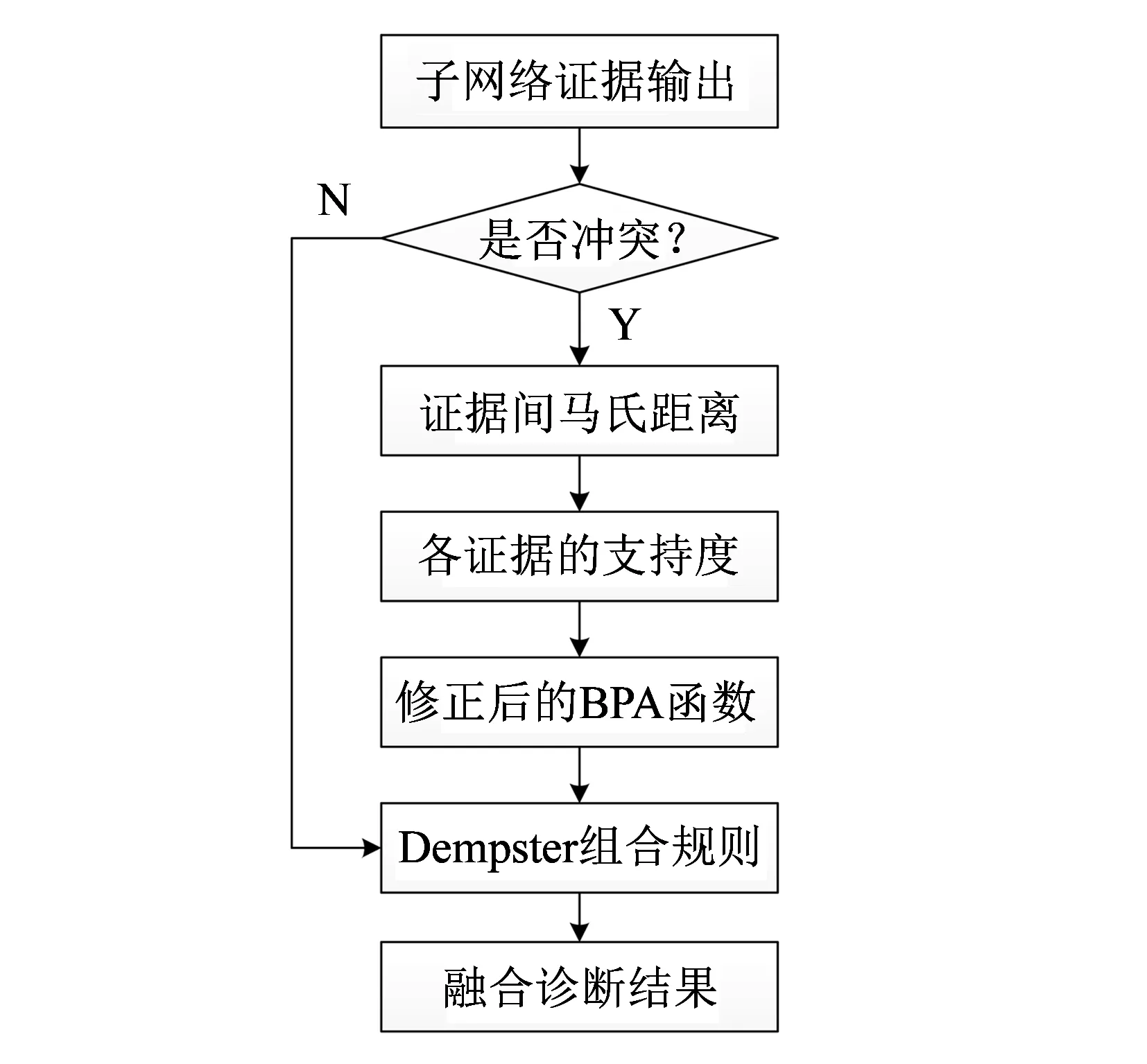
图 2 基于证据理论的融合处理流程Fig.2 Fusion process based on the evidence theory

3.1 BP神经网络的局部诊断

为了验证算法的有效性， 本文以圆柱滚子轴承N205EM为研究对象， 采用EX603C01型加速度传感器和声望公司生产的MPA416型传声器分别采集滚动轴承4种不同状态下的振动信号和噪声信号. 试验中， 轴承转速900 r/min， 采样频率25.6 kHz， 每种状态采集5组数据， 每组数据采样点数512 000. 随机选取其中3组作为神经网络的训练集， 余下的2组作为测试集. 具体的传感器安装位置如图 3 所示.

图 3 传感器安装的位置及典型故障Fig.3 Installation location of the sensors and typicl fault

3.1.1 故障特征的提取

1) 振动信号的故障特征提取

根据振动信号非平稳性的特点[13-14]， 选取常用的8个时域统计量特征参数(包括有效值， 峰峰值， 歪度， 峭度， 峰值指标， 裕度指标， 脉冲指标和波形指标)和EEMD分解得到的前8个IMF分量的能量特征作为特征参数空间1. 图 4 为滚动轴承4种不同状态下随机抽取5 120个采样点EEMD分解后的前8个IMF能量分布情况.

从图 4 中可以容易地看出滚动轴承的正常状态IMF能量主要集中在第6和第7个IMF， 而故障信号主要集中在前3个IMF， 即正常信号的能量主要集中在低频段， 故障信号的能量主要集中在中高频段. 除此之外， 3类典型故障信号的IMF能量分布也不相同， 可以作为故障分类的特征向量.

图 4 滚动轴承4种不同状态的前8个IMF能量分布Fig.4 Rolling bearing four states of first eight IMF energy distribution

2) 噪声信号的故障特征提取

利用小波包分析可得到噪声信号分解低频和高频的特点[15-16]， 本文对采集的噪声信号利用小波包wpdencmp函数进行降噪， 然后进行小波包基函数为coif5的3层小波包分解得到8个频段， 提取各频段能量特征作为特征参数空间2. 噪声信号4种不同状态下小波包分解系数如图 5 所示.

3.1.2 神经网络模型的构建

BP神经网络的构建根据输入输出数据特点确定. 对于BP子网络1、 BP子网络2特征参数空间维数为16， BP子网络3的特征参数空间维数为8， 待识别的状态共4类. 根据文献[18]隐含层节点数选取方法[17]， BP子网络1、 BP子网络2 的网络模型为16×33×4， 即输入层节点数、 隐含层节点数及输出层节点数分别为16, 33和4； BP子网络3的网络模型为8×17×4， 即输入层节点数、 隐含层节点数及输出层节点数分别为8, 17和4. 采用附加动量和变学习率的方法改进BP算法， 设定最大学习率为0.2， 最小学习率为0.01， 期望误差0.05. 设网络的期望输出={正常[1000]、 外圈故障[0100]、 内圈故障[0010]、 滚动体故障[0001]}. BP网络的局部诊断结果如表 1 所示.

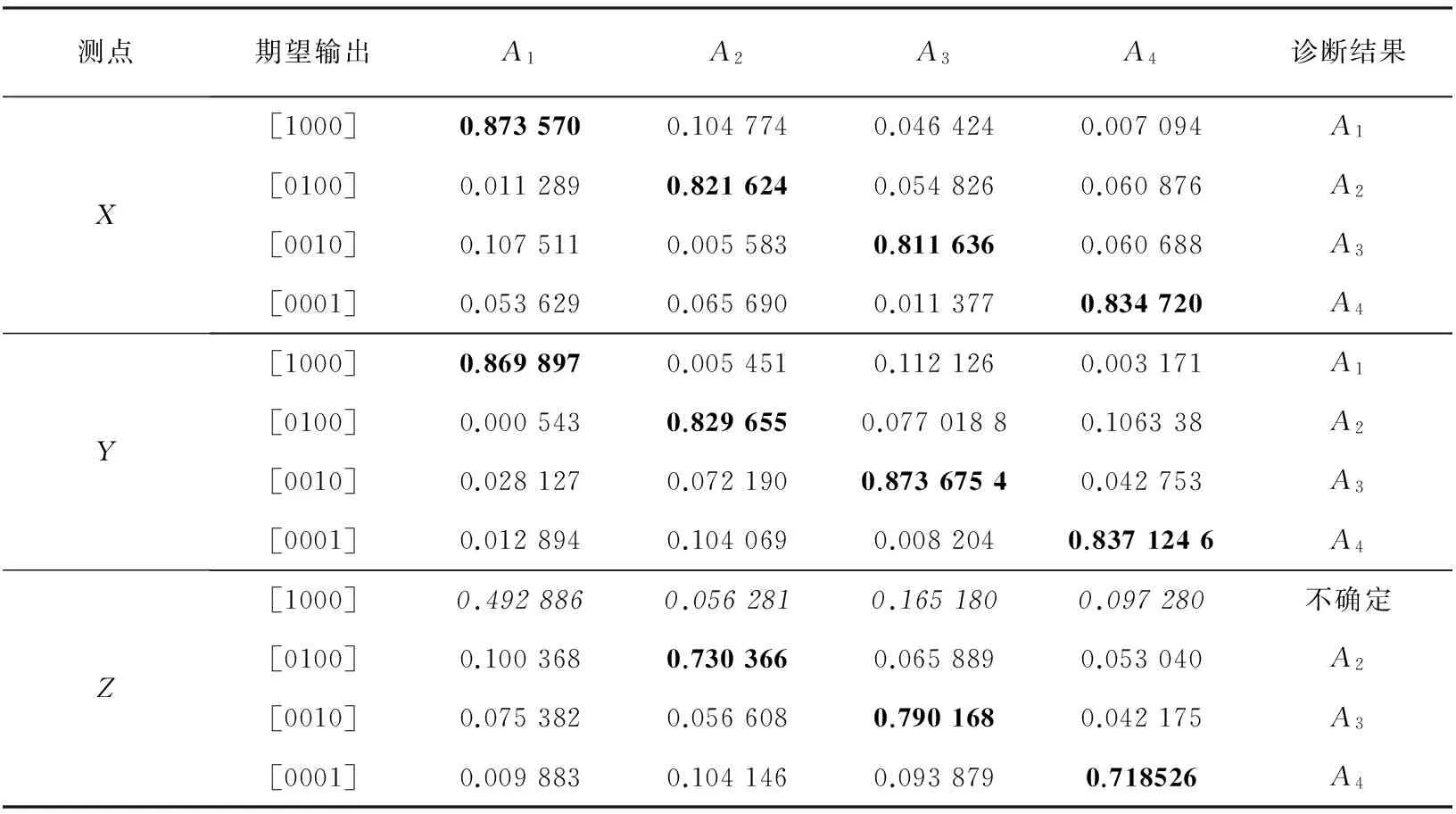
表 1 BP神经网络的局部诊断结果

从表 1 中可以看出测点Z的第1类故障局部诊断准确度不高， 不能得到正确的诊断结果， 由此可认为证据体间存在冲突， 因而该证据体的基本信度分配按照文献[13]的组合规则进行修正.

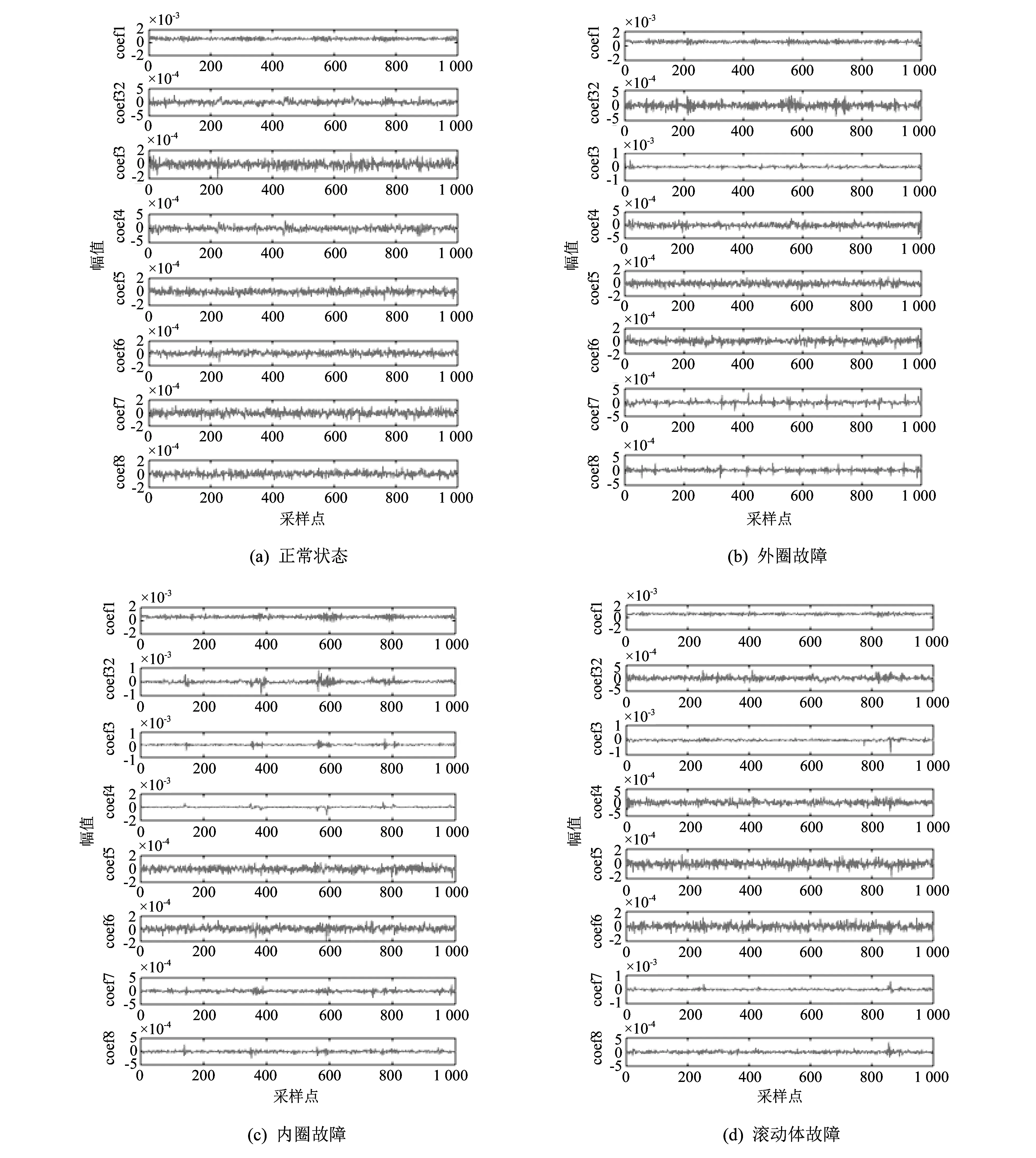
图 5 滚动轴承4种不同状态3层小波包分解系数Fig.5 Rolling bearing four states of three layer wavelet packet decomposition coefficient

3.2 基于D-S证据理论的融合诊断

设第i个网络的第j个输出值为Mi(j)， 则该网络对判断j的基本信度分配为

式中：mi(j)表示第i个网络对判断j的基本信度分配；k表示第i个网络的输出个数；ek表示网络的预测误差；m(θ)表示网络诊断的不确定性. 神经网络诊断结果归一化后的基本信度分配如表 2 所示.

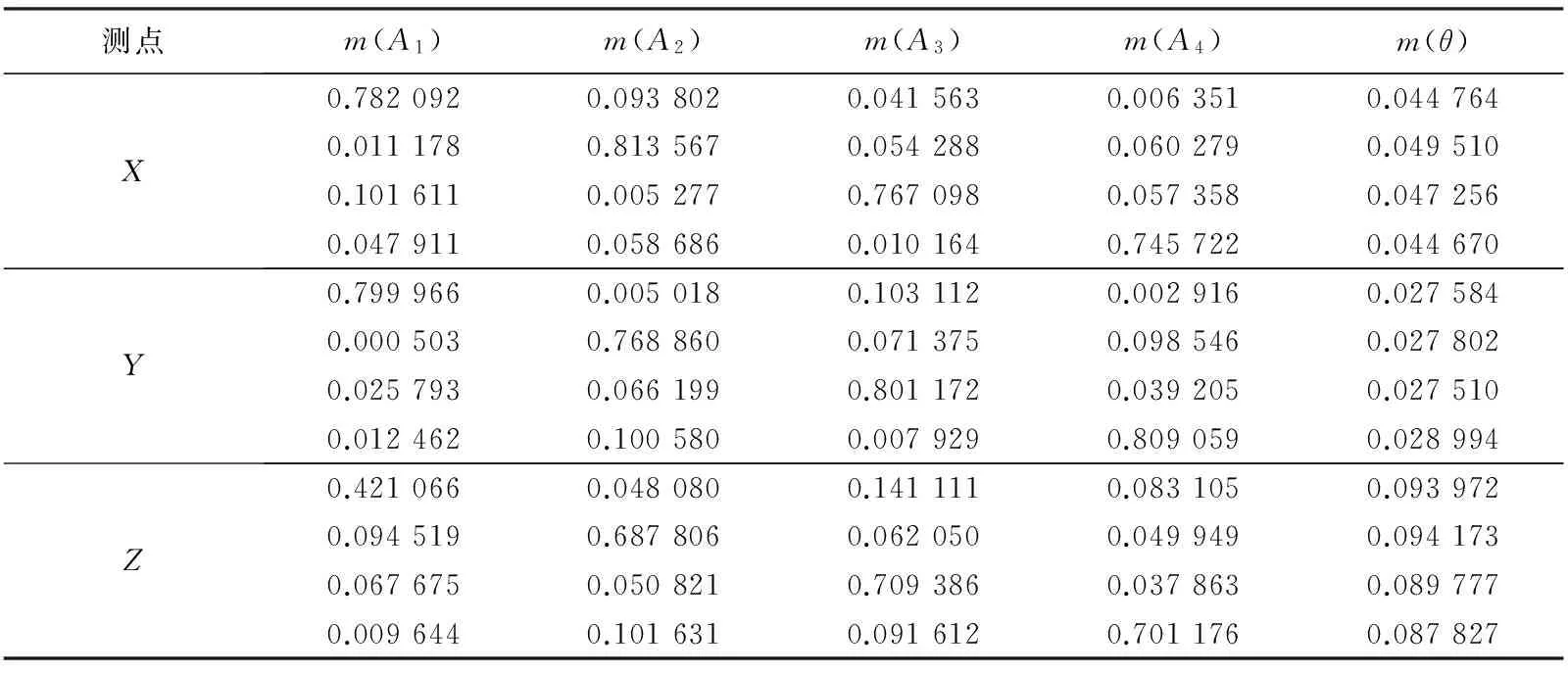
表 2 BP神经网络的基本信度分配

根据表 2 神经网络的基本信度分配， 采用Dempster组合规则进行融合并基于基本概率赋值的决策法[18-19]， 得到网络输出的融合诊断结果如表 3 所示.

融合诊断结果可以看出， 采用神经网络与D-S证据理论的信息融合故障诊断方法均可得到正确的诊断结果， 特别是进行多个测点的信息融合诊断时， 诊断正确率和不确定性达到极值， 也就是说多个传感器信息融合可充分利用传感器间的冗余和互补信息， 有效提高故障诊断的可信度.

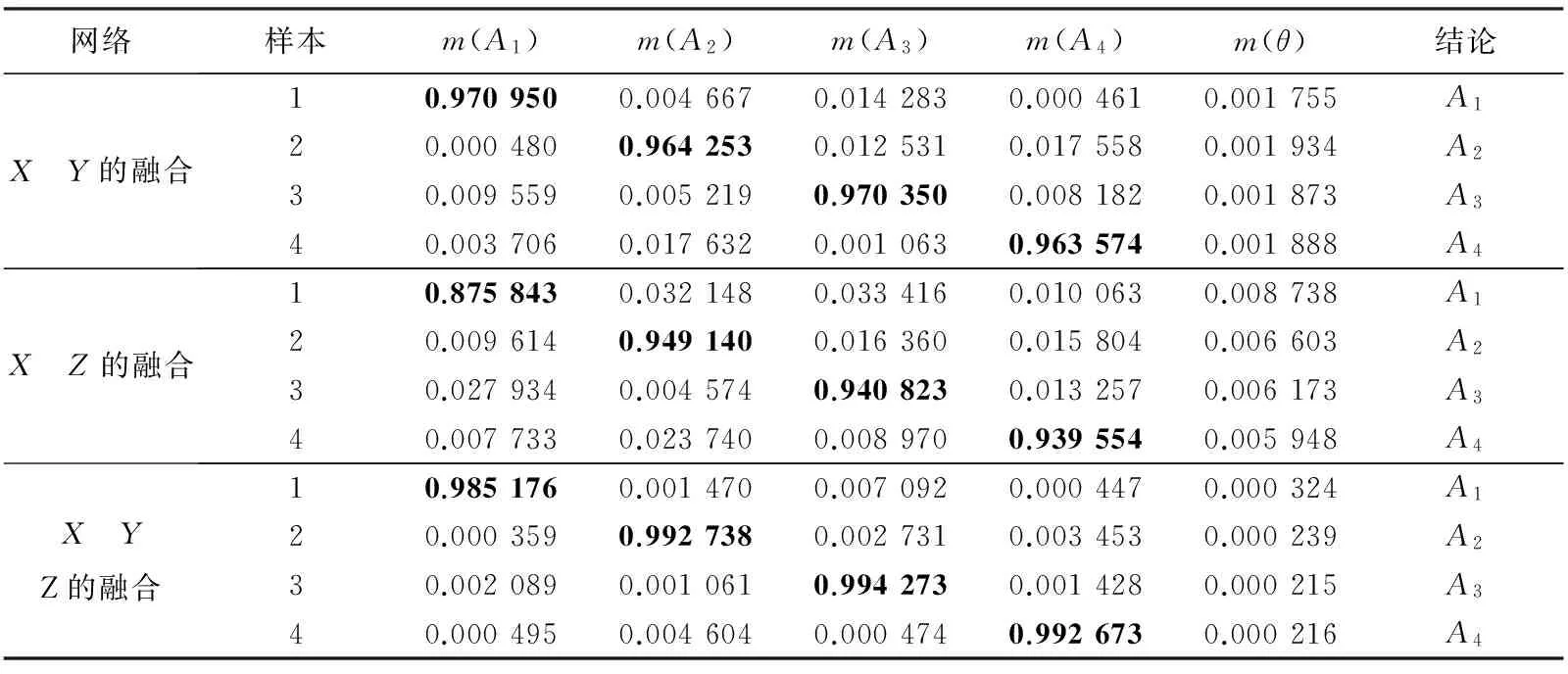
表 3 D-S证据理论融合诊断结果

4 结 论

本文提出一种基于多传感器的神经网络和D-S证据理论的滚动轴承故障诊断方法， 采用3个神经网络分别对3个不同测点的振动信号和噪声信号进行局部诊断并进行归一化处理， 获取各个独立的证据体， 通过对冲突证据修正后进行证据理论的决策级融合诊断， 从而实现神经网络和证据理论有机结合. 实验结果表明： 该方法可有效提高滚动轴承故障诊断的识别率， 降低故障诊断过程的不确定性， 在故障诊断等相关领域具有一定的应用价值.

[1] 韩崇昭， 朱洪艳. 多源信息融合[M]. 北京： 清华大学出版社， 2010.

[2] 周皓， 李少洪. 支持向量机与证据理论在信息融合中的结合[J]. 传感技术学报， 2008， 21(9)： 1566-1570. Zhou Hao， Li Shaohong. Combination of support vector machine and evidence theory in information fusion[J]. Chinese Journal of Sensors and Actuators， 2008， 21(9)： 1566-1570. (in Chinese)

[3] 苏思， 姜礼平， 邹明. 基于多分类支持向量机和证据合成方法的多传感器信息融合研究[J]. 兵工自动化， 2010， 29(1)： 59-62. Su Si， Jiang Liping， Zou Ming. Research of multi-sensor information fusion based on multi-class classification SVM and improved evidence combination method[J]. Ordnance Industry Automation， 2010， 29(1)： 59-62. (in Chinese)

[4] 李巍华， 张盛刚. 基于改进证据理论及多神经网络融合的故障分类[J]. 机械工程学报， 2010， 46(9)： 93-99. Li Weihua， Zhang Shenggang. Fault classification based on improved evidence theory and multiple neural network fusion[J]. Journal of Mechanical Engineering, 2010， 46(9)： 93-99. (in Chinese)

[5] 冯爱伟. 基于神经网络与证据理论的煤矿通风机故障诊断[J]. 煤矿机械， 2010， 31(6)： 249-251. Feng Aiwei. Coal mine ventilation motor fault diagnosis based on neural network and evidence theory[J]. Coal Mine Machinery， 2010， 31(6)： 249-251. (in Chinese)

[6] Zhang Lei， Dong Yanfei. Research on diagnosis of AC engine wear fault based on support vector machine and information fusion[J]. Journal of Computers， 2012， 7(9)： 2292-2297.

[7] Xu Chunmei， Zhang Hao， Peng Daogang et al. Study of Fault Diagnosis of Integrate of D-S Evidence Theory Based on Neural Network for Turbine[J]. Energy Procedia， 2012， 16： 2027-2032.

[8] 雷蕾， 王晓丹. 结合SVM与DS证据理论的信息融合分类方法[J]. 计算机工程与应用， 2013， 49(11)： 114-117. Lei Lei， Wang Xiaodan. Approach of information fusion and classification by SVM and DS evidence theory[J]. ComputerEngineering and Applications， 2013， 49(11)： 114-117. (in Chinese)

[9] Zhou AiHua， Yao Yi， Song Hong. Power transformer fault diagnosis based on integrated of rough set theory and evidence theory[C]. International Conference on Intelligent System Design & Engineering Applications， 2013： 1049-1052.

[10] 孙伟超， 李文海， 李文峰. 融合粗糙集与D-S证据理论的航空装备故障诊断[J]. 北京航空航天大学学报， 2015， 41(10)： 1902-1909. Sun Weichao， Li Wenhai， Li Wenfeng. Avionic devices fault diagnosis based on fusion method of rough set and D-S theory[J]. Journal of Beijing University of Aeronautics and Astronautics， 2015， 41(10)： 1902-1909. (in Chinese)

[11] 何正嘉， 陈进， 王太勇， 等. 机械故障诊断理论及应用[M]. 北京： 高等教育出版社， 2010.

[12] 鲁睿， 徐启建， 张杰， 等. 一种基于马氏距离的冲突证据组合方法[J]. 通信技术， 2015(3)： 278-282. Lu Rui， Xu Qijian， Zhang Jie， et al. Combination method of conflicting evidence based on mahalanobis distance[J]. Communications Technology， 2015(3)： 278-282. (in Chinese)

[13] 李敏， 傅攀. EMD和Elman神经网络在滚动轴承故障诊断中的应用[J]. 四川兵工学报， 2011， 32(8)： 59-62. Li Min， Fu Pan. The EMD and Elman neural network application in the rolling bearing fault diagnosis[J]. Sichuan Armamentarii， 2011， 32(8)： 59-62. (in Chinese)

[14] 于婷婷. 基于BP神经网络的滚动轴承故障诊断方法[D]. 大连： 大连理工大学， 2008.

[15] 李新欣. 船舶及鲸类声信号特征提取和分类识别研究[D]. 哈尔滨： 哈尔滨工程大学， 2012.

[16] 肖顺根， 宋萌萌. 基于小波包能量神经网络的滚动轴承故障诊断方法[J]. 机械强度， 2014， 36(3)： 340-346. Xiao Shungen， Song Mengmeng. Fault diagnosis of roller bearing based on wavelet packet energy neural network[J]. Journal of Mechanical Strength， 2014， 36(3)： 340-346. (in Chinese)

[17] Sun Weixiang， Chen Jin， Li Jiaqing. Decision tree and PCA-based fault diagnosis of rotating machinery[J]. Mechanical Systems & Signal Processing， 2007， 21(3)： 1300-1317.

[18] Ouyang Ning， Liu Zhao， Kang Yankang. A method of distributed decision fusion based on SVM and D-S evidence theory[C]. 5th International Conference on Visual Information Engineering (VIE 2008)， 2008： 261-264.

[19] 华云鹏. 基于多源信息融合技术的船舶电力推进系统故障诊断研究[D]. 大连： 大连海事大学， 2012.

Multi-Sensor Application in Fault Diagnosis Based on Neural Network and D-S Evidence Theory

ZHOU Guoxian， WU Xing， LIU Tao

(Faculty of Mechanical & Electrical Engineering， Kunming University of Science and Technology， Kunming 650500， China)

To improve the accuracy of rolling bearing fault diagnosis，this paper puts forward a multi-sensor fault diagnosis method based on neural network and D-S evidence theory，and test the validity of model with three sensors monitoring data. First，two acceleration sensors and a acoustic sensor are used to collect vibration signals and noise signals of rolling bearing. Then，by using Ensemble Empirical Mode Decomposition(EEMD) decompose the vibration signals of two acceleration sensors and get each Intrinsic Mode function(IMF) component，the energy characteristics of each IMF component was extracted as the input vector of thesubnet 1 and subnet 2 respectively；meanwhile using WP(wavelet packet) extract noise signals energy spectrum feature and the result was taken as the input parameters of the subnet3；Finally，The local diagnostic results of three sub-networks are normalized processing and obtained each independent evidence，applying weighted correction method adjuste the conflict evidences and obtain the final fault diagnostic results by using D-S evidence theory to fuse the information of each evidence. The experimental results show that the method can effectively enhance the accuracy and reduce the uncertainty in rolling bearing fault diagnosis.

multi-sensor； D-S evidence theory； rolling bearing； fault diagnosis； information fusion

2016-12-22

国家自然科学基金资助项目(51465022)

周国宪(1993-)， 男， 硕士生， 主要从事机电系统故障诊断等研究.

1671-7449(2017)04-0290-08

TP206+.3

A

10.3969/j.issn.1671-7449.2017.04.003