十水草酸镧的热分解及其动力学分析

邓庚凤，姬传红，谢 耀，谭 敏，蔡晨龙，王 赟，曾青云

(江西理工大学冶金与化学工程学院，江西赣州341000)

十水草酸镧的热分解及其动力学分析

邓庚凤，姬传红，谢 耀，谭 敏，蔡晨龙，王 赟，曾青云

(江西理工大学冶金与化学工程学院，江西赣州341000)

用热重-差热(TG-DTA)技术，在不同升温速率条件下，研究了十水草酸镧在空气气氛下的热分解过程.分别采用Ozawa-Flynm-Wall法、Kissinger法、Crane法和同步热分析法确定其热分解动力学参数.TG-DTA曲线表明：十水草酸镧分解为四个阶段，前两个阶段为脱水过程，后两个阶段为La2(C2O4)3的分解过程.实验计算得出四步反应表观活化能E分别为83.92、76.04、136.26、162.61 kJ·mol-1左右；指前因子A分别为4.92×1010、6.1×107、2.1×109、8.46×106s-1左右；反应级数n均为1左右, 并用Coats-Redfem积分法得出第三步分解机理受F1控制.

G-DTA；La2(C2O4)3·10H2O；热分解；动力学参数

稀土是我国的战略性资源[1]，稀土氧化物因其优异性能，被广泛应用于荧光材料，永磁材料，催化材料，功能陶瓷材料，储氢材料等各个行业[2].稀土草酸盐具有沉淀物晶型好，易于过滤分解等优点，因此它是制备多数稀土氧化物、氟化物等稀土化合物的前驱体，尤其是制备具有可控粒度的稀土氧化物常用的前驱体.稀土氧化物的粒度、形貌、性能受其前驱体的热分解过程影响很大，特别是制作纳米级氧化稀土更需要控制一定的热分解条件[3].因为材料的组织形貌和粒度受制备过程的影响极大，在沉淀条件下形成的前驱体微粒，在热分解时会有所变化[4].有关固态物质的热分解动力学研究，目前主要方法为热分析法[5].通过研究稀土草酸盐的热分解化学反应过程，用热分析法掌握其分解过程的规律和控制产物的组织形貌和粒度是十分重要的[6].

热分析方法用于稀土草酸盐热分解过程及动力学研究的实例较多，方正东等[7]研究了十水草酸铈的热分解步骤和动力学参数；胡艳红等[8]研究了大颗粒草酸铈的热分解步骤和动力学参数；黄昕等[9]研究了草酸钕的热分解过程和中间产物生成的机理函数；张克立等[10]曾对十水草酸镧做了热分解分析确定了其分解步骤，但是没有草酸镧在不同升温速率下热分解过程和动力学参数的研究计算.

本实验拟用热重-差热分析法(TG-DTA[11])研究十水草酸镧(La2(C2O4)3·10H2O)在程序升温下的热分解行为，通过采集不同升温速率下La2(C2O4)3·10H2O热分解的TG-DTA数据，分别利用Ozawa-Flynm-Wall[12]法、Kissinger[13]法、Crane[14]法和同步热分析法[15]对La2(C2O4)3·10H2O进行热分解和动力学分析，并用Coats-Redfem[16]积分法进行确认反应机理函数，从而确定各步分解反应级数、活化能和反应机理，为La2(C2O4)3·10H2O分解制备良好形貌和合适粒度的稀土氧化物提供一定的理论依据.

1 实 验

1.1 实验方法

实验所用仪器为DTU-3B微机差热同步热分析仪，技术指标：升温范围：20～1 450 ℃；灵敏度：1 μg；升温速率：0.1～40 ℃/min；参比物：分析纯Al2O3；试验样品为：99.9%的La2(C2O4)3·10H2O.采用5、10、15、20、25 K·min-1的五组升温速率分别加热分解La2(C2O4)3·10H2O，获得其在空气下热分解过程的TG-DTA曲线.

1.2 数据处理方法

分别利用Ozawa-Flynm-Wall法、Kissinger法、Crane法和同步热分析法对La2(C2O4)3·10H2O进行热分解和动力学分析，并用Coats-Redfem积分法确认反应机理函数.

根据Arrhenius[17]公式，固体热分解的反应动力学方程一般为：

(1)

(2)

1.2.1 Ozawa-Flynm-Wall法

Ozawa-Flynm-Wall法是利用不同升温速率下TG曲线上相同转化率的温度T与升温速率β的关系，由式(2)转化为

(3)

在上述公式中，用logβ对1/T作图，用最小二乘法线性拟合，得到直线斜率即可求得活化能Ea.

1.2.2 Kissinger法

Kissinger法是利用各步反应在不同升温速率下DTA曲线上峰值温度Tmax和升温速率β的关系，其方程由式(2)转化得到

(4)

1.2.3 Crane法

Crane法也是利用不同升温速率下的DTA峰顶温度而计算的，但是它根据升温速率β和DTA峰顶温度Tmax的关系得出，由方程式(2)转化得：

(5)

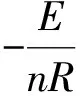
1.2.4 同步热分析法

同步热分析法是利用TG和DTA曲线，在不同升温速率下DTA曲线的峰顶温度Tmax下对应TG线上的转化率α和升温速率β的关系，由方程(2)转化为：

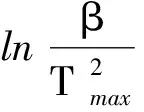
(6)

αmax为DTA曲线上峰顶温度Tmax对应TG曲线的转化率.

1.2.5 Coats-Redfem积分法

Coats-Redfem积分法是研究机理函数的常用方法，其方程为

(7)

2 结果与讨论

2.1La2(C2O4)3·10H2O热分解机理分析

为研究La2(C2O4)3·10H2O的热分解机理，选择升温速率β为10 K·min-1下 La2(C2O4)3·10H2O的热分解数据，其TG-DTA实验结果如图1所示.

图1 10K·min-1的La2(C2O4)3·10H2O热分解TG-DTA曲线 Fig.1 TG-DTA curves of lanthanum oxalate decahydrate at a heating rate of 10 K·min-1

由图1的TG曲线可以看出，TG线上有四个失重台阶，DTA图上有相应的四个吸放热峰，说明 La2(C2O4)3·10H2O的分解过程分四步进行.第一步：当温度为344.38～ 383.78 K 时，TG失重4.4%，与理论上失去2个水分子失重率应为4.7%的计算值相差约0.3%，说明此步反应为失去2个水分子；第二步：当温度385.94～ 540.92 K 时，失重21.5%，与理论上失去8个水分子失重率为19.9%的计算值相差 0.6%，说明此步反应为失去8个水分子；第三步：当温度为615.58～ 744.75 K时，失重22.4%，与理论上失去2个CO2分子和3个CO分子失重率为23.8%的计算值相差1.4%，说明此步反应放出2个CO2分子和3个CO分子；第四步：当温度为909.07～ 969.84 K 时，失重5.3%，与理论失去1个CO2失重率为6.1%的计算相差0.8%，说明此步反应放出1个CO2分子.

由此可以推断出 La2(C2O4)3·10H2O 的热分解过程分为如下四步：

La2(C2O4)3·10H2O→La2(C2O4)3·8H2O+2H2O

La2(C2O4)3·8H2O → La2(C2O4)3+8H2O

La2(C2O4)3→ La2CO5+2CO2+3CO

La2CO5→ La2O3+CO2

为进一步验证第三步分解过程的产物，实验在 700 K 下对La2(C2O4)3·10H2O进行焙烧2 h，并将焙烧产物进行XRD表征分析，结果如图2所示.

图2 700 K下十水草酸镧焙烧产物的XRD Fig.2 XRD of lanthanum oxalate decahydrate’s calcined product at 700 K

由图2的XRD结果可知，第三步的分解产物确实为La2CO5，进一步验证了 La2(C2O4)3·10H2O 在热分解的产物和理论分析一致.

2.2 La2(C2O4)3·10H2O热分解动力学分析

2.2.1 Ozawa-Flynm-Wall法热分解动力学分析

因为Ozawa-Flynm-Wall法是利用不同升温速率下TG曲线上相同转化率的温度T与升温速率β的关系进行动力学分析，实验在5、10、15、20、25 K·min-1的五组升温速率下，得到La2(C2O4)3·10H2O 在空气气氛下的热分解TG曲线如图3所示.

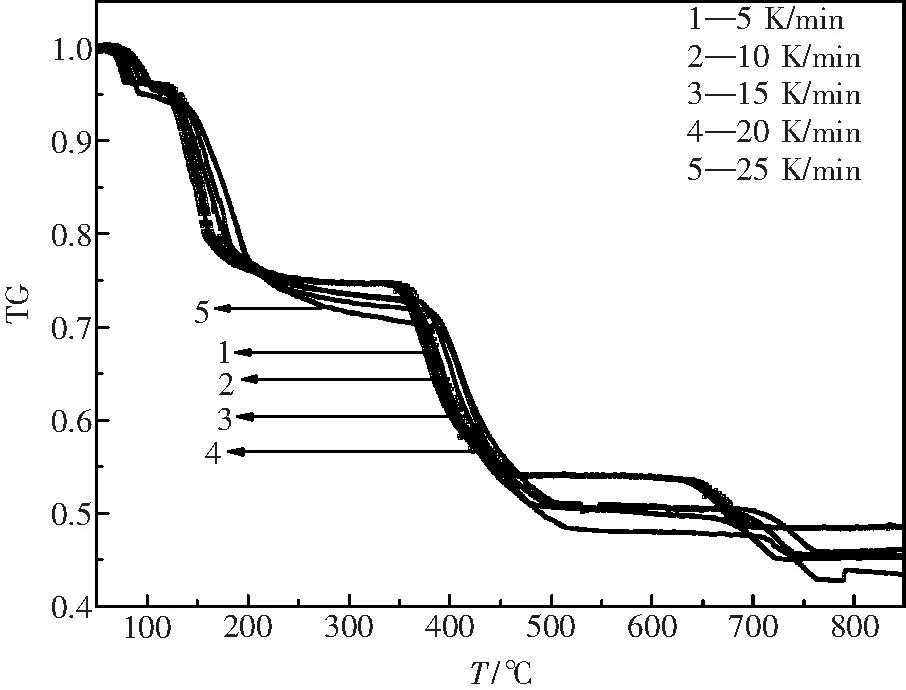
图3 不同升温速率下La2(C2O4)3·10H2O的TG-T曲线 Fig.3 TG-T curves of lanthanum oxalat decahydrate with different heating rates

本文采用转化率α为0.1、0.3、0.5、0.7、0.9五个点.将图3的四步反应的数据计算带入公式(3)中，得到La2(C2O4)3·10H2O的活化能E如表1所示.

由表1可见，此法计算的 La2(C2O4)3·10H2O 四步分解过程活化能E分别为83.92、76.04、136.26、 162.61 kJ·mol-1.

表1 La2(C2O4)3·10H2O热分解各步反应活化能结果

2.2.2 Kissinger法热分解动力学分析

在5、10、15、20、25 K·min-1的五组升温速率下，得到 La2(C2O4)3·10H2O在空气气氛下的热分解DTA曲线如图4所示.

由图4得到不同升温速率下的DTA曲线的峰值温度如表2所示.

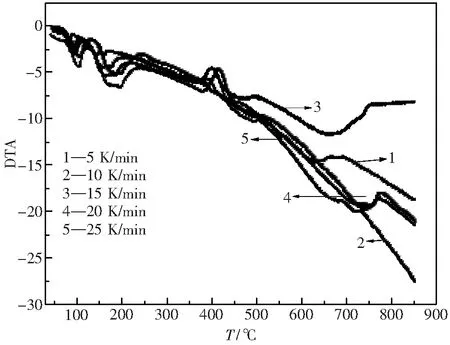
图4 La2(C2O4)3·10H2O不同升温速率下的DTA曲线 Fig.4 DTA curves of lanthanum oxalate with different heating rates

表2 不同升温速率下DTA上的峰顶温度

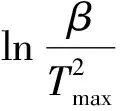
表3 La2(C2O4)3·10H2O热分解的活化能E和指前因子A

由表3可见，此法计算的La2(C2O4)3·10H2O四步分解过程活化能E分别为75.52、68.28、124.03、142.12 kJ·mol-1，指前因子A分别为4.92×1010、6.1×107、2.1×109、8.46×106s-1.

2.2.3 Crane法热分解动力学分析

将表2的Tmax带入公式(5)中，将lnβ对1/Tmax作图，线性拟合得到反应级数n如表4所示.

表4 La2(C2O4)3·10H2O热分解Crane法的反应级数n

由表4可见，Crane法处理数据得到的 La2(C2O4)3·10H2O 四步分解过程的反应级数n均为1左右.

2.2.4 同步热分析法热分解动力学分析

根据同步热分析法的公式，得到在5、 10、 15、 20、 25 K·min-1的五组升温速率下， La2(C2O4)3·10H2O 在空气气氛下的热分解TG-DTA曲线分别如图5所示.

由图5的各DTA曲线的峰顶温度和其对应温度的TG失重率换算得到如表5所示.

图5 不同升温速度下La2(C2O4)3·10H2O热分解的TG-DTA曲线Fig.5 TG-DTA curves of thermal composition of La2(C2O4)3·10H2O at different heating rates(a)—5 K·min-1； (b)—10 K·min-1； (c)—15 K·min-1； (d)—20 K·min-1； (e)—25 K·min-1

表5 不同升温速率β下DTA峰顶温度Tmax和对应TG的转化率α

经过对表5的计算，在根据Crane法的计算结果，对反应级数n在(0 ，2)之间缩放.代入式(5)计算得出活化能平均值，EC平均值如表6所示.

表6 La2(C2O4)3·10H2O在不同n值下的活化能E计算结果

由表6的结果和Crane法结果比较，进一步缩放到n=1附近，最终确定各步反应的活化能E和反应级数n，如表7所示.

表7 同步热分析法的活化能E和反应级数n

由表7可见，此法计算的La2(C2O4)3·10H2O四步分解过程活化能E分别为88.56、92.18、121.47、171.58 kJ·mol-1，反应级数n分别为1左右.

2.2.5 Coats-Redfem法热分解动机理分析

为确定第三步分解反应的机理，选择升温速率β=10 K·min-1的La2(C2O4)3·10H2O第三阶段的热分解数据，根据公式(7)来确定 La2(C2O4)3的中间产物的机理函数.一些常见的动力学机理函数如表8所示.

代入其数据到公式(7)得到斜率和截距，如表9所示.

表8 十种常见的热分解动力学机理函数

续表

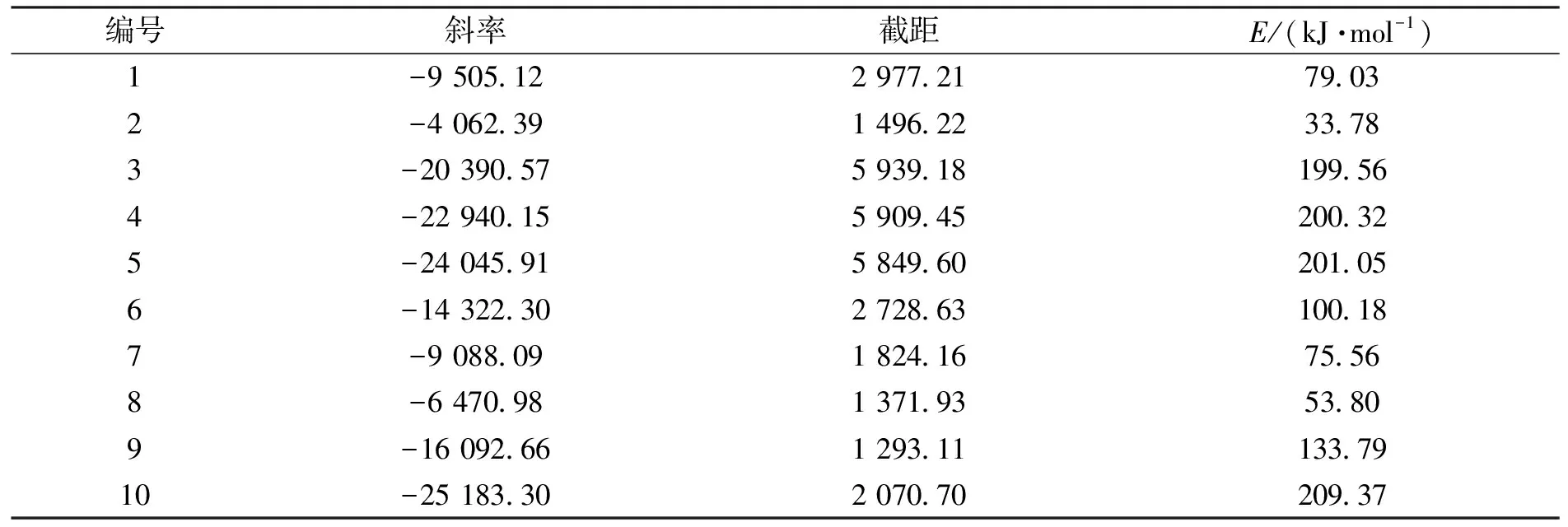
表9 Coats-Redfem积分法计算的10种模型的动力学参数

从以上Ozawa-Flynm-Wall法、Kissinger法、Crane法和同步热分析法计算结果得知，La2(C2O4)3分解为La2CO5的活化能在122.12～144.51 kJ·mol-1之间.其活化能与9号模型的计算结果吻合，由此可以判断La2(C2O4)3分解生成La2CO5为一级反应，受符号为F1的反应机理控制.对应的机理函数为f(α)=-ln(1-α)，g(α)=1-α，α为转化率.

2.3 各种方法的结果和分析比较

在使用Ozawa-Flynm-Wall法、Kissinger法、Crane法和同步热分析法对La2(C2O4)3·10H2O热分解活化能计算后，发现其计算结果基本相差不大，符合实际反应的参数，几种方法的活化能计算结果如表10所示.

表10 四种分析方法计算的活化能E

Table 10Efrom the four analysis method

Ozawa法Kissinger法Crane法同步热分析法第一步8392755283928856第二步7604682876049218第三步13626124031362612147第四步16261142121626117158

结合四种动力学分析方法的推导过程和计算结果，得到其优劣和适用性：

(1)Ozawa-Flynm-Wall法是认为不同的升温速率下起始反应温度是一样的.但是对于多步反应，可能存在前一步未能及时反应结束，就进入下一步，导致存在计算误差.这是它的机理函数选择造成的误差，可通过控制升温速率来减小误差.由于它计算简单，适合于各种化学反应.

(2)Kissinger法认为DTA的峰顶温度Tmax就是反应速率最大的温度；且反应级数n(1-α)n-1≈1，才会满足其方程式(3).因此在实际化学反应中不能完全适合，此法求得的活化能会有较大误差，但是它计算方便简单.十水草酸镧的反应技术n恰好为1左右，满足其使用条件.

(4)同步热分析法同时利用了TG和DTA曲线，尽可能地减少了实验误差.还避免了Kissinger法的使用条件限制，可以不断地缩放n值，最大精度的筛选出活化能E，但是其计算过程繁琐，且必须满足f(α)=(1-α)n.由于La2(C2O4)3分解反应受F1机理控制，满足使用条件，但是在其机理函数尚未确定的情况下，不适合使用..

3 结 论

综合以上方法和计算过程得出：La2(C2O4)3·10H2O分解过程分为四步，前两个阶段为失去结晶水，后两个阶段为La2(C2O4)3的分解反应，最终产物为La2O3.第一步：分解失去2个结晶水，生成La2(C2O4)3·8H2O，表观活化能E1在71.35～ 92.98kJ·mol-1之间，反应级数 n=1.12左右，指前因子A=4.92×1010s-1；第二步：分解失去8个结晶水，生成La2(C2O4)3，表观活化能E2在58.06～93.12kJ·mol-1之间，反应级数n=1.02左右，指前因子A=6.1×107s-1；第三步：分解生成La2CO5，表观活化能E3在122.12～144.51kJ·mol-1之间，反应级数n=1.01左右，指前因子A=2.1×109s-1，热分解过程受F1机理控制；第四步：最终分解为La2O3，表观活化能E4在153.80～170.51kJ·mol-1之间，反应级数n=0.96左右，指前因子A=8.46×106s-1.

[1]PlatovaRA,KondrukevichAA,PlatovYT.Applicationofneodymiumoxidetoincreasethewhitenessofporcelain[J].GlassCeram, 2012, 68( 11)：393.

[2]徐丽琴, 解传娣, 张雪峰, 等. 稀土永磁体研究发展动态综述[J]. 稀土, 2008, 6( 21): 89-91. (Xu Liqin, Jie Chuandi, Zhang Xuefeng,etal. Summary of rare earth magnet research and development[J]. Chinese Rare Earths, 2008, 6( 21): 89-91.)

[3]Dent P C, Rare earth elements, Permanent magnets[J]. Journal of Applied Physics, 2012, 111(7): 07-21.)

[4]谷双, 陈纪忠. 竹材热解失重动力学模型研究[J]. 高校化学工程学报, 2011, 25(2): 231-235. (Gu Shuang, Chen Jizhong. Study on pyrolysis kinetics of bamboo[J]. Journal of Chemical Engineering of Chinese Universities, 2011, 25(2): 231-235.)

[5]李稳. 一些无机水合盐的热分解动力学研究[D]. 南京: 南京理工大学, 2012： 1-10. (Li Wen. The thermal kinetics of some metal hydrated salts[D]. NanJing: Nanjing University of Science and Technology, 2012：1-10.)

[6]Genieva S D, Vlaev L T, Atanassov A N. Study of the thermooxidative degradation kinetics of poly(tetrafluoroethene) using iso-conversional calculation procedure[J]. Journal of Thermal Analysis and Calorimetry, 2010, 99(2): 550-560.

[7]方正东, 汪敦佳. 十水草酸铈分解过程和非等温动力学研究[J]. 稀土, 2005, 26(3): 19-22. (Fang Zhengdong, Wang Dunjia. Study on the thermal decomposition and non-isothermal kinetic of cerium oxalate [J]. Chinese Rare Earths, 2005, 26( 3) ：19.)

[8]胡艳红, 李梅, 柳召刚, 等. 大颗粒氧化铈的草酸盐前驱体热分解研究[J]. 稀土, 2009, 30(4): 35-37. (Hu Yanhong, Li Mei, Liu Zhaogang,etal. Study on the thermal decomposition of cerium oxalate precursor of large particle CeO2[J]. Chinese Rare Earths, 2009, 30(4): 35-37.)

[9]黄昕, 李琴, 杨明, 等. 大颗粒草酸钕热分/解特性及动力学研究[J]. 中国稀土学报, 2016, 34(1): 83-92. (Huang Xin, Li Qin, Yang Ming,etal. Thermal decomposition and kinetics analysis of larger particle neodymium oxalate[J]. Journal of the Chinese Society of Rare Earths, 2016, 34(1): 83-92.)

[10]张克立, 陈雄斌, 席美云, 等. 十水草酸镧的热分解机理[J]. 武汉大学学报(自然科学版), 1996, 42(2): 163-166. (Zhang Keli, Chen Xiongbin, Xi Meiyun,etal. Thermal decomposition of lanthanum oxalate decahydrate[J]. Journal of Wuhan University(Natural Science Edition), 1996, 42(2): 163-166.)

[11]Chen Jianping, Kimio IsA. Thermal decomposition of urea and urea derivatives by simultaneous TG/(DTA)/MS[J]. Journal of the Mass Spectrometry Society of Japan, 1998, 46(4): 299-303.

[12]Mothé C G, de Miranda I C. Study of kinetic parameters of thermal decomposition of bagasse and sugarcane straw using friedman and ozawa-flynn-wall isoconversional methods[J]. Journal of Thermal Analysis and Calorimetry, 2013, 113(2): 497-505.

[13]Barick A K, Tripathy D K. Thermal and dynamic mechanical characterization of thermoplastic polyurethane/organoclay nanocomposites prepared by melt compounding[J]. Materials Science and Engineering: A, 2010, 527(3): 812-823.

[14]Li Chunhua, Qi Shuhua, Zhang Dongna. Thermal degradation of environmentally friendly phenolic resin/Al2O3hybrid composite[J]. Journal of Applied Polymer Science, 2010, 115(6): 3675-3679.

[15]Van Humbeeck J. Simultaneous thermal analysis[J]. Handbook of Thermal Analysis and Calorimetry, 1998(1): 497-508.

[16]Mathew S, Nair C G R, Ninan K N. Thermal decomposition kinetics: Part XV. Kinetics and mechanism of thermal decomposition of tetrammine copper (II) sulphate monohydrate[J]. Thermochimica Acta, 1989, 144(1): 33-43.

[17]Laidler K J. The development of the arrhenius equation[J]. J Chem Educ, 1984, 61(6): 494.

Thermal decomposition and kinetics analysis of lanthanum oxalate decahydrate

Deng Gengfeng, Ji Chuanhong, Xie Yao, Tan Min, Cai Chenlong, Wang Yun, Zeng Qingyun

(School of Metallurgy and Chemistry Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China)

Thermal decomposition behavior of lanthanum oxalate was studied by the simultaneous thermal analysis technique TG-DTA in an air atmosphere.The thermal decomposition kinetics parameters of La2(C2O4)3·10H2O was determined by using Ozawa-Flynm-Wall method、Kissinger method、Crane method and simultaneous thermal analysis method. Curve of TG showed : the thermal decomposition of La2(C2O4)3·10H2O has 4 stages, the first two stages are the dehydration process, the succedent two stages are the thermal decomposition of La2(C2O4)3.The four stages’ apparent activation energies are 83.92、76.04、136.26、162.61 kJ·mol-1, the exponential factors are about 4.92×1010、6.1×107、2.1×109、8.46×106s-1respectively, the reaction order is about one，and the decomposition mechanism of the third step is controlled by F1 according to Coats-Redfem method.

TG-DTA；La2(C2O4)3·10H2O；thermal decomposition；kinetic parameters

10.14186/j.cnki.1671-6620.2017.02.007

TF 845

A

1671-6620(2017)02-0116-08