关于液相形核机制的思考

宋玉来, 豆志河， 刘 燕， 王国承, 张廷安

(1. 东北大学冶金学院，沈阳110819；2. 辽宁科技大学材料与冶金学院，辽宁鞍山114051)

关于液相形核机制的思考

宋玉来1, 豆志河1， 刘 燕1， 王国承2, 张廷安1

(1. 东北大学冶金学院，沈阳110819；2. 辽宁科技大学材料与冶金学院，辽宁鞍山114051)

通过对比经典形核理论与二步形核理论，结合第一性原理计算，引出经典形核理论的不足之处.二步形核理论认为，液相析出固态结构的过程经历了一个由液相内部局部波动(结构或浓度)而引发的簇状结构的生成，此类簇状结构一部分在随后的碰撞中分解消失，一部分相互连接而长大，而基于我们当前对形核的认识，实际形核是一个极其复杂的多步过程.

经典形核理论；二步形核理论；第一性原理；簇状结构

由熔体中析出结晶固体的现象普遍存在于自然界和工业过程中，生产得到的材料产品运用于国民生活中.不同的行业对材料的性能提出了不同的要求，如具有优良的电学、磁学、光学、热学、声学、力学、化学、生物医学功能，以及特殊的物理、化学、生物学效应，能完成功能相互转化，主要用来制造各种功能元器件而被广泛应用于各类高科技领域的功能材料；以力学性能为基础，以制造受力构件所用材料，同时对物理或化学性能(如光泽、热导率、抗辐照、抗腐蚀、抗氧化等)也有一定要求的结构材料.这些材料的制备都经历了初期的形核过程，其中形核的数量和形状特性又决定了后期结晶的结构和粒度分布.在过去的几十年里，研究者们对于离子材料(例如碳酸钙、蛋白质和有机分子晶体)进行了大量的实验和分子模拟研究，发现结晶固体从溶液中的析出过程并没有经历已为当前研究者们所普遍接受的经典形核过程(Classical Nucleation Process, CNP)，而是经历了一个更为复杂的包含多种潜在机制的多步形核过程(Multi-step Nucleation Process, MSNP)[1-3].对于金属熔体，研究者在金属的冶炼过程中对高温Fe-O-Al体系中氧化铝团簇与溶解氧之间的热力学关系[4]、在不锈钢与轴承钢冶炼过程中镁铝尖晶石夹杂物(MgO·Al2O3)的形成机制[5]、对以均匀形核为主导的微晶金属陶瓷的形核体系[6-8]的研究过程也同样发现一些难以用经典形核理论解释的现象；而运用最近提出的多步形核理论却可以得到较为满意的解释.当然对于晶态固体(包括晶体、类晶体、团簇和无定形结构)的实际形核过程究竟是以哪种方式形核，对于不同的体系众说纷纭，并没有形成一致的观点.本文基于当前研究现状，对当前对形核机理的认识做了一个大概描述，形核过程也一直是凝固结晶领域的一个研究热点，受到各地研究者们的普遍关注.

1 经典形核理论的描述

1.1 经典形核理论

经典形核理论(Classical Nucleation Theory, CNT)是用来描述形核过程最为简单和广泛的理论，它最初在19世纪由吉布斯对水蒸气凝结为液态水的过程研究中得出，并被后来的研究者推广运用到解释从过饱和溶液和熔体中析出晶体的过程，尽管存在一些缺陷，但仍然为大多数研究者所接受，并在很长的一段时间内占据主导地位.

依据吉布斯的动力学理论机制，溶液的稳态形核率，即单位时间单位体积的形核数量J可以表示为

(1)

其中，k是玻尔兹曼常数，A为前置因数.A的理论值为1030cm-3·s-1，由于分子的移动速率随温度的变化显著，事实上很难获得A的准确值.

吉布斯认为溶液内团簇的形成能ΔG由相变能ΔGv和形成界面的表面自由能ΔGs组成，

ΔG=ΔGv+ΔGs

(2)

对于过饱和溶液，相变能ΔGv表示溶液中由于局域波动而引起的分子或原子发生聚合作用的趋势，相比于液态，固态的自由能更低，也表现得更为稳定，此过程中ΔGv为负值，从而使体系的吉布斯自由能降低，对于界面自由能ΔGs，由于生成了界面，使体系的能量升高，并且随着体系内部该种形式的颗粒增加，能量增加的趋势明显，它显然不利于形核的继续进行，液态的形核过程就是在这两种能量的共同控制下进行，自由能变化(ΔG)随粒子半径r的变化趋势可以用图1表示.

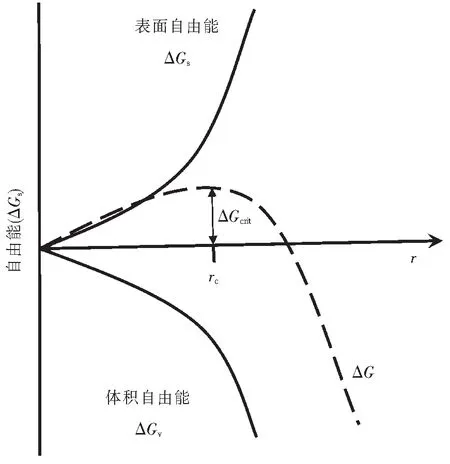
图1 吉布斯自由能随粒子半径的变化过程Fig.1 Variation process of Gibbs free energy with particle radius

1.2 经典形核理论的缺陷

经典形核理论在描述一些形核过程中得到了令人满意的结果，但是也存在固有的缺陷，具体可以简要描述为如下几个方面：

(1)经典形核理论近似认为团簇的演化仅仅是由原子间的连接与断开过程，而忽略了原子(团)之间的碰撞，这种观念在后期的分子模拟凝固过程中得到了否定，事实上碰撞过程对形核影响显著[1].

(2)在对水凝结的形核率计算方面，经典形核理论与云室实验(cloud chamber experiment)计算的数值相差1～2个数量级[9]，对于乙醇蒸气的凝聚过程，实验与理论的值浮动在10-10到107之间[10].对于多组分的液态体系，由于对温度的依赖作用明显，对单一组分的非极性流体的气液转变，经典形核理论的计算是定性合理，但在定量上具有较大的差距.

(3)经典形核理论认为，形核的粒度分布随时间是不变的，这显然与实际溶液的结晶过程不符，并且在形核过渡期未能给出亚临界团簇的稳态分布[11].

(4)关于液滴的宏观热力学描述是否可以用来模拟仅包含数十个分子(原子)的小团簇的性质在相当长的时间段里一直争议不断[12-13]，我们知道临界晶核尺寸一般包含100～1 000个原子之间，根据Yau和Vekilov的研究结果[14],表面张力在原子数少于100时的表征已经非常不准确，对于那些仅包含20～50个原子的小团簇，经典形核理论显然已不再适用.

2 二步形核理论的描述

二步形核理论最初是由Wolde和Frenke[15-16]运用蒙特卡罗方法(Monte Carlo technique，MC)对具有短程相互作用的L-J体系的均匀形核过程研究中提出来的.该理论认为在远离相变点的区域，体系的结构和密度变化是连续的，体系的形核过程是由局域的温度或密度波动引起了自由能的变化，从而出现一些类液相(liquid-like)的簇状结构，这些结构在随后的过程中一部分通过碰撞或原子吸附而长大，另一部分则又被重新破碎分解，只有那些达到了临界状态的簇状结构才可以转化为临界晶核保存在溶液中进一步长大.二步形核理论与经典形核的对比示意图如图2所示.

图2 经典形核与二步形核过程的对比示意图Fig.2 Comparison diagram between the classical nucleation and the two-step nucleation

3 两种形核理论在实际体系中的应用

3.1 经典形核理论在过冷液态金属和合金体系中的应用

金属和合金体系可以在低于液相线很远的一段区间内保持一段时间而不发生凝固，在形成一个更稳定相之前存在一个能垒.由于液态金属和合金的性质相似，形核需要克服的能垒很小，但过冷金属或合金熔体通常表现出不寻常的稳定性来抑制晶化过程.经典形核理论往往不能准确预测界面两侧的结构变化，同时对固液相变的理论处理需要加入局域序参数的波动[17].根据人们对液态金属结构认识的深化和新的研究结果,同样对凝固过程中形核核心的形成也可以从新的角度来认识.如果液态金属中有能够稳定存在的中、短程序原子团, 那么假设这种稳定存在的中、短程序的原子团是晶胚,而液态金属中可以形成凝固形核核心的晶胚就成为一种客观存在.当温度改变时,液态金属中的晶胚的尺度和不同尺度晶胚的几率在随之改变, 如图3所示[18].温度升高,大尺度晶胚减小,小尺度晶胚增加;温度降低,大尺度晶胚数量增加,小尺度晶胚数量减少.

图3 不同温度(T1>T2>T3>Tm)下金属液中晶胚的变化Fig.3 Variation of embryos in molten metal at different temperatures (T1>T2>T3>Tm)

合金的沉积动力学可以用来预测合金的性质，经典形核理论可以用来预测多种二元合金体系的形核率均有较好的结果，比如Al-Zr, Al-Sc以及部分三元合金体系如Al-Zr-Sc[19].当这些合金体系中考虑短程序时，不管是与实验值还是模拟结果相比都有较好的吻合度.

3.2 基于二步形核理论硅脱氧过程氧化硅形核路径的探讨

基于硅脱氧反应在冶炼洁净钢过程中的重要地位，近年来各国的学者已对其进行了大量的研究[20-24]，Wasai等[24]在对铜的硅脱氧实验中发现了球状和珊瑚状的氧化硅夹杂物，根据经典形核理论，硅脱氧温度下形成的稳定的氧化硅夹杂物应该是方石英及其复合物，这与实验发现的现象完全不符，因此我们运用基于第一性原理(density functional theory , DFT)的分子模拟计算了Fe-O-Si体系中氧化硅的形成路径，(SiO2)n(n=2～10, 14, 20)生成和转化的吉布斯自由能变化如图4所示.

从图中可以看出，炼钢温度下团簇生成的吉布斯自由能均为负值，而当团簇向晶体转变时的吉布斯能变化只有在n<4时才为负值，说明此条件下团簇生成均能自由生成，而此后则只有小团簇(n<4)可以发生转化成为晶体，而剩余团簇在随后的冷却过程中转变为无定形结构夹杂物.

(SiO2)n(n=2～10, 14, 20)的热力学计算结果与氧化硅实验值(实心)和氧化铝实验值(空心)的关系如图5所示.

图4 团簇生成(a)和转化(b)的吉布斯自由能变化关系Fig.4 Variation of Gibbs free energy for cluster formation (a) and transformation (b)

图5 炼钢温度(1 873 K)下log {w[Si]%, w[Al]%}和log {w[O]%}的关系Fig.5 Relationship between log {w[Si]%, w[Al]%} and log {w[O]%} at 1 873 K

从图中可以看出，在炼钢温度下硅脱氧的实验值基本上都落在团簇线(细虚线)之下，氧化硅的形成经历了以下三个阶段：1)团簇生成.在团簇线(cO,Sic)区域，团簇稳定性随过剩氧的降低而增加，当熔体中硅的含量和温度不变时，此区间的团簇不稳定并随着成分而变化. 2)团簇聚集.在团簇线(cO,Sic)和临界团簇线(cO,Sicr)之间的区域最稳定的是(SiO2)20团簇，此区域具有不同形状和尺寸的团簇之间可以自发地链接聚集，该处的硅氧浓度应该和远低于临界尺寸的团簇聚集体保持平衡.3)类晶体团簇.在团簇线(cO,Sic)和最稳定团簇(SiO2)20与固态氧化硅平衡氧浓度曲线(cOSiO2(s))之间，此区域氧化硅团簇和晶体氧化硅夹杂物共存，因此，硅脱氧过程的氧化硅形成路径可以用下式表示.

[Si]+[O](SiO2)nSiO2(s)

(3)

我们进一步计算了团簇演化随温度降低的变动情况，将两个典型温度点(1 623 K，1 873 K)的计算结果作图可以反映熔体中夹杂物形核随温度降低的变化过程，如图6所示.

3.3 溶盐溶液的二步形核机制

研究者们同样对于NaCl溶盐体系做了大量的研究来探索预形核团簇，对大尺度的微过饱和氯化钠溶液的分子动力学模拟研究发现该体系的形核经历了一个复杂的二步形核过程，在这个过程中密度起伏先于结构起伏[25].图7表明，在 3 ns 时，体系内部局域出现了超出体系浓度的无规则的稠密结构相，7 ns时此结构进一步趋于重构变的有序化，空间有序结构包含的原子数量变化为218→249，该高密度区域包含了一定数量的水(分子)(用红色表示)，随着晶体的生长，内部的水分子逐渐被排除直到最终的无水氯化钠的生成.这个模拟实验是初期由蛋白质和生物矿物研究提出的二步形核机制的一个印证，图7中c和d清晰表明晶体区域通过从溶液中获取粒子而长大.显然可以看出预形核团簇的结构跟最终的稳定态构型并不相同，说明实际结晶是一个复杂的多相过程.

图6 硅脱氧过程的吉布斯自由能变化过程示意图Fig.6 Gibbs free energy change in process of silicon deoxidation

图7 在300 K，101 kPa压力下包含64 000个粒子的大尺度分子动力学模拟[25]Fig.7 Large scale molecular dynamic simulation of system containing 64 000 particles at 300 K, 101 kPa

4 总结与展望

从多种不同形核体系的对比分析得出，虽然经典形核理论发展较早，也最简明完善，但是在解释某些特定体系时遇到了较大的困难.近年来发展的更为复杂的二步形核理论在解释形核问题时更为贴切，具有较强的适用性，但由于液相中析出固相的形核过程是一个极其复杂的多步过程，其中可能同时伴随着簇状聚集体的连接与分解；我们当前对这部分的理解还具有较大的局限性，未来需要我们进一步加深对这个过程的认识，依然需要发展更为完善的理论来作为引导.

[1]Deniz E, Alfred Y L, Allan S M. Nucleation of crystals from solution: classical and two-step models [J]. Accounts of Chemical Research, 2009, 42 (5), 621-629.

[2]Peter G V. Nucleation [J]. Crystal Growth Design, 2010, 10(12), 5007-5019.

[3]Sear R P. The non-classical nucleation of crystals: microscopic mechanisms and applications to molecular crystals, ice and calcium carbonate [J]. International Materials Reviews, 2012, 57:6, 328-356.

[4]Wang G C, Wang Q, Li S L,etal. Evidence of multi-step nucleation leading to various crystallization pathways from an Fe-O-Al melt [J]. Scientific Reports, 2014, 4, 5082.

[5]Zong N F, Liu Y, He P. Learning about the nucleation pathway of MgO·Al2O3spinel from an Fe-O-Al-Mg melt using a two-step nucleation mechanism [J]. RSC Advance, 2015, 5, 48382-48390.

[6]Berezhnoi A I. In Glass-Ceramics and Photo-Sitalls [M]. Springer: Berlin, 1970, 275.

[7]Robert C R. Superheated Liquids: Liquids in the superheated state, far from being a laboratory curiosity, occur more often than thought and may cause industrial accidents [J]. American Scientis, 1976, 64 (2), 146-156.

[8]Wegener P P. Nonequilibrium flow with condensation [J]. Acta Mechanica, 1975, 21 (1-2), 65-91.

[9]Mostafa A S, Richard A D. A comparison of measured nucleation rates with the predictions of several theories of homogeneous nucleation [J]. The Journal of Chemical Physics, 1982, 77, 1517.

[10]Strey R, Wagner P E, Schmeling T. Homogeneous nucleation rates for n-alcohol vapors measured in a two-piston expansion chamber [J]. 1986, 84, (4), 2325.

[11]Knezic D, Zaccaro J, Myerson A S. Nucleation induction time in levitated droplets [J]. The Journal of Physical Chemical B, 2004, 108 (30), 10672-10677.

[12]Strey R, Viisanen Y. Measurement of the molecular content of binary nuclei. Use of the nucleation rate surface for ethanol-hexanol [J]. The Journal of Chemical Physics, 1993, 99, 4693.

[13]Mokross B J. Nucleation theory and small system thermodynamics [J]. Materials Physical Mechanics, 2003, 6, 13-20.

[14]Yau S T, Vekilov P G. Direct observation of nucleus structure and nucleation pathways in apoferritin crystallization [J]. Journal of American Chemical Society, 2001, 123(6), 1080-1089.

[15]Wolde T P R, Frenkel D. Enhancement of protein crystal nucleation by critical density fluctuations [J]. Science, 1997, 277, 1975-1978.

[16]Myerson A S, Trout B L. Nucleation from Solution [J]. Science, 2013, 341, 855-856.

[17]Russo J, Tanaka H J. The microscopic pathway to crystallization in supercooled liquids [J]. Soft Condensed Matter, 2010, 12, 12001.

[18]王建中. 经典凝固形核问题的思考 [J]. 辽宁工学院学报，2001, 21(6), 30-32. (Wang Jianzhong. Cogitation on the problem of classical solidification nucleation [J]. Journal of Liaoning Institute of Technology, 2001, 21(6), 30-32.)

[19]Karthika S, Radhakrishnan T K, Kalaichelvi P. A review of classical and nonclassical nucleation theories [J]. Crystal Growth Design, 2016, 16 (11), 6663-6681.

[20]Suzuki K, Ya S B, Hino M. K. Deoxidation equilibrium of chromium stainless steel with Si at the temperatures from 1823 to 1923 K [J]. ISIJ international, 2001, 41(8), 813-817.

[21]Itoh T, Nagasaka T, Hino M. Phase equilibria between SiO2and iron-chromite spinel structure solid solution, and deoxidation of liquid Fe-Cr alloy with silicon [J]. ISIJ International, 2002, 42, 33-37.

[22]Liu Z Z, Wei J, Cai K. A coupled mathematical model of micro-segregation and inclusion precipitation during solidification of silicon steel [J]. ISIJ International, 2002, 42, 958-963.

[23]Iwamoto N. Structural problems of the deoxidation products in steel [J]. Tetsu-to-Hagané, 1972, 58, 787-810.

[24]Wasai K, Mukai K. Mechanism of formation of amorphous silica inclusion in silicon deoxidized copper [J]. ISIJ International, 2003, 43, 606-611.

[25]Chakraborty D, Patey G N. How crystals nucleate and grow in aqueous NaCl solution [J]. Jonrnal of Physical Chemistry Letters, 2013, 4 (4), 573-578.

A cogitation on the nucleation mechanism of liquid phase

Song Yulai1, Dou Zhihe1, Liu Yan1, Wang Guocheng2, Zhang Tingan1

(1. School of Metallurgy, Northeastern University, Shenyang 110819, China; 2. School of Materials and Metallurgy, University of Science and Technology Liaoning, Anshan 114051, China)

Combined with the first principle calculation, the authors compared the classical nucleation theory with the two step nucleation theory. It was found that the classical nucleation theory have some deficiencies. The two step nucleation theory believed that the process of the solid structure formation from liquid phase went through a local fluctuations (structure or concentration) in internal liquid phase to generate a cluster structure. A part of the cluster structure disappeared in the subsequent collision, while the other part will grow up through connection with each other. Based on the authors’ understanding, the actual nucleation is a complex multistep process.

classical nucleation theory; two-step nucleation theory; first principles; cluster structure

10.14186/j.cnki.1671-6620.2017.02.004

TG 146.1

A

1671-6620(2017)02-0098-06