基于校正余数筛选的余弦信号频率估计

张 威，李 松，李 林，刘进忙

(1.空军工程大学防空反导学院，陕西 西安 710051； 2.西安电子科技大学电子工程学院，陕西 西安 710071)

基于校正余数筛选的余弦信号频率估计

张 威1，李 松1，李 林2，刘进忙1

(1.空军工程大学防空反导学院，陕西 西安 710051； 2.西安电子科技大学电子工程学院，陕西 西安 710071)

针对高欠采样余弦信号频率估计精度差的问题，提出了基于校正余数筛选的余弦信号频率估计算法。该算法运用FFT相位差法求得任意初始参考相位估计值，结合插值方法对频率和相位进行高精度校正，给出了一种降低参考相位估计精度的余数筛选方案，将简化后的闭合形式中国余数定理推广到实数域。仿真结果表明：在有噪声时，所提算法的频率估计精度优于现有算法；在低信噪比时，所提算法的频率估计均方误差远远低于现有算法。

频率估计；相位估计；中国余数定理；余数筛选

0 引言

频率估计[1-2]在雷达、通信等领域有着广泛的应用，如何提高精度的同时又降低对设备的要求，一直是频率估计的研究热点。为了解决欠采样高频信号频率估计问题，文献[3]将中国余数定理(Chinese remainder theorem，CRT)引入该领域。CRT告诉我们：如果一个整数小于一组两两互质的数的最小公倍数，则该数可由其取模运算后的余数唯一地确定下来。由于余数错误会对CRT重构产生较大误差，限制了CRT的应用，为此提出了两种方法：余数数目冗余方法[4]和余数冗余方法[5-7]。文献[3]利用余数的冗余来鲁棒的恢复原数，但是搜索算法复杂度较大。文献[6]提出了一种鲁棒的CRT闭式求解方法，大大降低了运算量，并推广到实数域，扩大了应用范围。文献[7]提出了一种更简洁的闭式CRT表达式，进一步降低了运算量,但没有推广到实数域。目前多数的CRT应用在复数频率估计场合(如合成孔径雷达系统的相位解缠绕[5])，文献[8]首次利用CRT解决了欠采样下的实数余弦信号的频率估计问题，但该文献只解决了特定初相的频率估计问题，而且文中的频谱校正方法精度不高。本文针对此问题，提出了基于校正余数筛选的余弦信号频率估计算法。

1 频率估计原理

1.1 鲁棒的闭式CRT算法

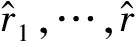
K≡rimodMi

(1)

式中，0≤ri≤M，i=1,…,L。正整数K小于模M1,…,ML的最小公倍数，便可以求出其唯一解。

假设模M1,…,ML的最大公约数为N，且除去最大公约数后的模两两互质，即Mi=NΓi，且gcd(Γi,Γj)=1,i≠j，gcd(·)表示最大公约数。如果余数存在误差，正整数K的求解过程如下：

(2)

(3)

(4)

(5)

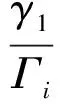
(6)

1.2 余弦信号的CRT模型

n=0,…,N-1;i=1,…,L

(7)

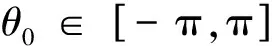
(8)

对式(8)变形，得

(9)

从式(9)可以发现：待测频率的估计问题实质上就是CRT重构问题，其中采样频率对应于余数定理中的模值，右边式子的第二项则对应于余数定理中的余数值，即

(10)

从式(9)可看出：采样频率作为已知参数，待估计频率值的精度取决于余数的估计精度。因此，本文引入频谱校正提高余数估计精度(文献[5]中舍弃了δi而影响了余数估计精度)。

1.3 基于CRT的频率估计方案

根据余弦信号的CRT模型，文献[8]给出了一种欠采样余弦信号的频率估计方案，其具体步骤：

1)对高频模拟信号做过零点检测，任取某过零点作为起始采样位置；分别以L路欠采样速率对高频模拟信号做并行采样，每路均采集N个样点。

1.4 改进的频率估计方案

文献[8]的方案在实际应用中存在一些问题，比如：采样路数过多，造成系统过于复杂；对于任意初相，导致算法失灵；频率校正方法精度不高，无法提供高精度余数；闭合形式的CRT表达式不够简洁，带来计算量的增加。针对上述问题，在满足精度的要求下，本文只进行了三路采样，改进的频率估计方案如图1所示。

2 基于校正余数筛选的频率估计算法

2.1 初相检测

若待估计信号的初始相位值为90°或-90°，可以考虑对信号作过零点检测[8]求出相位估计值。假设实际检测过程中信号的幅值由正值变为负值记为90°，反之则为-90°。过零点的瞬间相位将为后面的余数筛选提供相位参考，在工程上仅需借助简单的触发电路即可实现过零点类型检测。

若待估计信号的初始相位值未知，可以参考文献[9]给出的FFT相差法进行相位估计，该方法估计精度较高。

2.2 余数校正

对信号作FFT后获得的幅度谱和相位谱存在以下问题：幅度谱存在泄漏；峰值谱的相位值紊乱，不等于真实相位值(见图2)。由于余数的错误会导致CRT的重构产生较大错误。因此，对信号的频率校正非常有必要。

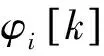
步骤2：利用频谱峰值位置km及其左右两点频谱值，用下式作频偏估计。

Liang算法：

(11)

Fang算法：

(12)

(13)

(14)

则可计算出相应的CRT余数估计值为

(15)

2.3 余数筛选

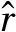
(16)

通过上式计算，选出距离较小的相位值，并将其所对应的频率值作为余数输出。通过3.1节分析可以发现：两个相位估计值的符号相反。因此，参考相位θ0的符号检测比估计精度对上述距离比较产生的影响更大。在实际应用中，应重点关注初相符号检测。

2.4 推广的闭式CRT处理过程

(17)

3 仿真分析

3.1 余数估计分析

φ1(641)=-105.66°，φ1(1 407)=105.66°，

φ2(972)=60.35°，φ2(1 076)=-60.35°，

φ3(987)=80.00°，φ3(1 061)=-80.00°；

参考初相值为-90°，则筛选出的余数估计值分别为：

Liang算法相位校正值分别为：

φ1(641)=-105.66°，φ1(1 407)=105.66°，

φ2(972)=60.35°，φ2(1 076)=-60.35°，

φ3(987)=80.00°，φ3(1 061)=-80.00°；

参考初相值为-90°，则筛选出的余数估计值分别为：

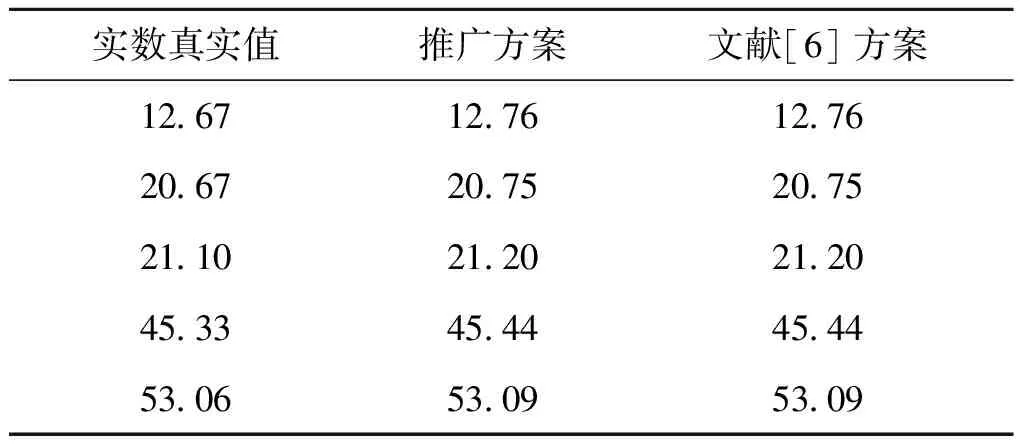
由此可以看出：在没有噪声的情况下，Candan算法和Fang算法的余数估计精度相同。

信号路数i=1i=2i=3峰值位置K值641140797210769871061相位值/(°)-72 0472 04118 61-118 6197 68-97 68

3.2 估计方案性能分析

由图4可知：当信噪比处于-2～20dB之间，除了Quinn校正的估计精度较差外，其他方法估计精度不相上下；当信噪比处于13～20dB之间，Liang校正和Fang校正的性能略微下降；但是当信噪比处于-10～-2dB之间时，Liang校正和Fang校正的精度远远高于其他三种方法。在实际工程应用中，Liang校正因要求解反正切值，需占用存储器，更倾向于使用Fang校正。

4 结论

本文提出了基于校正余数筛选的余弦信号频率估计算法。该算法运用FFT相差法完成了对未知参考初相的估计，解决了算法局限于特定初相的问题；分别运用Liang估计器和Fang估计器作为频率和相位校正方法，解决了Candan估计器余数估计精度低的问题，进一步提高了估计精度；给出了一种降低参考相位估计精度的余数筛选方案；对现有简化的闭合形式CRT，将其推广到实数域，扩大了算法适用范围。仿真结果表明：在有噪声时，所提算法的频率估计精度优于现有算法；在低信噪比时，所提算法的频率估计均方误差远远低于现有算法。

[1]李夏，郭英，张坤峰，等.基于频移修正的线性方程频率估计算法[J].探测与控制学报，2015，37(4)：66-71.

[2]谢胜，于平，林少兴，等.基于频移修正的奎因频率估计算法[J].探测与控制学报，2012，34(1)：50-54.

[3]XiaXG,WangG.PhaseunwrappingandarobustChineseremaindertheorem[J].IEEESignalProcessingLetters,2007,14(4):247-250.

[4]GoldreichO,RonD,SudanM.Chineseremainderingwitherrors[J].IEEETransactionsonInformationTheory,2000,46(4):1330-1338.

[5]LiXW,LiangH,XiaXG.ArobustChineseremaindertheoremwithitsapplicationsinfrequencyestimationfromundersampledwaveforms[J].IEEETransactionsonSignalProcessing,2009,57(11):4314-4322.

[6]WangWJ,XiaXG.Aclosed-formrobustChineseremaindertheoremanditsperformanceanalysis[J].IEEETransactionsonSignalProcessing,2010,58(11):5655-5666.

[7]王文杰，李小平. 鲁棒的闭式中国余数定理及其在欠采样频率估计中的应用[J].信号处理,2013,29(9):1206-1211.

[8]黄翔东,丁道贤,南楠,等.基于中国余数定理的欠采样下余弦信号的频率估计[J].物理学报,2014,63(19):198-203.

[9]齐国清,贾新乐.基于DFT相位的正弦波频率和初相的高精度估计方法[J].电子学报,2001,29(9):1164-1167

[10]LiangXH,LiuAJ,PanXF,etal.Anewandaccurateestimatorwithanalyticalexpressionforfrequencyestimation[J].IEEECommunicationsLetters,2016,20(1):105-108.

[11]FangLY,DuanDL,YangLQ.AnewDFT-basedfrequencyestimatorforsingle-tonecomplexsinusoidalsignals[C]//MILCOM2012-2012IEEEMilitaryCommuni-icationsConference.Piscataway:IEEE,2012:1-6.

[12]CandanC.AmethodforfineresolutionfrequencyestimationfromthreeDFTsamples[J].IEEESignalProcessingLetters,2011,18(6):351-354.

[13]JacobsenE,KootsookosP.Fast,accuratefrequencyestimators[J].IEEESignalProcessingMagazine, 2007,24(3):123-125.

[14]QuinnBG.EstimatingfrequencybyinterpolationusingFouriercoefficients[J].IEEETransactionsonSignalProcess,1994,42(5):1264-1268.

Frequency Estimation of Cosine Signal Using Remainder Correction Screening

ZHANG Wei1，LI Song1，LI Lin2，LIU Jinmang2

(1.Air and Missile Defense College，Air Force Engineering University，Xi’an 710051，China； 2.School of Electronic Engineering，Xi Dian University，Xi’an 710071，China)

To solve the poor estimation accuracy in high-undersampling frequency estimation of cosine signal, a new frequency estimation algorithm was proposed, which was based on remainder correction screening. Firstly, a FFT phase difference measuring method estimate the unknown initial reference phase. Furthermore, through applying interpolation method for high precision frequency and phase correction of each undersampling, a reminder filtering scheme was adopted to reduce the reference phase estimation accuracy requirement as well as choosing. Finally, the simplifying closed-form Chinese remainder theorem was generalized to reals, which acquired last frequency estimation. Simulation results showed that the frequency estimation accuracy of the proposed algorithm was higher in noisy environment, and the mean square error of the proposed algorithm was lower in low signal-to-noise ratio, which was better than the existing algorithms.

frequency estimation；phase estimation；Chinese remainder theorem；remainder screening

2017-01-09

张威(1990—)，男，陕西户县人，硕士研究生，研究方向：雷达数字信号处理。E-mail:wzhang1990@yeah.net。

TN911.7

A

1008-1194(2017)03-0107-05