小口径火炮弹头触发引信机械零件质量散布特性

刘 鹏，王雨时，闻 泉，张志彪

(南京理工大学机械工程学院，江苏 南京 210094)

小口径火炮弹头触发引信机械零件质量散布特性

刘 鹏，王雨时，闻 泉，张志彪

(南京理工大学机械工程学院，江苏 南京 210094)

为了找出引信机械零件质量散布特性规律，从而提高引信产品工程设计质量、安全性和可靠性，以小口径航炮弹头触发引信和高炮弹头触发引信为样本，利用数理统计方法获得了其机械零件质量散布特性。这两种引信零件质量总的散布特性规律相近；约有半数品种的零件质量散布服从正态分布或Weibull分布；还有约50%的零件种类不服从典型分布；结构维数越多，零件的质量散布越大；无表面处理的零件质量散布较大；平均尺寸精度等级对零件散布特性影响不明显，每降低一个等级，零件质量散布约增大0.5%。

引信；数理统计；零件质量；散布特性

0 引言

引信发射时所受过载最大可达十几万g，零部件质量变化对其后坐力影响较大，进而影响发射强度和后坐(惯性)保险机构解除保险可靠性[1]，因此研究引信零部件的质量散布特性对于确保产品工程设计质量、提高引信安全性和可靠性具有重要意义。对于极少数简单几何形状的零件，因其材料密度变化不大，理论上可以采用全微分方式求出其质量散布受尺寸误差影响的数学关系式。但对绝大多数的零件，由于组合后的几何形状过于复杂，所以工程实践上多用数理统计的方法来研究其质量散布特性[2]。文献[3]以小口径高炮弹头触发引信机械零件为例，利用数理统计方法，获得了其机械零件质量散布特性与由这些机械零件随机组合而成的引信产品质量散布特性，但由于积累数据较少，样本量小，未得到明显散布特性。本文在文献[3]研究的基础上，加大实测质量数据样本量开展研究，试图进一步找出引信机械零件质量散布特性规律。

1 分析方法与样本概况

1.1 分析方法

非参数检验是统计分析方法的重要组成部分，它与参数检验共同构成统计推断的基本内容。非参数检验是在总体分布未知或知道甚少的情况下，根据来自总体的样本对总体的分布进行推断，并利用样本数据对总体分布形态等进行推断的方法。

常用的非参数检验方法有卡方检验、二项分布检验、K-S检验以及变量值随机性检验等方法。K-S检验方法能够利用样本数据推断样本来自的总体是否服从某一理论分布，是一种拟合优度的检验方法，适用于探索连续型随机变量的分布。一般认为K-S检验法可直接处理原始数据，且在样本不大时也可使用[4-6]。本文利用Matlab自带工具箱直接对各样本进行参数估计，并选择K-S检验法对所得参数进假设检验[7-8]。

1.2 样本概述

以一种小口径航炮引信18种机械零件和6种部件的合格品各200件称重数据为样本，零件质量均值、标准差和极值如表1所列，频数分布直方图如图1所示；部件质量均值、标准差和极值如表2所列，频数分布直方图如图2所示。

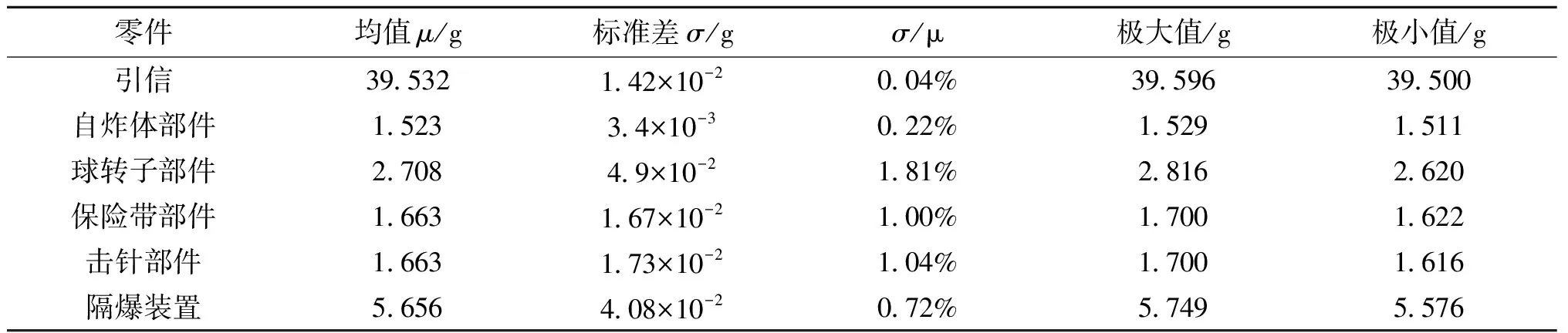
表2 各部件质量均值、标准差和极值

2 参数估计和分布拟合

据前人研究，分别对各零件质量散布进行正态分布假设和Weibull分布假设，并进行参数估计和分布拟合检验。各零件质量散布拟合参数如表3所列；零件特征和散布检验结果如表4所列，其中尺寸数大于4的零件，其平均尺寸精度等级为前4个最大尺寸的精度等级均值四舍五入后取整数；各部件质量散布拟合参数如表5所列，部件特征和散布检验结果如表6所列。

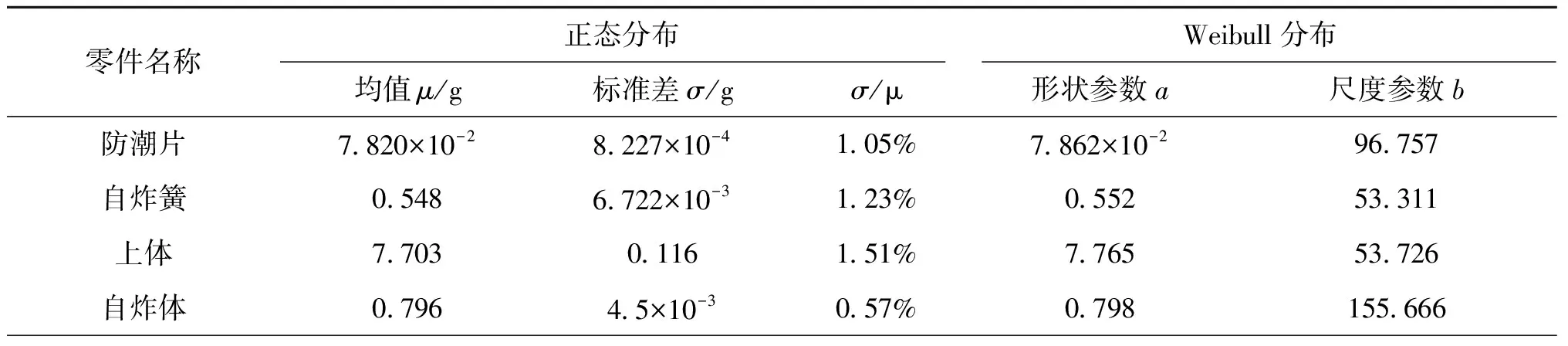
表3 各零件质量散布参数

续表

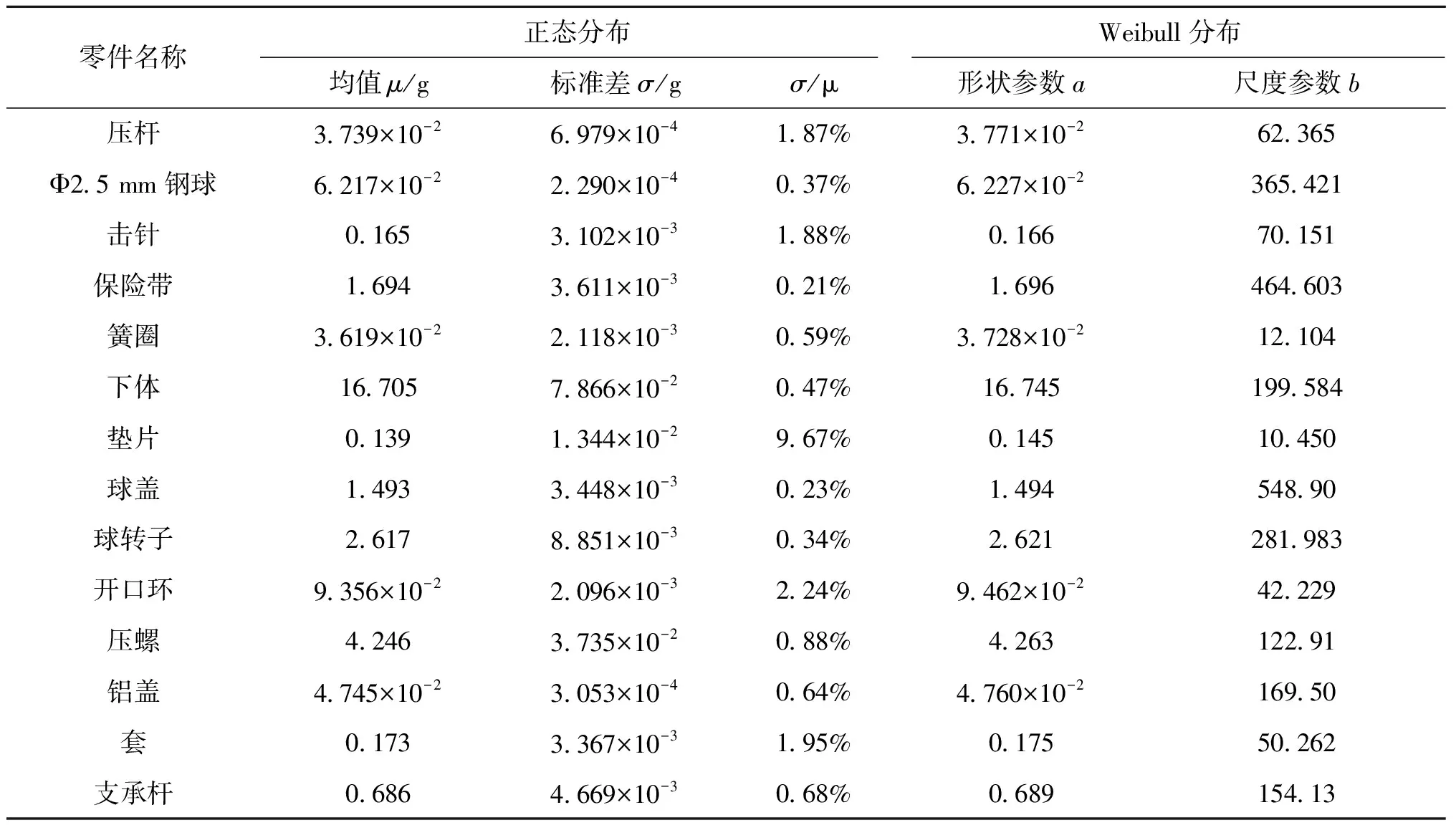
零件名称正态分布Weibull分布均值μ/g标准差σ/gσ/μ形状参数a尺度参数b压杆3 739×10-26 979×10-41 87%3 771×10-262 365Φ2 5mm钢球6 217×10-22 290×10-40 37%6 227×10-2365 421击针0 1653 102×10-31 88%0 16670 151保险带1 6943 611×10-30 21%1 696464 603簧圈3 619×10-22 118×10-30 59%3 728×10-212 104下体16 7057 866×10-20 47%16 745199 584垫片0 1391 344×10-29 67%0 14510 450球盖1 4933 448×10-30 23%1 494548 90球转子2 6178 851×10-30 34%2 621281 983开口环9 356×10-22 096×10-32 24%9 462×10-242 229压螺4 2463 735×10-20 88%4 263122 91铝盖4 745×10-23 053×10-40 64%4 760×10-2169 50套0 1733 367×10-31 95%0 17550 262支承杆0 6864 669×10-30 68%0 689154 13

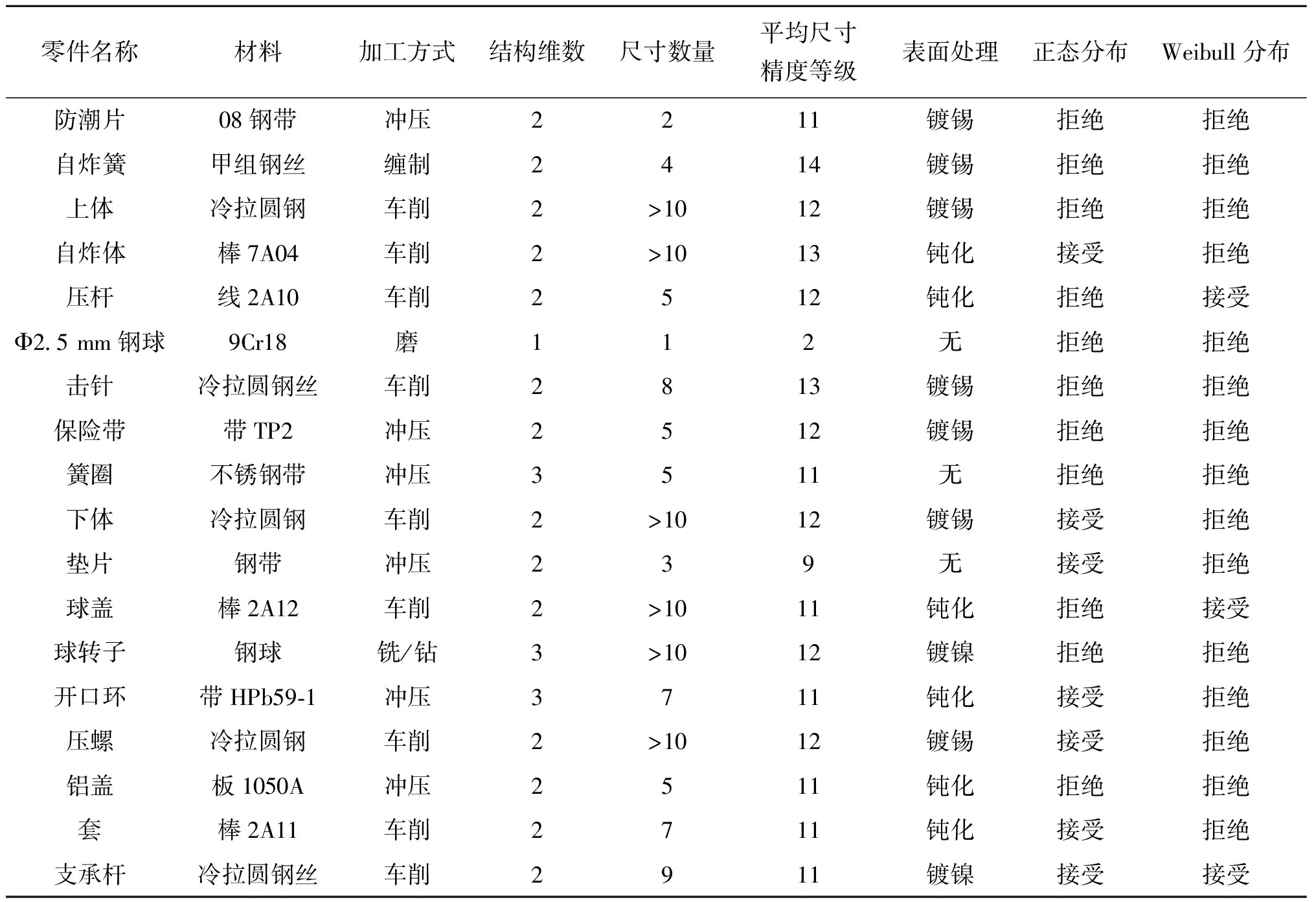
表4 各零件特征和散布拟合检验结果

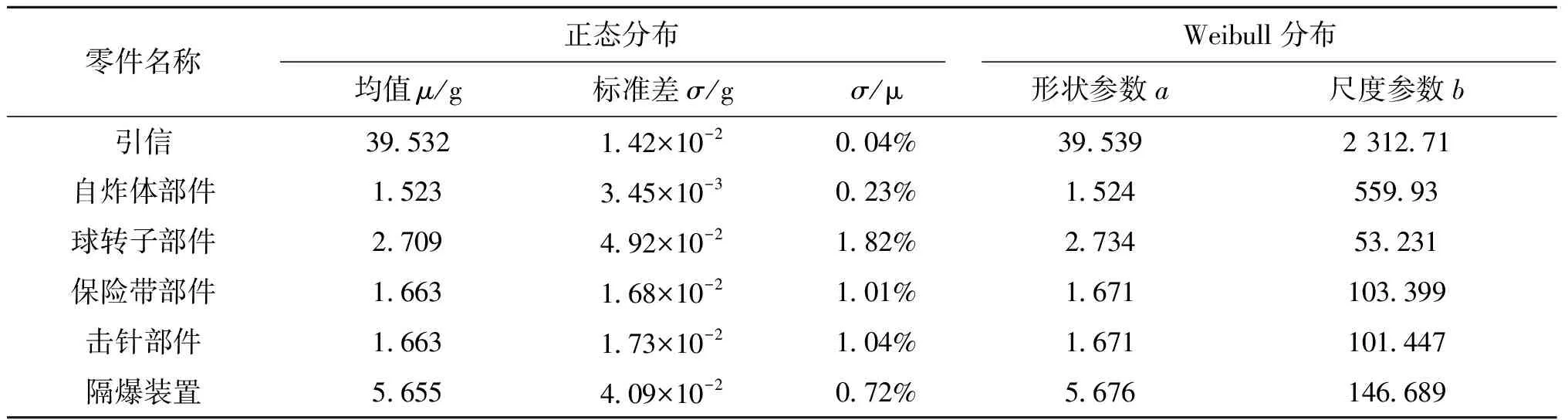
表5 各部件质量散布参数

表6 各部件特征和散布拟合检验结果

表1和表3中簧圈和垫片两种零件质量散布较大，簧圈可达±17.5%，垫片可达±28.9%。分析发现其原因分别是：簧圈主要尺寸公差相对值都比较大，如长度为±1.5%、厚度为±10%、宽度为±5%；垫片振动抛光磨去的厚度难以均匀因而散布很大，并且厚度公差相对值已达±6.1%。

由表4可看出，引信的18种机械零件中，自炸体、下体、垫片、开口环和套符合正态分布，压杆、球盖符合Weibull分布，支承杆既符合正态分布也符合Weibull分布。由表6可看出，除自炸体部件和球转子部件无明显分布特征外，其余部件都符合正态分布，且隔爆装置部件还符合Weibull分布；部件装配时微量添加物对部件分布特征无影响。

3 结果分析

为深入分析影响零件质量散布特性的因素，对文献[3]所涉及的23 mm口径高炮引信零进行进一步分析，零件特征和散布拟合检验结果如表7所列，其中平均尺寸精度等级及含义与表4的相同。

对影响某小口径航炮引信和23 mm口径高炮引信零件质量的因素进行统计分析，结果如表8所列。其中23 mm口径高炮引信零件中的保险销因质量太小(0.003 g)，测量仪器精度无法区分而无法得到分布类型，未计入统计中。

由表8的统计结果可以看出：

结构维数越多，零件的质量散布越大，服从正态分布和Weibull分布的零件数量比例也越大。结构维数为1的零件(钢球)质量没有明显的分布特性，结构维数为2和3的零件，质量散布特性服从典型散布的比例相近。

零件尺寸越多，零件质量就越符合正态分布或Weibull分布，分布特性越明显；零件尺寸数对质量散布影响不大。

小质量的零件质量相对散布大。质量小于0.2 g的零件质量散布最大；零件质量散布特性与零件质量关系不大。

密度小的材料加工的零件质量散布较小；材料密度对零件质量散布特性影响不大。

无表面处理的零件质量散布最大，钝化处理的零件质量散布特性最明显。

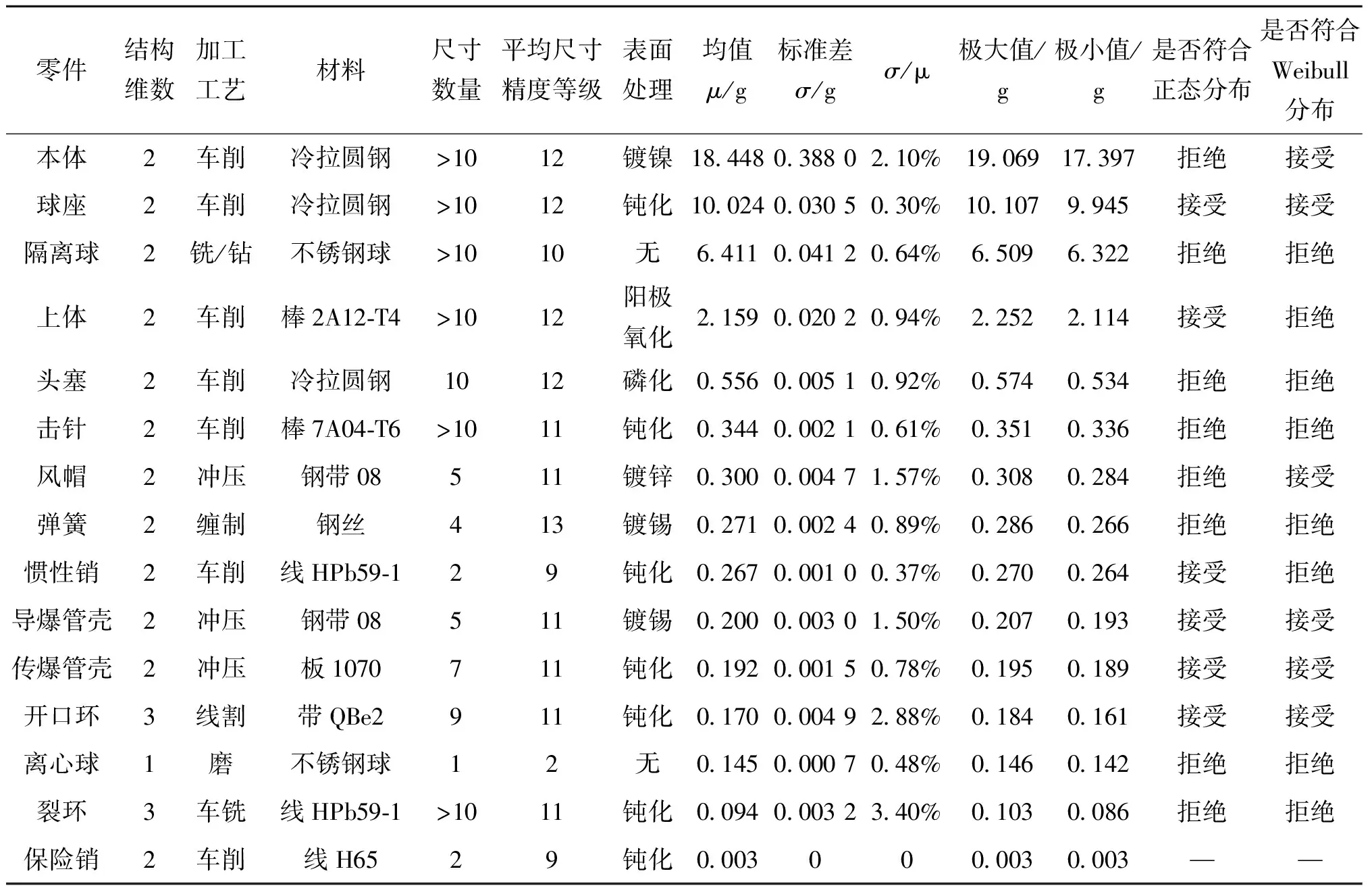
表7 参考文献[3]中零件质量均值、标准差、极值和散布拟合检验结果

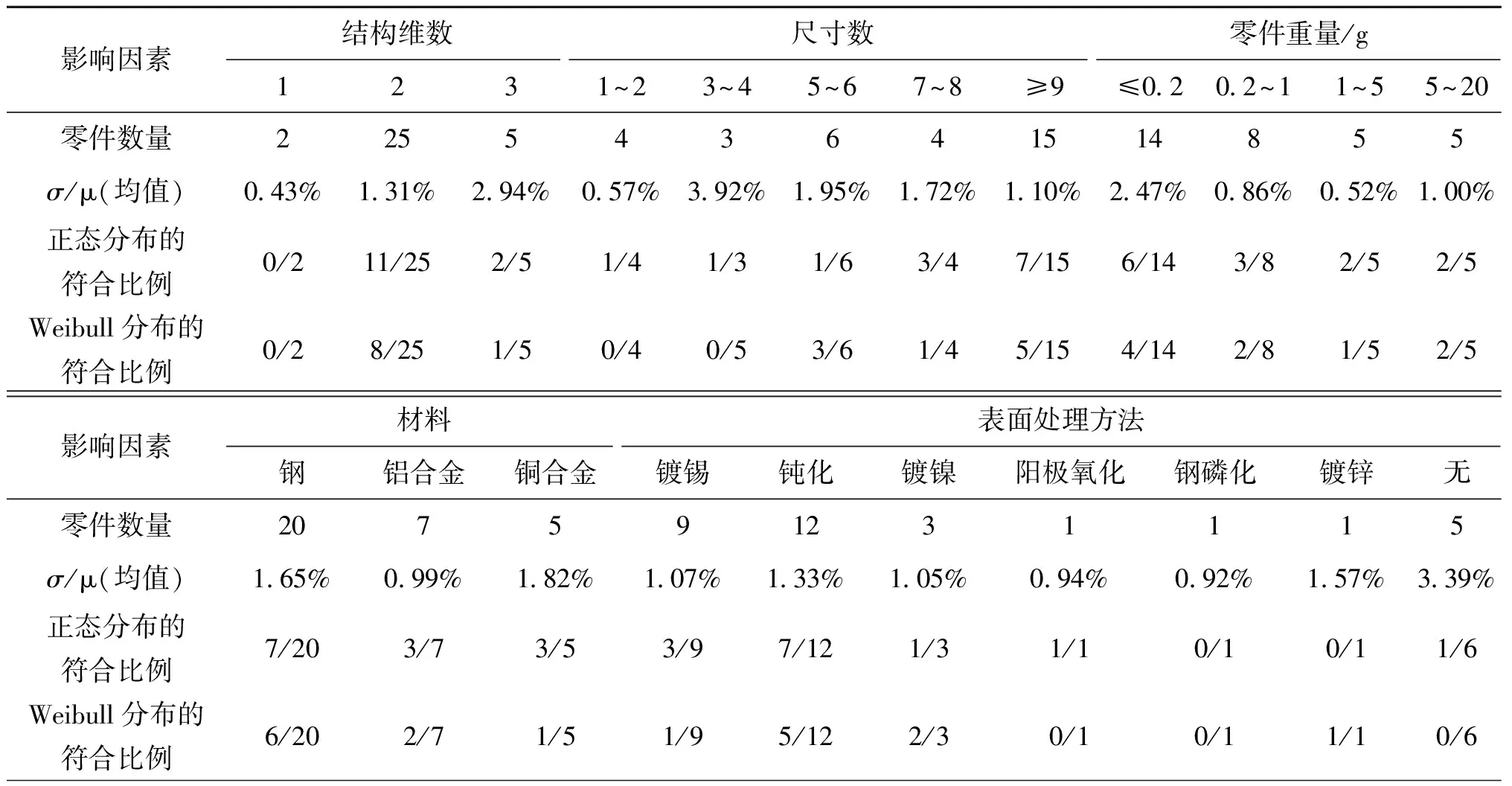
表8 两种小口径炮弹引信零件质量散布拟合检验结果

续表

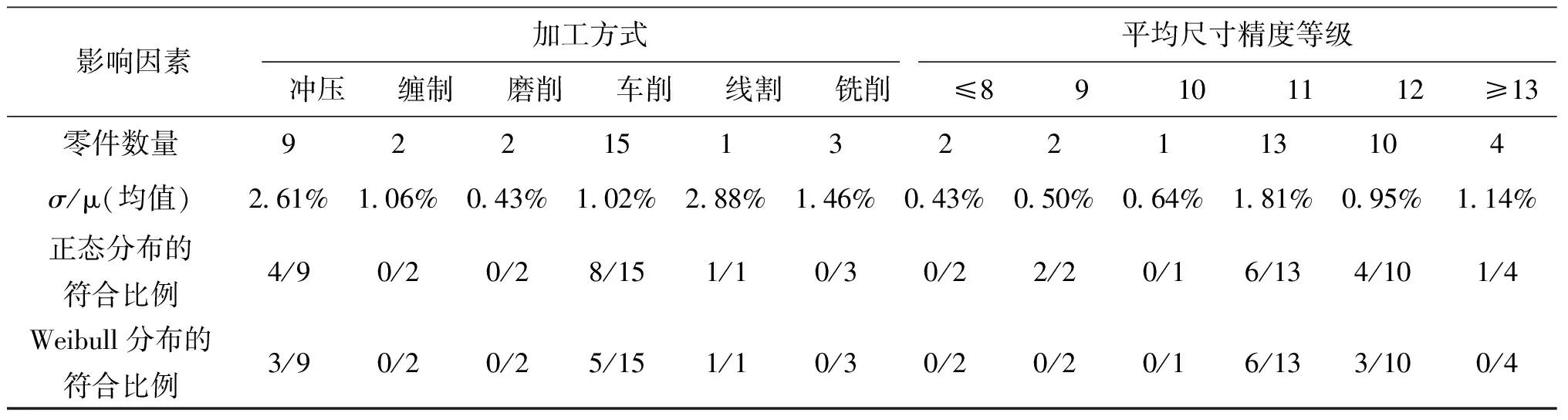
影响因素加工方式平均尺寸精度等级冲压缠制磨削车削线割铣削≤89101112≥13零件数量922151322113104σ/μ(均值)2 61%1 06%0 43%1 02%2 88%1 46%0 43%0 50%0 64%1 81%0 95%1 14%正态分布的符合比例4/90/20/28/151/10/30/22/20/16/134/101/4Weibull分布的符合比例3/90/20/25/151/10/30/20/20/16/133/100/4

加工为缠制(弹簧)、磨(保险球)和铣(隔离球)的零件质量无明显分布特性，而车削与冲压零件质量散布特性比较明显，约有二分之一的零件数量服从正态分布，约有三分之一的零件数量服从Weibull分布。

平均尺寸精度等级对质量散布有影响，对表8中平均尺寸精度等级和σ/μ(均值)进行线性拟合，利用最小二乘法得到的回归曲线方程为：

y=0.1455x-0.7825

式中，x为平均尺寸精度等级，y为σ/μ(均值，%)。

表8表明，平均尺寸精度等级为10级时其质量散布(3σ/μ)约为2%，11级时约为2.5%，12级时约为3%，大约每降低一个等级，零件质量散布约增大0.5%。平均尺寸精度等级对零件散布特性影响不明显。

4 结论

本文以一种小口径航炮弹头触发引信和一种高炮弹头触发引信为样本，利用数理统计方法获得了其机械零件质量散布特性。这两种引信零件质量总的散布特性规律相近；约有半数品种的零件质量散布服从正态分布或Weibull分布；还有约50%的零件种类不服从典型分布；结构维数越多，零件的质量散布越大；无表面处理的零件质量散布较大；平均尺寸精度等级为10级时其质量散布(3σ/μ)约为2%，11级时约为2.5%，12级时约为3%，每降低一个等级，零件质量散布约增大0.5%；平均尺寸精度等级对零件散布特性影响不明显。

文献[3]涉及的引信零件为设计阶段试验样品零件，多由数控机床或加工中心加工。本文涉及的引信零件为已生产定型多年、现处于大批量生产阶段的零件，多由普通机床加工。但针对这两种引信的研究结论并无矛盾之处，说明引信零件质量散布特性规律是相近或相同的。

[1]安晓红. 引信设计与应用[M]. 北京：国防工业出版社, 2006.

[2]张崇甫. 统计分析方法及其应用[M]. 重庆：重庆大学出版社, 1995.

[3]王晓鹏，王雨时，闻泉，等. 某高炮弹头触发引信机械零件质量分布特性[J]. 四川兵工学报，2015，36(5)：63-68.

[4]郭荣化, 李勇. 小样本试验中验前数据与现场数据相容性检验方法研究[C]//第13届中国系统仿真技术及其应用学术年会论文集.合肥：中国自动化学会系统仿真专业委员会, 2011.

[5]王晓鹏，王雨时，卢凤生，等.155mm口径火炮榴弹结构特征数分布特性研究[J].探测与控制学报, 2015,37(5):66-72.

[6]宋昕, 蔡泳, 徐刚,等. 非参数检验方法概述[J]. 上海口腔医学, 2004, 13(6):561-563.

[7]王岩. 数理统计与MATLAB工程数据分析[M]. 北京：清华大学出版社, 2006.

[8]刘海波，江健. 基于MATLAB的某型挖掘机可靠性分布模型辨识[J]. 工程机械，2014，45(10):18-23.

The Mass Distribution of Mechanical Components of Small Caliber Artillery’s Point Detonating Fuze

LIU Peng, WANG Yushi, WEN Quan, ZHANG Zhibiao

(Mechanical Engineering School, NUST, Nanjing 210094，China)

In order to find the mass distribution regularity of fuze’s mechanical components,thereby improving product engineering quality, security and reliability of fuze, according to the point detonating fuze of a small caliber aircraft gun and antiaircraft gun, the mass distributions of the components were gained with the method of mathematical statistics.The mass distribution regularity of fuze’s components is similar or same. More than half of the components’ mass obey normal distribution or weibull distribution. There are about half kind of the component are not subject to typical distribution. The more components structure dimension are, the greater the mass spread.Components without surface treatment have greater mass spread. The mass spread (3σ/μ) is about 2% when the average of the dimensional accuracy class at 10, 2.5% at 11 and 3% at 12, the average of the dimensional accuracy class decreasing by a grade,the mass spread of components increased about 0.5%. The average of the dimensional accuracy class has little effect on the mass distribution of components.

fuze; mathematical statistics; components mass; distribution

2016-08-21

武器装备预先研究项目资助(51305060301)；江苏省自然科学基金青年基金项目资助(BK20140786)

刘鹏(1991—)，男，湖南长沙人，硕士研究生，研究方向:引信及弹药总体技术。E-mail：skiy906@163.com。

TJ430.8

A

1008-1194(2017)03-0017-07