基于多普勒频差曲线特征识别的炸点控制方法
2017-07-12武雄飞郭东敏权建峰
武雄飞,郭东敏,权建峰
(机电动态控制重点实验室,陕西 西安 710065)
基于多普勒频差曲线特征识别的炸点控制方法
武雄飞,郭东敏,权建峰
(机电动态控制重点实验室,陕西 西安 710065)
针对短时傅里叶变换在分析对空无线电引信目标多普勒信号频谱特征时频率分辨率不足的问题,提出基于多普勒频差曲线特征识别的炸点控制方法。该方法对多普勒信号进行短时傅里叶变换与离散时间傅里叶变换结合的时频分析,提取出多普勒频差曲线,并识别出曲线跳变点作为特征信号进行炸点精确控制。实测信号的仿真表明,该算法比短时傅里叶变换算法提取的频率更加精确,反应出更丰富的弹目交会信息,可有效提高引信精确炸点控制性能,有一定实用价值。
多普勒信号;短时傅里叶变换;离散时间傅里叶变换;炸点控制
0 引言
连续波多普勒体制无线电引信一般利用目标回波信号幅度、增幅速率、多普勒频率和多普勒频率的变化率等信息作为炸点控制的判定依据,受目标特征信息模糊影响可能出现目标误判、弹道早炸等现象。当目标处于近场区,可视为由若干主散射点构成,其多普勒信号不再是单一的频率,而是会呈现出多分量,提取具有多分量的多普勒频率可为炸点控制提供更充分的依据。由于弹目交会过程中脱靶量一般不为零,防空反导炮弹主要依靠战斗部在炸点位置作用后飞散出的破片来提高毁伤概率,采用定角起爆的方式可获得很高的毁伤概率[1]。
引信回波信号是典型的非平稳信号,常用的分析非平稳信号方法有短时傅里叶变换(STFT)、魏格纳分布(WVD)、伽伯变换和小波变换(WT)、希尔伯特-黄变换(HHT)等。WVD在处理多分量信号时存在交叉项干扰[2],伽伯变换和小波变换运算量较大,HHT在处理多分量信号时经验模态分解(EMD)会出现伪分量[3]。为满足系统实时性需求,工程上多采用STFT来处理多普勒信号。STFT通过时域加窗将信号分成若干段,在每段信号近似平稳的前提下进行傅里叶变换获取频谱[4]。
由于对空无线电引信与目标相对速度较快,目标多普勒信号的伪平稳长度较短,STFT算法的频率分辨率不足以准确识别出多分量。本文针对此问题,提出了基于多普勒频差曲线特征识别的炸点控制算法。
1 连续波多普勒引信信号频谱分析方法
1.1 基于STFT多普勒信号时频分析的炸点控制
连续波多普勒体制引信采用STFT算法对多普勒信号进行时频分析,根据回波信号中多普勒信号的能量及频率特征进行目标识别和炸点控制[5],STFT在对各段数据进行傅里叶变换时通常采用DFT,基于STFT多普勒信号时频分析的炸点控制方法原理框图如图1所示。
判定准则为:当回波能量高于判别门限,认为发现目标;当多普勒频率下降到判别门限以下即输出起爆信号。
1.2 基于离散时间傅里叶变换的频谱细化算法
离散时间傅里叶变换(DTFT)是信号处理中的一个重要理论[6],其时域是离散的,而频谱是连续的,DTFT谱是关于频率的连续函数,利用其连续性可以得到任意小频域范围内的局部频谱,突破了离散傅里叶变换(DFT)频谱只存在于基频整数倍的限制。DTFT频谱的连续性对应时间无限长的采样序列,而工程应用中采样序列为有限长度,因此无法直接利用DTFT公式进行计算,对此,文献[7]提出了改进的DFT算法(即近似DTFT算法),对于短信号和瞬态信号的频率细化具有显著效果。
该算法首先根据实际需要,确定细化频率区间[f1,f2]和所需频率步进量Δf,计算频率序列为[f1,f1+Δf,f1+2Δf,…,f2],循环计算各频点的值,对多普勒信号进行局部频域分析,可获得比DFT更精细的频谱。
2 基于多普勒频差曲线特征识别的炸点控制算法
2.1 基于STFT-DTFT的时频分析
弹目交会过程中,目标多普勒信号在远场区频率随时间下降较慢,随着弹目距离减小,多普勒频率急剧下降,并且呈现出多分量的趋势,这是因为目标具有强散射特性的部位是离散的(比如飞鱼导弹具有强散射特性的主要是头部、侧翼和尾翼等部位),目标各主散射部位与引信的相对速度不同,在频谱中对应不同的谱峰。
由于信号的非平稳性,STFT算法难以兼顾信号平稳性与频率分辨率。DTFT可在不增加数据长度的前提下提高频率分辨率,本文将其与STFT结合使用,称为短时傅里叶变换与离散时间傅里叶变换结合的算法,简称STFT-DTFT,可保证信号近似平稳性的同时达到区分不同主散射点对应谱峰的频率分辨率。
STFT-DTFT由采样率和系统实时性要求确定时域窗函数长度,先用DFT算法作全景谱确定DTFT的细化频率区间,再由交会过程中弹目距离减小与频率下降的对应关系确定所需频率步进量。确定参数后进行时频分析,得到精细化频谱。原理框图如图2所示。
2.2 基于多普勒频差曲线特征识别的炸点控制算法
基于多普勒频差曲线特征识别的炸点控制算法以目标回波多普勒信号为输入,经过STFT-DTFT处理和多普勒频差曲线特征识别后,输出起爆信号。原理框图如图3所示。
提取频差曲线:精细化频谱可对多普勒频率多分量做出识别,体现在频谱上的两到三个谱峰,提取出谱峰间隔随时间的变化曲线即为多普勒频差曲线。宽波束天线可同时探测到两至三个主散射点,第一个主散射点和第三个主散射点同时在波束角内的情况只存在于第一个散射点即将移出波束角之前很短的时间内,且此时第三个主散射点的回波信号能量较弱,因此提取出的频差曲线对应前两个主散射点。
弹目平行交会条件下,脱靶量为1.5 m的暗室实测信号多普勒频差曲线如图4所示。
曲线跳变识别:在弹目交会过程中,目标回波信号多普勒频率持续下降,且随着弹目距离减小下降速度变快,因此提取的频差曲线呈现出增长的趋势,直至第一个主散射点移出天线波束角范围(对应弹目距离为2~3 m),天线接收到第一个主散射点的回波能量衰减,频差曲线出现跳变,系统输出起爆信号。
3 仿真验证
3.1 STFT-DTFT参数确定
确定细化频率区间:对空目标为导弹,弹目交会过程中多普勒信号频率存在于最大多普勒频偏f至0的频率范围内。在Matlab环境下,通过STFT得到实测多普勒信号s0在目标远场区的频谱如图5和图6所示。

确定频率步进量:以平行交会为例,弹目相对速度为vr=1 000m/s,脱靶量为3.5m,弹目距离R为8m时,R减小0.5m对应着多普勒频率下降约为2kHz,因此选择DTFT频率间隔为1kHz。
3.2DTFT频谱细化算法仿真
在Matlab环境下,选取脱靶量分别为1.5m、2.5m和3.5m的连续波多普勒体制无线电引信实测多普勒信号s1、s2和s3。用DTFT算法对目标暗室实测信号进行频谱分析,并将结果与DFT算法进行比较。选取s1上以弹目距离5.2m处为起点记录的512点信号、s2上以弹目距离8.5m处为起点记录的512点信号,s3上以弹目距离9.5m处为起点记录的512点信号进行分析。图7、图9和图11的上图分别表示s1、s2和s3的完整信号波形,下图表示进行频谱分析的三段信号波形。图8、图10和图12分别表示三段信号DTFT和DFT频谱分析的结果对比。
从图7和图8可以看出,s1在弹目距离5.2 m处的DFT谱图中存在一个谱峰,表示DFT算法在5.2 m处分辨出一个强散射点。在0~230 kHz的频率区间用DTFT以1 kHz频率间隔分析得到两个谱峰,谱峰间隔5 kHz,表示DTFT算法在5.2 m处分辨出两个强散射点,且对应的多普勒频率差为5 kHz。
从图9和图10可以看出,s2在弹目距离8.5 m处的DFT谱图中存在一个谱峰,表示DFT算法在8.5 m处分辨出一个强散射点。在0~230 kHz的频率区间用DTFT以1 kHz频率间隔分析得到两个谱峰,谱峰间隔为4.5 kHz,表示DTFT算法在8.5 m处分辨出两个强散射点,且对应的多普勒频率差为4.5 kHz。
从图11和图12可以看出,s3在弹目距离9.5 m处的DFT谱图中存在一个谱峰,表示DFT算法在9.5 m处分辨出一个强散射点。在0~230 kHz的频率区间用DTFT以1 kHz频率间隔分析得到两个谱峰,谱峰间隔为5 kHz,表示DTFT算法在9.5 m处分辨出两个强散射点,且对应的多普勒频率差为5 kHz。
由以上仿真结果可知,当谱峰间隔介于1~7 kHz之间,即多普勒频率差在DFT算法频率分辨率和DTFT算法频率分辨率之间时,前者无法对两个谱峰做出识别,而DTFT算法通过更精确的频谱细节反应出目标在近场区的体效应,时域加窗后以DTFT算法在时间轴上连续进行谱分析,得到精细化时频分析图,提取时频图中多分量多普勒频率曲线之间的频率差,可得到多普勒频差随时间变化的曲线。
3.3 基于频差曲线特征识别的炸点控制算法仿真
由3.2节分析可知,DTFT频谱细化算法可对体目标回波信号多普勒频率多分量进行识别。根据STFT-DTFT算法得到精细化时频分析图后进行谱峰识别,提取出多普勒频差(即谱峰间隔)曲线,信号s1多普勒频差曲线和输出结果如图13、图14所示。
信号s2频差曲线和输出结果如图15、图16所示。
信号s3频差曲线和输出结果如图17、图18所示。
从图13、图15和图17可以看出多普勒频差曲线总体呈上升趋势,并在上升过程中出现跳变,对此跳变进行检测识别并输出起爆信号,起爆时弹目距离为2.23 m、3.53 m和4.55 m,如图14、图16和图18所示。
常规炮弹通过爆炸或解体,用其自身携带的预制破片或壳体破碎形成的自然破片毁伤目标,毁伤效果与破片大小、形状、初速、弹目相对速度和破片飞散角等因素有关。炮弹破片初速约为1 200~1 400 m/s,由于破片有效杀伤距离相对不大,故可忽略破片在空气中的速度衰减;炮弹破片飞散方向与战斗部纵轴的夹角小于10°,可认为静态爆炸时破片飞散方向垂直于弹轴且具有轴向对称性;在炮弹有效毁伤距离范围内,其速度在930~600 m/s之间,飞鱼导弹速度约为300 m/s,故平行交会条件下,弹目相对速度介于1 230~900 m/s之间。
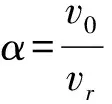
信号s1、s2和s3的起爆角分别为42°、45°和50°,符合上述范围。
3.4 算法仿真结果统计
对脱靶量分别为1 m、1.5 m、2 m、2.5 m、3 m和3.5 m的实测信号加入白噪声进行100次蒙特卡洛实验,起爆角满足40°~60°则认为实现了定角起爆,分别统计以幅-频特征为判据的炸点控制方法和以多普勒频差曲线特征为判据的炸点控制方法,起爆角满足40°~60°之间的概率统计结果如表1所示。
从统计结果可以看出,相比较以幅-频特征为判据的炸点控制方法而言,基于多普勒频差曲线特征识别的炸点控制方法在不同脱靶量下均能更好地满足定角起爆,进一步提高了引战配合效率。
4 结论
本文提出了基于多普勒频差曲线特征识别的炸点控制算法,该算法先通过短时快速傅里叶变换确定多普勒信号的频带范围,对此频率范围进行STFT-DTFT(短时傅里叶变换与离散时间傅里叶变换结合)的时频分析,获得更精细的频谱,根据精细化频谱提取出多普勒频差曲线,对曲线跳变点进行识别,最后输出起爆信号。Matlab仿真结果表明,STFT-DTFT算法比短时快速傅里叶变换算法提取的频率更加精确,提取出多普勒频差跳变点作为特征信号可作为炸点精确控制的判定依据,在工程实践中有一定应用价值。
[1]胡照. 炮弹新型战斗部技术发展概况[J]. 中国城市经济,2010(5):18-19.
[2]罗利春. 用维格纳-威利时频分布进行信号时频分析[J]. 航天电子对抗,2003(4):18-21.
[3]LI Y J,TSE P W,YANG X, et al. EMD-based fault diagnosis for abnormal clearance between contacting components in a diesel engine[J]. Mechanical Systems and Signal Processing,2010(24):193-210.
[4]权建峰,郭东敏. 基于小波变换的频率捷变引信信号分析[J].探测与控制学报,2005,27(1):13-15.
[5]罗德宏,孙永泽,郭东敏,权建峰. 模块化的连续波多普勒引信信号处理仿真平台[J]. 探测与控制学报, 2014,36(3):60-68.
[6]肖玮,涂亚庆,何丽. DTFT频谱细化特性分析及其快速算法设计[J]. 电子与信息学报, 2011,33(6):1395-1400.
[7]刘进明,应怀樵. FFT谱连续细化分析的富里叶变换法[J]. 振动工程学报,1995,8(2):162-166.
Detonating Control Based on Characteristics of Doppler Frequency Difference Curve
WU Xiongfei,GUO Dongmin,QUAN Jianfeng
(Science and Technology on Electromechanical Dynamic Control Laboratory,Xi’an,710065,China)
For the problem of short-time Fourier transform that frequency resolution is insufficient when analyzing the spectrum characteristics of Doppler signal of anti-aircraft radio fuze target, a detonating control method based on Doppler frequency difference curve characteristics identification was proposed. By means of Time-Frequency Analysis based on short-time Fourier transform and discrete-time Fourier transform of Doppler signal, the method extracted the Doppler frequency difference curves and identified the curve discontinuity as the characteristic for accurate detonate control. The simulation showed that the proposed algorithm was more accurate than short-time Fourier transform and contained more rendezvous information, which could effectively improve the detonating control performance.
doppler signal; short-time fourier transform; discrete-time fourier transform; detonating control
2017-02-12
武雄飞(1991—),男,陕西富平人,硕士研究生,研究方向:快速实时数字信号处理。E-mail:393832503@qq.com。
TJ434.1
A
1008-1194(2017)03-0081-05
