基于多维临界调控模型的玛纳斯河流域水资源调控

杨明杰，杨广，何新林，龙爱华,2，陈江春，王翠，李小龙

（1石河子大学水利建筑工程学院/现代节水灌溉兵团重点实验室，新疆 石河子 832003；2中国水利水电科学研究院水资源研究所，北京 100044）

基于多维临界调控模型的玛纳斯河流域水资源调控

杨明杰1，杨广1，何新林1，龙爱华1,2，陈江春1，王翠1，李小龙1

（1石河子大学水利建筑工程学院/现代节水灌溉兵团重点实验室，新疆 石河子 832003；2中国水利水电科学研究院水资源研究所，北京 100044）

水资源调控是不同区域和用水户之间有效公平分配水资源的重要途径，本文以新疆玛纳斯河流域为研究对象，以水资源供需缺水量最小为优化目标，在分析耗散结构、协同学、有序原理和临界控制论的基础上，应用多维临界调控模型对玛纳斯河流域水资源系统进行行业间优化调控。研究结果表明：2020年，通过工业节水30.8%、农业节水1.2%和污水资源化1.38×108m3，可使系统熵由0.34降低到0.15；2030年，通过工业节水54%、农业节水1.6%和污水资源化1.89×108m3，可使系统熵由0.34降低到0.15；2030年的缺水量比2020年的缺水量减少了0.4×108m3，可实现水资源系统的有序发展。研究成果对解决灌区水资源供需矛盾、提高水资源高效利用具有重要意义。

玛纳斯河流域；多维临界调控；系统熵；有序发展；水资源高效利用

玛纳斯河流域位于天山北麓准噶尔盆地南缘，地处 N43°27′-N45°21′，E85°01′-E86°32′，远离海洋，气候干燥，是典型的大陆性干旱气候。随着人口的增长、经济的快速发展和水资源的长期开发利用，灌区的水资源供需矛盾愈发突出，严重制约了地区发展。为保证水资源的可持续发展，最大限度的满足供水要求，对玛纳斯河流域水资源配置就显得尤为重要[1]。

水资源配置是一个复杂的系统工程，涉及水资源、经济、社会、生态系统之间的协调。国外学者采用多目标规划理论、多用户交互式模型、地表水地下水再生水联合运用、水资源管理与GIS有机联动等[2-5]；国内学者采用“人工-自然”二元水循环、全属性功能水资源配置、水资源全要素配置模型、基于ET的水资源合理配置等[6-9]，对如何提高水资源、经济、社会、生态之间的协调度进行了大量研究。

相互依存相互制约的子系统决定复杂巨系统的运行方向，为保证水资源系统协调、有序和良性循环，需要研究水资源-经济-社会-生态的相互协调、水资源合理配置和系统崩溃临界阈值等问题。多维临界调控理论由临界控制论、有序原理、耗散结构理论和协同学等组成，可应用于水资源优化配置研究，对多个相互矛盾的目标进行科学分析，使复杂巨系统向协调和有序方向运行[10]。其含义有以下三层[10-12]：（1）协调。协调水资源、经济、社会、生态之间以及各用水部门之间的关系，使系统整体以及各个子系统都能充分发挥其最佳效应。（2）优化。优化是多维临界调控取得整体、协调、有序、高效的必要手段。（3）良性循环。良性循环是水资源系统维持可持续的最终目标。

为了均衡各灌区用水部门之间的用水量，本文针对玛纳斯河流域的石河子灌区、莫索湾灌区、下野地灌区的行业间用水问题，采用多维临界调控模型，提出了综合考虑水资源、经济、社会和生态四方面因素的水资源临界调控模型，可实现水资源系统的有序发展，对于解决灌区水资源供需矛盾、提高水资源高效利用具有重要意义。

1 水资源多维临界调控模型

多维临界调控的研究对象是自然和人文系统组成的复杂巨系统。水资源系统是“天然-人工”二元水循环的复杂巨系统[13]，水资源多维临界调控主要用于解决多目标、动态、不确定和群决策问题，通过工程和非工程措施，对水资源的开发利用过程进行调节和控制，以缓解水资源短缺的现状，逐步解决水资源供需矛盾，从而实现复杂巨系统有序发展。

1.1 水资源多维临界调控子系统有序度

水资源系统是耗散结构[14]，系统的相变结果不一定都走向新的有序，也可能走向无序 ，因此，为了把握系统协调的程度，引入有序度来衡量协同作用。考虑子系统SSi演化进程中的序参量变量为eij=（ei1，ei2，…，ein），其中 n≥1，eij的取值应在临界阈值区间，如：Ui≤eij≤Ti，j∈[1，n]。针对玛纳斯河灌区水资源系统给出如下有序度的计算，子系统序参分量eij的有序度为：

式中：ui（eij）为序参分量eij的有序度；Uij和Tij分别为eij的最小和最大临界阈值。

由式（1）可知，若序参量eij的有序度值ui（eij）∈[0，1]，则序参量在临界阈值区间，且其值越大，eij对子系统 SSi有序的“贡献”越大。相反，若 eij∈[0，1]，说明eij不在合理阈值区间，需进行调节。从总体上看，序参量变量eij对子系统SSi有序程度的“总贡献”可通过ui（eij）的集成实现，计算公式如下：

式（2）中，λj为序参量分量eij的权系数,ui（eij）为序参分量eij的有序度。

协同学认为系统内各子系统参量对系统的影响是有差异的、不平衡的，因此，把系统参量分为快变量和慢变量，慢变量决定着系统的演化进程，支配着快变量的行为[16]，协同学中把慢变量称为序参量。由于玛纳斯河流域水资源系统的复杂性和不确定性[17]，无法区分出序参量随时间变化的快慢程度，因此序参量的确定只能按照其代表的意义。经济子系统中衡量经济发展的指标包括人均GDP、GDP增长率、工业产值模数、人均粮食产量、工业总产值占GDP比重等，但其中任何一个值的变化都不能同时确定其他指标的变化趋势，即不能支配其他指标的行为。因此，经济子系统序参量的选择要从分析经济效益入手，水资源系统的经济效益主要是针对国民经济各部门的供水效益，包括农业灌溉用水效益和工业、生活供水效益，因此，经济子系统的序参量为生活、工业、农业供水量。经过分析，各子系统的序参量选取如表1所示。

表1 玛纳斯河流域水资源多维临界调控序参量Tab.1 Multi-dimension critical control order parameter of water resources in Manasi River Basin

1.2 水资源系统演化方向的定性推理

水资源系统是水资源、经济、社会和生态的复合系统，四个子系统相互联系、相互作用，某一个子系统有序度的变化，会引起其他子系统有序度变化，但整个系统的有序度如何从无序向有序变化，是水资源系统临界调控需要解决的问题。耗散结构的熵理论指利用熵减小有序性增强、熵增大有序性减弱的关系，对系统演化方向进行定性分析[11]。根据熵的含义，利用子系统有序度建立判别水资源系统演化方向的系统熵函数[11]：

式（3）中u1（e1）、u2（e2）、u3（e3）、u4（e4）分别代表水资源、经济、社会和生态子系统的有序度。

根据有序度与熵变理论，有如下定理：如果子系统有序度的变化Δui（ei）导致熵函数SY减少，那么整个系统的有序度将增加，表明各子系统能够协调发展，系统向有序或良性方向演化。反之，系统向无序或恶性方向演化。为此，得出以下判别公式[11]：式（4）中：SY（n+1）为系统第 n+1次调控后的末态熵，SY（n）为第n次调控后的熵，ΔSY为第n+1次调控引起的熵变。

根据熵ΔSY变值的大小，可判断系统演变方向。当连续调控所得ΔSY=0时，表明调控后系统熵无变化，系统状态熵收敛，实现寻优[11]。

2 实例计算及验证

2.1 基础数据求解

根据红山嘴水文站玛纳斯河日径流量数据（1956-2014年），运用水文频率分析法，选取75%保证率下径流量11.92×108m3为基准年的径流量，以此作为2020年和2030年的来水量对水资源进行优化配置。

各序参量的临界阈值是系统调控的基础，因此为了进行调控，各临界阈值应该通过知识获取的方法明确给出，包括供水量阈值、地下水开采量阈值、水库调度期末库容阈值、和非汛期生态基流阈值。阈值计算结果见表2。

表2 玛纳斯河流域序参分量阈值Tab.2 Threshold value of order parameter in Manasi River Basin

依据《石河子市城市总体规划》、《新疆水资源公报》等农八师水资源利用综合规划的相关基础数据，采用指标预测法预测玛纳斯河流域2020年和2030年需水量，各类用水户分为生活、工业、农业和生态四类。生活需水包括城镇居民生活需水和农村居民生活需水，采用人均日用水定额预测水量；工业需水包括工业生产需水、建筑业和第三产业需水，在预测各自经济指标的基础上采用万元增加产值取水量的方法进行预测；农业需水包括小麦、玉米、棉花、葡萄、苗果林、牧草等的需水，以及渔业、牲畜需水，按单位面积用水量（牲畜按头数）进行预测；生态需水包括河道外生态环境需水和河道内生态需水，河道外生态需水按单位面积用水量预测，河道内生态需水按不低于多年平均径流量的10%预测。需水量预测结果如表3所示。

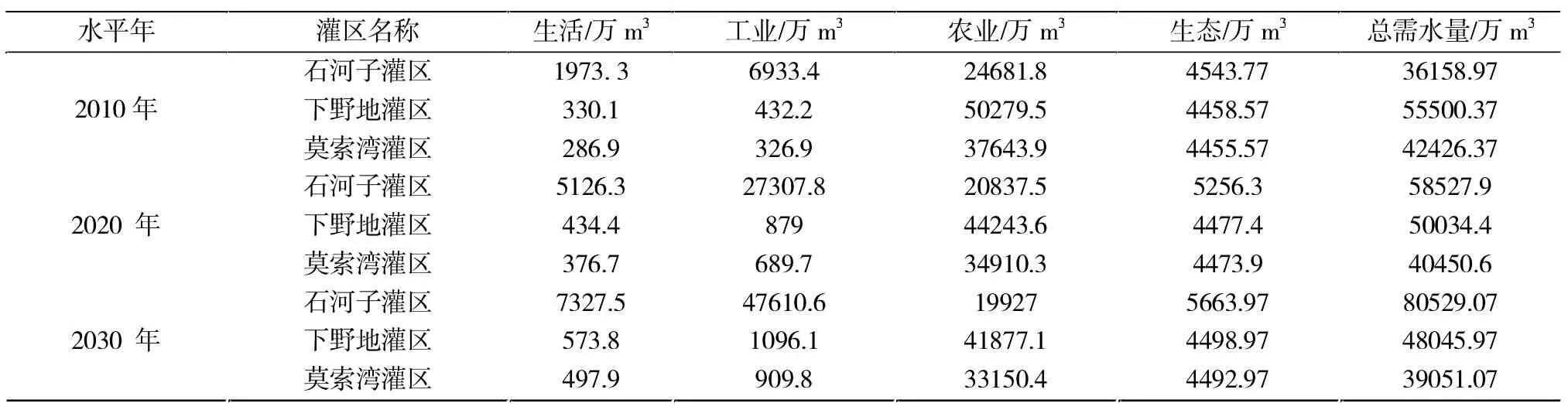
表3 玛纳斯河流域2010年、2020年和2030年需水量Tab.3 Water requirement of Manasi river basin in 2010,2020 and 2030

2.2 调控方案

现状年2010年需水量为13.38×108m3，规划水平年2020年需水量为14.9×108m3，2030年需水量为16.76×108m3，供需水矛盾进一步加剧，为解决水资源短缺，需运用调控手段：

（1）运用农业、工业适度节水调控手段将农业、工业需水预测值作为需水方案。

（2）根据《兵团第八师水中长期供求规划》，运用农业强化节水调控手段提高灌溉利用系数，降低毛灌溉定额，使农业强化节水的需水量相对于预测方案分别减少1.2%和1.6%，运用工业强化节水调控手段降低工业用水增长率、采取节水工艺、提高重复利用率等手段和措施，使工业需水量分别减少至30.8%和54%。

（3）改进污水处理工艺和技术，进一步提高城镇工业、生活污水资源化比例，力争在2010年污水资源化0.86×108m3的基础上，使2020年和2030年的污水资源化达到1.38×108m3和1.89×108m3。

2.3 模型验证

子系统的有序度和系统熵指引水资源配置是玛纳斯河流域水资源多维临界调控的核心。在有序度和系统熵的指引下，水资源被配置到对系统熵贡献值最大的子系统中，使系统熵沿着熵变梯度最大的方向逐渐减小，直至收敛，从而使玛纳斯河流域各子系统之间的协调度最大。2010年，初始调控时系统内各子系统之间协调程度相对较差，需进行调节，通过污水资源化0.86×108m3，并伴随调控措施，水资源子系统、经济子系统、社会子系统和生态子系统之间更加协调，使系统熵由0.34降低到0.15，表明所采取的调控措施使各子系统之间的协调性加强，其系统熵收敛趋势图如图1所示。

由2010年现有的水资源配置方案求得的系统熵为0.32，大于多维临界调控求得的系统熵0.15。由此可知，水资源多维临界调控对水资源配置具有优化作用，对维持水资源系统的可持续发展具有重要的意义。

图1 2010年水资源系统熵收敛趋势图Fig.1 Trend of entropy convergence of water resources system in 2010

3 基于多维临界调控的玛纳斯河流域水资源调控的结果与分析

3.1 结果

以2020年初始方案（方案一）为例，初始调控时系统内各子系统之间协调程度相对较差，且经济子系统下农业供水序参量及工业供水序参量均为负数，即[0，1]，说明不在合理阈值区间，需进行调节。通过污水资源化1.38×108m3，工业节水30.8%和农业节水1.2%，并伴随调控措施，水资源子系统、经济子系统、社会子系统和生态子系统之间更加协调。使系统熵由0.34降低到0.15，表明所采取的调控措施使各子系统之间的协调性加强。调控过程系统熵收敛趋势图如图2所示。2030年，通过污水资源化1.89×108m3，工业节水54%，农业节水1.6%，并伴随调控措施，使得水资源系统的系统熵由0.34降低到0.15。其调控过程的系统熵收敛趋势图如图3所示。

图2 2020年水资源系统熵收敛趋势图Fig.2 Trend of entropy convergence of water resources system in 2020

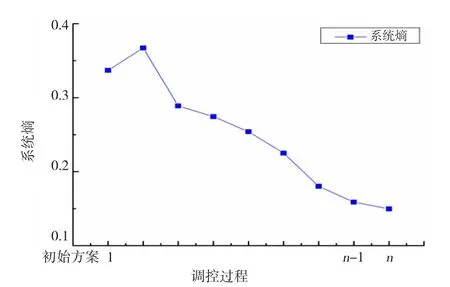
图3 2030年水资源系统熵收敛趋势图Fig.3 Trend of entropy convergence of water resources system in 2030

按照相应的调控措施，对2020年和2030年玛纳斯河灌区水资源系统进行多维临界调控，其结果如图4、图5所示。

图4 2020年水资源多维临界调控结果Fig.4 Multi-dimension critical adjustment of water resources in 2020

图5 2030年水资源多维临界调控结果Fig.5 Multi-dimension critical adjustment of water resources in 2030

图6 调控结果对比Fig.6 Comparison of adjustment results

3.2 分析

多维临界调控模型将水资源系统划分为四个子系统进行调控，生活供水0.59×108m3，工业和农业供水 9.77×108m3，生态供水 1.42×108m3，使得2020年水资源系统熵由最初的0.34降低到0.15，使缺水量由初始方案的3.12×108m3降低到0.75×108m3，调控效果较为明显。通过相应的水资源调控措施，使得2030年水资源系统熵由初始方案的0.34降低到0.15，缺水量由初始方案的4.98×108m3降低到0.29×108m3。调控结果显示：2030年的缺水量比2020年的缺水量减少了0.46×108m3，说明水资源系统向着有序协调的方向发展。

多维临界调控模型和交互式多目标决策方法均是将多目标决策系统转化为单目标决策系统，进而实现系统各单项目标间的总体协调控制。交互式多目标决策方法目标函数中仅包含社会效益、经济效益和生态效益，且在水资源配置中仅涉及到社会经济、水资源和生态的协调性，没有考虑到水资源开发利用存在着临界状态。交互式多目标决策方法和多维临界调控模型的水资源配置结果中，均满足了生活需水和生态需水，工业需水和农业需水均供应不足，其结果如图6所示。

多维临界调控结果相对于交互式多目标决策方法总供水量减少0.63×108m3，工业供水量减少0.43×108m3，农业供水量减少 0.2×108m3。在水资源配置中不仅要考虑到地表水源、地下水源和泉水的最大供水能力，还要将水资源循环的再生性维持在临界状态内，保证水资源系统的有序发展和生态系统的稳定。交互式多目标决策方法调控结果中，地下水超采，求得的系统熵无意义，系统向无序的方向发展，而多维临界调控所得系统熵为0.15，对维持水资源系统的有序协调发展具有重要意义。

4 结论

（1）玛纳斯河流域经济子系统与水资源子系统成正相关，生态子系统与经济子系统呈负相关；经济子系统和水资源子系统与系统熵呈负相关，生态子系统与系统熵呈正相关，且改变相同的系统熵，经济子系统较生态子系统变幅更大。

（2）2020年和2030年，玛纳斯河流域水资源系统的有序度由0.34降低到0.15，表明玛纳斯河流域各子系统之间协调度最好，水资源系统向有序协调的方向发展，进而保证水资源的可持续发展，顺应了“十八大”提出加强生态文明建设的要求下，首先应保证生活和生态需水。

（3）多维临界调控模型对解决玛纳斯河流域水资源供需矛盾、提高水资源高效利用具有重要意义，为解决复杂水资源系统的优化配置提供了新的思路，是一种解决流域子系统之间协调度的重要方法。

[1] Niu G，Li Y P，Huang G H，et al.Crop planning and Water Resource Allocation for Sustainable Development of an Irrigation Region in China under Multiple Uncertainties[J].Agricultural Water Management，2016，166:53-69.

[2] Zhao X S，Liu J.Multi-objective Optimal Allocation of Water Resources in Tianjin[J].Water Conservancy Science&Technology&Economy，2010，63(3):149-176.

[3] Kazimierz A S，Daniel P L.Interactive Simulation for Planning，Managing，and Negotiating[J].Closing the Gap Between Theeory and Practice，IAHS publ，1989(180):263-268.

[4] Carlos P，Gideon O，Abraham M.Optimal Operation of Regional System with Diverse Water Quality Sources[J].Journal of Water Resources Planning&Management，2014，123(2):105-115.

[5] Daene C M，Cai X M.Linking GIS and Water Resources Management Models:an Object-oriented Method[J].Environmental Modelling&Software，2002，17(5):413-425.

[6] 蒋晓辉.自然-人工二元模式下河川径流变化规律和合理描述方法研究[D].西安:西安理工大学，2002：22-23.

[7] 赵勇，裴源生，于福亮.黑河流域水资源实时调度系统[J].水利学报，2006，37(1):82-88.Zhao Y，Pei Y S，Yu F L.Real-time Dispatch System for Heihe River Basin Water Resources[J].Shui Li Xue Bao，2006，37(1):82-88.

[8] 康爱卿，魏传江，谢新民，等.水资源全要素配置框架下的三次平衡分析理论研究与应用[J].中国水利水电科学研究院学报，2011，9(3):161-167.Kang A Q，Wei C J，Xie X M，et al.Research and Application on Three Equilibrium Law under the Framework of Water Resources Entire Elements Option Allocation[J].Journal of China Institute of Water Resources and Hydropower Research，2011，9(3):161-167.

[9] 蒋云钟，赵红莉，甘治国，等.基于蒸腾蒸发量指标的水资源合理配置方法[J].水利学报，2008，39(6):720-725.Jiang Y Z，Zhao H L，Gan Z G，et al.Method for Reasonable Deployment of Water Resources Based on Evaportranspiration Index[J].Shui Li Xue Bao，2008，39(6):720-725.

[10] 姜秋香，付强，朱长虹，等.基于多维临界调控理论的水资源优化配置研究进展[J].东北农业大学学报，2015，46(7):103-108.Jiang Q X，Fu Q，Zhu C H，et al.Research Progress of Water Resources Optimal Allocation Based on Theory of Multidimensional Critical Regulation and Control[J].Journal of Northeast Agricultural University，2015，46(7):103-108.

[11] 彭少明，黄强，畅建霞，等.基于多维临界调控理论求解21世纪黄河水资源问题[J].水电能源科学，2005，23(1):18-21.Peng S M，Huang Q，Chang J X，et al.Solution of Water Resources in the Yellow River in Twentyfirst Century Ba-Based on the Theory of Multi Dimension Critical Control[J].Water Resources and Power，2005，23(1):18-21.

[12]甘泓，汪林，曹寅白，等.海河流域水循环多维整体调控模式与阈值[J].科学通报,2013,(12):1085-1100.Gan H,Wang L,Cao Y B,et al.Multid Imensional Integrated Control Model and Threshold of Water Cycle in the Haihe River Basin[J].Chinese Science Bulletin,2013,(12):1085-1100.

[13] 秦大庸，陆垂裕，刘家宏，等.流域“自然-社会”二元水循环理论框架[J].科学通报，2014，59(Z1):419-427.Qin D Y，Lu C Y，Liu J H，et al.Theoretical Framework of Dualistic Naturesocial Water Cycle[J].Chinese Science Bulletin，2014，59(Z1):419-427.

[14] 畅建霞，黄强，王义民，等.基于耗散结构理论和灰色关联熵的水资源系统演化方向判别模型研究[J].水利学报，2002，33(11):107-112.Chang J X，Huang Q，Wang Y M，et al.Water Resources Evolution Direction Distinguishing Model Based on Dissipative Structure Theory and Gray Relational Entropy[J].Shui Li Xue Bao，2002，33(11):107-112.

[15] 彭少明，信劲松，黄强，等.黄河流域水资源多维临界调控理论与模型研究[J].水利水电科技进展，2005，25(1):9-11.Peng S M，Xin J S，Huang Q，et al.Study on Theory and Model of MultidimEnsional Critical Regulation and Control of Yellow River Basin Water Resources[J].Advances in Sciience and Technology of Water Resources，2005，25(1):9-11.

[16] 翟慎良.重视改革的“慢变量”[J].领导科学，2015(27):1-1.Zhai S L.Pay attention to the Reform of"Slow Variable"[J].Leadership Science，2015(27):1-1.

[17] 张磊.不确定条件下的水资源系统优化模型研究[D].哈尔滨:东北农业大学，2015:4-5.

Adjustment of water resources in Manasi River Basin based on multi-dimension critical adjustment model

Yang Mingjie1，Yang Guang1，He Xinlin1，Long Aihua1,2，Chen Jiangchun1，Wang Cui1，Li Xiaolong1
(1 College of Water&Architectural Engineering/Key Laboratory of Modern Water-Saving Irrigation of,Xinjiang Production&Construction Group,Shihezi University,Shihezi,Xinjiang 832003 China;2 China Institute of Water Resources and Hydro Power Research,Beijing 100044,China)

Regulation of water resources is an important way in different regions and among water users effective and equitable distribution of water resources.In this paper,the research object is the Manas River Basin in Xinjiang and the optimization goal is the minimum water shortage of supply and demand.The optimal regulation of water resources system is analyzed by using the multi-dimension critical adjustment model based on the analysis of dissipative structure,synergetic theory and critical control theory in Manas River Basin.The results show that 30.8%of the industrial water saving,1.2%of agricultural water saving and 138 million cubic meters of waste water resources can make the system entropy reduced from 0.34 to 0.15 in 2020.54%of the industrial water saving,1.6%of agricultural water saving and 189 million cubic meters of waste water resources can make the system entropy reduced from 0.34 to 0.15 in 2030.And that can achieve the orderly development of water resources system.The research results have important significance to solve the contradiction between supply and demand of water resources in irrigation districts and to improve the efficient utilization of water resources.

Manasi River Basin;multi-dimension critical adjustment;system entropy;orderly development;high efficient utilization of water resources

X53；X821

A

10.13880/j.cnki.65-1174/n.2017.02.019

1007-7383(2017)02-0241-06

2016-03-25

国家自然科学基金(U1203282、41601579、41361096)，中国科学院野外站联盟（KFJ-SW-YW027-01），兵团科技创新团队((2014CC001)，石河子大学杰出青年（2012ZRKXJQ08）项目

杨明杰（1991-），男，硕士研究生，专业方向为水资源高效利用及生态水文学。

*通信作者：杨广（1983-），男，副教授，从事水资源高效利用及生态水文学的研究，e-mail:mikeyork@163.com。