基于Wi-Fi信号的LDCC-PDF分级时延估计

李 珂 任修坤 宗宇雷 李海文,2

1(解放军信息工程大学导航与空天目标工程学院 河南 郑州 450001)2(重庆通信学院 重庆 400035)

基于Wi-Fi信号的LDCC-PDF分级时延估计

李 珂1任修坤1宗宇雷1李海文1,2

1(解放军信息工程大学导航与空天目标工程学院 河南 郑州 450001)2(重庆通信学院 重庆 400035)

在室内无线定位领域，Wi-Fi技术因其低成本和广泛普及性更具研究价值和应用前景，而基于时延参数估计的定位算法则能满足高精度定位需求。针对现有各类时延估计算法在室内真实多径环境下估计精度差、复杂度较高的问题，提出一种基于前沿检测互相关和子载波相位差拟合LDCC-PDF(Leading-edge Detection based Cross-Correlation and Phase Difference Fit)的分级时延估计算法。首先对收发信号进行互相关，通过分步检测得到整数倍基带采样周期粗时延估计值，再对频域各收发数据子载波的相位差进行线性拟合，得出小数倍采样精时延估计值。以802.11n标准的长训练序列作为定位信号对算法进行了性能仿真。实验结果表明，该算法估计精度高，抗噪声性能良好，单径条件下均方根时延定位误差小于0.3米，多径非视距传输环境下误差小于1米。

Wi-Fi 时延估计 互相关 子载波相位差 线性拟合

0 引 言

现代社会的飞速发展和城市化节奏的不断加快，使人们对于位置服务的需求越来越大，基于卫星信号的全球定位系统(如GPS)以及移动数据网络提供了较为精确的室外定位导航服务(定位精度一般可达6～10米)[1]。但人们在日常出入的一些室内环境，如写字楼、商场超市、地下停车场等，往往因其处于卫星信号的覆盖盲区且移动数据网络信号也比较微弱而无法实时获取精确位置信息，因此寻找有效的高精度室内定位方法和技术具有重要意义。

相较于采用UWB[2]、红外线[3]、RFID[4]、蓝牙[5]等信号的现有定位技术，基于IEEE 802.11标准的无线局域网(Wi-Fi)因其低成本和广泛普及性在高精度室内定位方面更具有研究价值和应用前景。早期基于Wi-Fi室内定位方法的研究大多针对Wi-Fi信号强度(RSSI)展开，通过无线信号传播损耗模型建立信号强度与传播距离之间的映射关系[6-7]，但该类方法受室内实时环境变化因素影响较大，定位效果较差。为了克服这类问题，基于RSSI的位置指纹法被相继提出[8-9]，且不断改进更新，相关文献表示目前指纹法的定位精度可达1.6～5 m[10]。然而，要得到精度较高的指纹法需要以大量繁重的数据采集、预处理和后期维护工作为代价，且实际中室内人员或物体移动的随机性也将导致指纹地图性能下降甚至失效。为此，采用基于到达时间TOA(Time Of Arrival)测距技术的Wi-Fi定位方案更具鲁棒性，但由于无线信号的高速传播，该类方法对TOA估计精度要求非常高，1 m以内的定位精度需大约3 ns的时延估计精度。

传统的基带信号时延估计算法主要采用互相关，将接收信号与本地信号进行互相关运算，提取相关峰值得到估计值，算法简单易实现但受限于系统采样率与带宽，估计精度达不到要求[11-12]。802.11n标准的采样周期为0.05 μs，一个采样点偏移将导致15米的误差。相位检测法利用连续波发射到接收的相位差与时延成正比的特性来估计时延，精度优于相关法，但易受相位噪声影响，且当传输时延较大时存在相位模糊[13-14]，因此测距范围很小。为提高时延估计精度，Makki等人[15]首次提出了一种将互相关与相位差方法结合，运用于802.11g收发信号的高精度时延估计算法，该算法在理想视距单径传输环境下，基于WARP信号收发平台的实际测量定位误差为49 cm。

为克服基带信号采样周期的估计精度限制，部分学者提出采用过采样的方案[16-17]，跳过现有无线局限网硬件设置，通过使用采样率高达1 GS/s的A/D芯片和信号预处理算法，达到高分辨率(亚米级)的时延估计精度。这类方法的局限在于需要使用额外硬件配置，增加功耗和成本。

在室内多径非视距环境下，上述算法的估计性能都将明显下降，甚至失效。为克服多径效应影响，学者们提出了一些频域超分辨算法来提高时延估计精度，如MUSIC、ESPRIT及其改进算法等[18-21]，这些算法需要预先估计多径数目，再进行矩阵特征值分解，利用谱峰搜索得到TOA估计值[22]。目前这类算法在实际测量中可以提供3～5米的定位精度[23]，但往往需要以很高的信噪比和计算复杂度作为代价，硬件实现成本较高。

针对以上问题，本文从实时定位应用角度出发，在无需改变系统硬件配置的条件下，对基于Wi-Fi信号的时延估计算法进行研究。采用IEEE 802.11n标准基带信号，利用其前导训练序列，以系统采样周期为基础，将时延估计分为整数倍采样粗估计和小数倍采样精估计，以系统整数倍和小数倍采样周期时延为区分，提出一种基于前沿检测互相关和相位差拟合LDCC-PDF的分级时延估计算法。该算法仅使用基带信号，将互相关抗噪声性能良好、时延估计范围较大和子载波相位差算法估计精度高的特点相结合，与传统互相关和超分辨等时延估计算法相比，在多径环境下具有高精度低复杂度，实时性良好的优势。

1 信号模型

在无线通信中，多径环境下的时域信道模型可表示为：

(1)

τ0为首径传播时延，即所估计的信号传播TOA。在LOS传播环境中，τ0表示为信号传播最短直射路径所需时延；NLOS环境中，τ0为第一个含有信号成分的信号径的到达时间，可能是穿透障碍物的直射径，也可能是经反射和散射后的信号径。

采用OFDM调制的Wi-Fi信号，在室内环境中已广泛普及，本文采用目前应用较广的802.11n物理层基带信号作定位信号，利用传统前导码中的长训练序列进行时延估计。

802.11n标准支持多天线技术，第iTx个天线上发送的长训练序列的时域信号可表示为：

(2)

其中，Lk是长训练符号53个数据子载波上的频域序列(包含52个非零数据子载波和一个直流载波)，且：

L-26,26= {1，1,-1,-1,1,1,-1,1,-1,1,1,1,1,1,

1,-1,-1,1,1,-1,1,-1,1,1,1,1,0,1,

-1,-1,1,1,-1,1,-1,1,-1,-1,-1,

-1,-1,1,1,-1,-1,1,-1,1,-1,1,1,1,1}

(3)

为便于分析，选用单天线收发信号，则发送信号可表示为：

(4)

由式(2)无线信道冲激响应可得，发送信号经过多径信道后的接收信号可表示为：

y(t)=s(t)×h(t)=

exp(j2πkΔFt)

(5)

比较式(4)和式(5)，可将式(5)进一步表示为：

(6)

其中：

(7)

表示第k个子载波上的接收数据，Nk～N(0,σ2)是复高斯白噪声。

2 LDCC-PDF 分级时延估计算法

LDCC-PDF分级时延估计算法根据系统整数倍和小数倍采样周期分为粗时延和精时延两级时延估计，首先通过对传统互相关算法加以改进，提出适应多径环境的分步检测粗时延估计，得到粗时延值后利用不同数据子载波收发相移差存在线性关系来精确估计采样小数倍的时延。

2.1 分步检测粗时延估计

在理想单径信道下，通过寻找最大相关峰值可以得到较为精确的结果，但实际室内环境复杂多变，LOS径分量较少，甚至不存在，信号经过多径信道传播后将出现功率衰减和相位偏移等情况，接收信号为信号经过多径传播后的叠加，互相关结果表现为多径相关峰的叠加，会出现多个峰值，发生偏移。且在NLOS传播情况下，首达径往往不是功率最强的分量，微弱的首达径信号和强大的非直射径信号给TOA估计带来很大误差，此时传统峰值搜索方法将失效。现对传统互相关算法加以改进，采用分步检测的方法准确估计多径环境下的系统整数倍采样周期时延。

Step1 最大峰值检测

首先进行互相关检测，射频接收信号经下变频后变为基带信号，经采样率为fs的系统采样后，接收基带信号序列为y(n)，将其与本地序列进行互相关处理：

(8)

其中L为相关长度，记pm为最大峰值，d1为相关值最大时对应的采样点数，即：

(9)

Step2 首达峰检测

多径环境下TOA估计的目标在于寻找信号的首达径，检测出第一个含有信号的相关峰。多数情况下首径相关峰一般为最大峰之前与之相邻的某个峰，再往前出现的小峰值可能是由环境噪声产生，不可取。通过选取最优判决门限ξopt，确定首达峰搜索区域D={p|p>ξopt·pm}，该区域内出现的第一个峰即为首达径所在的峰(时延最小峰)，峰值为pξ，对应时延采样点为d2。

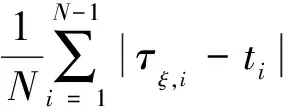
Step3 首达峰前沿检测

由于多径信号比LOS信号在传播时间上有一个附加的时延，首达径相关峰的前沿受多径叠加和干扰影响更小，因而其TOA估计可信度更高。在估计首达径所在峰上设置一新的阈值η，则该阈值所对应的较小时延即为该峰前沿上的TOA粗估计值，记录该时延采样点为d3。

根据上述原则判断各步时延采样点位置是否满足实际估计需求(d3≤d2≤d1)，最终粗时延估计值为：

(10)

2.2 子载波相位差拟合精时延估计

互相关时延估计的精度与系统带宽有关，只能获取到整数倍采样周期的时延，为满足定位需求，必须对一个采样周期内的时延进行精确估计。

根据频域接收数据表达式(7)，不考虑相位噪声，由相位变化的周期性可知由单个采样周期内引起的第i条径上的第k个和第k+δ个子载波的接收数据相对于发送数据的相移可分别表示为：

φk=θi-2πkΔFτi,fine

(11)

φk +δ=θi-2π(k+δ)ΔFτi,fine

(12)

其中τi,fine为第i条径上的小数倍时延，则相隔δ个子载波间的相移差为：

(13)

进而可得第i条径上由子载波相位偏移差导致的小数倍采样间隔时延为：

(14)

由式(13)可看出，时延一定时，不同收发子载波间的相位偏移差与子载波频率差成线性关系，因此可通过对不同子载波收发子载波间信号相位差进行线性拟合，当δ=1时，拟合斜率即为相邻子载波间的相移差，则小数倍采样间隔时延为：

(15)

式中，m为相位差随子载波频率变化的线性拟合梯度。

综上分析，单个采样间隔内的精确时延估计过程如下：

Step1 利用前期时域TOA粗估计值对原始接收数据进行采样点同步校正，再进行FFT，得到接收频域数据：

(16)

Step2 计算第k个子载波上的收发信号的相位差：

φk=∠Yk-∠Sk

(17)

Step3 计算相位差随不同子载波变化的最小均方误差线性拟合，按式(15)计算得到单个采样间隔内的时延τi,f。

结合粗时延估计，可知所求小数倍采样间隔时延为i=0时的值(定义τfine=τ0,fine)，则最终的TOA估计值为：

τ=τcoarse+τfine

(18)

3 算法仿真与结果分析

本节采用仿真实验来验证所提算法的性能，为了满足实际Wi-Fi相关产品最低参数需求，各仿真均采用IEEE 802.11n物理层协议规定的必选功能参数设置[25]，具体仿真条件如表1所示。

表1 仿真条件设置

(1) 粗时延估计性能仿真

单径信道下，对每个长训练符号进行粗时延估计，接收信号和发送信号进行互相关，对最大峰值检测算法进行Monte Carlo仿真，时延整数倍采样点随信噪比变化的正确检测概率如图1所示。可见当环境信噪比较高时，最大峰值检测粗时延估计效率很高，20 dB以上正确检测概率趋于稳定可达100%。

图1 单径信道下互相关最大峰值检测

多径信道下，对收发信号进行互相关，部分结果输出如图2所示。图2中可清楚地看到真实整数倍时延(采样点为10)对应的并非最大相关峰值(采样点为12)，而是出现在最大峰的前一个峰上，最大峰值检测性能将严重下降。分步检测时延估计算法中预先对首达峰检测的最优阈值进行估计，结果如图3所示。因此选择首达峰最优检测阈值为0.4，且在其他条件一定的情况下，不同多径信道环境下测试所得最优检测门限均分布于0.4～0.5倍最大峰值之间，证明该最优门限值在相似的信号传播环境中具有较好的普适性。首达峰前沿检测阈值η根据经验设为0.8pξ，按照分步检测粗时延估计方法进行Monte Carlo仿真，则互相关峰值检测、首达峰检测和首达峰前沿检测的整数倍粗时延估计正确检测概率如图4所示。可见在室内多径信号传播环境下，最大峰值检测严重恶化，正确率仅为0.2～0.3，经过首达峰检测和前沿检测处理后，正确概率大幅提升，可达到85%以上。注意到当信噪比小于0时，噪声分量为主要成分，算法性能受到严重影响，但当信噪比大于0后，算法性能趋于均衡，说明当信号分量大于噪声分量时，算法抗噪声性能较好。

图2 互相关输出示意图

图3 最优检测门限测试

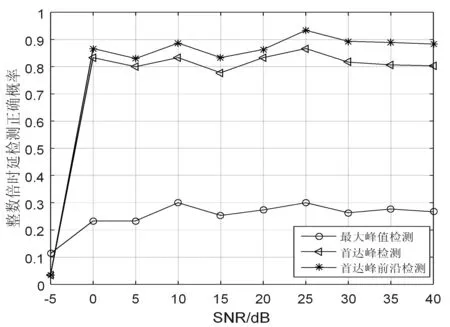
图4 多径环境下三种方案的正确检测概率

(2) 子载波相位差拟合精时延估计性能仿真

由粗估计结果对时域接收信号进行采样点对齐后通过FFT变换到频域，得到收发信号各数据子载波上的相位差(图5上)。相位偏移量随子载波序号呈线性变化，其中部分子载波相位偏移发生了2π的模糊，这是由接收信号部分子载波解调时发生相位旋转造成的。将其判断为相位差模糊噪声，对其进行去模糊处理，对调整后的相位差进行最小均方误差线性拟合(图5下)，则小数倍精确时延可由线性拟合斜率得到。分别在单径和多径环境下测试算法性能，如图6所示。单径估计性能明显优于多径，且受信噪比影响较小；多径条件下，高信噪比(>20 dB)时误差低于0.1 ns，信噪比较低(<20 dB)时的误差依然可以达到ns级，满足高精度室内定位需求。

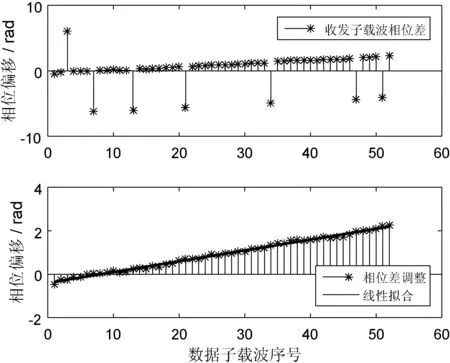
图5 收发子载波相位差

图6 精时延估计误差

(3) LDCC-PDF分级时延估计算法性能仿真

为验证所提算法的实际应用性能，将其与抗多径时延估计超分辨算法的经典算法MUSIC和文献[15]的方法作对比，分别在单径和多径条件下测试其算法性能，仿真参数如表1所示，实验结果如图7和图8所示。

分析结果可知，单径环境下，三者时延均方误差均可达到ns级，信噪比较低时本文和文献[15]算法接近，比MUSIC性能更好，定位误差基本可控制到1 m以内；当信噪比较高时，三者性能趋向稳定，MUSIC算法更优，但本文算法精度也可满足室内定位需求，均方根时延误差小于1 ns，即定位误差小于0.3 m。

图7 单径环境下时延估计算法对比

图8 多径环境下时延估计算法对比

多径环境下，图中可明显看出信噪比较低时，由于估计先验信息受噪声影响较大，MUSIC算法已经基本失效，文献[15]算法也因粗估计失效导致最终估计精度达不到定位需求。本文算法虽然性能比单径有所下降，但依然能够保持比较稳定的估计精度，高信噪比时达到3 ns的均方误差，即定位精度可达到1 m以下。

从计算复杂度上分析，MUSIC算法的复杂度较高，主要包括协方差矩阵估计、特征值分解和谱峰搜索三个部分，其中谱峰搜索计算量取决于时延搜索网格数，搜索网格越多，估计精度越高，但计算复杂度也会相应增加；文献[15]算法计算复杂度主要集中在一次求信号互相关和两次FFT计算上，运算量远远小于超分辨算法；与文献[15]相比，本文算法在粗估计过程中多了两次相关值搜索，但由于阈值搜索范围较小，运算量并未增加太多。

此外，与超分辨算法相比，本文涉及到的算法如互相关、FFT计算和求相位等，软硬件实现都比较容易，成本较低，适宜实际环境应用推广。

4 结 语

本文针对室内多径复杂环境下，现有Wi-Fi时延估计算法精度低、复杂度高的问题，提出了一种基于前沿检测互相关和频域数据子载波相位差线性拟合的分级时延估计算法(LDCC-PDF)。仿真结果表明，在理想单径传播环境下LDFF-PDF算法性能可以接近超分辨算法，同时也可以有效适应多径环境，在低信噪比条件下可获得更优的时延估计性能，多径瑞利衰落信道下可达到亚米级定位精度。此外，该算法复杂度较低，选用802.11n单个长训练序列作为定位信号，运算速度快，实时性高，可通过连续发送多个定位信号提高定位准确性。算法无需更改现有无线局域网硬件配置，实现成本较低，具备较高的实用价值，对实现高精度室内定位产品和服务具有实际意义。

另外，从性能上分析，本算法还有一些值得改进的地方，如采用时域数据处理和频域信道补偿等方法，增强低信噪比下的算法性能；利用802.11n的多天线技术对算法进行改进和增强处理，这些将被作为下一步的研究内容。此外，后续也会采用真实数据对本算法及其改进方案进行现实环境测试，以进一步评估算法实际应用性能。

[1] Farid Z,Nordin R,Ismail M.Recent Advances in Wireless Indoor Localization Techniques and System[J].Journal of Computer Networks & Communications,2013,2013(42):15-15.

[2] 张令文,杨刚.超宽带室内定位关键技术[J].数据采集与处理,2013,28(6):706-713.

[3] 吴琳.室内定位技术探讨[J].江西测绘,2013,2(2):34-37.

[4] 刘鹏,卢谭城,高翔.基于射频识别的室内定位技术综述[J].太赫兹科学与电子信息学报,2014(2):345-348.

[5] 卞和善.基于蓝牙4.0低功耗室内定位研究[D].北京:北京邮电大学,2015.

[6] Ahn H S,Yu W.Environmental-Adaptive RSSI-Based Indoor Localization[J].IEEE Transactions on Automation Science & Engineering,2009,6(4):626-633.

[7] Pivato P,Palopoli L,Petri D.Accuracy of RSS-Based Centroid Localization Algorithms in an Indoor Environment[J].IEEE Transactions on Instrumentation & Measurement,2011,60(10):3451-3460.

[8] Su J,Jin Y X.In doors location technology research based on WLAN[C]//Wseas International Conference on Instrumentation,Measurement,Circuits and Systems.World Scientific and Engineering Academy and Society (WSEAS),2007:109-114.

[9] 陈丽娜.WLAN位置指纹室内定位关键技术研究[D].上海:华东师范大学,2014.

[10] Lymberopoulos D,Liu J,Yang X,et al.A realistic evaluation and comparison of indoor location technologies:experiences and lessons learned[C]//The 14th International Conference on Information Processing and Sensor Network,2015:178-189.

[11] 倪浩.OFDM无线系统中的TOA估计技术研究[D].西安:西安电子科技大学,2010.

[12] 张丽艳,曾洁,李桂林.广义互相关时延估计法在汽车去噪系统中的应用[J].控制与系统学报,2006,27(3):52-55.

[13] 孙垂强.OFDM测距技术研究[D].西安:西安电子科技大学,2009.

[14] 易眠.时延及相关参数估计技术研究[D].成都:电子科技大学,2004.

[15] Makki A,Siddig A,Saad M M,et al.High-resolution time of arrival estimation for OFDM-based transceivers[J].Electronics Letters,2015,51(3):294-296.

[16] Nur K,Feng S,Ling C,et al.Application of the Improved FOCUSS for Arrival Time Estimation (IFATE) algorithm to WLAN high accuracy positioning services[C]//International Conference on Ubiquitous Positioning and Indoor Navigation Location Based Service,Oct.2012:1-8.

[17] Nur K,Feng S,Ling C,et al.A new time estimation technique for high accuracy indoor WLAN positioning[C]//International Conference on Navigation,2011:1-14.

[18] Schmidt R.Multiple emitter location and signal parameter estimation[J].IEEE Transactions on Antennas & Propagation,1986,34(3):276-280.

[19] Roy R,Kailath T.ESPRIT-estimation of signal parameters via rotational invariance techniques[J].IEEE Transactions on Acoustics Speech & Signal Processing,1990,37(7):984-995.

[20] Li X,Pahlavan K.Super-resolution TOA estimation with diversity for indoor geolocation[J].IEEE Transactions on Wireless Communications,2004,3(1):224-234.

[21] 王方秋,张小飞,汪飞.IR-UWB系统中基于root-MUSIC算法的TOA和DOA联合估计[J].通信学报,2014,35(2):137-145.

[22] 崔维嘉,陆杰青,裴喜龙,等.OFDM-WLAN系统互相关超分辨TOA估计[J].通信技术,2015,48(6):642-647.

[23] Zhao F,Yao W,Logothetis C C,et al.Comparison of Super-Resolution Algorithms for TOA Estimation in Indoor IEEE 802.11 Wireless LANs[C]//International Conference on Wireless Communications,NETWORKING and Mobile Computing.2006:1-5.

[24] 陈大伟.室内多径环境伪卫星定位精度分析与优化[D].哈尔滨:哈尔滨工业大学,2015.

[25] 杨昉,何丽峰,潘长勇,等.OFDM原理与标准——通信技术的演进[M].北京:电子工业出版社,2013.

LDCC-PDF HIERARCHICAL TIME DELAY ESTIMATION BASED ON WI-FI SIGNAL

Li Ke1Ren Xiukun1Zong Yulei1Li Haiwen1,2

1(InstituteofNavigationandAerospaceTargetEngineering,thePLAInformationEngineeringUniversity,Zhengzhou450001,Henan,China)2(ChongqingInstituteofCommunication,Chongqing400035,China)

Wi-Fi technology has its research value and application prospect in indoor positioning field due to its low cost and wide popularity, and positioning algorithm based on time delay estimation (TDE) can meet the requirement of high-precision positioning. Aiming at the problems of poor accuracy and high complexity of the existing TDE algorithms in indoor real multipath environment, this paper presents a hierarchical time delay estimation algorithm based on leading-edge detection cross correlation and subcarrier phase difference fit (LDCC-PDF). First, we perform cross correlation to the transmitted and

signal, getting the coarse time delay estimation of integer baseband sampling by the stepwise detection. Then the phase difference of each subcarrier in the frequency domain is linearly fitted, and the time delay estimation is obtained. The performance of the algorithm is simulated by using the long training sequence of 802.11n as the positioning signal. The experimental results show that the proposed algorithm has high accuracy and good anti-noise performance. The root-mean-square delay positioning error is less than 0.3 m for single path and less than 1 m for multi-path NLOS transmission.

Wi-Fi TDE Cross-correlation Subcarrier phase difference Linear fit

2016-06-01。李珂，硕士生，主研领域：无线定位技术。任修坤，讲师。宗宇雷，硕士生。李海文，博士生。

TP39

A

10.3969/j.issn.1000-386x.2017.06.029