舱门对内埋武器分离特性影响分析

闫盼盼， 张群峰， 金明

(北京交通大学 土木建筑工程学院， 北京 100044)

舱门对内埋武器分离特性影响分析

闫盼盼， 张群峰， 金明

(北京交通大学 土木建筑工程学院， 北京 100044)

为了研究是否考虑舱门及舱门不同开启姿态对内埋武器分离特性的影响，利用基于Menter剪应力输运k-ω湍流模型的分离涡模拟方法，结合6自由度刚体动力学方程和重叠网格技术，对超声速来流条件下某一简化内埋弹舱- 舱门- 弹体模型的三维流场进行了非定常计算，得到了不同条件下的弹体下落轨迹。结果表明：超声速来流条件下，流场中存在激波相交、激波剪切层反射等复杂流动现象，考虑舱门影响会使流场波系结构发生变化，弹体下落轨迹随之改变；弹体抬头角由0.5°增加到6.5°，弹体右偏航角由0.3°增加到2.5°，下落后期弹体下落速度增速减缓；舱门不同开启姿态对弹体竖直方向位移及俯仰运动影响较小，但会对弹体偏航产生较大影响；尽可能使舱门远离弹体可以有效地降低舱门对弹体偏航的影响，减小偏航角度，提高武器分离品质。

流体力学； 内埋武器舱； 舱门； 武器发射； 重叠网格； 分离涡模拟

0 引言

将通常由外挂方式携带的弹体放入战机内部，称为内埋挂载。内埋挂载方式下，弹体在投放前始终处于舱体内部，不与外流相接触，可以有效降低战机的可探测性并大幅度降低飞行阻力，提高飞行性能，因此内埋挂载方式广泛应用于新一代战机[1]。内埋挂载方式在具备上述优点的同时，也带来新的问题，当舱门开启之后，在舱体唇口处形成剪切层，剪切层失稳后呈现强非定常特性，流场中包含着极其复杂的流动物理现象，如波系相交和反射、剪切层/激波干扰等。弹体投放后，受复杂流场的影响，弹体下落速度、下落姿态会产生很大变化，使武器分离品质恶化，降低武器命中率，甚至威胁载机安全，因此内埋武器的安全分离问题成为研究热点[2]。杨俊等[3]通过数值模拟方法研究了有无弹射措施对弹体下落轨迹的影响，结果表明弹射投放比重力投放弹体下落品质明显提升。朱收涛等[4]通过数值模拟方法研究马赫数对弹体分离品质的影响，结果表明随着来流马赫数的提升，弹体分离品质恶化，原本安全的武器分离过程向着威胁载机安全的方向发展。冯必鸣等[5-7]通过数值模拟的方法对初始安装角、弹射速度、弹射角速度等对弹体下落的影响因素进行了数值模拟分析，研究表明这些因素均对弹体的下落姿态存在明显影响。吴继飞等[8-9]通过风洞试验方法探究了内埋武器投放的改进措施，发现采用前缘射流进行主动控制能有效降低武器分离过程中弹体受力波动，从而提高武器分离安全性。唐上钦等[10]研究了气动干扰对弹体下落的影响，结果表明气动干扰对内埋导弹发射后初始弹道和自控终点纵向、侧向散布影响明显。现有研究多采用雷诺平均(RANS)方法来进行数值模拟计算。然而针对内埋武器舱内的强非定常、强涡流场，RANS方法会引入过多的耗散，无法准确捕捉精细流动结构。导致计算结果与实际情况存在较大偏差，因此需要选用更高精度的数值方法进行计算。同时为了研究问题的简便，大多数研究将内埋弹舱抽象为简单的矩形腔体，并且不考虑舱门的存在。即使研究中考虑了舱门但也并未将舱门作为一个重要影响因素进行详细的分析。

在超声速来流条件下，舱门的存在会使舱门附近流场产生复杂的波系结构，激波作用在弹体表面会使得弹体表面压力发生显著改变。此外舱门引发的波系还会与腔体前缘波系、弹体头部波系产生波系相交及反射，使弹体下落流场变得更为复杂，导致弹体所受气动力及力矩发生改变，从而改变弹体下落轨迹及弹体姿态。同时舱门的不同开启姿态会在流场中产生不同的波系结构，也会导致弹体下落轨迹发生变化。因此有必要将舱门及舱门开启姿态作为弹体安全分离的重要因素进行深入研究。本文应用成熟商业软件Starccm+，采用基于Menter剪应力输运(SST)湍流模式的改进延迟分离涡模拟(IDDES)方法，结合6自由度刚体动力学方程和重叠网格技术，研究超声速来流条件下，舱门有无及舱门的不同开启姿态对弹体分离品质的影响，以期为武器安全分离提供一定的理论参考。

1 数值计算方法

1.1 控制方程

本文主要研究弹体投放运动，考虑黏性影响适用于动网格的三维、可压缩、非定常、守恒型控制方程[11-13]表示如下：

(1)

式中：W为守恒变量；Fc为对流矢通量；Fv为黏性矢通量；Q为源项；Ω为控制体；dS为面元；vt为控制体表面的逆变速度，

(2)

g为微元面积dS的运动速度矢量，n为面元dS的外法向矢量，nx,ny,nz为其3个方向上的分量。

1.2IDDES方法

Spalart提出的DES97中RANS模型选用的是S-A模型，在之后Strelets又做了进一步的扩展[14]，提出以SST模型代替S-A模型的SST-IDDES模型，使得新的混合模型兼有了SST模型的诸多优点。与S-A模型不同，SST-IDDES以隐式的方法引入长度尺度：

(3)

lRANS为RANS模型长度尺度，表达式为

lRANS=k1/2/Cμω,

(4)

lIDDES为亚格子长度尺度，表达式为

lIDDES=min{max [cwdw,cwhmax,hwn],hmax},

(5)

式中：hwn是垂直壁面方向的网格步长；dw为到壁面距离；cw为经验常数，取0.15；hmax为hwn的最大值；f1为经验混合函数；CDES为比例系数；k为湍动能；ω为湍流耗散比；Cμ为常数0.09.

将以上长度尺度引入到SSTk-ω模型k方程的耗散项中得到IDDES公式为

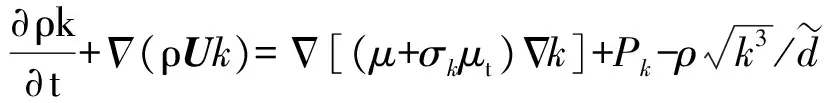
(6)

(7)

式中：ρ为密度；t为时间；U为速度向量；μ为分子黏性系数；μt为湍流黏性系数；Pk为湍动能生成项；η=0.075；ψ=ψ1f1+ψ2(1-f1)，ψ1=5/9，ψ2=0.44；σk=0.85；σω=0.85；σω2=0.856.

相比于最初版本DES97[15]及DDES[16]方法，IDDES加入了壁面模化的大涡模拟分支(WMLES)，在保留了DES类方法优点的同时，成功克服了对数律不匹配、网格诱导分离、模型应力损耗等问题[17]。

1.3 6自由度刚体动力学方程

本文选择与战机相连的武器舱为惯性坐标系来描述弹体从武器舱分离后的运动过程。导弹运动方程组是描述作用在导弹上的力、力矩与导弹参数之间关系的一组方程，称之为6自由度运动方程组。它由描述质心运动和导弹姿态变化的动力学方程、运动学方程、角度几何关系等3类方程所组成。具体公式为

(8)

式中：Fx、Fy、Fz为战机坐标系下3个坐标方向上弹体所受的力(包括气动力和重力等)；vx、vy、vz为3个方向的速度；m为弹体质量。

(9)

式中：Mx、My、Mz为弹体所受外力矩在弹体坐标系下的3个分量；Ix、Iy、Iz为弹体绕自身3个主轴的转动惯量；θx、θy、θz为弹体绕自身3个主轴的转动角速度。

(10)

式中：α、β、γ为弹体在战机坐标系下3个方向的姿态角。

1.4 重叠网格法

重叠网格法中存在多套相互交叠的网格区域，分别称为背景网格区域和重叠网格区域。其基本原理是通过重叠部分的网格在不同的区域之间传递计算信息[18-19]。通常情况下背景网格区域是静止的，不做相对运动，而重叠网格区域一般用来模拟相对运动。

重叠网格法中网格被划分为3种类型：活动网格(active)、隐藏网格(inactive)、插值网格(acceptor)。插值网格作为区分活动网格和隐藏网格的边界，与重叠网格区域的边界相邻。插值网格的作用是将两套网格的解耦合起来。插值网格的值由另一套网格上经一定算法选中的贡献单元，通过插值提供。贡献单元与插值单元邻近但属于不同的网格区域。

1.5 数值方法验证

由美国空军发起的第1次分离投放试验采用机翼/挂架/带舵外挂物(WPFS)模型，捕获轨迹试验(CTS)测试由诺德工程发展中心(AEDC)完成，并得到了较为详细的CTS测量结果数据，被广泛地应用于数值方法的校准[20]。本文以该模型试验来验证采用本文所选用数值方法并应用重叠网格技术和刚体动力学方程模拟弹体投放过程的准确性。

WPFS模型几何外形如图1所示，机翼根部弦长为7.62 m，半翼展6.604 m，采用NACA64A010翼型，机翼面积为51.031 m2. 外挂物长3.387 m，直径0.508 m，弹体质量为907.5 kg，来流马赫数为0.95.

图1 WPFS模型几何外形Fig.1 Wing-pylon-store geometry

模型网格划分为两个区域，包含机翼及挂架的背景网格区域和包含弹体的重叠网格区域。背景网格区域网格总数为1 150万，重叠网格区域网格总数为320万，计算时间步取1×10-3s.

图2(a)为3个方向弹体质心位移随时间变化曲线。从图2(a)中可以看出，计算得到的弹体位移变化与试验符合较好，由于弹射力作用，弹体下落方向位移要远大于另外两个方向的位移。图2(b)为弹体滚转、偏航、俯仰姿态角随时间变化曲线，同样由于弹体弹射力作用，在下落初期，弹体俯仰角度增长最快，但撤去弹射力后，在重力和气动力共同作用下俯仰角又开始减小，其余两个方向姿态角保持持续增加的趋势。从图2可以看出，本文采取的数值方法可以准确地模拟弹体下落运动。

图2 弹体位移及姿态角随时间变化Fig.2 Displacement and angular orientation of missile vs. time

2 计算模型和网格划分

2.1 计算模型

本文所选用的计算模型为简化的弹舱- 舱门- 弹体模型，计算模型如图3所示，弹舱长、宽、高为4.2 m×2 m×0.7 m，采用全模进行计算，总的计算域范围选取为100 m×35 m×50 m. 舱门为两段式舱门，外侧表面光滑，第1段内侧有增加强度的凸起肋板。计算中考虑了舱门3种不同的开启姿态，分别对应图4中类型A～类型C. 类型A中舱门打开角度约为110°，第2段折起；类型B舱门开启角度同样为110°，但将第2段展开，与第1段共线；类型C与类型B舱门展开形式相同，但舱门开启角度减小为90°. 舱内存在3个弹体挂载位置，中间挂载弹体两侧受舱门影响较为对称，而两侧挂载位置的弹体受单侧舱门影响更大，针对于本文研究问题，只对两侧挂载弹体进行深入研究。弹体与舱门的相对位置如图4所示，图4中视角为从弹体尾部看向弹体头部，逆着来流方向，与图3相反。弹体详细参数见表1.

图3 简化计算模型Fig.3 Simplified simulation model

图4 舱门不同开启类型Fig.4 Opening modes of bay door

弹体长度/m32弹体直径/m018弹体质心位置/m距头部尖点184弹体质量/kg170弹体绕x轴的转动惯量Ix/(kg·m2)137绕y轴、z轴的转动惯量Iy、Iz/(kg·m2)120

2.2 网格尺寸选择

本文采用重叠网格法来实现弹体的运动，因此将计算网格划分为两个区域：包含了腔体及整个计算域的背景网格区域以及包含了弹体的重叠网格区域。根据预估的弹体下落轨迹范围对背景网格进行区域加密，保证弹体下落过程中不超出网格加密区范围。同时为了保证弹体下落过程中网格挖洞过程的鲁棒性并且保证网格交界处插值有足够的精度，在网格划分时使重叠网格区域与背景网格区域交界处网格比例在1～1.2之间。网格类型选取为非结构化Trim网格，垂直壁面方向第1层网格尺寸设置为2×10-6m以使得y+接近于1. 背景网格数量为2 150万，重叠区域网格数目为400万。网格密度分布如图5所示。

图5 弹体中心截面网格分布(B-B截面)Fig.5 Grid distributionof central plane of missile (B-B section)

2.3 计算条件

分别计算了超声速来流条件下(马赫数为1.50)是否考虑舱门及舱门的不同开启姿态对弹体分离品质的影响。详细工况见表2. 在建立起流场之后，又对舱体带弹状态进行了0.1 s的非定常计算，之后弹体开始下落，下落时长为0.3 s，总计算时间为0.4 s. 计算时间步长选取为5×10-4s，非定常计算采用双重时间步法，内迭代步设置为20步，可以保证残差下降两个量级。

表2 计算工况Tab.2 Simulation cases

3 结果分析

由图3可知，本文算例中坐标系选取以x轴为逆航向，y轴向上，z轴向左，则按此坐标系定义，弹体低头为正、左偏航为正。

3.1 舱门有无对弹体分离特性的影响

图6(a)～图6(c)为弹体竖直方向受力、速度及位移随时间变化曲线。图7(a)～图7(c)为弹体俯仰力矩、俯仰角速度及俯仰角随时间变化曲线。图8(a)～图8(c)为弹体偏航力矩、偏航角速度及偏航角随时间变化曲线。

图6 弹体竖直方向受力、速度、位移随时间变化Fig.6 Vertical force, velocity and displacement of missile vs. time

从图6(a)、图7(a)和图8(a)可以看出，由于内埋舱流场呈现强非定常特性，下落前期受其影响弹体受力及力矩存在明显的波动。从图6(b)、图6(c)中可以看出，工况1中不考虑舱门存在时，弹体下落速度近似保持线性增长，而工况2考虑舱门影响后，投放后期弹体下落速度增速减缓。然而由于下落时间较短，两种工况的下落位移曲线差别不明显，工况2弹体下落位移略小于工况1.

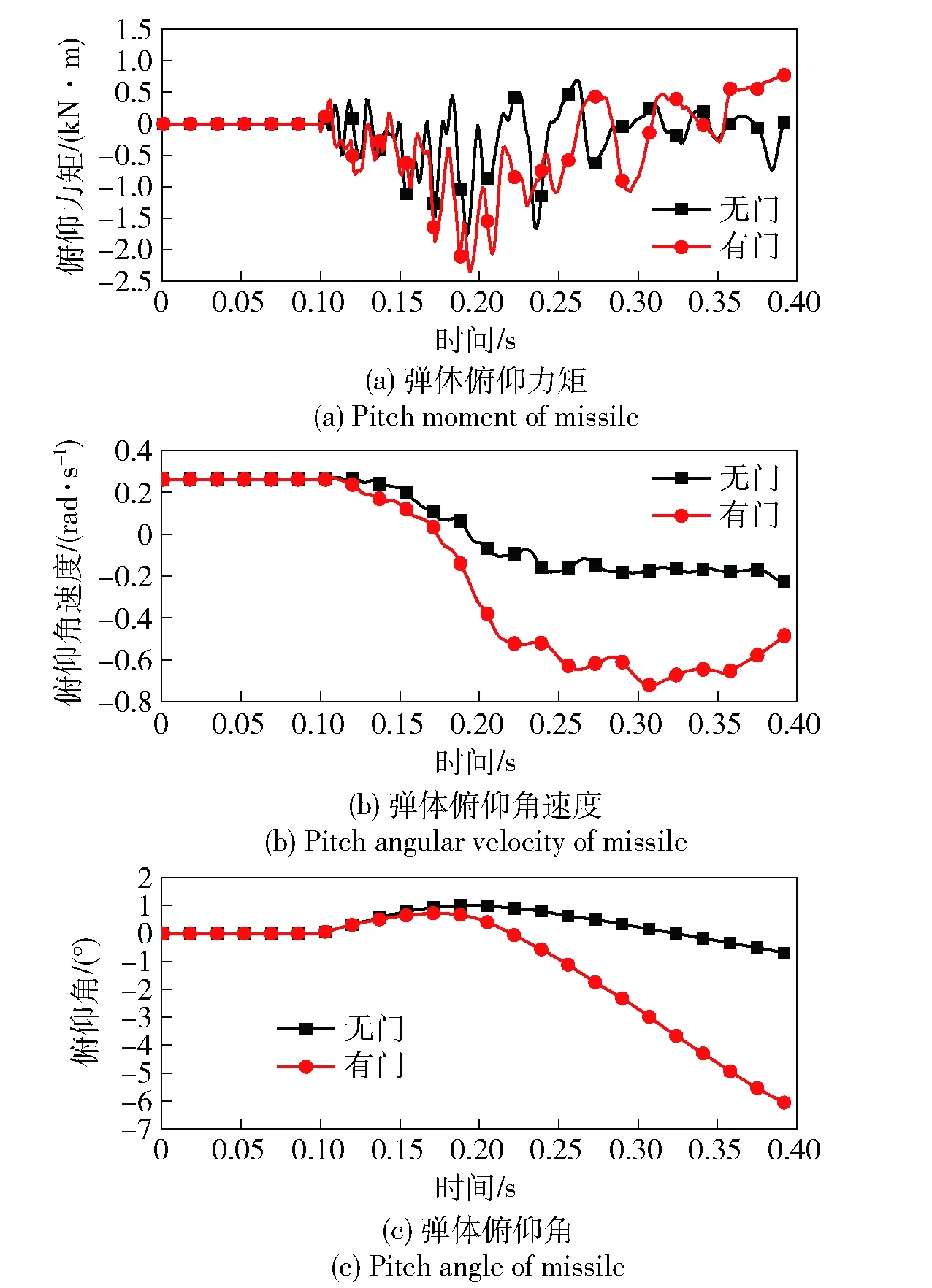
图7 弹体俯仰力矩、角速度、俯仰角随时间变化Fig.7 Pitch moment, pitch angular velocity and pitch angle of missile vs. time

图8 弹体偏航力矩、角速度、俯仰角随时间变化Fig.8 Yaw moment, pitch angular velocity and pitch angle of missile vs. time

3.1.1 弹体下落初期(t为0.10～0.18 s)

从图7(a)弹体俯仰力矩曲线可知, 在t为0.10～0.18 s时间段，弹体所受俯仰力矩保持为抬头力矩并持续增大。由图7(b)中可知，弹体初始俯仰角速度为低头角速度，大小为0.261 8 rad/s，受抬头力矩的影响，弹体下落后低头角速度不断降低，最终在t=0.18 s减小到0，之后转变为抬头角速度。此阶段由于俯仰角速度仍保持为低头角速度，因此弹体呈现低头姿态，最大低头角度为1°左右。从图8可知，弹体偏航角速度及偏航角均较小。该阶段为弹体穿越舱门唇口位置剪切层出舱过程，舱门对弹体下落影响还不明显，从图8中可以看出，是否考虑舱门存在，对于该时间段弹体下落轨迹及姿态角变化影响不大，两种工况下弹体下落参数均保持相近的变化趋势。

以工况1为例对流场进行详细分析，工况2与其类似，不再赘述。图9为工况1中t=0.15 s时通过弹体中心位置，流场z截面马赫数分布云图。图10为弹体上下表面对称线压力系数分布曲线。从图10中可以看出，此时弹体正穿越剪切层出舱。弹体头部受来流直接撞击，来流一部分动能转化为压能，使得弹体头部出现局部高压区。弹体上表面为舱体唇口附近低速气流，压力相对较高；弹体下部为高速来流，压力较低。弹体中后部上表面压力明显高于下表面，因此该阶段作用在弹体上的俯仰力矩保持为抬头力矩。

图9 无舱门时t=0.15 s流场z截面马赫数分布云图Fig.9 Mach number contours of z cross section for t=0.15 s

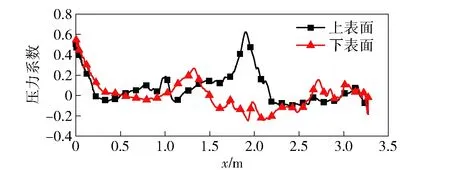
图10 弹体上下表面对称线压力系数分布曲线Fig.10 Pressure coefficient distribution of symmetric lines on upper and lower surfaces

3.1.2 弹体下落中期(t为0.18～0.31 s)

舱门的存在使流场中波系发生改变，从图7、图8可知，受其影响弹体出舱后在t为0.18～0.31 s这一时间段，两种工况中弹体所受俯仰力矩、偏航力矩变化趋势出现差别，弹体俯仰角及偏航角呈现出显著差异。由图7(a)、图7(b)可以看出，该阶段工况2中弹体所受俯仰力矩高于工况1，弹体抬头角速度迅速升高，在0.31 s时抬头角速度达到0.75 rad/s，弹体抬头角度为3.5°. 工况1中弹体抬头角速度仅为0.2 rad/s，弹体俯仰角约为0°. 由图8可知工况2中弹体受右偏航力矩，使得弹体右偏航角速度持续增加，在0.31 s达到0.3 rad/s，弹体头部远离舱门方向偏航角度不断增大，弹体下落0.4 s后，弹体右偏航角度达到2.5°，而工况1中弹体偏航角速度及偏航角始终保持在0附近。

图11为t=0.20 s流场y截面马赫数分布云图，截面位置为图4中所示A-A截面。从图11中可看出，工况1由于不考虑舱门，弹体周边流场波系相对简单，主要为弹体头部斜激波，记为激波类型Ⅰ，弹体左右两侧流场对称性较高。在弹体右侧尾部位置处还存在一道激波，这是由于受到舱体唇口处剪切层的影响所产生。

图11 t=0.20 s流场y截面马赫数分布云图(A-A截面)Fig.11 Mach number contours of y cross section for t=0.20 s (A-A section)

与工况1相比，工况2受舱门影响流场中波系结构发生了明显的改变，可以观察到3种主要类型激波：类型Ⅰ为弹体头部斜激波，类型Ⅱ为由于舱门存在所产生的斜激波，类型Ⅲ是由于舱门内侧肋板影响产生强分离流动所引发的斜激波。这3类激波在流场中形成了更加复杂的相交及反射波系。左右两侧舱门产生的类型Ⅱ激波发生异族激波相交并产生透射激波Ⅱ1，透射激波Ⅱ1进一步与激波Ⅲ发生相交，产生透射激波Ⅱ2及透射激波Ⅲ1. 透射激波Ⅲ1继续与类型Ⅰ激波相交，生成透射激波Ⅰ1及透射激波Ⅲ2，透射激波Ⅲ2打在弹体表面。同时在弹体左侧类型Ⅰ与类型Ⅲ两道激波也发生了激波相交。由于弹体位置偏向左侧舱门，因此弹体两侧波系结构并不完全对称。

图12为t=0.20 s通过弹体中心位置，流场z截面马赫数分布云图，截面位置为图4中所示B-B截面。工况1竖直截面流场中可观察到两种类型激波：除了上文提到的类型Ⅰ弹体头部斜激波外，还存在类型IV腔体前缘斜激波。弹体头部斜激波与舱体唇口位置处剪切层相互作用，反射为膨胀波Ⅰ1.

图12 t=0.20 s流场z截面马赫数分布云图Fig.12 Mach number contours of z cross section for t=0.20 s

工况2竖直截面流场中可观察到4种主要类型激波：类型Ⅰ弹体头部斜激波，类型Ⅱ舱门引起的激波以及类型IV腔体前缘斜激波。类型Ⅱ激波由舱门位置横向朝腔体内部延伸，在腔体前缘位置与类型IV激波相交，由于类型IV斜激波强度较弱，因此相交后透射激波不明显。波后气流持续膨胀加速，随后在弹体与剪切层之间产生一道新的斜激波，为流场中第V类激波。类型Ⅰ与类型V激波发生异族激波相交，产生透射激波V1和透射激波Ⅰ1，透射V1作用在弹体头部上表面，透射激波Ⅰ1与剪切层相互作用，反射为膨胀激波Ⅰ2. 受流场复杂波系的影响，弹体表面压力分布不均匀，呈现高低压交替分布，同时引起弹体尾部与剪切层之间的区域压力升高。

图13为流场y截面即A-A截面流场压力系数分布云图。从图13中可以看出，与工况1相比，受舱门影响的工况2中弹体所处流场压力分布不均匀性增强。由于波系的作用及舱门内侧分离流动的影响，弹体尾部流场压力明显高于前方，同时由于弹体左右两侧波系结构不对称，左右两侧压力分布也呈现较强的不对称性。弹体表面压力分布的不均匀使得工况2中弹体受到较大的俯仰及偏航力矩。

图13 t=0.20 s流场y截面压力系数分布云图Fig.13 Pressure coefficient contours of y cross section for t=0.20 s

图14 弹体压力系数分布云图及表面对称线压力系数曲线Fig.14 Pressure distribution of missile and pressure coefficient distribution of symmetric lines on upper and lower surfaces

图14为弹体x截面压力系数分布云图及弹体表面不同周向位置压力系数分布曲线。从图14中可知，弹体表面压力呈现高低压交替的不均匀分布，且考虑舱门的工况弹体表面压力波动更剧烈。从弹体上下表面对称线压力系数分布曲线中可知，工况2弹体后部上下表面压力差较大，作用在弹体上使弹体产生较大的抬头力矩。这是由于舱门引发的类型Ⅱ激波使得纵向平面上波系变得更加复杂，从而导致弹体后部上表面压力升高，压差增大。因此考虑舱门时，弹体受到的抬头力矩要大于不考虑舱门的工况。较大的抬头力矩使得弹体产生更大的抬头角速度及抬头角。从弹体左右两侧表面对称线压力系数分布曲线可以看出，不考虑舱门时弹体左右两侧压力分布对称性较强，曲线基本重合。因此弹体受到偏航力矩很小，在下落过程中偏航角速度及偏航角维持在0附近。而考虑舱门后，由于不对称波系结构的影响，弹体左右两侧压力分布差别较大，受激波影响，弹体头部靠近舱门一侧出现局部高压区，使得弹体产生右偏航力矩，下落过程中弹体右偏航角度持续增加。

3.1.3 弹体下落后期(t为0.31～0.40 s)

在t为0.31～0.40 s这一阶段，两种工况弹体俯仰力矩及弹体俯仰角速度同样表现出不同的变化趋势，工况1此阶段弹体俯仰力矩趋于平稳，其幅值在0附近上下波动，弹体抬头角速度维持在0.2 rad/s小幅震荡。而工况2中，弹体受到的俯仰力矩开始急剧减小并转为低头力矩，抬头角速度逐步降低，在t=0.40 s时，抬头角速度由0.75 rad/s降低为0.50 rad/s. 在t=0.40 s时，工况1与工况2弹体最终抬头角度分别为0.5°和6.5°，二者相差达到6°.

图15 t=0.32 s流场z截面马赫数分布云图Fig.15 Mach number contours of z cross section for t=0.32 s

图15为t=0.32 s时流场马赫数分布云图。从图15中可以看出，工况1中弹体此时俯仰角度在0°左右，同时由于不考虑舱门影响且此时弹体远离剪切层，弹体上下两侧流场较为对称，仅在弹体上表面存在一道弱透射激波的作用，因此弹体受到的俯仰力矩很小。而工况2中舱门前缘强斜激波与弹体头部斜激波相交后产生的透射激波作用在弹体头部上表面，使弹体头部上表面压力升高，该高压区对弹体产生的俯仰力矩为低头力矩。同时，这一阶段弹体存在一定的迎角，弹体中后部下表面及弹翼下表面压力升高，对弹体产生的俯仰力矩同样为低头力矩，随着弹体下落迎角持续增加，产生的低头力矩逐渐增大。由于上述两种原因，弹体抬头力矩不断降低并最终转为低头力矩。

通过上述分析可以看出，舱门的存在会使弹体在下落后期的分离速度增速放缓，弹体偏航角及俯仰角大幅增加，不利于武器安全分离。因此在以后研究中应当考虑舱门的存在对弹体下落轨迹的影响。

3.2 舱门不同开启姿态对弹体分离特性影响

图16(a)～图16(f)分别为不同舱门开启姿态下弹体竖直方向受力、竖直方向位移、俯仰力矩、俯仰角、偏航力矩、偏航角随时间变化曲线。从图16(a)～图16(c)中可以看出，不同工况下弹体竖直方向受力、下落位移、俯仰力矩及俯仰角均保持相近的变化规律，受舱门开启姿态影响较小，这是因为舱门的不同开启对于流场纵向波系的影响较小。然而，从图16(e)、图16(f)可以看出，弹体偏航力矩及偏航角存在明显的差异。在弹体下落中期，类型B与另外两类开启方式相比，弹体所受偏航力矩存在较大的差别。受此影响，类型A开启姿态下弹体右偏航角为2.5°，类型B开启方式下右偏航角降低为0.75°，类型C开启方式下弹体右偏航角又增加到3°. 同时可以看出弹体偏航角度均为负值，弹体头部均远离左侧舱门向右偏转。

图16 弹体竖直方向受力、位移、俯仰力矩、俯仰角、偏航力矩、偏航角随时间变化Fig.16 Vertical force, displacement, pitch moment, pitch angle, yaw moment and yaw angle of missile vs. time

与图11类似，截取不同工况下流场y截面马赫数分布云图，如图17所示。图17中截面位置选取均穿过舱门第2折段，截面范围为弹体和左侧舱门即图4中蓝色框线标示区域。类型A舱门第2段向弹体方向折叠，靠近弹体位置，舱门波系对弹体表面压力分布影响更强。弹体与舱门之间的波系结构强度高，因此弹体头部靠近舱门的一侧压力较大，使得弹体产生右偏航力矩，弹体头部远离舱门偏转。类型B舱门开启角度与类型A相同均为110°，但舱门第2段展开，从图17中可以看出，与类型A相比，舱门第2段离弹体较远，舱门与弹体间波系强度降低，波系作用在弹体上的位置后移。这使得弹体头部靠近舱门一侧压力降低，高压区位置也向后移动，因此在弹体上产生的偏航力矩较小，最终弹体右偏航角度仅为0.75°. 类型C舱门开启方式与类型B类似，但是开启角度减小为90°，使舱门第2段距离弹体距离再次减小，因此弹体偏航角度再次升高。从上述分析可知，尽可能使舱门远离弹体可以有效减小舱门对弹体偏航的影响。

图17 不同工况流场y截面马赫数分布云图Fig.17 Mach number contours of y cross section in different cases

4 结论

1)超声速来流条件下，流场中存在复杂的波系结构，在弹体与剪切层之间发生激波相交、激波剪切层反射等复杂流动现象。考虑舱门影响后，在弹体与舱门之间也形成了复杂的相交反射波系结构，对弹体下落轨迹产生强烈影响。在下落3.5 m距离后，不考虑舱门时弹体俯仰角度为-0.5°，考虑舱门影响后弹体俯仰角增加到-6.5°，相差达6°，弹体偏航角从-0.3°增加到-2.5°，同时在下落后期弹体下落速度增速放缓，不利于武器安全分离。

2)舱门不同开启姿态对弹体竖直方向位移及俯仰运动影响较小，但会对弹体偏航运动产生较大影响。类型B开启姿态偏航角最小，仅为-0.75°，而类型A 与类型C偏航角度较大分别为-2.5°、-3°. 这表明尽可能使舱门远离弹体可以有效降低舱门对弹体偏航的影响，减小偏航角度，提高武器分离品质。

References)

[1] 郭亮, 王纯, 叶斌，等. 采用流动控制的超声速内埋物投放特性研究[J]. 航空学报, 2015, 36(6): 1752-1761. GUO Liang, WANG Chun, YE Bin, et al. Investigation on characteristics of store release from internal bay in supersonic flow

under flow control [J]. Acta Aeronauiica et Astronautica Sinica, 2015, 36(6): 1752-1761. (in Chinese)

[2] 汤济新. 机载武器发射技术及其研究[J]. 航空科学技术, 2016, 27(4): 1-8. TANG Ji-xin. Study on airborne weapon launch technology [J]. Aeronautical Science & Technology, 2016, 27(4): 1-8. (in Chinese)

[3] 杨俊, 李骞, 谢云恺，等. 超声速内埋武器分离数值研究[J]. 弹箭与制导学报, 2015, 35(4): 171-174. YANG Jun, LI Qian, XIE Yun-kai, et al. Numerical studies on store separation from a weapon bay at supersonic speed [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2015, 35(4): 171-174. (in Chinese)

[4] 朱收涛, 曹林平, 封普文，等. 平飞时内埋导弹弹射分离仿真与研究[J]. 电光与控制, 2012, 19(9): 67-71. ZHU Shou-tao, CAO Lin-ping, FENG Pu-wen, et al. Simulation of missile separation from internal weapon bay [J]. Electronics Optics & Control, 2012, 19(9): 67-71. (in Chinese)

[5] 冯必鸣, 聂万胜, 车学科.超声速条件下内埋式武器分离特性的数值分析[J].飞机设计, 2009, 29(4):1-5. FENG Bi-ming, NIE Wan-sheng, CHE Xue-ke. Simulation of the store separation from a cavity at supersonic speed [J].Aircraft Design, 2009, 29(4):1-5. (in Chinese)

[6] 冯必鸣,聂万胜,车学科. 初始投放条件对内埋式导弹分离轨迹的影响[J]. 飞行力学, 2009, 27(4): 62-65. FENG Bi-ming, NIE Wan-sheng, CHE Xue-ke. Effect of initial conditions on separation trajectory of the internal missile [J].Flight Dynamics, 2009, 27(4): 62-65. (in Chinese)

[7] 冯必鸣,聂万胜,车学科，等. 安装角度对内埋式导弹分离特性的影响[J]. 空气动力学学报, 2010, 28(6): 672-675. FENG Bi-ming, NIE Wan-sheng, CHE Xue-ke, et al. Effect of fixing angle to separation characteristics of internal store [J]. Acta Aerodynamica Sinica, 2010, 28(6): 672-675. (in Chinese)

[8] 吴继飞, 罗新福, 徐来武，等. 内埋武器分离特性及其改进方法研究[J]. 空气动力学学报, 2014, 32(6): 814- 819. WU Ji-fei, LUO Xin-fu, XU Lai-wu, et al. Investigation on internal weapon separation characteristics and flow control methods [J]. Acta Aerodynamica Sinica, 2014, 32(6): 814-819. (in Chinese)

[9] 吴继飞,罗新福,范召林. 内埋式弹舱流场特性及武器分离特性改进措施[J]. 航空学报, 2009, 30(10):1840-1845. WU Ji-fei, LUO Xin-fu, FAN Zhao-lin. Flow control method to improve cavity flow and store separation characteristics [J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(10):1840-1845. (in Chinese)

[10] 唐上钦, 黄长强, 翁兴伟. 考虑气动干扰的导弹内埋式发射弹道研究[J]. 弹箭与制导学报, 2013, 33(3): 138-142. TANG Shang-qin, HUANG Chang-qiang, WENG Xing-wei. The study on trajectory of missile separating from cavity with aerodynamic interference considered [J]. Journal of Projectiles，Rockets，Missiles and Guidance, 2013, 33(3): 138-142. (in Chinese)

[11] Blazek J. Computational fluid dynamics principles and applications [M].London：Elsevier, 2005: 16-18.

[12] Tamura Y, Fujii K. Conservation law for moving and transformed grids[C]∥AIAA 11th Computational Fluid Dynamics Conference. Orlando, FL, US: AIAA, 1993: 519-522.

[13] 刘伟. 细长机翼摇滚机理的非线性动力学分析及数值模拟方法研究[D]. 长沙: 国防科学技术大学, 2004. LIU Wei. Nonlinear dynamics analysis for mechanism of slender wing rock and study of numerical simulation method [D]. Changsha: National University of Defense Technology, 2004. (in Chinese)

[14] Strelets M. Detached eddy simulation of massively separated flows[C]∥39th Aerospace Sciences Meeting and Exhibit. Reno, NV, US: AIAA, 2001: 1-18.

[15] Spalart P R, Jou W H, Strelets M, et al. Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach[J]. Advances in DNS/LES, 1997, 15(1): 4-8.

[16] Spalart P R, Deck S, Shur M L, et al. A new version of detached eddy simulation, resistant to ambiguous grid densities [J]. Theoretical and Computational Fluid Dynamics, 2006, 20(3): 181-195.

[17] Shur M L, Spalart P R, Strelets M. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities [J].International Journal of Heat and Fluid Flow, 2008, 29(6): 1638-1649.

[18] 朱自强. 应用计算流体力学[M]. 北京：北京航空航天大学出版社, 1998: 173-174. ZHU Zi-qiang. The application of computational fluid dynamics [M]. Beijing:Beijing University of Aeronautics and Astronautics Press, 1998: 173-174. (in Chinese)

[19] 阎超. 计算流体力学方法及应用[M]. 北京：北京航空航天大学出版社, 2006: 197-217. YAN Chao. The computational fluid dynamics method and its application [M]. Beijing:Beijing University of Aeronautics and Astronautics Press, 2006: 197-217. (in Chinese)

[20] Heim E R. CFD wing/pylon/finned store mutual interference wind tunnel experiment[R]. TN, US: Arnold Engineering Development Center, 1991.

Effect of Bay Door on Separation Characteristics of Internal Store

YAN Pan-pan， ZHANG Qun-feng， JIN Ming

(School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China)

To study the effects of bay door and door opening states on the separation characteristics of internal store, a simplified buried weapon bay-door-missile model is simulated using SSTk-ωIDDES method, six degrees of freedom rigid body dynamics equations and overset mesh method under the condition of supersonic inflow. The separation trajectories of missile bodies in different cases were obtained. The results show that, in supersonic flow, shock intersection and shock shear layer reflection are present in the flow field. Considering that the bay door may make the wave structure changed, the trajectory of missile is also changed. The upward pitch angle of missile increases from 0.5° to 6.5°, the right yaw angle of missile increases from 0.3° to 2.5°, and the growth rate of falling speed decreases in later period. Change in door opening state has little impact on dropping displacement and pitch angle, but has greater impact on the yaw angle of missile. It shows that keeping the door away from missile as far as possible can effectively reduce the influence of the door, decrease the yaw angle and improve the separation quality.

fluid mechanics; buried weapon bay; bay door; weapon launch; overset mesh; improved delayed detached eddy simulation

2016-10-19

国家自然科学基金项目(11172283)

闫盼盼(1990—)，男，博士研究生。E-mail：09231190@bjtu.edu.cn

张群峰(1972—)，男，讲师，硕士生导师。E-mail：zhangqunfeng@263.net

V211.3

A

1000-1093(2017)06-1120-11

10.3969/j.issn.1000-1093.2017.06.011