存在动不平衡的旋转弹丸外弹道绕质心运动过程中引信惯性力分析

董盛鹏， 王雨时， 闻泉， 张志彪， 卢凤生， 刘锦春

(1.南京理工大学 机械工程学院, 江苏 南京 210094；2.黑龙江华安工业(集团)有限公司， 黑龙江 齐齐哈尔 161046)

存在动不平衡的旋转弹丸外弹道绕质心运动过程中引信惯性力分析

董盛鹏1， 王雨时1， 闻泉1， 张志彪1， 卢凤生2， 刘锦春2

(1.南京理工大学 机械工程学院, 江苏 南京 210094；2.黑龙江华安工业(集团)有限公司， 黑龙江 齐齐哈尔 161046)

为了给引信安全性和可靠性设计提供准确的外弹道力学环境，应用刚体动力学理论，建立了存在动不平衡角且引信轴线与弹丸旋转轴线不平行的旋转弹丸在外弹道上绕质心运动时引信所受惯性力数学模型，得到了引信零部件因弹丸绕质心运动产生的惯性加速度在轴向、径向和切向分量的计算公式。应用ADAMS软件仿真验证了理论分析的可信性。由受力分析可知，当引信轴向运动零部件质心、弹丸质心与各轴线在同一平面内，且引信轴向运动零部件质心与弹丸惯性主轴的距离最大时，引信轴向惯性力和径向惯性力均比传统计算结果大幅度增加(算例155 mm口径火炮达到数倍)。通过仿真引信轴向运动零部件的运动过程可知，在周期性波动且波动幅度较大的各向惯性力作用下，即使径向惯性力与切向惯性力远远大于轴向惯性力，也不能阻止引信轴向运动零部件在轴向惯性力作用下向前运动。

兵器科学与技术； 引信设计； 力学环境； 动不平衡弹丸； 弹道炸； 外弹道； 惯性力

0 引言

随着引信功能和结构越来越复杂，准确获得引信环境力及其对引信结构、机构和刚强度的影响，越来越成为引信安全性设计和可靠性设计的关键。弹丸在外弹道上的飞行运动可分解为弹丸质心运动与绕质心运动。就引信设计所关注的外弹道力学环境而言，弹丸绕质心运动所引起的惯性力峰值相比于弹丸质心运动所引起的惯性力更高，对引信外弹道安全性和可靠性的影响更大[1]。

在引信设计中，文献[2-4]给出了弹丸飞行过程中因弹丸绕质心运动而产生的作用于引信零部件上的惯性力计算公式，并且认为在弹丸绕心运动所产生的惯性力中仅有章动力对引信零部件轴向运动有影响。文献[5]定性提到弹丸进动和自转运动对引信零部件轴向运动也会产生影响，但并未做具体分析。文献[6]详细推导了旋转弹外弹道初始段引信环境力，得出了不能忽略旋转弹丸进动运动对引信轴向惯性力影响的结论,并由此提出“章进力”的概念，即弹丸绕质心运动使引信零部件受到的轴向惯性力包括章动运动产生的惯性力，也包括进动运动产生的惯性力。文献[7]提到弹丸动不平衡会使弹丸攻角增大，从而使引信轴向运动零部件因弹丸绕质心运动所产生惯性力增大。

传统引信设计在计算引信外弹道受力时，将弹丸视为绝对的轴对称体，没有考虑实际弹丸存在一定的不平衡特性(即弹丸极惯性轴线并不是其几何轴线)，也没有考虑轴向运动零部件实际运动轨迹与弹丸旋转轴线不平行的情况。此外，传统分析引信零部件的运动时往往只考虑各向惯性力极大值对引信的影响，这种基于静态或准静态的力学模型无法获得准确的引信机构动态响应结果。

在弹丸动不平衡以及引信轴向运动零部件实际运动轨迹与弹丸几何轴线不平行的情况下，研究旋转弹丸外弹道绕质心运动惯性力大小及其对引信的影响，可以为引信设计提供更为准确的外弹道环境，有助于避免弹道炸等安全事故的频繁发生，也有助于提高引信作用可靠性。

1 弹丸动不平衡与引信偏歪时引信轴向运动零部件惯性力理论分析

传统引信设计理论在计算旋转弹丸外弹道绕质心运动惯性力时，假设弹丸为绝对的轴对称体，其轴向运动零部件运动方向始终沿着弹丸几何轴线，详细推导过程参见文献[6-8]。从实际出发，考虑制造误差，本文对以下两种情形的旋转弹丸引信轴向运动零部件进行受力分析：

1)弹丸极惯性轴(即弹丸旋转轴)与弹丸几何轴线不重合，存在一定的夹角(即弹丸动不平衡角，此情形即为弹丸动不平衡)；

2)考虑弹丸与引信装配误差，或引信内部结构制造与装配误差导致的引信几何轴线与弹丸几何轴线不重合现象，则轴向运动零部件的运动方向与弹丸几何轴线还存在一定的夹角。

弹丸动不平衡与引信偏歪时引信轴向运动零部件受惯性力如图1所示。图1中：o、o′分别为引信轴向运动零部件质心和弹丸质心；直线l、直线p、直线q分别为引信几何轴线、弹丸几何轴线、弹丸极惯性轴；引信轴向运动零部件质心与弹丸质心轴向距离为n1；引信轴向运动零部件质心相对于引信几何轴线偏心量为n2；弹丸质心相对于弹丸几何轴线的径向偏移量(简称弹丸质偏)为n3；βD为弹丸动不平衡角；εi为引信几何轴线与弹丸几何轴线的夹角。坐标系oxyz固连于引信体(引信体坐标系)，ox始终平行于引信几何轴线，oy系引信轴向运动零部件质心相对于引信几何轴线的径向偏离方向，oz依据右手法则确定。坐标系ox′y′z′为弹轴坐标系，ox′平行于弹丸旋转轴线，oy′系引信轴向运动零部件质心相对弹丸旋转轴线的径向偏离方向，oz′依据右手法则确定。

图1 弹丸动不平衡与引信偏歪时引信轴向运动零部件的惯性力Fig.1 Inertia force of fuze axial moving parts for the projectile being dynamically imbalanced and the fuze being eccentric

引信体坐标系oxyz与弹轴坐标系ox′y′z′的相对方位关系如图2所示。图2中oxCyCzC为弹体坐标系，oxC始终平行于弹丸几何轴线，oyC系轴向运动零部件质心相对于弹丸几何轴线径向偏离方向，ozC依据右手法则确定。弹体坐标系oxCyCzC由弹轴坐标系ox′y′z′先绕oy′旋转βD1角、再绕ozC轴旋转βD2角得到，βD1和βD2为弹丸动不平衡角βD的两个分量。引信体坐标系oxyz由弹体坐标系oxCyCzC先绕oyC旋转εi1角，再绕ozC轴旋转εi2角得到，εi1和εi2为夹角εi的两个分量。设引信几何轴线与弹丸旋转轴线的夹角∠xox′=γ，∠yoy′=ξ，∠zoz′=ζ.

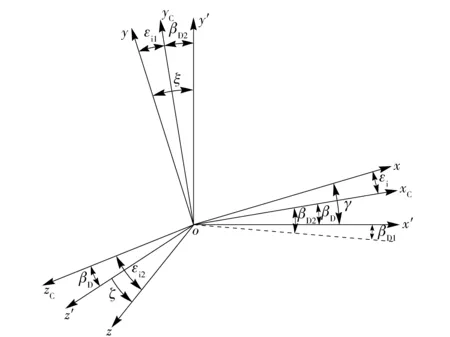
图2 各坐标系相对方位关系Fig.2 Relative position of each coordinate system

由受力分析可推导出引信轴向运动零部件沿坐标系ox′y′z′的各向加速度(具体推导过程与文献[6]中的基本一致)为

(1)

r=n1tanβDi+n2+n3+btanεij,

(2)

式中：b为引信轴向运动零部件质心距弹丸口部端面的距离；i、j为平面oyz内的单位向量。

由受力分析可知，引信轴向运动零部件沿引信几何轴线方向还要受到oy′和oz′方向的加速度分量。将ox′y′z′坐标系加速度转换到坐标系oxyz，可得引信轴向运动零部件沿坐标系oxyz的加速度为

(3)

式中：θ为平面ox′x与平面ox′y′组成的二面角，其值域为「-π,π⎤.

当n1、n2、βD和εi在同一平面即各偏心距与各轴线在同一平面上时，θ=0，此时γ可取得最大值γ=εi+βD；|r|为r的绝对值，则|r|可取的最大值为|r|max=n1tanβD+n2+n3+btanεi=r. 由于γ、ξ和ζ均较小，故可近似取sinγ=γ，sinξ=ξ，sinζ=ζ，cosγ=1，cosξ=1，cosζ=1. 由文献[2]可知a′Y≫a′Z，a′Y≫a′X. 当θ较小时，可忽略a′Z对aX的影响，当θ较大时，会导致|r|与γ的值较小，从而导致aX的值降低。因此若要得到aX的最大值，可近似取θ=0，此时oz′轴与oz轴重合，故∠z′oy、∠y′oz与∠x′oz均为π/2，∠x′oy=π/2+γ，|r|与γ均取得最大值，则(3)式可简化为

(4)

由此得到考虑弹丸动不平衡与引信偏歪时引信轴向运动零部件的动态惯性加速度计算公式。

2 弹丸动不平衡与引信偏歪时引信轴向运动零部件惯性力计算

针对外弹道起始段，对几何与力学上均为轴对称体的旋转弹丸求解绕心运动方程[6]得

(5)

(6)

(7)

将(5)式、(6)式和(7)式代入(1)式并简化可得沿坐标系ox′y′z′的各向加速度最大值为

(8)

将(8)式代入(4)式得惯性加速度沿坐标系oxyz即引信轴向、径向和切向的最大值为

(9)

以某155 mm口径远程杀伤爆破弹引信轴向运动零部件 ——“活机体”部件受惯性力计算为例，各计算参数如表1所列。将(1)式、(5)式、(6)式和(7)式代入(4)式计算，所得结果作为理论动态惯性加速度值。按(9)式计算，将结果作为理论静态值。再令r=n2+n3，按(8)式计算，计算结果为传统引信设计计算时的绕心运动惯性加速度值。针对上述3种情形，用MATLAB编程计算，不同最大攻角下对应活机体的各向惯性加速度最大值见表2所列，9°最大攻角时不同动不平衡角及引信轴线与弹丸轴线夹角条件下对应的活机体最大轴向加速度见表3.

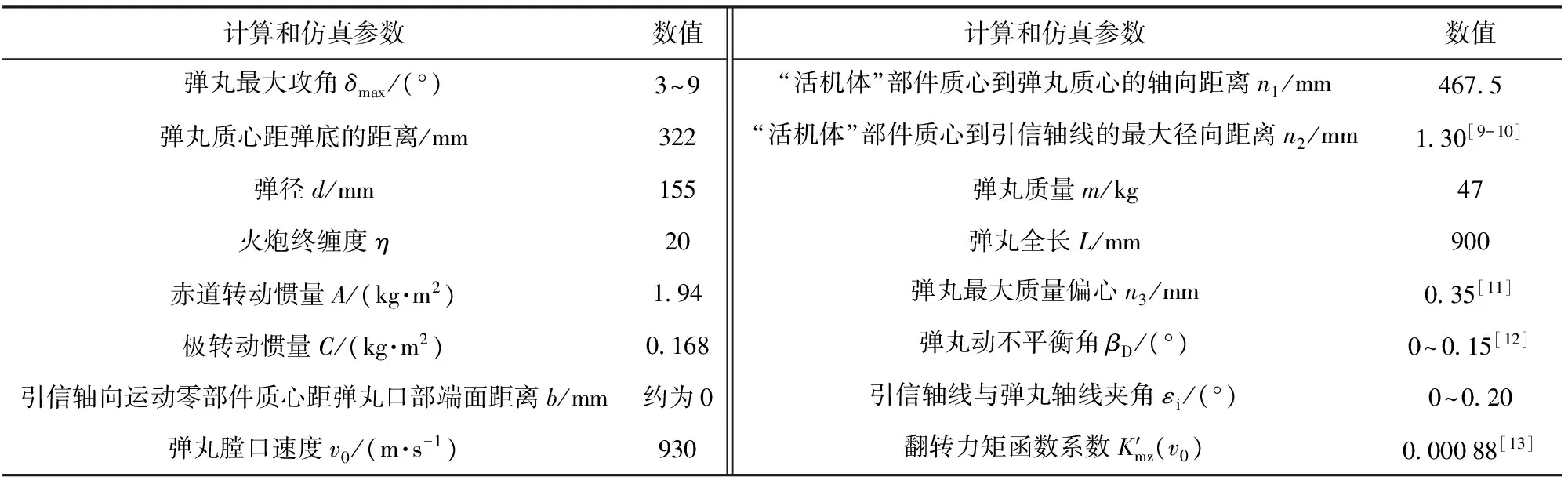
表1 某155 mm口径远程杀伤爆破弹丸引信轴向运动零部件惯性加速度计算用原始参数Tab.1 Parameter values for calculation of inertial acceleration of fuze axial moving parts of 155 mm caliber projectile

表2 某155 mm口径远程杀伤爆破弹丸不同最大攻角对应弹丸绕质心运动引信惯性加速度理论计算结果Tab.2 Calculated inertial accelerations of 155 mm caliber projectile moving around the center of mass at the maximum angles of attack

表3 不同动不平衡角及引信轴线与弹丸轴线夹角条件下对应的活机体最大轴向加速度

Tab.3 Axial acceleration of moving parts under the conditions of different dynamic unbalance angles and included angles m/s

2

由表2可知，本文理论推导的静态最大值与动态最大值非常接近，相对误差不超过1%，说明简化是合理的。而考虑弹丸动不平衡以及引信几何轴线与弹丸几何轴线不平行情况下所得引信零部件的轴向惯性加速度极值却要比传统计算值大很多(分别达到1.84倍和3.48倍)。

用MATLAB编程计算最大攻角为9°时极限条件下的各向惯性加速度变化规律如图3～图5所示。由图3～图5可知：各向加速度曲线均为周期性波动曲线，且波动幅度很大；径向加速度与切向加速度均远大于轴向加速度。

图3 9°最大攻角且考虑弹丸动不平衡与引信偏歪时弹丸绕质心运动产生的轴向惯性加速度Fig.3 Axial inertial acceleration due to the movement of projectile around the center of mass at 9°angle of attack when considering the dynamic unbalance of projectile and the eccentricity of fuze

图4 9°最大攻角且考虑弹丸动不平衡与引信偏歪时弹丸绕质心运动产生的径向惯性加速度Fig.4 The radial inertial acceleration due to the movement of projectile around the center of mass at 9°angle of attack when considering the dynamic unbalance of projectile and the eccentricity of fuze

图5 9°最大攻角且考虑弹丸动不平衡与引信偏歪时弹丸绕质心运动产生的切向惯性加速度Fig.5 Tangential inertial acceleration due to the movement of projectile around the center of mass at 9°angle of attack when considering the dynamic unbalance of projectile and the eccentricity of fuze

3 弹丸动不平衡与引信偏歪时引信轴向运动零部件惯性力仿真分析

弹丸绕质心运动可分解为章动运动、进动运动和自转运动，建立ADAMS仿真原理模型如图6所示。

图6 轴向运动零部件绕质心运动原理模型Fig.6 Principle model of motion of axial moving parts

图6中，o′为弹丸质心，o为引信轴向运动零部件质心，o′E为弹丸惯性主轴；Fo为引信轴向运动零部件实际运动方向，直线AB所指方向为弹丸速度方向。o′E在平面ABCD内绕弹丸质心o′作摆动运动，表示弹丸章动运动；o′E跟随平面ABCD绕线AB转动，表示弹丸进动运动；引信轴向运动零部件质心o绕o′E转动，其角速度为弹丸自转角速度。依据上述原理建立ADAMS仿真模型，可得引信轴向运动零部件o沿Fo方向(即实际轴向运动方向)惯性加速度。ADAMS仿真得到最大攻角为9°时引信轴向运动零部件轴向加速度曲线如图7所示。

图7 ADAMS仿真得9°最大攻角且考虑动不平衡特性与引信偏歪时弹丸绕质心运动产生的轴向惯性加速度Fig.7 Axial inertial acceleration due to the movement of projectile around the center of mass at 9°angle of attack when considering the dynamic unbalance of projectile and the eccentricity of fuze by simulation of ADAMS

对比图7与图3可知，仿真所得引信轴向运动零部件轴向加速度曲线与理论计算所得曲线规律基本一致，仿真所得引信轴向运动零部件轴向加速度最大值为284.2 m/s2，与理论推导所得最大值相差3.49%，二者相互验证，说明理论分析结果与仿真结果均是可信的。

4 弹丸绕质心运动各向惯性力对引信轴向运动零部件的影响

由计算和仿真结果可知，在弹丸动不平衡以及引信轴线与弹丸几何轴线不平行的真实情况下会使引信轴向加速度急剧增大，但同时也会增大径向加速度，从而增大轴向运动摩擦力，有可能阻碍轴向运动零部件的运动。下面以触发引信常见的的轴向运动零部件活机体受惯性加速度作用下的运动为例，分析各向惯性力以及摩擦力对引信轴向运动零部件的影响。建立活机体在延期装置中运动的ADAMS仿真模型，如图8所示，其中活机体与延期装置壳是最大配合间隙为0.37 mm的间隙配合，活机体材料为锌铝合金，延期装置壳为钢，二者之间在润滑下摩擦系数μ约为0.03～0.10[14]，在干摩擦状态下的摩擦系数约为0.17～0.20[14]，本文分别估取0.10和0.20，将图3～图5各向惯性加速度曲线导入仿真模型中，仿真得到活机体轴向速度和位移曲线如图9和图10所示。由图9和图 10可知，因径向力和切向力而产生的摩擦力在摩擦系数取0.10～0.20的情况下均不能完全阻止活机体的轴向运动。活机体仍能继续向前运动的原因可能是活机体与延期装置壳为间隙配合，且各向加速度波动幅度均较大，活机体与延期装置壳之间因振动和冲击而产生了周期性瞬时分离现象，活机体在瞬时分离时刻向前运动。从阶梯状位移曲线也可看出，活机体每隔一周期向前运动一小步，即活机体部件是“间歇性”地向前运动的，摩擦力未能阻止轴向运动件的运动。

图8 引信活机体运动仿真模型Fig.8 Motion simulation model of fuze axial moving parts

图9 μ=0.10时活机体速度曲线和位移曲线Fig.9 Velocity and displacement curves of axial moving parts for μ=0.10

图10 μ=0.20时活机体速度曲线和位移曲线Fig.10 Velocity and displacement curves of axial moving parts for μ=0.20

5 实用效果与试验结果说明

弹丸动不平衡与引信偏歪使引信轴向运动件轴向惯性力增大的本质性原因是：1)引信轴向运动零部件实际运动轨迹与弹丸旋转轴线存在夹角; 2)引信轴向运动零部件与弹丸旋转轴线的径向距离加大。传统引信轴向力计算公式已证明轴向运动零部件与弹丸旋转轴线的径向距离可以增大引信轴向运动件的惯性力。从引信轴向运动零部件实际运动轨迹与弹丸旋转轴线存在夹角方面进行外弹道环境力测试试验，可以证明本文的分析结论。通过改变螺纹的连接状态是简单而又有效地增大引信轴向运动零部件运动轨迹与弹丸旋转轴线夹角的方式，利用放置在引信传爆管部位的微小型全弹道加速度传感器和存储式测试系统，测得引信与弹丸在不同连接状态下的某76 mm口径舰炮榴弹射击时外弹道初始段引信轴向过载，如表4所示[15]。

表4 某76 mm舰炮榴弹弹引不同连接状态下 在炮口附近的轴向过载测试数据Tab.4 Measured axial overloads of 76 mm naval gun fuze

从表4可以发现，旋松状态下的引信轴向过载比紧固状态下的显著增大，故可知引信轴向运动零部件实际运动轨迹与弹丸旋转轴线的夹角可以增大引信轴向运动零部件的轴向过载。155 mm远程杀伤爆破弹丸的测试结果与此接近。本文研究结果与这些测试结论基本一致，说明是可信的。

6 结论

1) 建立了存在动不平衡角且引信轴线与弹丸旋转轴线不平行的旋转弹丸在外弹道上绕质心运动时引信受惯性力力学模型，得到了引信零部件因弹丸绕质心运动产生的惯性加速度在轴向、径向和切向的最大分量计算公式。通过ADAMS仿真验证了理论分析的可信性。由受力分析可知，当引信轴向运动零部件质心、弹丸质心与各轴线在同一平面内，且引信轴向运动零部件质心与弹丸惯性主轴距离最大时，除切向惯性加速度分量与传统引信工程设计计算值基本一致之外，所得轴向惯性力和径向惯性力均比传统计算值有大幅度增加。

2) 分析引信轴向运动零部件活机体部件惯性加速度计算结果与仿真所得其运动过程可知，各向惯性加速度呈周期性波动，且波动幅度较大，故即使径向惯性加速度与切向惯性加速度远远大于轴向惯性加速度，也不能阻止活机体在轴向惯性加速度作用下向前运动。

3)近年来频繁发生的弹道炸事故，可能与引信设计过程中未能考虑弹丸动不平衡角以及引信轴向运动零部件实际运动轨迹与弹丸旋转轴线不平行对引信轴向运动零部件惯性加速度的显著影响(分别达到1.84倍和3.48倍)，从而导致引信惯性发火机构意外前冲有关。在未能考虑弹丸动不平衡角以及引信轴向运动零部件实际运动轨迹与弹丸旋转轴线不平行对引信轴向运动零部件惯性加速度影响的理想状况下，单单试探性地增大弹道弹簧抗力，进退失据，难以确保设计改进有效与可靠。因此控制弹丸动不平衡角以及引信几何轴线相对于弹丸几何轴线的偏歪程度，并积累监测数据，对引信安全性设计和可靠性设计非常重要。

References)

[1] 王晓鹏，王雨时，闻泉，等. 非旋转弹外弹道绕质心运动引信受力分析[J]. 兵工学报，2015,36(1)：54-57. WANG Xiao-peng, WANG Yu-shi, WEN Quan, et al. Force analysis for the fuze on the motion of a unrotating projectile around the center of mass in exterior ballistics [J].Acta Armanemtarii, 2015,36(1)：54-57. (in Chinese)

[2] 《引信设计手册》编写组编. 引信设计手册[M]. 北京:国防工业出版社，1978. Compiling Team of Fuze Design Manual. The fuze design handbook [M]. Beijing: National Defense Industry Press, 1978. (in Chinese)

[3] 李占雄，郭占海，王叔来，等. GJB/Z135—2002. 引信工程设计手册[S]. 北京：中国人民解放军总装备部，2003. LI Zhan-xiong，GUO Zhan-hai，WANG Shu-lai，et al. GJB/Z135—2002 engineering design handbook for fuzes[S]． Beijing: the General Armament Department of the Chinese People’s Liberation Army，2003． (in Chinese)

[4] 触发引信教研室. 引信设计[M]. 北京：北京工业学院，1976. Trigger Fuze Teaching and Research Office . Fuze design [M]. Beijing: Beijing Institute of Technology, 1976. (in Chinese)

[5] 彭长清. 引信机构动力学[M]. 北京:兵器工业出版社，1994. PENG Chang-qing. Dynamics of fuze mechanism [M]. Beijing: Publishing House of Ordnance Industry, 1994. (in Chinese)

[6] 冯彦哲. 外弹道初始段引信力学环境分析[D]. 南京：南京理工大学，2008. FENG Yan-zhe．Analysis of mechanical environment for fuzes in the initial external trajectory [D]． Nanjing: Nanjing University of Science and Technology，2008． (in Chinese)

[7] 郭锡福. 火炮武器系统外弹道试验数据处理与分析[M]. 北京：国防工业出版社，2013. GUO Xi-fu. Data processing and analysis of the exterior ballistic test of artillery weapon system [M]. Beijing: National Defense Industry Press, 2013. (in Chinese)

[8] 浦发. 外弹道学(中册)：火炮弹丸的飞行稳定性理论[M]. 北京: 中国人民解放军总字150部队，1964. PU Fa． Exterior ballistics: part 2，the flight stability theory of projectiles[M]． Nanjing: Unit 150 of PLA，1964． (in Chinese)

[9] 闻泉，王雨时，陈会光. 引信机构旋转偏心的蒙特卡罗模拟[J]. 探测与控制学报，2007,29(3):72-79. WEN Quan，WANG Yu-shi，CHEN Hui-guang. Monte Carlo simulation of rotating eccentricity of fuze mechanism [J]. Journal of Detection and Control, 2007,29(3):72-79. (in Chinese)

[10] 倪庆乐，王雨时，闻泉，等. 基于三维造型的复杂形状零部件质心位置测量[J]. 兵器装备工程学报，2016，37(4)：66-68. NI Qing-le,WANG Yu-shi, WEN Quan, et al. Measurement of centroid position of complex shape parts based on 3D modeling [J]. Ordnance Equipment Engineering Journal, 2016, 37(4): 66-68. (in Chinese)

[11] 王晓鹏，王雨时，卢凤生，等. 155 mm口径火炮榴弹结构特征数分布特性研究[J]. 探测与控制学报，2015，37(5)：66-72. WANG Xiao-peng, WANG Yu-shi, LU Feng-sheng, et al. 155 mm caliber gun howitzer structure characteristic data distribution characteristics [J]. Journal of Detection & Control, 2015, 37(5): 66-72. (in Chinese)

[12] 刘福才，周长省. 弹箭动静不平衡度数字仿真方法[J]. 南京理工大学学报，1996，20(3)：237-240. LIU Fu-cai, ZHOU Chang-sheng.Numerical simulation method for dynamic and static unbalance of projectile and rocket [J]. Journal of Nanjing University of Science and Technology, 1996, 20 (3): 237-240. (in Chinese)

[13] 魏惠之，朱鹤松，汪东晖，等. 弹丸设计理论[M]. 北京：国防工业出版社，1985： 207-209. WEI Hui-zhi, ZHU He-song, WANG Dong-hui, et al. Projectile design theory [M]. Beijing: National Defense Industry Press, 1985:207-209. (in Chinese)

[14] 徐灏， 蔡春源， 严隽琪，等. 机械设计手册(第二卷)[M]. 北京：机械工业出版社，2000. XU Hao, CAI Chun-yuan, YAN Jun-qi, et al. Mechanical design handbook, second volume [M]. Beijing: China Machine Press, 2000. (in Chinese)

[15] 电子测试技术国防科技重点实验室. XXX机械触发引信环境力测试报告[R]. 太原：中北大学，2015. National Defense Laboratory of Science and Technology of Electronic Testing Technology. Environmental stress test report of XXX mechanical trigger fuze[R]. Taiyuan: North University of China, 2015. (in Chinese)

Inertia Force Analysis for Fuzein Motion of a Dynamic ImbalanceRotating Projectile around Mass Center in Exterior Ballistics

DONG Sheng-peng1， WANG Yu-shi1， WEN Quan1， ZHANG Zhi-biao1， LU Feng-sheng2， LIU jin-chun2

(1.School of Mechanical Engineering,Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China;2.Heilongjiang Huaan Industrial (Group) Limited, Qiqihar 161046, Heilongjiang, China)

In order to provide an accurate mechanical environment of exterior ballistics for the safety and reliability design of fuze, a mathematical model of the motion of rotating projectile, which has dynamic unbalance angle and the axis of rotation of fuze being umparallel to the axis of projectile, around the center of mess in exterior ballistics is established based on the rigid body dynamics. The formulas of the axial, radial and tangential components of inertial force acting on fuze parts, which is caused by the motion of rotating projectile around the center of mess, are derived. The credibility of the theoretical analysis is verified by the simulation of ADAMS software. It can be known from force analysis that, when the center of axial moving parts of fuze and the centroid of bullet and axis are on the same plane, and the distance between the centroid of axial moving parts of fuze and the inertia principal axis of projectile is maximum, the axial force and radial inertia force of fuze are greatly increased compared with the traditional calculation results (the inertia force of 155 mm caliber projectile achieves several times). The fuze axial moving parts can not be prevented from moving forward under the action of axial force even if the radial and tangential forces are far greater than axial force in the condition of periodic fluctuation and large fluctuation amplitude.

ordnance science and technology; fuzed design； mechanics environment； dynamic imbalance projectile； ballistic burst； exterior ballistics； inertia force

2016-08-23

董盛鹏(1991—)，男，硕士研究生。E-mail：845015679@qq.com

王雨时(1962—)，男，教授，硕士生导师。E-mail：wyshi204@163.com

TJ430.1

A

1000-1093(2017)06-1082-08

10.3969/j.issn.1000-1093.2017.06.006