某多管火箭武器射击密集度试验减少用弹量研究

于存贵， 梁晓扬， 朱志敏

(1.南京理工大学 机械工程学院, 江苏 南京 210094；2.湖北江山重工有限责任公司, 湖北 襄阳 441057)

某多管火箭武器射击密集度试验减少用弹量研究

于存贵1， 梁晓扬1， 朱志敏2

(1.南京理工大学 机械工程学院, 江苏 南京 210094；2.湖北江山重工有限责任公司, 湖北 襄阳 441057)

研究多管火箭炮非满管射击密集度试验方法及仿真技术，提出了一种新的减少多管火箭密集度试验用弹量的试验方法。基于虚拟样机的动力学仿真技术和多岛遗传算法(MIGA)理论，建立多管火箭炮发射动力学参数化仿真计算模型，将其集成在多学科优化设计软件ISIGHT框架中，采用MIGA作为优化控制策略，形成了基于等起始扰动偏差思想的多管火箭炮非满管装填射击密集度试验方案。对满管齐射和非满管连续射击方案的起始扰动和射击密集度进行仿真计算。仿真结果表明，两种方案起始扰动相同，系统密集度预测值满足F检验条件，证明提出的非满管装填射击密集度试验方案是完全可行的，形成的非满管连续射击密集度试验方案可减少试验用弹量41.7%.

兵器科学与技术； 多管火箭炮； 虚拟样机仿真； 多岛遗传算法； 非满管试验方法； 密集度； 等起始扰动偏差

0 引言

多管火箭炮管数较多时，一般通过采用非满管连射密集度试验替代满管火箭弹齐射密集度试验来进行密集度指标考核，这样可以减少试验用弹量，大幅节省试验费用。国家军用标准GJB8215—2014《火箭炮定型试验规程》[1]规定，火箭炮最大射程密集度试验采用非满管射击时，弹数为常温3组，高温、低温各1组。但非满管射击时每组选几发弹、其装填方式和射序如何确定却都没有说明。

芮筱亭等[2]依据自创的多体系统传递矩阵法，对多管火箭发射动力学理论、仿真技术等方面进行了深入研究。以其理论为基础，王国平等[3]应用随机整数规划方法，形成了减少多管火箭武器试验用弹量的数值仿真技术，对某40管火箭炮提出了7发连射的密集度试验方案；杨帆等[4]对某40管新型火箭炮提出了10发连射的密集度试验方案；张驰等[5]针对某19 管机载多管火箭，提出了6发连射的密集度试验方案。这些密集度试验方案都节省了大量试验费用，获得了较好效果。

目前，虚拟样机仿真技术在国防工业已得到普遍应用。本文基于虚拟样机的动力学仿真技术，建立多管火箭炮发射动力学参数化仿真计算模型；采用多岛遗传算法(MIGA)作为优化控制策略，将多管火箭炮发射动力学参数化仿真计算模型集成在多学科优化设计软件ISIGHT框架中，实现优化流程的自动进行。以装填方式和射序为变量，以非满管连射与满管齐射等起始扰动偏差为目标，通过大量计算、优化，确定了与满管齐射密集度相同的非满管装填连射试验方案，在保证试验质量的前提下大幅度减少了某多管火箭炮的密集度试验用弹量，并通过F检验验证了非满管连射试验方案的有效性。本文提出的非满管连续射击试验方法使某多管火箭炮密集度试验用弹量由60发弹(满管齐射常温、高温、低温各1组)减少到35发弹(非满管连射常温3组，高温、低温各1组)，比常规试验方法减少了41.7%，节省了大量试验费用。

1 问题的提出及研究思路

某20管122 mm轻型车载火箭炮是一种类似于美国高机动火箭炮系统(HIMARS)的高机动性多管火箭炮，由于底盘较轻、火箭炮总体结构变化很大，所以其射序、发射间隔和密集度试验方法都需要重新研究确定。通过典型管位火箭弹单发发射动力学分析和模态分析结果已确定了发射间隔；使用优化设计方法集成发射动力学分析已确定了射序(见图1)；根据减少试验用弹量的数理统计学原理[2,6]，为确保密集度估计值的置信度不低于91.7%，确定密集度试验用弹量为7发。这7发火箭弹的装填方式和射序是该轻型车载火箭炮密集度指标考核试验的关键技术问题。

图1 射序示意图Fig.1 Schematic diagram of firing orders

根据问题具体情况，本文主要是要寻找、确定连续发射的7发火箭弹的装填方式和射序，即能够满足与火箭炮按已定射序和发射间隔满管齐射方式等密集度的非满管发射试验方案，这种在有限集合上(20个管位)寻找满足条件的7个管位和顺序的问题，是一种典型的组合优化问题。对组合优化问题求解，遗传算法(GA)是众多求解策略中非常有效的一种[7]，是本文选择的优化控制策略。

GA模拟生物的遗传选择和自然淘汰进化机制，从一个初始种群出发，不断重复执行选择、交叉和变异操作，使种群进化越来越接近目标——“最适应环境”的个体，从而获得最优解或满意解。MIGA把一个大的种群分成若干个子种群(称之为“岛”)，而在每个岛上运用传统的GA独立地进行优化。不同岛屿上的个体定期进行随机“迁徙”，完成种群间个体的交换，增加个体的多样性。MIGA采用随机概率寻优的方法，具有更优良的全局求解能力和计算效率，有效地克服了传统GA容易出现早熟(找到局部最优点)现象的问题。

寻找与多管火箭炮系统满管齐射密集度相同的非满管连续射击试验方案，就是要通过对多管火箭炮任意发射方式发射过程的精确仿真，找到与满管齐射等起始扰动的非满管装填连续发射方式[5]，所以其核心是建立多管火箭炮参数化发射动力学仿真系统。

本文研究问题的具体技术途径为：以装填管位和射序为可变参数，建立基于虚拟样机技术的多管火箭炮参数化发射动力学仿真计算模型，并以其为核心；以多学科优化软件ISIGHT为总控框架，以MIGA为控制策略，控制优化流程，寻求与满管齐射等起始扰动偏差的非满管装填连续发射试验方案；最后用统计学方法检验两种方案的密集度估计值有无显著差异，最终找到用非满管连续射击代替满管齐射的多管火箭密集度试验方法。多管火箭炮减少试验用弹量的优化研究技术思路如图2所示。

图2 减少试验用弹量优化研究思路Fig.2 Optimization program of rocket consumption reduction

2 基于虚拟样机的参数化动力学仿真建模

对火箭炮进行发射动力学分析时，根据结构和运动情况将火箭发射系统划分为千斤顶、轮胎、车体、回转体、高低机、起落架(包括发射箱框架)、定向管和未发射的火箭弹等组成部分。并建立各部分的虚拟样机模型，对附属部分进行质量匹配，确保全炮质量、质心位置保持不变。火箭发射系统的拓扑结构如图3所示，其中定向管是玻璃钢材料，柔性效应较大，对火箭弹出管运动参数有一定的影响，因此建立为柔性体，其他部件按刚体处理。

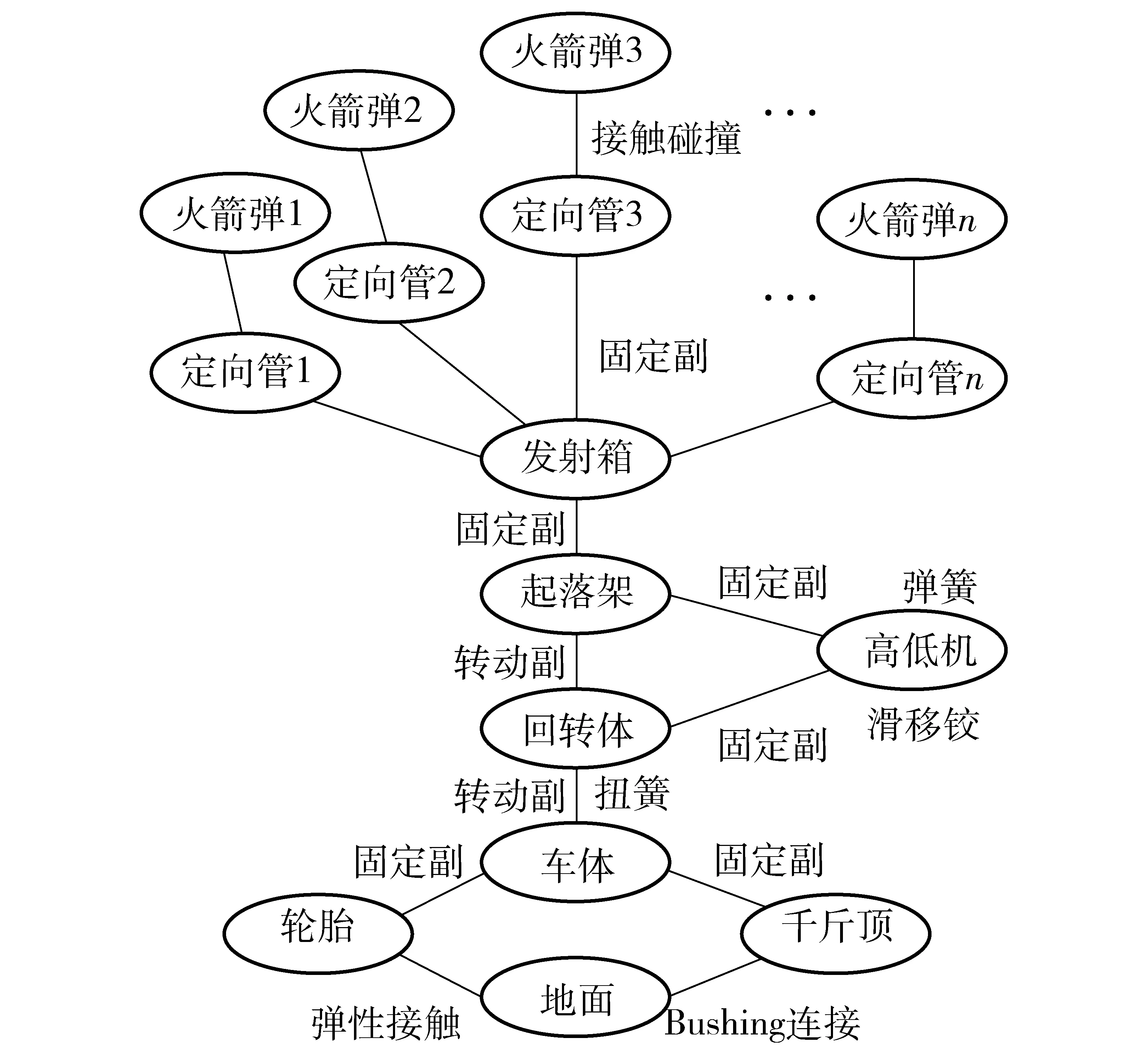
图3 发射系统的拓扑结构Fig.3 Topological structure of launching system

火箭炮的千斤顶和地面之间定义为Bushing连接，千斤顶本身简化为弹簧连接，施加刚度和阻尼；轮胎与路面之间的作用力通过调用系统自带的轮胎路面模型经修改参数后得到连接模型。回转体与底架之间用转动副来等效相对旋转运动，并在转动副上建立具有结构阻尼的扭簧等效方向受力。起落架和回转体之间设置绕耳轴转动的转动副，通过高低机作用使起落部分相对回转体转动。在高低机内筒、外筒之间添加滑移铰，并在内筒、外筒之间建立大刚度弹簧，以模拟高低机的作用。火箭炮高低机、方向机、千斤顶和轮胎等各处的刚度和阻尼参数根据样机试验测试数据得到。

火箭弹与定向器之间的运动通过接触碰撞进行约束。火箭弹与定向器之间的接触碰撞包括火箭弹定心部和定向器管壁及定向钮和螺旋导槽之间的接触碰撞，参数定义根据钢和玻璃钢材料之间的接触碰撞性质确定。

作用在火箭尾部的发动机推力采用试验测试数据，按照Akima拟合方式插值得到样条曲线函数，作用于火箭弹的尾部，其描述形式为

AKISPL(time-Var_j,0, SPLINE_tuili,0),

(1)

式中：time 为仿真分析的当前时间；Var_j为第j个火箭弹发动机点火的时间(也即第j个火箭弹开始发射的时间)；SPLINE_tuili是所需调用的实测火箭弹推力样条的名称，其曲线如图4所示。

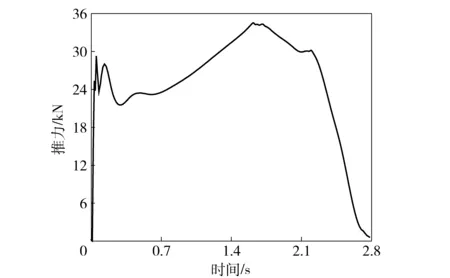
图4 作用在火箭上的推力Fig.4 Thrust applied on rocket

火箭采用零闭锁发射，点火之前火箭弹和定向器之间采用固定副连接。发射时，固定副失效。

火箭离开定向器管口后燃气流对火箭炮的冲击力由流体力学计算得到。将燃气流冲击力随时间变化的曲线加载到定向器管口部及发射箱前夹板。图5是第1发火箭弹离开定向器后对火箭炮的冲击力曲线图。

图5 1号管火箭发射时燃气流对发射箱冲击力曲线(从弹尾离开管口开始计时)Fig.5 Impact force of combustion-gas flow for Rocket 1 launching

非满管装填连续发射时，依据火箭弹装填管位和其周围迎气面大小来修正燃气流冲击力曲线。

动力学仿真模块中，用图1所示的定向管管序编号(满管齐射时的射序号)g1、g2、g3、…、g20作为参数。

非满管装填连续发射方案用装填管位和射序作为参数化变量，定义为

(2)

式中：x1、x2、…、x7的值是定向管的管序号。假定有一种非满管射击方案为：ci=(g2g4g9g7g12g14g18)，即表示在定向管g2、g4、g9、g7、g12、g14、g18(gi为管序号)中装弹，其他定向管不装弹。然后按g2—g4—g9—g7—g12—g14—g18的顺序发射。

非满管装填连续发射方案参数由优化控制模块生成，并传递给动力学分析模块。参数化动力学仿真模型保留相应管位的火箭弹，施加发动机推力和燃气流冲击力，并按优化控制方法定义的射序进行发射仿真。

同时将弹管间隙、发射间隔、弹质量偏差、质量偏心等参数处理为随机量，使仿真模型成为随机发射动力学仿真模型。

发射动力学仿真模型建立后利用多体动力学软件ADAMS的GSTIFF积分器来求解，求解过程如图6所示。

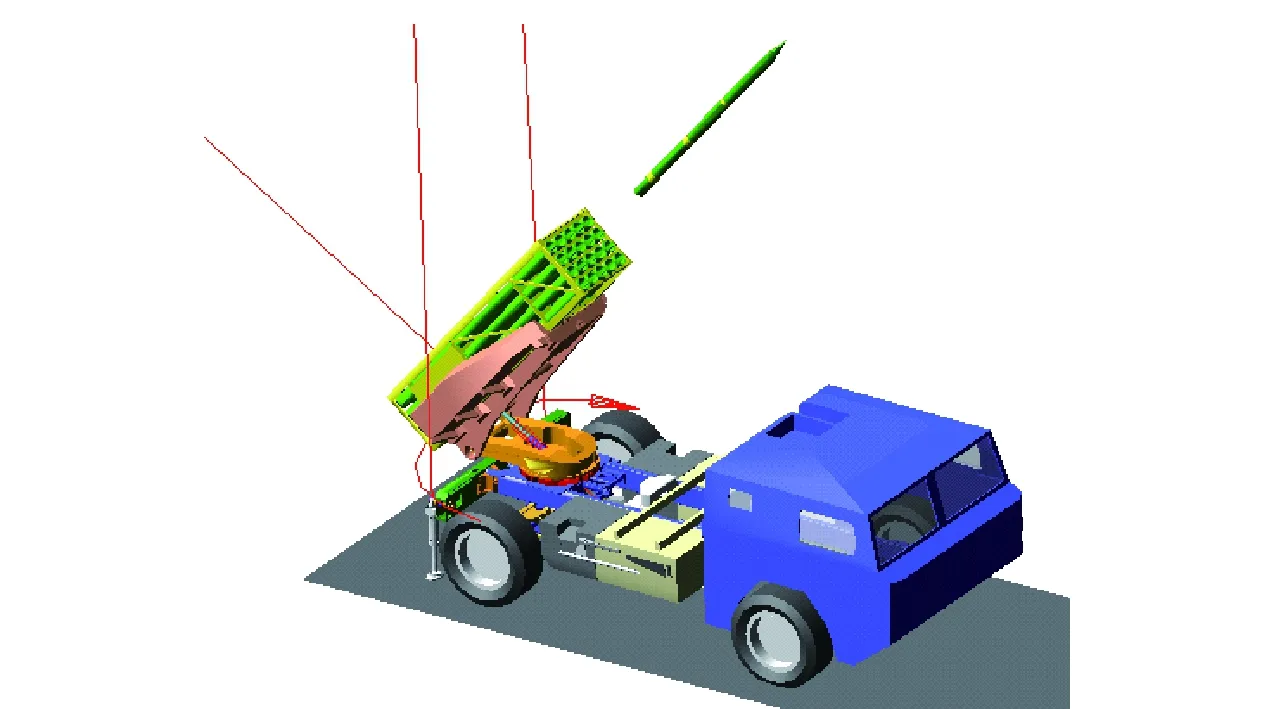
图6 火箭炮发射时动力学仿真过程Fig.6 Simulation of launching process

图7、图8为8号管单发发射定向器管口仿真曲线与试验测试结果，二者最大误差为4.8%，仿真计算结果与试验结果吻合较好，验证了动力学计算模型和所选参数的正确性。

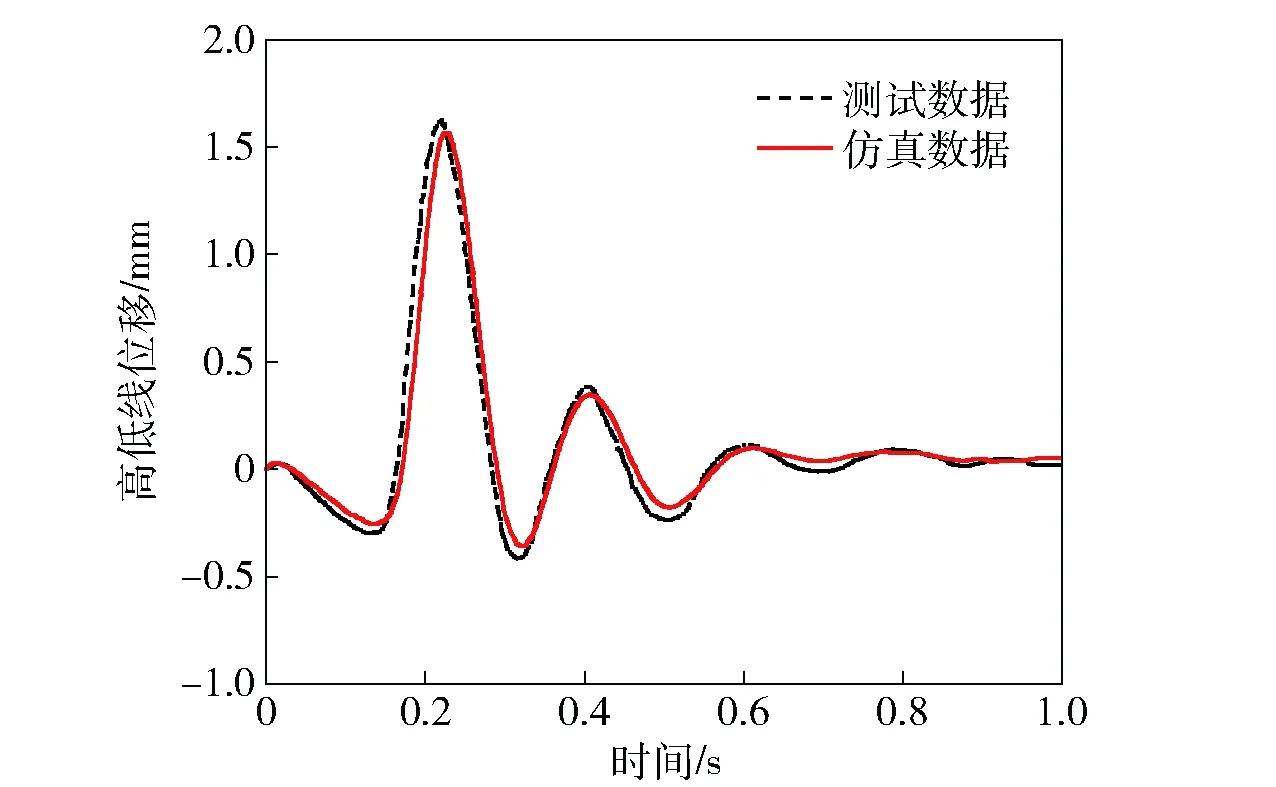
图7 8号管单发发射定向器管口高低线位移Fig.7 Simulated and test results of elevation displacement curve of launching guiders for Rocket 8 launching

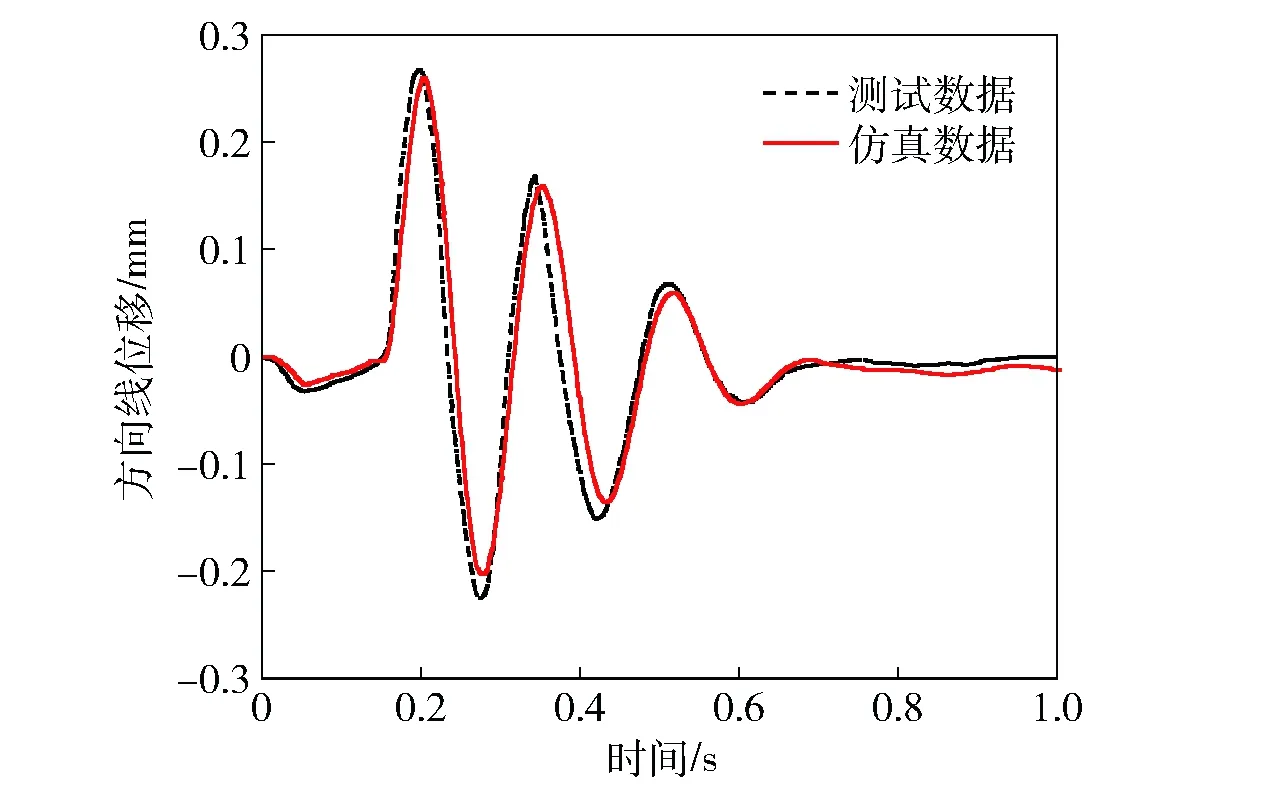
图8 8号管单发发射定向器管口方向线位移Fig.8 Simulated and test results of deflection displacement curve of launching guiders for Rocket 8 launching

根据确定的满管齐射射序和发射间隔进行满管齐射发射动力学计算，仿真计算得到发射过程中火箭炮振动曲线，定向器管口的高低角速度、角位移和方位角速度、角位移等振动时间历程曲线如图9～图12所示。根据文献[8]算出满管齐射时的起始扰动中间偏差，作为非满管连续发射时的优化目标。

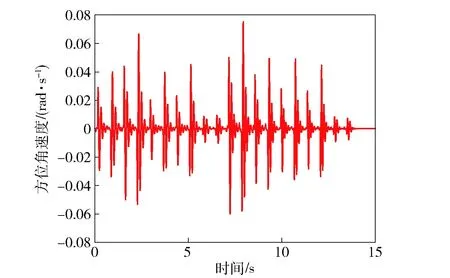
图9 方位角速度变化时间历程Fig.9 Deflection angular velocity curve of launching guiders

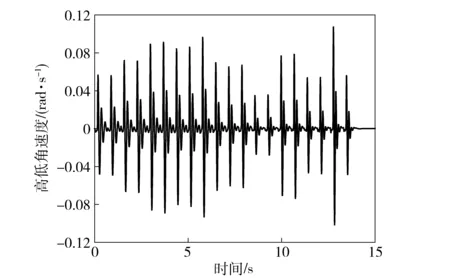
图10 高低角速度变化时间历程Fig.10 Elevation angular velocity curve of launching guiders

图11 方位角位移变化时间历程Fig.11 Deflection angular displacement curve of launching guiders

图12 高低角位移变化时间历程Fig.12 Elevation angular displacement curve of launching guiders

3 减少试验用弹量优化建模与分析

3.1 编码方案

GA最开始的工作是编码——把问题的参数或变量转化为遗传中的染色体或者个体，形成初始种群，然后进行选择、交叉和变异的操作。

火箭炮按满管齐射射序排列可得到次序表W=(1，2，3，…，20)，每根定向管用其射序号作为标识，称为管序号。非满管射击方案就用这些管序号进行排列。参照文献[9-10]，非满管射击方案中的相应变量可以用定向管的管序号作为编码方案，但是因为一个方案中定向管不能多次装填发射，即非满管射击方案中不能同时出现两个或多个相同的管序号，所以采用净排序号——即动态次序表W′(去掉射击方案中当前已选定的管序号)中的排序号作为编码方案。如非满管射击方案c=(g2g4g9g7g12g14g18)的净排序号，即编码串为T=(2 3 7 5 8 9 12).

3.2 优化模型建立

发射动力学理论与射击试验表明，影响多管火箭密集度的因素主要有：火箭弹的起始扰动、火箭弹自身因素(如火箭弹质量偏心、推力偏心等)、气象条件(主要是阵风等)等。对同一批次性能稳定的火箭弹，火箭弹的各种因素对满管齐射和非满管连射两种情况的密集度影响程度基本一样。所以，造成同一多管火箭炮满管齐射与非满管连射密集度差别大的主要原因是两种发射情况下火箭弹起始扰动的差别。因此，在减少多管火箭试验用弹量问题研究中，应用多体系统发射动力学，以控制装填方式和射序的非满管射击方案与满管齐射的火箭起始扰动偏差相同为原则寻求非满管射击试验方案。

目标函数：

minE=(EF7-EF20)2+(EG7-EG20)2,

(3)

式中：EF7、EG7分别为非满管装填7发火箭弹连续射击的纵向和方向起始扰动中间偏差；EF20、EG20分别为满管齐射时的纵向和方向起始扰动中间偏差。

设计变量：

yj为整数(j∈[1,7]),

(4)

(5)

3.3 优化模型参数设置

3.3.1 种群初始化

优化流程开始执行时，首先根据问题具体要求及约束条件采用随机数字产生方法生成若干个初始方案的编码串，使种群初始化。本问题优化计算中设置种群/岛的个数为10，每个种群大小为50.

种群初始化产生的每个编码串都是一个非满管装填连续射击方案。系统根据编码原则，对每个编码串进行解码，变成非满管装填连续射击的管位和射序，调用参数化动力学仿真模型，计算火箭炮采用该装填方案连续发射时的起始扰动中间偏差和目标函数值。

3.3.2 计算种群的适应度

GA中是以个体适应度的大小来评定种群中个体的优劣程度，度量适应度的函数称为适应度函数。为了增大适应度值较高个体与其他个体的差距，增强被选择遗传的概率，适应度函数选择指数函数形式[11-12]，可表示为

f=Ce-E,

(6)

式中：f为适应度值；C为常数；E是非满管射击试验方案的目标函数值。

根据确定的适应度函数，与满管齐射起始扰动差值越小的方案有较大的适应度值，从而在遗传操作过程中，其个体遗传到下一代的概率较大。

3.3.3 产生新的种群

1) 选择

个体的适应度值求出后，采用比例选择法计算出个体的适应度值在群体适应度值总和中所占的比例，即表示该个体在选择过程中被选中的概率。

比例选择算子以正比于个体适应度值的概率来选择相应的个体，设群体大小为M，个体i的适应度值为fi，则个体i被选中的概率pi[12]为

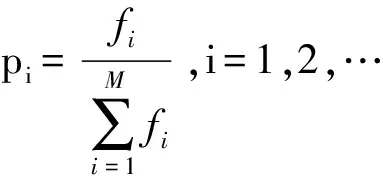
(7)

2) 交叉

根据确定的选择机制，选取种群中适应度较好的方案为双亲作基因链码的交叉，产生新的方案作为他们的后代。交叉方法是：随机地选取一个截断点，将双亲的基因链码在截断点切开，根据交叉概率Pc进行交叉操作。一般建议Pc为0.4～0.99[12]，计算中取值0.8.

3) 变异

变异操作可以防止出现未成熟收敛现象，增加种群的多样性。变异方法是：交叉结束后使种群中各方案编码位串上的数字按变异概率Pm随机改变，这样通过改变编码位上的数字使得其方案与原方案有所不同。一般建议变异概率Pm为0.000 1～0.1[12]，计算中取值0.01.

4) 迁徙

MIGA每隔一定的代数，会按一定的比例选择各岛的个体，转移到其他岛上。控制岛群间迁徙的参数为岛间迁移率和迁移的间隔代数，岛间迁移率是各岛之间进行种群交换的比率，一般建议在0～0.5之间取值，计算中取值0.1，迁移的间隔代数取值为5.

3.3.4 结束条件

根据种群的平均适应度和遗传代数作为优化搜索结束的条件，当种群的平均适应度没有明显变化或者遗传代数(本次计算时选取5 000)过大时，就结束优化计算，将当前群体中的最佳个体作为非满管连续射击问题的最优方案输出。

3.4 优化流程及结果

基于ISIGHT软件建立的减少试验用弹量优化流程如图13所示。

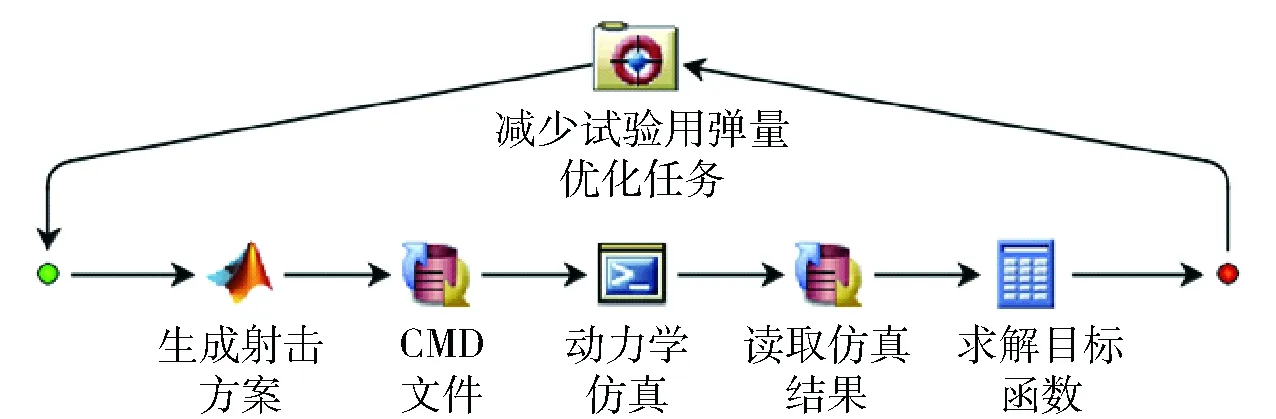
图13 减少试验用弹量优化流程图Fig.13 Flow chart of optimization program of rocket consumption reduction

1)生成射击方案：根据ISIGHT软件生成、传递过来的设计变量xi(i=1，2，3，4，5，6，7)，解码计算得到该方案装弹的管位号，不装弹的管位赋值为0；

2)CMD文件：根据确定的装弹管位号及顺序，改写ADAMS计算文件中管位DV_i的对应值，使装填管位和射序改变为当前确定的试验方案，不装弹定向管内的火箭弹失效；

3)动力学仿真：后台调用参数化动力学仿真模块进行计算分析，输出仿真结果；

4)读取仿真结果、求解目标函数：读取动力学仿真后输出的数据，并计算各方案的起始扰动中间偏差值；

5)减少试验用弹量优化任务：ISIGHT软件利用MIGA对整个过程进行控制，并计算各方案目标函数值，寻找最优解。

设置仿真模型各运行参数后，启动优化流程，经4 300次迭代运算后，得非满管装填连续射击试验方案如图14所示。

图14 优化得到的非满管装填试验方案Fig.14 A test scheme for non-full loading

4 多管火箭非满管射击试验方案确定

应用基于虚拟样机的参数化随机动力学仿真模型，对某多管火箭炮20发满管齐射进行发射动力学计算，得到火箭起始扰动偏差；根据文献[13]考虑起始扰动、发动机推力、推力偏心、质量、质量偏心、气动偏心和阵风等随机因素的6自由度刚体弹道模型，编制火箭外弹道计算程序，采用蒙特卡洛法进行仿真计算，得到满管齐射的密集度估计值，并与试验结果进行对比。仿真与试验结果如表1所示。

表1 满管齐射最大射程密集度仿真与试验结果Tab.1 Simulated and test results of firing dispersion for full loading firing with maximum rang

表1中EX/X为纵向密集度，EZ/X为横向密集度，EX、EZ分别为落点的距离中间偏差和方向中间偏差，X为火箭弹的最大射程。从表1可以看出，仿真值和试验值吻合较好，再次验证了仿真系统的准确性。

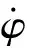
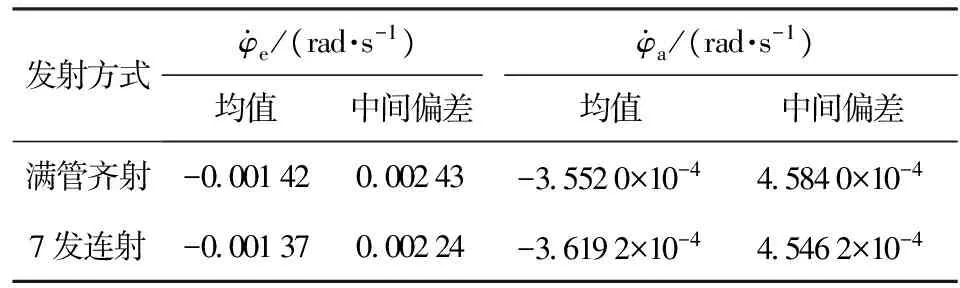
表2 火箭起始扰动仿真统计结果Tab.2 Statistical results of simulation test for rocket initial disturbance

从表2可以看出，满管齐射与7发连射的起始扰动仿真结果趋于一致，说明两系统火箭弹起始扰动相同，保证了非满管射击替代满管齐射密集度试验方案的可行性。

将外弹道计算程序与参数化随机发射动力学仿真模型集成，形成随机发射和外弹道仿真计算模型。对该多管火箭炮满管齐射和7发连射进行随机发射动力学计算，得到火箭起始扰动；采用蒙特卡洛法进行火箭外弹道仿真计算，对两种射击方案的密集度进行仿真预测。图15、图16分别是7发连射方案和满管齐射方案的中间偏差值随仿真组数的变化，及满足F检验的允许范围的仿真结果。

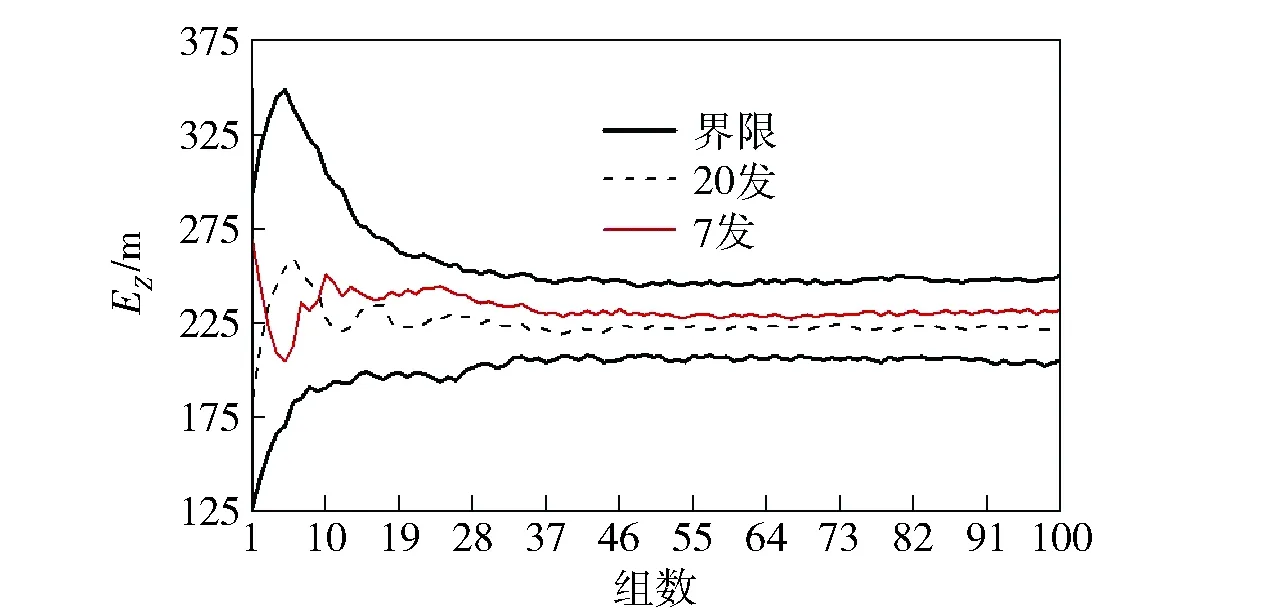
图15 7发连射与满管齐射方向中间偏差估计值随仿真实验组数的变化Fig.15 Estimated values of intermediate deviations of dispersion direction in test groups of 20 tubes and 7 tubes

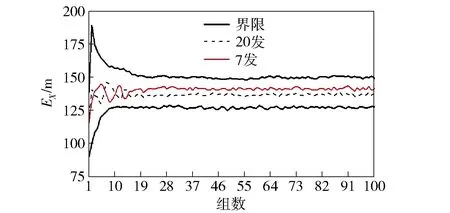
图16 7发连射与满管齐射距离中间偏差估计值随仿真实验组数的变化Fig.16 Estimated values of intermediate deviations of dispersion distances in test groups of 20 tubes and 7 tubes

从图15、图16中可以看出，两种方案的中间偏差值始终满足F检验的要求并随仿真实验组数增加逐渐趋于一致，说明两种方案的射击密集度相同，表明通过优化得出的某轻型火箭炮非满管射击试验替代满管齐射进行密集度试验是完全可行的。

5 结论

本文应用基于虚拟样机的动力学仿真技术和MIGA理论，建立了多管火箭炮发射动力学参数化仿真计算模型，将其集成在多学科优化设计软件ISIGHT框架中，采用MIGA作为优化控制策略，形成了基于等起始扰动偏差思想的多管火箭炮非满管装填射击密集度试验方案。对满管齐射和非满管连续射击方案的起始扰动进行了仿真计算，对其射击密集度进行了仿真预测。仿真结果表明，两种方案起始扰动偏差相同，保证了非满管射击替代满管齐射密集度试验方案的可行性；系统密集度预测值满足F检验条件，证明提出的非满管装填射击密集度试验方案是完全可行的。

本文形成的非满管连续射击密集度试验方案可减少试验用弹量41.7%，节省大量试验费用。本方法可推广应用于其他多管火箭武器密集度试验中。

References)

[1] 中国人民解放军总装备部. GJB 8215—2014火箭炮定型试验规程[S]. 北京：中国人民解放军总装备部，2015. PLA General Armament Department.GJB 8215—2014 Approval test operation procedure for rocket launcher[S]. Beijing：Military Standard Publishing Department，General Armament Department, 2015. (in Chinese)

[2] 芮筱亭, 陆毓琪, 王国平, 等. 多管火箭发射动力学仿真与试验测试方法[M]. 北京: 国防工业出版社, 2003:184-215. RUI Xiao-ting, LU Yu-qi, WANG Guo-ping, et al. Simulation and test methods of launch dynamics of multiple launch rocket system[M]. Beijing：National Defense Industry Press，2003:184-215.(in Chinese)

[3] 王国平, 芮筱亭, 陈卫东, 等. 减少多管火箭武器试验用弹量仿真技术[J]. 兵工学报, 2004, 25(6)：786-789. WANG Guo-ping, RUI Xiao-ting, CHEN Wei-dong, et al. Simulation in the reduction of rocket consumption in multiple launch rocket system tests[J]. Acta Armamentarii， 2004，25(6)：786-789.(in Chinese)

[4] 杨帆, 芮筱亭, 王国平, 等. 非满管射击密集度试验方法[J]. 南京理工大学学报，2009，33(1)：83-87． YANG Fan, RUI Xiao-ting, WANG Guo-ping, et al. Test method of non-full loading firing dispersion[J]. Journal of Nanjing University of Science and Technology，2009，33(1)：83-87.(in Chinese)

[5] 张驰, 芮筱亭, 戎保, 等. 机载多管火箭非满管射击试验方法研究[J]. 振动与冲击，2013，32(2)：1-5. ZHANG Chi，RUI Xiao-ting, RONG Bao, et al. Test method of non-full loading firing dispersion for an airborne multiple launch rocket system[J]. Journal of Vibration and Shock，2013，32(2)：1-5.(in Chinese)

[6] 姚志军. 多管火箭射击精度试验方法研究[D]. 南京：南京理工大学，2008:67-68. YAO Zhi-jun. Firing accuracy test method of multiple launch rocket system[D]. Nanjing:Nanjing University of Science and Technology，2008:67-68.(in Chinese)

[7] 马立肖, 王江晴. 遗传算法在组合优化问题中的应用[J]. 计算机工程与科学，2005，27(7)：83-87． MA Li-xiao, WANG jiang-qing. Application of genetic algorithms in solving the optimal combination problem[J]. Computer Engineering & Science，2005，27(7)：83-87.(in Chinese)

[8] 李军, 马大为, 曹听荣，等. 火箭发射系统设计[M]. 北京: 国防工业出版社, 2008:167-169. LI Jun，MA Da-wei，CAO Ting-rong,et al. Design of rocket launching system[M]. Beijing：National Defense Industry Press， 2008:167-169.(in Chinese)

[9] 唐文艳. 结构优化中的遗传算法研究和应用[D]. 大连：大连理工大学, 2002:55-60. TANG Wen-yan. Research and application of genetic algorithm in structural optimization[D]. Dalian:Dalian University of Technology，2002:55-60.(in Chinese)

[10] 刘来君，倪富陶，孙维刚，等. 多段交叉遗传算法在连续刚构桥测点优化中的应用[J]. 重庆交通大学学报:自然科学版，2016，35(2):6-9. LIU Lai-jun，NI Fu-tao，SUN Wei-gang，et al. Application of multistage crossing genetic algorithms by optimal sensor placement in dynamic test of continuous rigid frame bridge [J]. Journal of Chongqing Jiaotong University:Natural Science，2016，35(2)：6-9.(in Chinese)

[11] 黄志望. 改进遗传算法及其在结构工程优化中的应用研究[D].北京： 北京工业大学，2005:34-38. HUANG Zhi-wang. Improved genetic algorithm and its application and research in structural engineering optimization[D].Beijing: Beijing University of Technology，2005:34-38.(in Chinese)

[12] 李明. 遗传算法的改进及其在优化问题中的应用研究[D]. 长春：吉林大学，2004:9-14. LI Ming. The study on improved genetic algorithm and its application in optimization questions[D]. Changchun:Jilin University， 2004:9-14.(in Chinese)

[13] 徐明友. 火箭外弹道学[M]. 哈尔滨：哈尔滨工业大学出版社，2004:4-57. XU Ming-you. Rocket exterior ballistics[M]. Harbin：Harbin Institute of Technology Press，2004:4-57. (in Chinese)

Research on the Rocket Consumption Reduction in MultipleLaunch Rocket System Test

YU Cun-gui1，LIANG Xiao-yang1，ZHU Zhi-min2

(1.School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，Jiangsu，China；2.Hubei Jiangshan Heavy Industries Company Limited, Xiangyang 441057，Hubei，China)

The test method and simulation technology about the non-full loading firing dispersion for multiple launch rocket system (MLRS) are studied. A new method for reducing the rocket consumption in dispersion test of MLRS is presented. A parameterized simulation model of MLRS is established by use of the virtual-prototype-based dynamics simulation technology and multi-island genetic algorithm. The proposed model is integrated in the multidisciplinary optimization software ISIGHT. Based on the idea of equal initial disturbance deviation, a firing dispersion test method of a non-full loading MLRS is presented by using the multi island genetic algorithm as the optimization control strategy. The initial disturbance and firing dispersion are calculated via simulation in the case of full loading salvo and non-full loading continuous fire. The simulated results show that the two schemes have the same initial disturbance, and the system firing dispersion is satisfied with F test, which proves that the proposed firing dispersion test method with the non-full loading for MLRS is completely feasible. The rocket consumption in firing dispersion test of a MLRS can be decreased by 41.7% using the proposed non-full loading scheme.

ordnance science and technology; multiple launch rocket system; virtual prototype simulation; multi-island genetic algorithm; test method with non-full loading; firing dispersion; equal initial disturbance deviation

2016-10-11

于存贵(1965—)，男，副教授，硕士生导师。E-mail:yu_cungui@sina.com

TJ393

A

1000-1093(2017)06-1067-08

10.3969/j.issn.1000-1093.2017.06.004