波浪作用下管道冲刷暴发计算的边界元方法

夏华永,王俊勤

(1.国家海洋局南海预报中心,广东广州510300; 2.中海石油(中国)有限公司北京研究中心,北京100027)

波浪作用下管道冲刷暴发计算的边界元方法

夏华永1,王俊勤2

(1.国家海洋局南海预报中心,广东广州510300; 2.中海石油(中国)有限公司北京研究中心,北京100027)

管道冲刷暴发临界条件是海底管道设计和运营的重要参数。Sumer等给出了3个Keulegan-Carpenter (KC)数的波浪作用下冲刷暴发的试验曲线。但对于任意KC数,Sumer等的方法并不准确。因此,建立波浪作用下冲刷暴发条件计算方法,具有重要意义。因管道与床面相交形成了复杂的几何形状,管道与床面的交叉点是数值奇点,因而管道冲刷暴发临界条件计算较为复杂。本研究采用边界元方法计算波浪运动及渗流压力。边界元可准确地拟合海底与管壁边界,方便地处理管道与海床交叉点的数值奇点问题,并可直接计算出奇点处的垂向压力梯度,准确地计算冲刷暴发的临界条件。本研究计算结果与实测值符合良好。

海底管道;冲刷暴发;边界元;数值奇点

海底管道悬空是管道运行极大的安全隐患,因此,管道局部冲刷是管道设计与运行必需掌握的参数。目前,已发展了多种海底管道冲刷模型,如势流模型、大涡模拟模型、紊流模型、涡度模型、两相流模型及格点波尔兹曼方法模型[1-6]。模拟过程中,这些模型都假定管道下面与海床之间已有一个小的缝隙,即假定了管道冲刷已经发生,然后模拟在水流与波浪作用下的海床冲刷过程及平衡剖面形态。但是,铺设在海底的管道在其自重作用下会发生一定程度的自埋,管道是否会发生冲刷呢?这需要首先计算其冲刷暴发的临界条件。

目前,对于管道冲刷暴发的机制与临界条件,已有多种试验研究[7-11]。试验结果已揭示了冲刷暴发的机制,确定了冲刷暴发的判别条件,建立了冲刷暴发的计算方法。试验表明,管道上游涡旋与管道下面渗流的联合作用是冲刷暴发的原因,后者起主要作用。管道与海床的下游交叉点处,渗流垂向压力梯度大于泥沙浮重时,产生管涌,冲刷暴发。Sumer等[11]根据试验资料,整理了冲刷暴发临界条件的计算方法,单向流作用下,给出了冲刷暴发临界条件的经验公式,计算方便,对于波浪作用下冲刷暴发的临界条件,则给出了3个Keulegan-Carpenter(KC)数的图示曲线,可根据图示曲线得到临界条件。

对于冲刷暴发临界条件的模型计算,就本文作者所知,只有极少的研究成果。杨兵等[12]模拟分析了管道周围水体及渗流的压力分布,重现了管道冲刷的暴发机制。Liang和Cheng[13],Zang等[14]建立模型,模拟计算了单向流与波浪作用下的管道冲刷暴发的临界条件。管道轻微埋在海床上,在管道与海床的交叉点形成了复杂的几何形状。冲刷暴发计算需要处理好这一复杂的边界,而且处理好这些边界对流场及压力模拟非常重要,特别是在交叉点。结构网格很难处理好这一几何形状。非结构网格可以处理这一边界。但是,在渗流计算中,交叉点是渗流压力梯度的奇异点,差分法与有限元法都难于计算交叉点的垂向压力梯度,因而也影响冲刷暴发临界的预测精度。Liang和Cheng[13],Zang等[14]都通过建立下游交叉点处渗流垂向压力梯度与两个交叉点之间平均压力差之间的关系,进一步计算冲刷暴发的临界条件。

目前,冲刷计算一般采用Navier-Stokes方程,嵌入紊流封闭子模型提供参数化方案。渗流的控制方程则为Laplace方程。但是,波浪运动通常当作势流来处理。势流与渗流都可以准确地用边界元方法计算。对于Laplace方程,边界元法是一种非常有效的计算方法[15]。边界元具有准确拟合边界,降低计算维数,大幅度的减小计算量、可得到精确解、达到任意分辨率等优势。边界元法可以处理奇点问题,给出交叉点准确的渗流垂向压力梯度。对于任意KC数下临界冲刷条件,Sumer等[11]建立的图示并不能方便的给出。建立简单而准确的波浪作用下冲刷暴发临界条件的计算方法,有其明确的应用价值。

(李 燕 编辑)

1 冲刷暴发机制

Sumer等[11]对波流作用下的管道冲刷暴发机制已做了全面的总结,为了论文完整性,对冲刷暴发临界条件在此简单介绍一下。海底铺设了管道后,改变了局部的流态,流态的改变导致管道附近水体及床面上的压力变化。床面的压力分布不均匀及管道对渗流结构的影响导致了管道下沙体较大的压力梯度存在(图1)。图1中,管道直径为D,管道埋入海床的深度为e,B点与A点分别为管道与海床的上、下游交叉点。当在管道下游管壁与床面的交叉点(图1中的A点)的垂向压力梯度大于沙土水下重量时,管道冲刷暴发

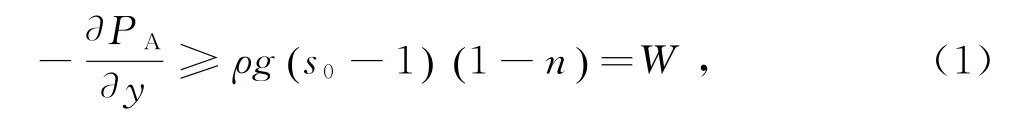
式中,PA为交叉点A处渗流压强;s0=ρs/ρ,ρ为海水密度,ρs泥沙密度;n为沙体的孔隙率;g为重力加速度;W为泥沙的水下重量。

Zang等[14]取渗流出流点A处的垂向压力梯度与管道下方的平均压强相关

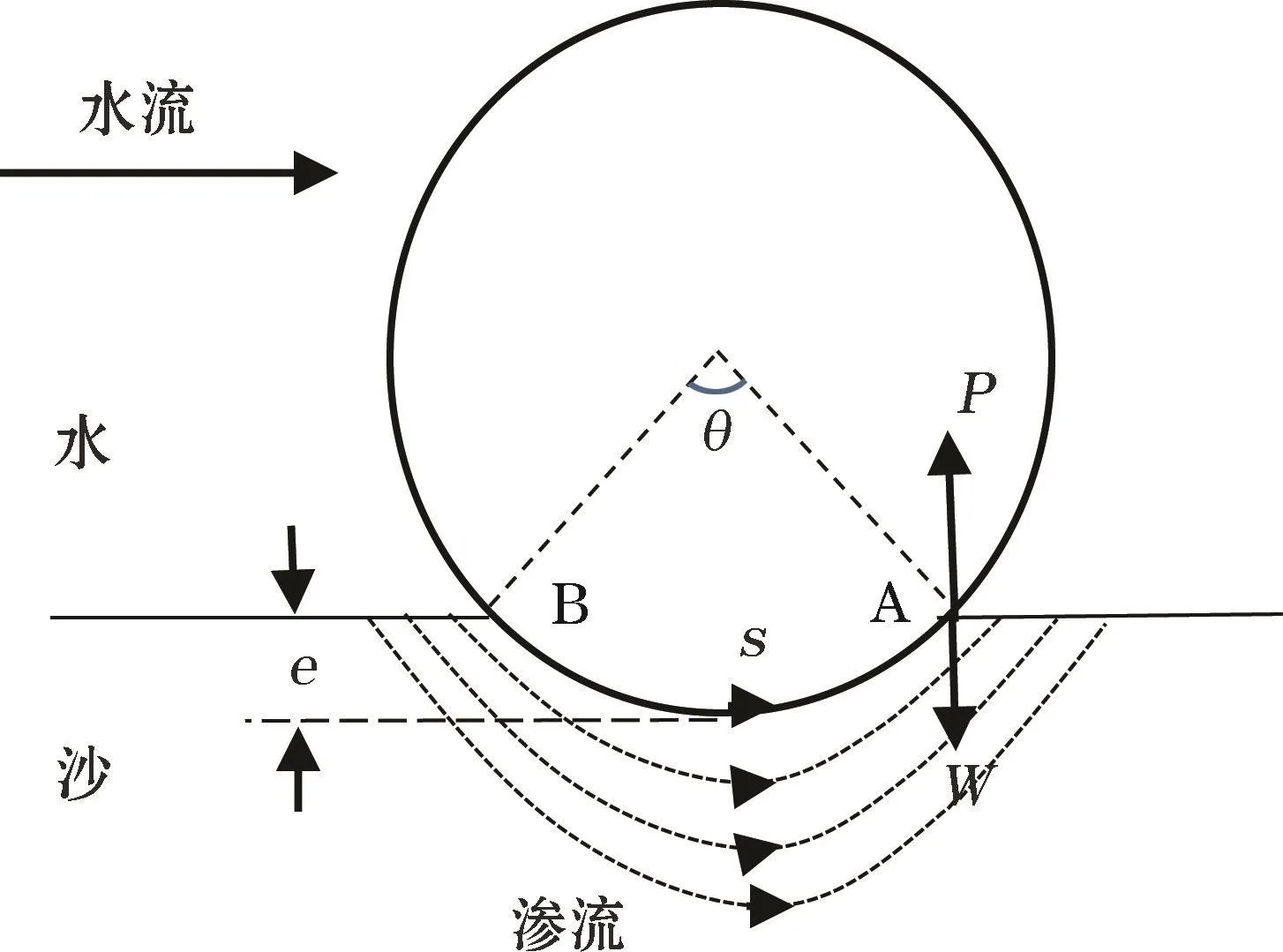
图1 管道下渗流分布示意图Fig.1 A sketch of seepage flow distribution beneath the marine pipeline

式中,λA是一个校正系数;s是沿管壁距离。试验结果显示,管道下渗流压强变化剧烈,因此,λA是一个变化复杂的系数。取管壁下平均压强为

式(3)中,D为管道直径;u0为海底未受扰动时的流速;ΔCP0为A,B两点之间的压力降幅系数,CPA,CPB为压力系数。由式(1)～式(3),得到冲刷暴发条件的替代表述

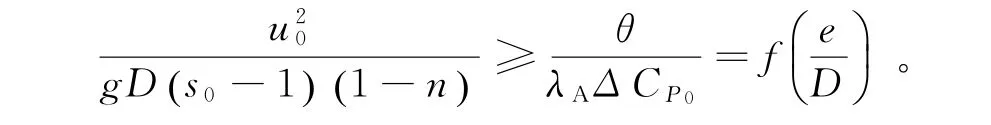
在波浪作用下,管道冲刷暴发与Keulegan-Carpenter数有关,也与管道的埋设深度有关,冲刷暴发条件为

式(4)中,um为床面波浪质点轨迹的最大运动速度;KC为Keulegan-Carpenter数,KC=umT/D,T为波浪周期。

2 控制方程

假定波浪传播方向垂直于管道路由。波浪运动是无旋的,存在流速势函数,其控制方程为Laplace方程

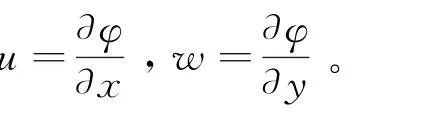
对于微幅波,波浪势为

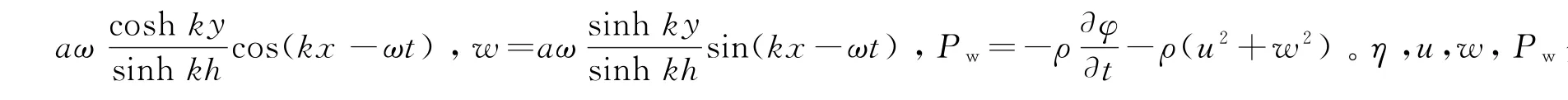
假定渗流符合Darcy定律,渗流控制方程为

式中,P(x,y)为压强。在平坦海床上,波浪动水压强为

显然,式(8)是式(7)的一个边界。根据边界条件的形式,将方程(7)的解表示为P=f(y)cos(kx-ωt),代入到式(7)中,并进一步处理,得到形式如下的解P=c1exp( ky)cos( kx-ωt)+c2exp(-ky)cos(kx-ωt),当沙层无限厚时,解为

如果在y=-d,存在不渗水层,即∂P/∂y=0,则解为

3 边界元法

本文计算区域如图2所示。波浪计算的边界为Γ1,Γ2,Γ3,Γ4。Γ1由海底与未埋藏的管壁构成。在波浪计算中,假定管道不影响较远水体中的质点运动规律,边界条件取为

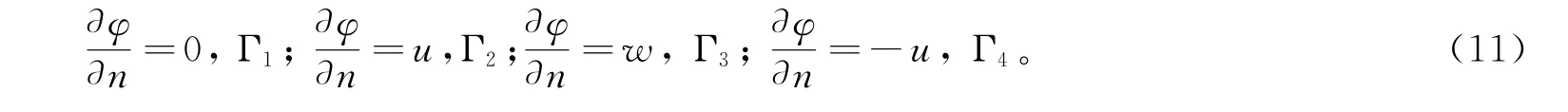
在上式中,n表示边界的外法线方向。上述边界条件全为Neumann型,对于Laplace方程而言,是没有唯一解的,因此,在波浪的入射断面上,改为根据式(6)给定势函数值。

图2 波浪、渗流计算区域示意图Fig.2 A sketch of the computation domain for the sea wave and the seepage flow

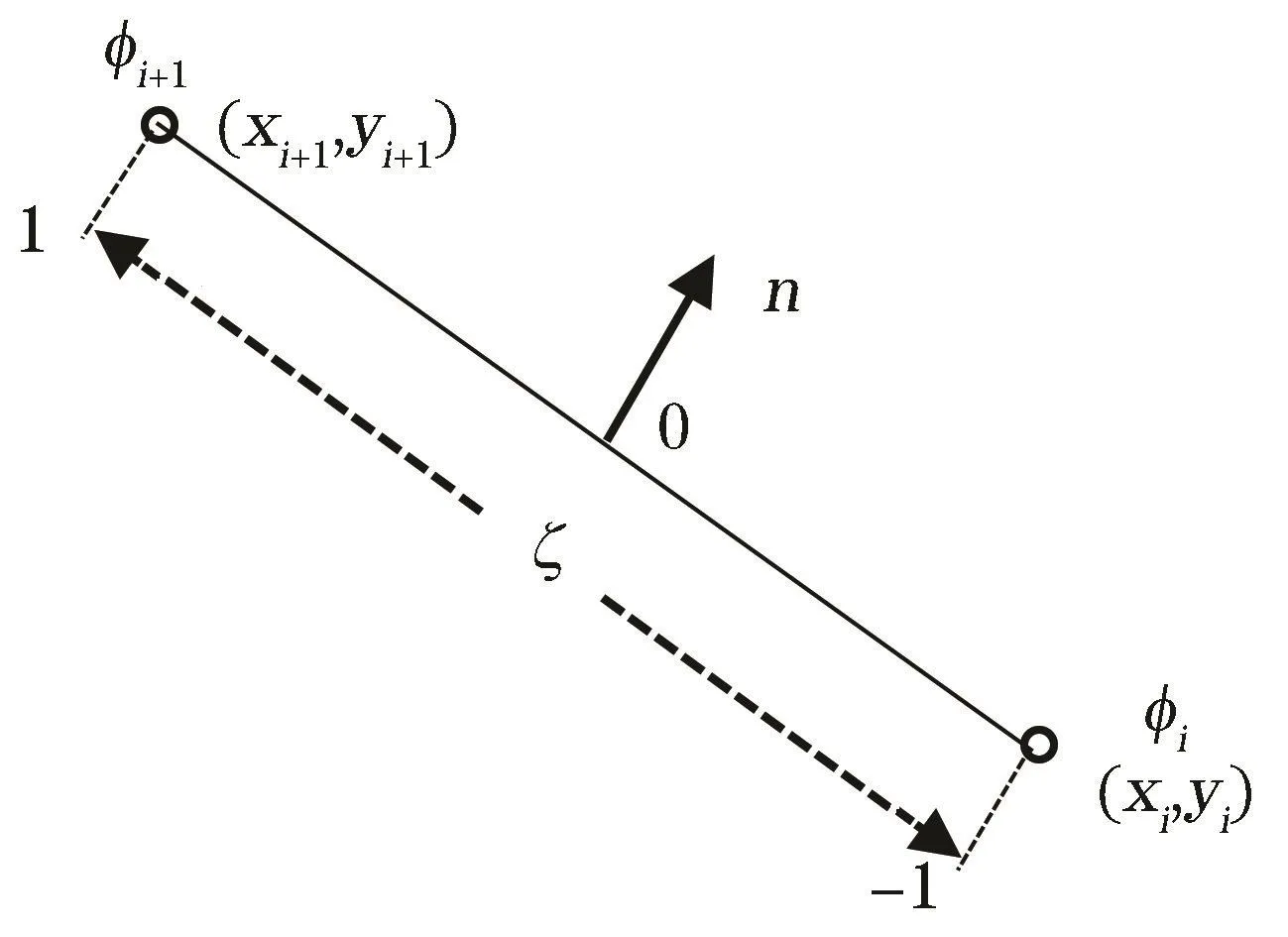
图3 边界积分单元定义Fig.3 Definition of a boundary integral element

24定∂P/∂n,在边界L1上,如果沙层足够厚,则根据式(9)给定压强,如果存在不渗水层,则取∂P/∂n=0。对于Laplace方程,其基础解为

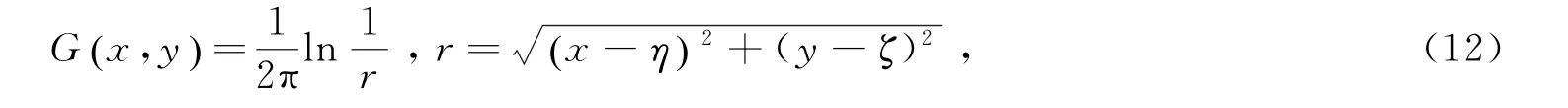
式(12)中,(x,y)与(η,ζ)为计算域中的点,r为点(x,y)到点(η,ζ)的距离。通过格林积分公式

得到Laplace方程的解

式(13)中,Ω为计算域;Γ=Γ1+Γ2+Γ3+Γ4,为计算域的边界;公式左边为计算域中的面积分,右边为边界上的线积分。式(14)中,C为积分系数,C=θ/2π,θ为点(η,ζ)邻域的积分幅度,如(η,ζ)∈ΩΓ,θ= 2π,(η,ζ)∈Γ且光滑,θ=π。

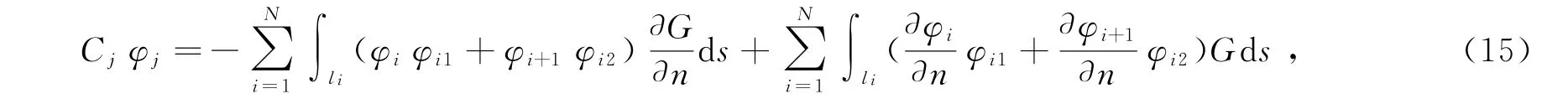
根据式(16),如已知边界上的qi(或φi),就可以确定边界上φi(或qi),边界上φi与qi都已知时,则采用(14)计算区域内任意点的势函数。

对于边界元方法而言,计算区域的边界能被准确拟合,不存在差分法中对奇点难于处理的问题。在管壁与海床接触的位置(图1中的A,B点)处,以A点为例,与其相接的2个边界元记为li-1与li(图4),那么在A点处,有2个外法线方向的压强梯度,其中垂直于管壁的压强梯度∂Pi,2/∂n=0,而A点处的压强Pi也已经通过波浪计算得到,因此,只须要计算垂直于床面的压强梯度∂Pi,1/∂n,而∂Pi,1/∂n则用于判别管道冲刷暴发的临界条件。

数值试验的结果表明,在管壁与交叉点邻近床面,流速与压强变化剧烈,需要较高的空间分辨率,本文计算中,在管壁及与交叉点相距0.5D的床面上,边界元长度取l=πD/72。

计算过程中,将一个波浪周期分为N个时间步长,Δt=T/N,在t=i(-1)Δt,i=1,2,…,N+1时计算波浪,t=i(-1/2)Δt, i=1,2,…,N时计算渗流。设Γ4为波浪入射边界。计算流程如下:

1)采用边界Γ4以式(6)给定波浪势函数,在Γ1,Γ2,Γ3按式(11)给定波浪势函数法向梯度(流速);

2)用边界元法计算t=iΔt,(i+1)Δt时刻的波浪势函数方程(5),得到海底(边界Γ1)的势函数φi,φi+1;

图4 管道与海床交叉处边界元的处理Fig.4 Treatment of the boundary elements at the cross points of the pipeline and the seabed

3)取Pi+1/2w=-ρ(φi+1-φi)/Δt,计算t=(i+1/2)Δt时刻海底的波浪压强,并作为渗流的边界条件,在边界L2,L4上,根据式(9)或(10)给定∂P/∂n,在边界L1上,如透水,则据式(9)给定压强,如果不渗水,则取∂P/∂n=0;

4)用边界元法计算t=(i+1/2)Δt时刻的渗流控制方程(7),得到海底(边界L3)的法向压力梯度∂Pi+1/2/∂n。

上述计算过程中,管道与海底交叉点处的法向压力梯度∂P/∂n大于泥沙水下重量时,管道冲刷暴发。

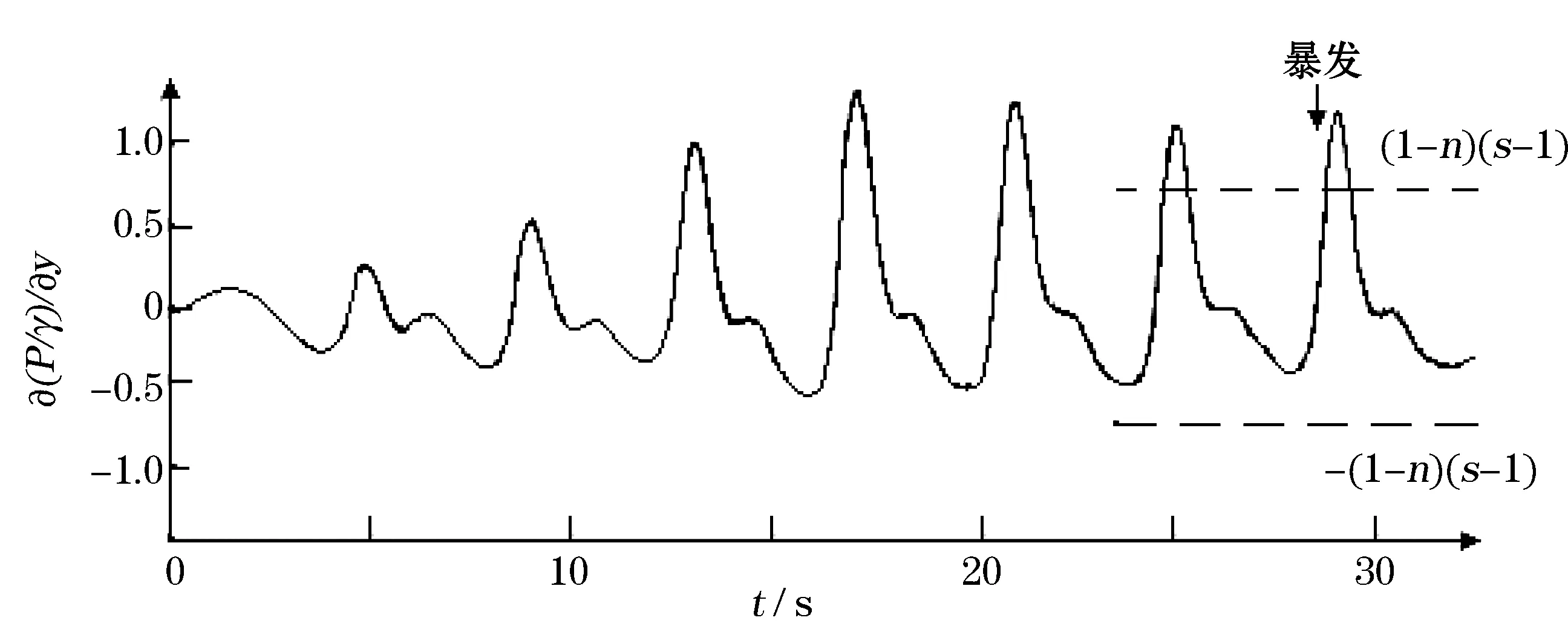
图5 Test O16中交叉点压强梯度过程线[11]Fig.5 Time series of pressure gradient at the cross point in Test O16[11]

4 模型验证

本文采用Sumer等[11]的试验数据进行模型检验。其试验水槽长26.5 m,宽0.6 m,试验水深0.33 m,水槽中部有一段0.10 m厚,3 m长的沙层,泥沙粒径0.18 mm,空隙率0.53。试验条件下,冲刷暴发的临界条件为-∂(P/γ)/∂y≥0.77(γ=ρg,g为重力加速度)。Sumer等的试验中,逐渐增大波高,直到冲刷暴发为止,Test O16给出了交叉点的压强梯度过程(图5)。Test O16的管径为10 cm,埋深0.064倍管径,波浪周期为4 s,波高0.17 m。Test O16条件下,本文计算的交叉点A处的垂向压强梯度如图6所示。计算的最大水头梯度为1.29,与试验的最大值相当。但是,模拟的压强梯度变化过程是对称的,而试验结果是不对称的,计算的最小梯度与试验结果相差较大。其原因在于试验的水深较小,波高较大,管道影响了的波浪的形状,造成了波浪的不对称性,因此,试验中的压强梯度变化是不对称的,而模型不能重现试验中的不对称过程。对于水深较大的情形,管道不影响波浪的对称性,模拟的结果将更真实。Test O17条件下,模拟的速度与压强水头分布如图7,交叉点压强梯度过程见图6。模拟的最大压强梯度为0.83,略大于起动临界条件。在波峰时刻,管道附近水体水平流动,水体与沙体中的压强大致对称分布,交叉点的压强梯度最小。在T/ 4时刻,管道上方水体向下流,埋藏管道下方压强变化剧烈,交叉点的压强梯度最大。在波谷与3T/4时刻,速度与压强分布与波峰与T/4时刻正好相反。试验结果中,交叉点垂向压强梯度达到,甚至大于临界值时,冲刷才暴发。Sumer等[11]对此给出了解释,波浪过程中,交叉点泥沙暴露在临界压强梯度力的时间较短,而冲刷暴发需要一个过程。因此,不同于单向流作用下的冲刷暴发,波浪作用下,垂向压强梯度需要大于临界值。模拟结果,交叉点的压强梯度都略大于或显著大于(如Test O16)临界值。

图6 模拟交叉点A处压强梯度过程Fig.6 Simulation of the time series of pressure gradient at cross point A

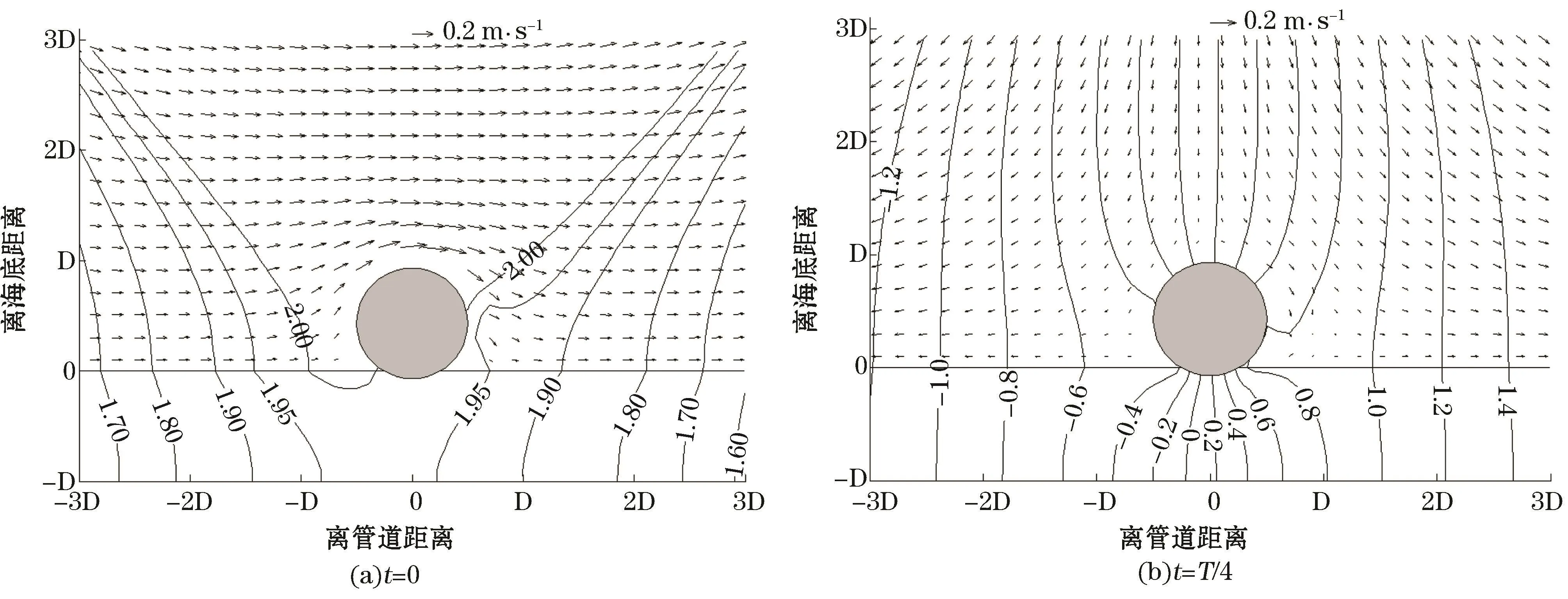
图7 波浪质点速度与压强水头分布Fig.7 Distributions of the wave particle velocity and the pressure head

5 结 语

边界元方法能准确地拟合海底与管壁边界,可以处理管道与海床交叉点数值奇点问题,准确地计算波浪与渗流。本文采用边界元方法计算了波浪作用下管道冲刷暴发临界条件,计算结果与试验结果符合良好。模型方法程序设计简单,计算精度高,可根据波浪与管道埋深条件,快速计算交叉点的垂向压力梯度,判断管道是否会发生冲刷,弥补了根据试验图示判别的不足。

当然,本文方法也有适用范围。1)本文方法是采用线性波理论计算水体中的压力场及线性波作用下的渗流场,而在波浪破碎带内,波面发生了变形,已不能用线性波来描述,本文方法就已经失去了其赖以建立的条件,可能产生较大的误差。对于近岸波浪,非线性波理论更合适,理论上,如果利用非线性波的势函数,建立非线性波作用下的渗流场解析解,文中方法可以推广到非线性波情形。2)渗流计算中,没有考虑海床的变型,这就意谓着模型只能用于沙质海床。

基于Navier-Stokes方程,采用差分法或有限元法计算的波浪冲刷暴发时,都用振荡流代替波浪运动,可能与真实的波浪运动有差异。而边界元方法则可以准确模拟波浪过程。对于波浪作用下的冲刷暴发,边界元方法可能更为简单而准确。当然,边界元方法的局限性也是明显的,对于单向流或波流联合作用下的冲刷暴发,水体运动都不能用势流模型模拟,边界元也就失去了意义。

[1]LI F,CHENG L.Numerical model for local scour under offshore pipelines[J].Journal of Hydraulic Engineering,1999,125(4):400-406.

[2]LI F,CHENG L.Prediction of lee-wake scouring of pipelines in currents[J].Journal of Waterway,Port,Coastal,and Ocean Engineering,2001,127(2):106-112.

[3]BRORS B.Numerical modeling of flow and scour at pipelines[J].Journal of Hydraulic Engineering,1999,125(5):511-523.

[4]SUMER B M,JENSEN H R,FREDSOE J.Effect of lee-wake on scour below pipelines in current[J].Journal of Waterway,Port,Coastal,and Ocean Engineering,1988,114(5):599-614.

[5]YEGANEH-BAKHTIARY A,KAZEMINEZHAD M H,ETEMAD-SHAHIDI A,et al.Euler-Euler two-phase flow simulation of tunnel erosion beneath marine pipelines[J].Applied Ocean Research,2011,33(2):137-146.

[6]DUPUIS A,CHOPARD B.Lattice gas modeling of scour formation under submarine pipelines[J].Journal of Computational Physics, 2002,178(1):161-174.

[7]MAO Y.The interaction between a pipeline and an erodible bed[D].Lyngby,Denmark:Technical University of Denmark,1986.

[8]CHIEW Y M.Mechanics of local scour around submarine pipelines[J].Journal of Hydraulic Engineering,1990,116(4):515-529.

[9]SUMER B M,FREDSOE J.Onset of scour below a pipeline exposed to waves[J].International Journal of Offshore and Polar Engineering,1991,1(3):189-194.

[10]KLOMP W H G,HANSEN E A,CHEN Z,et al.Pipeline seabed interaction,free span development[C].Proceeding 5th International Offshore and Polar Engineering Conference Netherlands:The Hague,1995(II):117-122.

[11]SUMER B M,TRUELSEN C,SICHMANN T,et al.Onset of scour below pipelines and self-burial[J].Coastal Engineering,2001,42 (4):313-335.

[12]YANG B,GAO F P,WU Y X,et al.Numerical study of the occurrence of pipeline spanning under the influence of steady current[J]. Shipbuilding of China,2005,46(Suppl.1):221-226.杨兵,高福平,吴应湘,等.海流引起海底管道悬空的数值模拟[J].中国造船,2005,46 (增刊1):221-226.

[13]LIANG D,CHENG L.A numerical model of onset of scour below offshore pipelines subject to steady currents[J].Frontiers in Offshore Geotechnics,2005:637-644.

[14]ZANG Z,CHENG L,ZHAO M,et al.A numerical model for onset of scour below offshore pipelines[J].Coastal Engineering,2009, 56:458-466.

[15]ANG W T.A Beginner’s course in boundary element methods[M].Boca Raton USA:Universal Publishers,2007:1-34

Boundary Element Method for Calculating the Onset of Scour Beneath Marine Pipelines Under the Wave Action

XIA Hua-yong1,WANG Jun-qin2
(1.South China Sea Marine Forecasting Center,Guangzhou 510300,China; (2.Engineering Design Department,CNOOC Research Institue,Beijing 100027,China)

The critical condition of the onset of scour beneath marine pipelines is one of the important fundamental parameters for the design and operation of submarine pipelines.Sumer et al gave the test curves of pipeline scour onset under the wave action,which included only three curves of Keulegan-Carpenter (KC)number.For an arbitrary KC number,however,the Sumer et al's method is not convenient for use and also not accurate.It is,therefore,necessary to establish a numerical model for calculating the critical condition of the onset of pipeline scour under the wave action.Because the intersection of the pipelines with the seabed can form a complex geometrical shape and the cross points are numerical singularity,the calculation of the critical condition of the onset of pipeline scour becomes very difficult.For this reason,the Boundary Element Method(BEM)is applied to calculate the wave motion and the seepage pressure.The boundary elements can precisely fit the boundary between the seabed and the pipeline wall,easily solve the problem about the numerical singularity at the cross points of the pipeline and the seabed and directly calculate the vertical pressure gradient at the cross points.Thus,the critical condition of the onset of pipeline scour can be accurately calculated.The calculated results agree well with the experiments available in literatures.

marine pipeline;onset of scour;boundary element method;numerical singularity

September 13,2016

P75

A

1002-3682(2017)02-0009-08

10.3969/j.issn.1002-3682.2017.02.002

2016-09-13

水利工程仿真与安全国家重点实验室开放基金资助项目——沙脊沙波及路由海床稳定性研究(HESS1401)

夏华永(1967-),男,湖南沅江人,研究员,博士,主要从事海洋动力学调查方面研究.E-mail:xiahuayong2001@21cn.com