改进的洛仑兹曲线模型
2017-07-07庄小红盛世明
庄小红,盛世明
(上饶师范学院 经济与管理学院,江西 上饶 334001)
改进的洛仑兹曲线模型
庄小红,盛世明
(上饶师范学院 经济与管理学院,江西 上饶 334001)
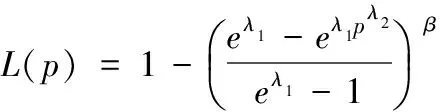
洛仑兹曲线方程;收入分配;数值拟合
1 洛仑兹曲线的描述
1905年,美国统计学家M.O.洛仑兹按收入从低到高对全国人口进行排序,并依次计算出占该序列人口向上累计百分比对应的收入百分比。例如,某国家按收入从低到高排序后20%人口,40%人口,60%人口……对应的收入百分比分别是0.5%,6%,20%……,并将二者的对应关系绘制到图形上,所得曲线即为洛仑兹曲线[1]。将按收入从低到高排序后的人口向上累计频率绘制成横轴OH,对应的收入累计频率绘制成纵轴OM,绘制后图形一般为一条下凸曲线,如图1中曲线a、b所示。观察两条曲线,我们发现二者的弯曲程度明显不一样——b曲线较a曲线而言更弯曲,具体可描述为:对于同一人口累计频率,a曲线上对应的收入百分比大于该人口累计频率在b曲线上对应的收入百分比,即a曲线较b曲线具有更均等的收入分配。由此我们可知,弯曲程度越大的洛仑兹曲线,其所表示的收入分配情况越不均等。图示上还有两条更为极端的曲线:OL直线和OHL折线。直线OL表示收入分配完全均等,国民享有完全一样的收入;折线OHL表示收入分配完全不平等,资本完全集中在一人手中。
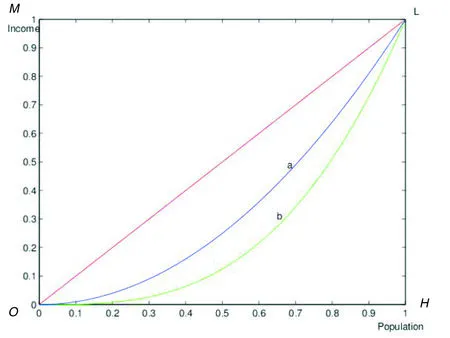
图1 洛仑兹曲线图
2 洛仑兹曲线方程
设经济系统中的人口按收入从高到低进行了排序,记p∈[0,1]是低收入端的累计人口比例,记
L(p)∈[0.1]为该人口拥有的总收入比例,称由此定义的函数:
L(p):[0,1]→[0,1]
为洛仑兹曲线[2]。
记函数f(x)为收入分配的密度函数,其中x>0表示正收入。由收入分配经验分析可知,收入分配曲线一般是正偏的,即峰值点向左偏,右端拖一个长尾巴。记收入分配密度函数f(x)对应的分布函数为F(x),则有p=F(x),其表示收入不超过x的人口比例。由定义可知,设u为平均收入,L(p)表示收入不高于x的人口所拥有的收入比例,则

由上论述,我们可以得到,从收入分配的统计分布出发可以得到相应的洛仑兹曲线,反之,若洛仑兹曲线已知且二次可微,则可以得到其对应的收入分配统计分布。由此我们可以得到曲线L(p)是洛仑兹曲线的充分必要条件为:
L(0)=0,L(1)=1,L'(p)≥0,L''(p)≥0
即洛仑兹曲线L(p)在单位正方形内为凸增曲线。
利用洛仑兹曲线可以对收入分配的均等程度进行直观的分析,即洛仑兹曲线的位置越高,其对应的收入分配越平等。在洛仑兹曲线的基础上,意大利统计学家基尼1912年提出基尼系数,该系数是用于判断收入分配的差异状况,用符号G表示,其定义为:
到目前为止,主要通过三种方法来确定洛仑兹曲线方程:几何计算法,间接拟合法和曲线拟合法。实际上,不论利用哪种方法去计算洛仑兹曲线都是不易的。几何计算法是根据数据资料所显示的特征去选择适当的几何图形(主要是矩阵)去近似逼近计算p在各个点处L(p)的值,因此它无法获取洛仑兹曲线方程。但可以利用几何计算法计算求解基尼系数,但由于逼近过程中图形的割舍会导致所计算出的基尼系数比实际数值要小,这一情况在数据量较少的时候尤为明显。间接拟合法是利用数据资料首先拟合求解出收入分配的密度函数,再根据洛仑兹曲线方程L(p)的计算方程式求解出来。这一方法在理论上是成立的,但由于密度函数计算的复杂性而在实际操作中很少用到。间接拟合法是根据数据资料所描绘的图像特征选择适当的函数曲线(如二次函数,指数函数,幂函数等)去直接拟合洛仑兹曲线。由于该方法在实际操作中简便易行,所以被广泛使用,但在计算过程中要考虑拟合精度的要求。
查阅相关文献可以知道利用第三种方法,学者们已获取得到基本的洛仑兹曲线模型有[2-5]:
L1(p)=p;
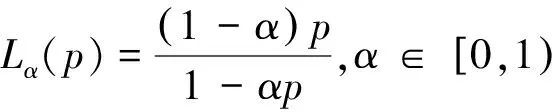

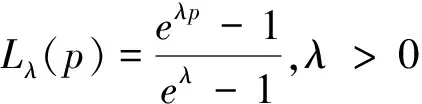
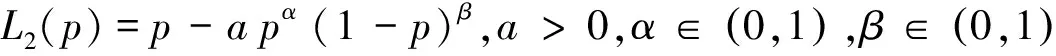
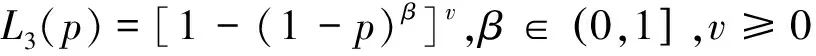
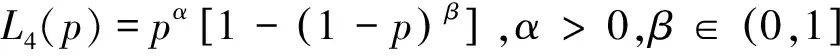
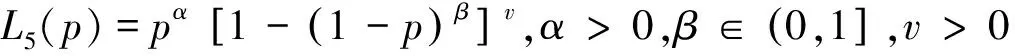
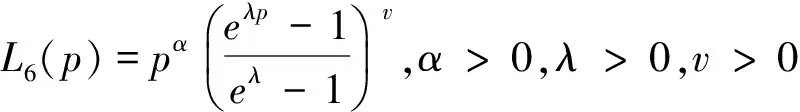
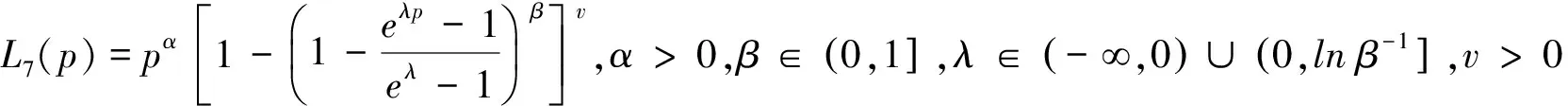
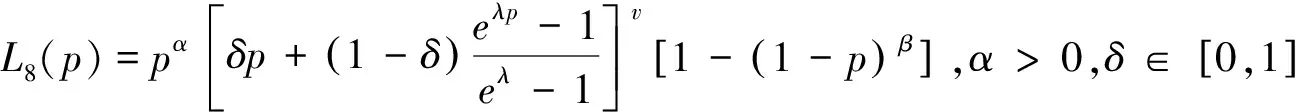
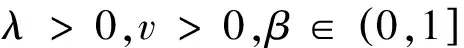
3 改进的洛仑兹曲线模型
在构造新的洛仑兹曲线之前,我们先来看洛仑兹曲线满足的基本性质。
定理3.1 构造如下函数:
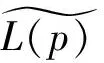
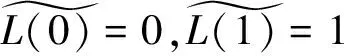
且因为L(p)满足L'(p)≥0,则
又L''(p)≥0且β∈(0,1],则β-1≤0,故有
综上,定理得证。
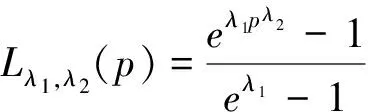
下面定理3.2将证明该模型Lλ1,λ2(p)满足洛仑兹曲线的条件。
定理3.2 函数模型Lλ1,λ2(p)为洛仑兹曲线当且仅当λ1>0,λ2>0且λ2+λ1λ2pλ2-1≥0。
证明:模型Lλ1,λ2(p)为洛仑兹曲线的充分必要条件为:
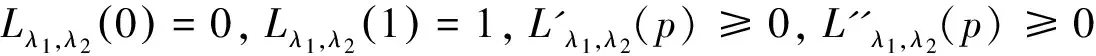
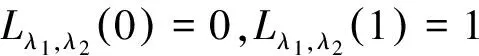
其次,对模型Lλ1,λ2(p)求解一阶偏导数为:
则要使曲线Lλ1,λ2(p)的一阶及二阶偏导数均大于或等于零的充分必要条件是:
λ1>0,λ2>0且λ2+λ1λ2pλ2-1≥0
定理得证。
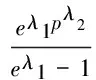
注记3.1 当λ2=1时,Lλ1,λ2(p)退化为曲线Lλ(p)。
注记3.2 当λ1→0,λ2=1时,Lλ1,λ2(p)→L1(p)=p。
定理3.3 结合定理3.1和定理3.2,我们易得到如下函数也满足洛仑兹条件:
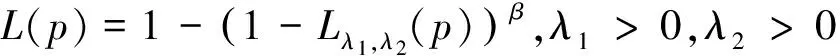
即曲线L(p)为洛仑兹曲线。
4 数值模拟
在上一节中我们确定了本文所要研究的洛仑兹曲线L(p),下面我们将通过对比该洛仑兹曲线与原有10种洛仑兹曲线的均方误差、平均绝对误差以及最大绝对误差等来分析该洛仑兹曲线的准确性和科学性。下面我们先给出均方误差、平均绝对误差、最大绝对误差的公式,并称其为判定洛仑兹曲线拟合精度的“三个标准”。
(1)均方误差(MSE,mean squared error):
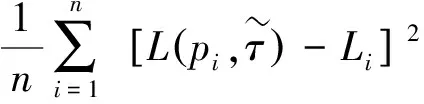
(2)平均绝对误差(MAE,mean absolute error):
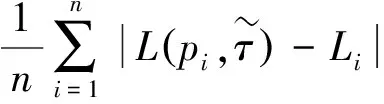
(3)最大绝对误差(MAS,maximum absolute error):
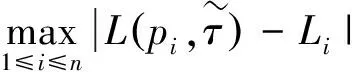
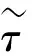
对新构造的洛仑兹曲线L(p)以及第2部分所提及的洛仑兹曲线,对表1数据采用最小二乘法对曲线中的参数进行估计,并分别对所有曲线的拟合效果进行分析,将所得结果列于表2。
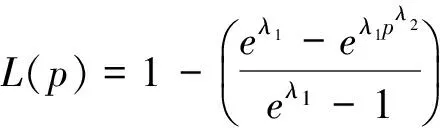
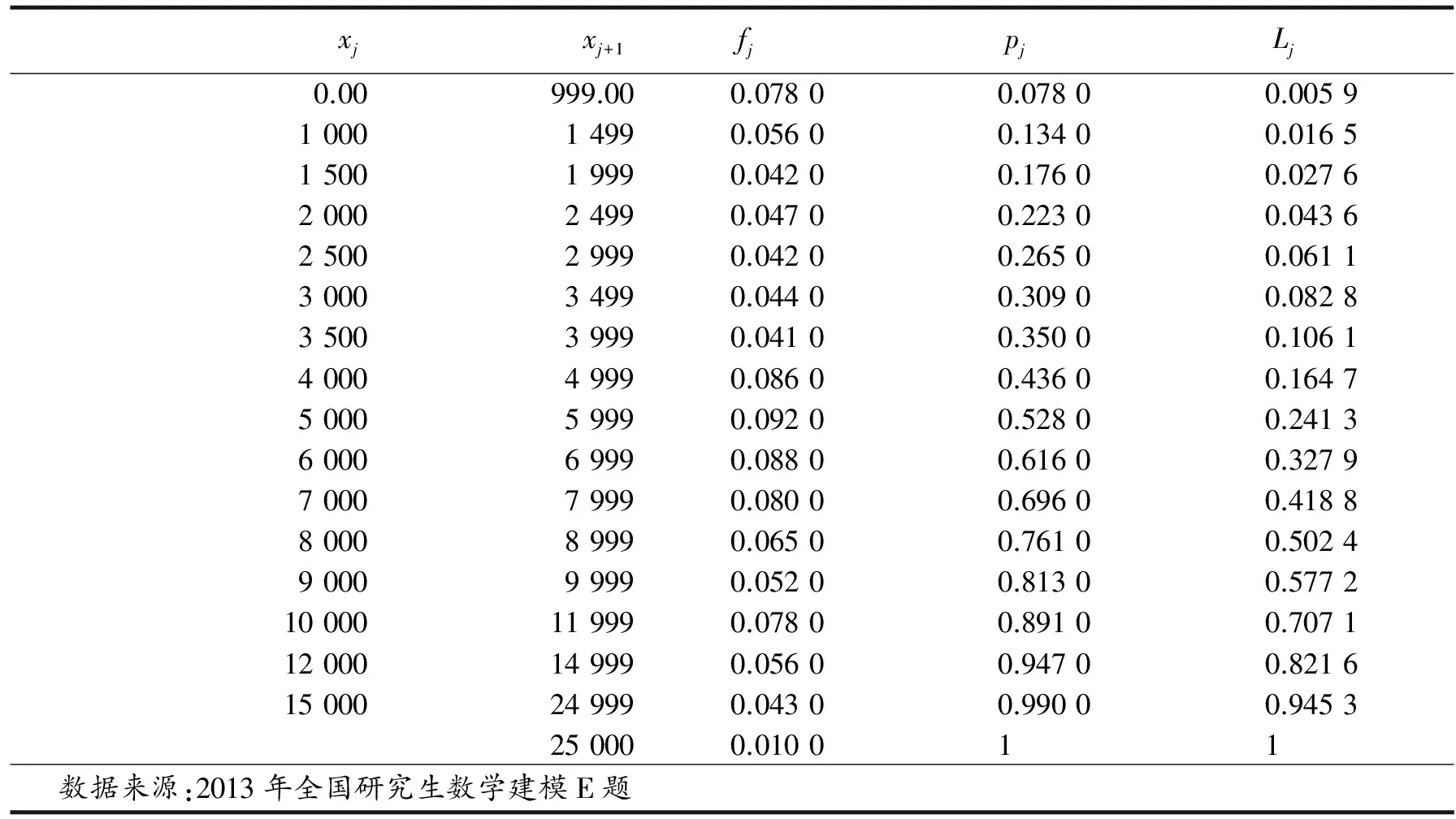
表1 收入分配分组数据
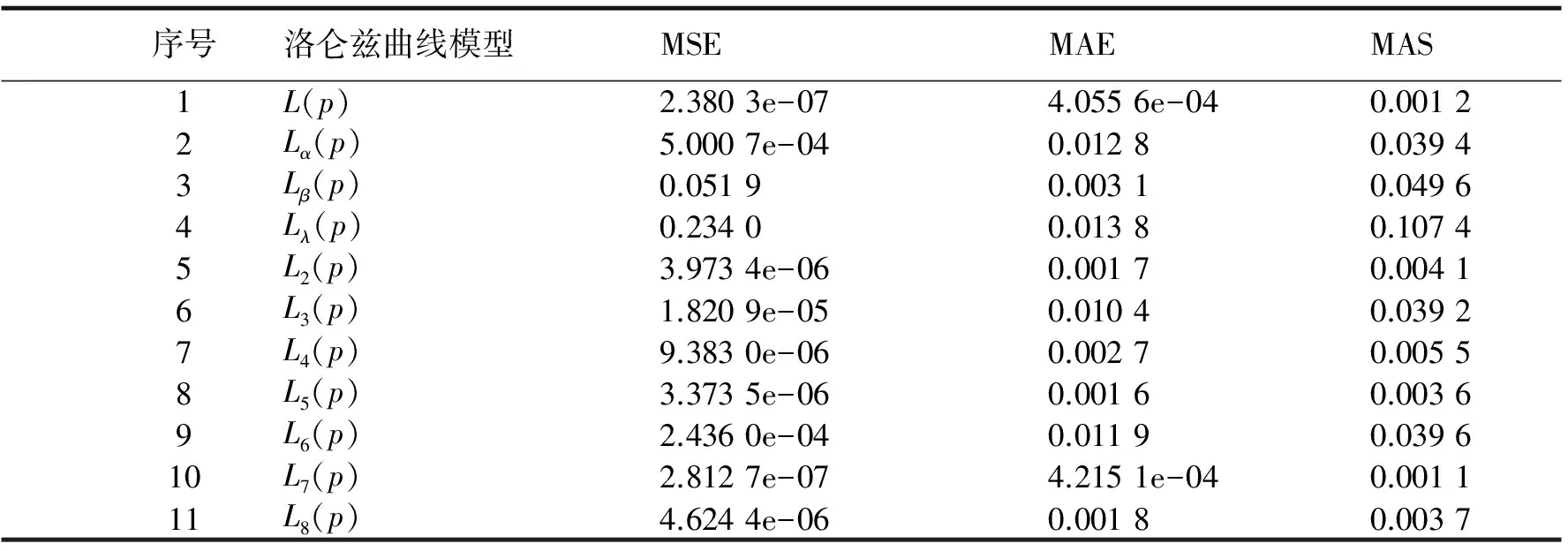
表2 洛仑兹曲线拟合精度的“三标准”
[1] 张奎,王原君,SARABIA J.洛仑兹曲线模型的推广[J].应用数学,2010,23(3):501-507.
[2] FOSTER J,WOLFSON M.Polarization and the decline of the middle class[J].Canada and the U S Journal of Economic Inequality,2009,8(2):247-273.
[3] WANG Z X,SMYTH R.A hybrid method for creating Lorenz curves with an application to measuring world income inequality[J].Business and Economics,2013,46(13):4-21.
[4] WANG Z X,SMYTH R.A general method for creating Lorenz curves[J].The Review of Income and Wealth,2011,57(3):561-582.
[5] BLACKBURN M L,BLOOM D E.What is happening to the middle class?[J].American Demographics,1969,7(1):19-25.
The Improvement Model of Lorenz Curve
ZHUANG Xiaohong, SHENG Shiming
(School of Economics and Business Management,Shangrao Normal University, Shangrao Jiangxi 334001, China)
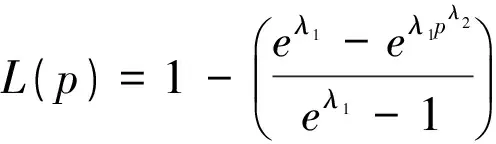
Lorenz curve equation; income distribution; numerical simulation
2016-11-16
上饶师范学院青年科研基金项目(2014-11-14)
庄小红(1987-),女,福建泉州人,助教,硕士,主要从事统计学研究。E-mail:304623577@qq.com
TU352.11
A
1004-2237(2017)03-0039-05
10.3969/j.issn.1004-2237.2017.03.008
