基于双边滤波的各向异性扩散方程图像去噪
2017-07-07许冠军喻晓
许冠军,喻晓
(1.台州科技职业学院 信息学院,浙江 台州 318020;2.上饶师范学院 数学与计算机科学学院,江西 上饶 334001)
基于双边滤波的各向异性扩散方程图像去噪
许冠军1,喻晓2
(1.台州科技职业学院 信息学院,浙江 台州 318020;2.上饶师范学院 数学与计算机科学学院,江西 上饶 334001)
近年来,各向异性扩散方程模型在图像去噪和特征提取中得到广泛应用。双边滤波为非迭代图像去噪算法,此方法因简单而高效而备受关注。在对两种模型优缺点分析的基础上,结合双边滤波的非线性特点,用双边滤波预光滑,在各向异性扩散方程中使用预光滑图像进行边界检测。和Alvarez等使用高斯核卷积提取边界相比,双边滤波体现了预处理的各向异性,提高了边界检测的准确性。改进的扩散方程的强迫项,在保证去噪效果的同时,提高了迭代的收敛速度。
双边滤波;各向异性扩散方程;扩散系数;边界检测;图像去噪
在图像处理和分析领域,图像去噪是该领域的研究热点,可以参见文献[1-7]等。图像去噪有两个目标:(1)去除噪声;(2)保持图像边界特征。噪声是图像的高频部分,而图像的边界和特征也是图像的高频信息。因此,在去噪同时,也使得图像的边界特征变得模糊。去噪模型的好坏,很大程度上由能否解决好两个目标之间的矛盾决定。
在图像去噪领域,双边滤波模型(以下简称BF模型)和各向异性扩散模型(以下简称为AD模型)是被广泛讨论的两类算法。BF模型是对高斯滤波的改进,在权函数中同时考虑空间距离和像素值差距两个权因子,为局部非线性滤波算法。由Perona-Malik[1]提出的各向异性扩散模型(以下简称P-M模型),推动了PDE方法在数字图像处理领域的广泛应用。该模型得到了众多学者的关注,并涌现出大量研究成果[2-9],使得该模型的数学理论和数值算法得到了完善。AD模型中的各向异性是建立在对图像边界的准确判断之上,而P-M模型以及Catt等[3]和Alvarez等[4]的改进模型对边界的确定,是使用像素灰度值或是像素灰度值卷积后的梯度模来判定。在文献[1]指出,卷积运算在方程模型上表现为各向同性扩散方程。Catt等的模型是建立在各向同性判断边界的基础上,进行各向异性扩散,这样处理使模型的整体各向异性的性质没有得到充分体现。
本文对AD模型和BF模型的各自特性分析的基础上,应用BF代替高斯滤波预处理图像,并用预处理图像的梯度模进行边界强度估计。为了使模型具有较好的收敛性又保证良好的去噪效果,本文改进了扩散方程的强迫项。
1 相关工作
1.1 各向异性扩散模型(AD)
Pietro和Malik[1]提出基于各向异性扩散方程的图像光滑模型,克服了低通滤波图像平滑中各向同性的缺点,使得图像在每个像素点根据灰度分布,有选择地进行各向异性扩散。P-M模型实质上用梯度模‖u‖来检测边界,在边界处有较小的扩散系数,平滑较少,在非边界处则平滑较多。模型在抑制噪声的同时,很大程度上保持了图像的边界。
P-M模型的不适定性,在强噪声图像中,直接计算图像梯度,将不足以区分噪声和边界,因此很难用梯度模来估计边界。Catt等[3]提出了改进模型(以下简称Catt模型),用适度平滑图像的卷积梯度模‖(Gσ*u)‖来代替‖u‖进行边界检测。其模型表达式如下:
(1)

Alvarez等[4]又提出了基于平均曲率运动方程的去噪模型(Alvarez模型),并证明了其适定性。其表达式为:
(2)
取h(·)为非减函数,满足0≤h(·)≤1,h(·)的变化趋势和g(·)相异。在图像的平滑区域,该模型以各向同性扩散为主;而在图像的边界和特征区域,沿垂直法向方向扩散为主。图像整体区域的扩散系数依赖于g(·)。
1.2 双边滤波模型(BF)
双边滤波[5-6]模型简洁,且为非迭代、局部去噪算法,易于程序实现。在低噪图像的处理中能达到较好的去噪效果,也容易推广到RGB彩色图像的处理。其表达式如下:
BF(u)(x)=∫ΩWD(x,y)WR(x,y)u(y)dy.
(3)
其中WD(x,y)是衡量像素x和y在几何上邻近程度的函数,WR(x,y)是衡量像素之间灰度值的相近程度。该模型同时体现几何邻近程度和像素灰度值相似程度,因而称之为双边滤波。
BF模型去噪的基本原理是根据邻域内像素灰度值的分布情况,生成权重分布函数,具有各向异性的基本特征。在图像边界处,仅依赖距离的邻域卷积运算会导致图像边界变得模糊。增加了灰度值权因子后,图像在边界处灰度值跳跃较大,因而其权值较小(图1),从而有效保持边界信息。

(a)噪声图 (b)权函数分布 (c)去噪结果
2 基于双边滤波的各向异性扩散模型
2.1 AD模型和BF模型的分析比较
BF模型最大的优点是其非迭代性,计算量小,而且很容易并行计算。数值实验表明,根据图像特征选择适当的σD和σR,一步计算就能起到很好的去噪效果。而在图像的平滑部分,由于模型的局部性,使得去噪结果有明显的噪声斑块。若要得到更好的去噪效果,需要自适应地计算相应的σD(t)和σR(t)。构造恰当的σD(t)和σR(t)函数相对复杂,而多步计算,又会使得图像过度平滑。
数值实验还表明该模型对于灰度尺度σR的选择非常敏感。当σR值较小时,去噪结果图像中会出现许多明显的奇点;而σR值较大时,其去噪效果和高斯滤波类似,会使图像过度平滑。由于模型的局部性,即使选择比较合适的σD和σR,也不能解决噪声斑块问题。
AD模型的扩散系数由图像所在的区域决定,在图像平滑区域扩散系数大,对图像平滑较多;而在边界区域扩散系统小,平滑也较少。AD模型在图像尺度空间上平缓去噪,对平滑区域的去噪能力较强。模型的去噪能力依赖于对图像边界的准确判断。模型具有保持边界的特性,若对图像进行长时间的扩散处理,最终处理结果将是初始图像灰度平均值的单色图像。因此,图像在扩撒去噪的同时,也模糊了边界。如何选择合适的扩散截至时间也是AD模型的一个讨论方向,文献[8]以及[10]对此做了专门分析。
为提高迭代的收敛速度,在模型方程右侧增加强迫项f(u-u0),通常取f(u-u0)=λ(u-u0)。强迫项的目的是保持去噪图像和原始图像的相似性,若原图噪声较强,则处理结果也保持了大量噪声。
2.2 基于双边滤波的各向异性扩散模型

(a)高斯卷

(b)双边滤波
为了加快模型的收敛速度和保持图像特征,引入强迫项。在其他模型中,强迫项对整体图像作同等处理,该方法在保持图像边界特征的同时,也保留了噪声成分。改进模型中,只对图像的边界,即图像的特征处使用强迫项,其表达式如下:
f(u-u0)=h(‖‖)(u0-u).
(4)
h(·)的函数表达式如(2)式。改进的强迫项,在保证收敛性的同时,也保持了图像的特征区域,而在平滑区域,强迫项几乎不起作用,能较好地抑制平滑区域的噪声,下面给出本文模型的表达式:
(5)
其中v(·)为平均曲率运动方程去噪表达式。
2.3 数值求解
本文采用有限差分法求解方程(5)的数值解[12-13],下面给出求解过程中的几个常用表达式:
则div=cos2θuyy-2sinθcosθuxy+sin2θuxx。一阶偏导数采用9点格式,其差分格式为:


则Δu的差分格式为:

混合二阶偏导数uxy采用4点差分格式:
算法步骤如下:
1)用BF模型预光滑原始噪声图像u0,得:
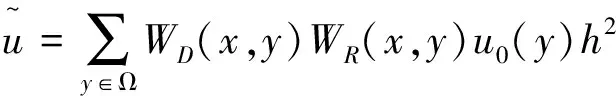
(6)

3)模型求解的半隐格式方程如下:
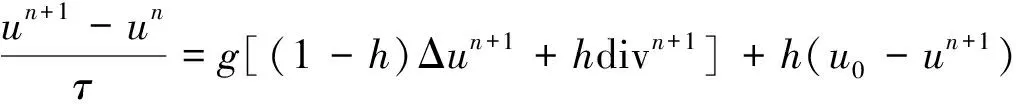
(7)
差分方程中的九点,生成的9对角线性方程:
A(un)un+1=τhu0+un.
(8)
4)用Jocobi迭代求解方程(8),令A(un)=L+D+U.其中D为对角阵,L为下对角阵,U为上对角阵,迭代格式为:
xm+1=-D-1(L+U)xm+D-1(τhu0+un).
(9)
Jocobi迭代结果xM作为方程(8)的解un+1=xM。注:在计算中取时间步长τ=1,空间步长h=1。
3 实验结果与分析
实验中使用Lena(256×256),Cameramen(256×256)两幅图(图3~4)像对所提算法进行验证。两个数值实验均在原图中加入均值为0,方差σ2=0.003的高斯白噪声。其实验参数如表1,去噪结果比较如表2。为了简化计算,式(5)中Ω区域取5×5的小窗口。

表1 数值实验参数
本文使用平均平方误差(MSE)来反映去噪图像和原图像的逼近程度,在实验中用无噪声图像和去噪结果之间的MSE来衡量去噪模型的去噪效果。

(10)
其中u(·)为无噪声图像,D(u)(·)为去噪结果图像。

表2 去噪结果比较(MSE)
人的视觉对于图像不同部分的灰度偏差存在不同的敏感度,MSE是对所有像素做同等加权,所以其大小并不直接决定图像的去噪效果。但在一般意义上,MSE越小去噪效果越好。
由表1可以看出,本文的方法在两个实验中迭代十多次就达到了最佳的MSE,具有较快的收敛速度,且去噪后图像的边界较AD模型更清晰;和BF模型相比,本文的算法在平滑区域基本上消除了噪声痕迹。从表2中MSE数据也可以看出,本文的方法在给定的噪声环境下,具有更好的去噪效果。

图3 Lena去噪

图4 Cameramen去噪
4 结束语
BF模型是比较有效的去噪方法,该算法的局部性,使得去噪结果有噪声斑块。尽管BF模型去噪具有较小的MSE,但去噪图像的整体视觉效果不够理想。AD模型具有各向异性的特点,但随着扩散的持续进行,会引起图像细节的模糊。若要达到消除噪声痕迹,并保持图像细节,扩散系数的准确性至关重要,这对边界提取提出了很高的要求。
本文用BF模型预处理图像进行边界检测,数值实验显示和使用高斯核卷积相比,边界判断更为准确。这使得扩散模型中的扩散系数更加准确,提高了AD模型的整体去噪能力。本文还改进了AD模型中的强迫项,使强迫项仅对图像的特征部分起作用。改进后的模型,有较快的收敛速度,去噪效果也优于AD模型和BF模型。但对于强纹理图像和强噪声图像,由于梯度判断边界本身的准确性问题,处理效果不够理想,更优的边界或纹理判断因子也是今后的研究方向。
[1] PERONA P,MALIK J.Space and edge detection using anisotropic diffusion[J].IEEE Trans Pattern Anal Machine Intell,1992,12(4):629-639.
[2] KICHENASSAMY S.The Perona-Malik paradox[R].Minnesota:Department of Mathematics,Tech Rep Univ,1996:3-12.
[3] CATT F,Lions P L,Morel J M.Image selective smoothing and edge detection by nonlinear diffusion[J].SIAM J Numer Anal,1992,29(2):182-193.
[4] AlVAREZ L,LIONS P,JEAN-MICHELl M.Image selective smoothing and edge detection by nonlinear diffusion II[J].SIAM J Numer Anal,1992,29(4):845-866.
[5] TOMASI C,MANDUCHI B.Filtering for gray and color images[C].New Delhi:6th Int Conf Computer Vision,1998:839-846.
[6] MICHAEL E.On the origin of the bilateral filter and ways to improve it[J].IEEE Trans Image Processing,1998,11(2):1141-1151.
[7] 许冠军. 数字图像去噪算法研究[D].杭州:浙江大学数学科学研究中心,2006:27-32.
[8] MRAZEK P.Selection of optimal stopping time for nonlinear diffusion filtering[R].Vancouver:Scale-Space and Morphology in Computer Vision,Third International Conference,2001:290-298.
[9] 张元林,郑南宁,袁泽剑.一种改进的图像自适应非线性滤波方法[J].西安交通大学学报,2004,38(1):162-166.
[10] 谢美华,王正明.基于最小相关系数的扩散去噪的最优停止时间选取[J].计算机应用,2005,25(2):1078-1080.
[11] ROUSSEEUW P,LEROY R,ROBUST A.Regression and outlier detection[M].Newk York:Wiley,1987:13-18.
[12] 董婵婵,张权,郝慧艳,等.基于差分曲率的偏微分方程图像降噪算法[J].计算机工程与设计,2015,36(7):1850-1854.
[13] 陈龙,蔡光程.基于PDE的图像去噪方法[J].计算机工程与应用,2015,51(16):142-145.
Anisotropic Diffusion Image Denoising based on Bilateral Filtering
XU Guanjun1, YU Xiao2
(1.College of Information, Taizhou Vocational College of Science & Technology, Zhejiang Taizhou 318020, China; 2.School of Mathematics and Computer Science, Shangrao Normal University, Jiangxi Shangrao 334001, China)
In recent decades,anisotropic diffusion model was widely used in image denoising and edge detection.Bilateral filtering image denoising is highly concerned because of it’s non-iterative,simple and efficient. In this paper both advantages and disadvantages of the two algorithms are studied. Based on the characteristics of bilateral filtering and anisotropic diffusion, using the bilateral filtering to substitute Gaussian convolution in Alvarez model ,which improved edge detection. The forcing term is introduced to ensure the denoising performance, and improves the convergence rate of the iteration.
bilateral filtering;anisotropic diffusion; diffusivity; edge detection; image denoising
2017-01-11
国家自然科学基金(11561057);江西省自然科学基金(20151BAB211002);浙江省教育技术研究规划课题(JA006);江西省教育厅科技项目(GJJ151054)
许冠军(1981-),男,浙江台州人,高级工程师,硕士,主要从事图像处理、云计算等方面研究。E-mail: mathgary@gmail.com
TP391.41
A
1004-2237(2017)03-0011-06
10.3969/j.issn.1004-2237.2017.03.003
