基于STAR-CCM+汽车散热器的换热分析及结构优化
2017-07-07许晓文孙后环华广胜
许晓文, 孙后环, 华广胜
(1. 南京工业大学 机械与动力工程学院,南京 210000;2. 中国合格评定国家认可委员会,北京 100000)
基于STAR-CCM+汽车散热器的换热分析及结构优化
许晓文1, 孙后环1, 华广胜2
(1. 南京工业大学 机械与动力工程学院,南京 210000;2. 中国合格评定国家认可委员会,北京 100000)
以汽车发动机冷却水箱C207散热器为研究对象,基于计算流体力学软件STAR-CCM+对散热器进行流固耦合模态分析,运用线性回归分析方法确定冷却液参数数据的回归模型,并导入自定义场函数中,采用标准K-Epsilon湍流模型分析冷却液在散热器水道内的温度、压力以及速度变化情况.为了提高散热器的换热效率,对散热片结构进行改善和优化,最终得到较好的换热效果.
计算流体力学;线性回归分析;散热器;STAR-CCM+
现代汽车冷却系统的工作方式是通过大量吸收发动机及其零件的热量,来保证机器在合适的环境内进行工作.冷却系统中的散热器负责依靠冷却液进行散热,它的水管和散热片多用铝材制成[1].冷却液在散热器水道内流动时,冷却液因吸收受热板散出的热量而升温,受热板则由于向冷却液散热而降温,因此,散热器属于热交换器中的一种[2].
冷却系统的散热性能对发动机的影响愈来愈显著,因此,需要对冷却系统进行更深入的研究.目前,冷却系统的发展方向是更趋于智能化和可控化,如调节发动机和汽车的热分布状态;促进冷却介质流动的合理组织性,如冷却介质流动的研究;发动机热管理技术的研究,如应用CFD分析技术和有限元(FEA)耦合分析技术进行数值模拟分析.近年来,随着计算机技术的发展,CFD仿真分析技术广泛应用于发动机散热器的设计,可得到散热器的流通性的信息,还能够直观地模拟系统内液体流动状态,有效地指导散热器的设计工作[1].
本文以汽车发动机冷却水箱C207散热器为研究对象,利用CFD软件STAR-CCM+分析对散热器进行数值模拟,分析散热器换热的性能参数,并优化改进其内部散热片的结构,提高散热器的换热效率.
1 数学模型
1.1 散热过程数学模型
散热器换热是一种由于温差导致冷却液与受热板之间产生流固耦合的换热过程,在使用CFD软件模拟计算时依然要受到守恒定律的支配.基本的守恒定律包括:质量、动量和能量三大守恒定律[3].
质量守恒定律:发生反应前后物质的质量总和不发生改变.质量守恒方程为

(1)
式中:ρ为密度;t为时间;u,v和w为速度矢量u在x、y和z方向的分量.
动量守恒定律:在一个系统中,如果没有受到外力或受到的外力矢量为零,则系统的总动量没有变化.动量平衡方程(N-S方程)为
(2)
式中:ρ是密度;μ是动力粘度;p是微元体上的压力;Su、Sv和Sw是方程中的广义源项,Su=Fx+Sx、Sy=Fy+Sy、Sw=Fw+Sw,而Fx、Fy、Fw是微元体上的体力,一般对于粘性为常数的压缩流体,Sx=Sy=Sw=0.
能量守恒定律:在一个单位体内,能量在转化或转移的过程中能量的总量不会变.以温度T为变量能量守恒方程为
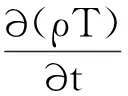
(3)
式中:cp是比热容;T是温度;k是导热系数;ST为内热源及被转化的热能部分.
1.2 参数回归数学模型
在散热器换热过程时,随着温度的不断变化,冷却液的动力粘度和普朗特数也会发生较大的改变.为了提高模拟分析的准确性,对冷却液的动力粘度和普朗特数样本数据进行一元线性回归分析,确定回归数学模型[4].
实际问题中的随机变量Y通常与多个普通变量x1,x2,……xp(p>1)有关.
对于自变量x1,x2,……xp的一组确定值,Y具有一定的分布,若Y的数学期望存在,则它是x1,x2,……xp的函数.
Y关于x的回归函数:
μY|x1,x2,……xp=μ(x1,x2,……xp),
(4)
μ(x1,x2,……xp)是x1,x2,……xp的线性函数.
线性回归模型:
Y=b0+b1x1……+bpxp+ε,ε~N(0,σ2),
(5)
b1,……bp,σ2是与x1,x2……,xp无关的未知参数.
2 模型建立与模拟分析
为了更好地分析冷却系统散热器的换热性能参数,对模型分析的技术要求进行设定:散热器上面板为受热面,材料为铝,温度设为恒温50 ℃;A管道为进水管,温度为15 ℃,B管道为出水管.冷却液为50%浓度的乙二醇溶液,流量为10 L/min;其他所有面均为绝热面.
2.1 散热器几何模型的建立
在对仿真分析结果影响不大的情况下,简化散热器模型的垫圈、支持架、螺钉等零件,用三维建模软件UG建立散热器的实体模型,如图1所示.
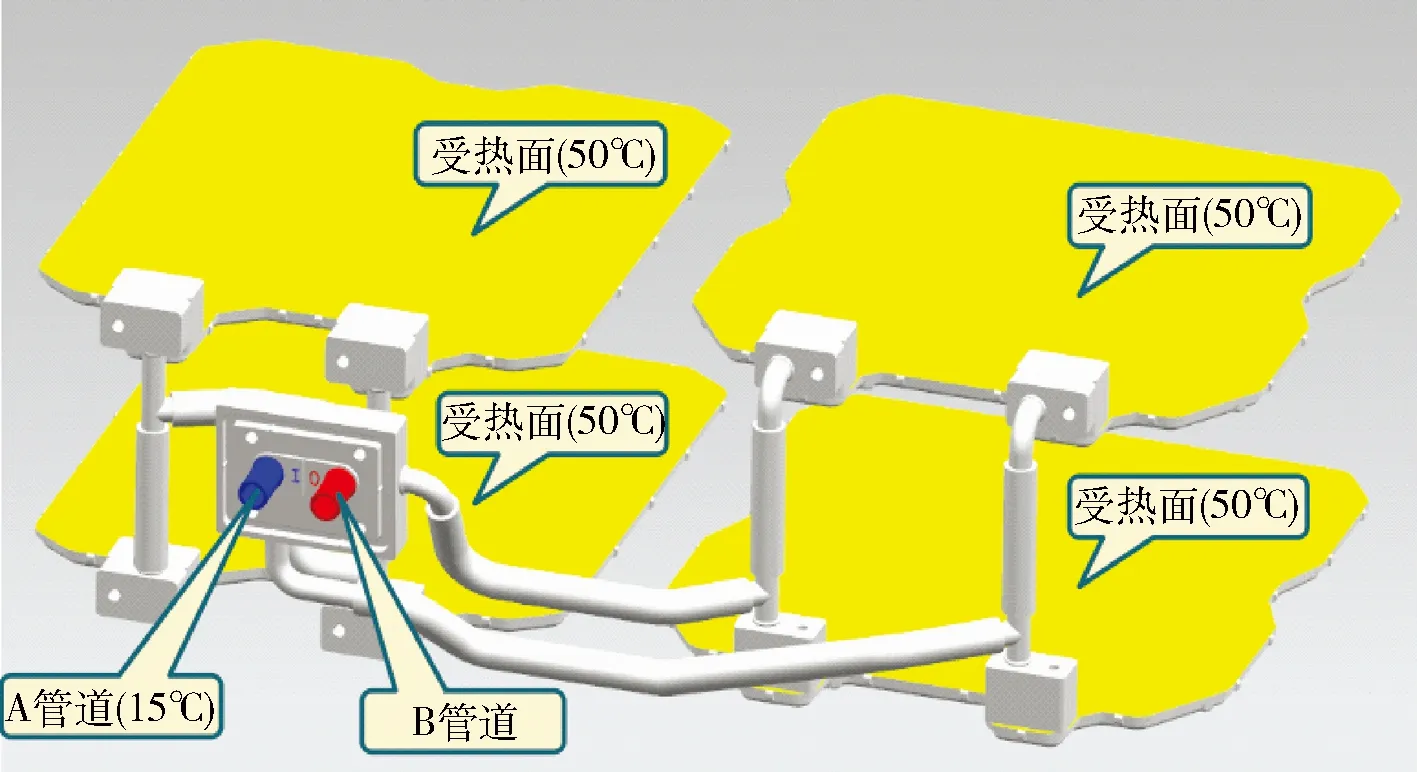
图1 散热器三维实体模型
2.2 网格划分
使用STAR-CCM+软件对模型进行包面处理,将散热器内的流体区域抽出.面网格的质量将直接影响体网格的质量,表面网格准备的越充分,体网格质量越好,因此,要进行表面质量修复处理,改善面网格质量.体网格划分选择切割体网格模型和棱柱层网格模型,切割体网格即六面体网格,其计算精度高且占用计算资源少,缩短计算时间.而棱柱层网格单元更有助于湍流仿真和壁面间的热传递[5].STAR-CCM+软件可以对模型的不同区域分别划分网格,为了保证模拟计算的准确性,为对散热器的内部水道进行网格加密处理.最终计算出的单元网格数量为747.5万,如图2.

图2 散热器网格图
2.3 设定边界条件
1)入口边界条件
在此散热器模型中,设置入口边界条件为质量流量入口,根据技术条件的进口流量为10 L/min,进行转换后的流量为0.167 77 kg/s,设置入口物理条件温度为15 ℃.
2)出口边界条件
散热器的出口只有一个,在模拟中采用压力出口,出口环境温度为26.85 ℃.
3)流体属性设置
流体物理模型设为定常、恒密度,流体状态为不可压缩、湍流模型.不同的湍流模型对流体流动的分析结果影响很大,本文采用标准K-Epsilon湍流模型能够较准确地模拟复杂曲线形状管道内的湍流运动[6-7].模型中选用的冷却液为50%浓度乙二醇溶液,因此,需要设置冷却液的物理属性,如表1为50%浓度乙二醇溶液的物理属性.

表1 50%浓度乙二醇溶液的物理属性
普朗特数和动力粘度随温度的变化有较大幅度的波动,需要查阅50%浓度乙二醇溶液的动力粘度和普朗特数的变化数值[8-9],如表2.运用MATLAB软件的regress函数进行线性回归分析,并得出散点图和回归函数,回归函数的拟合优度系数为0.962 8,拟合程度较高.将回归函数导入STAR-CCM+中,以自定义场函数的方式作用到模拟分析中[10],STAR-CCM+软件中的场函数功能能够实时监测任意物理量的变化,即可以反映实际流动参数.
动力粘度的场函数方程为
μ=5.523 571-0.079 571×(T-273.15).
(6)
普朗特数的场函数方程为
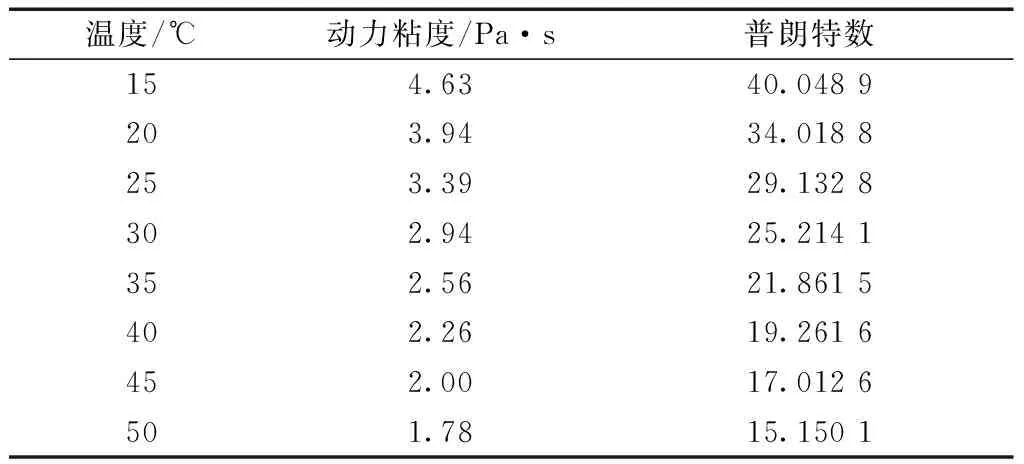
Pr=47.830 226-0.695 926×(T-273.15). (7)
2.4 定义求解器和后处理参数
在STER-CCM+中使用衍生平面截取4个取值分析的位置,分别为上侧截面Z1= 0.055 m,下侧截面Z2=-0.088 m.通过衍生平面可以更好的观察温度场、压力场、速度场的变化云图.建立压降报告,求解其入口和出口压力差,判断散热器内部冷却液的流动情况[11].建立平均质量流量和表面平均值报告,当迭代计算收敛后,可监测入口和出口的压力、温度和速度的准确数值.建立热传递报告,可分析出散热器流固耦合的热转换效率.求解器参数保持软件默认状态,停止标准设置为1 000步.
3 计算结果分析
经过STAR-CCM+软件迭代计算完成后,压力、温度监测值均趋于稳定,残差已经得到收敛.通过查看温度场、压力场、速度标量场和矢量场云图得出分析结果.
从温度场景中可以看到模型的入口处温度最低,为15 ℃,经过与恒温50 ℃的受热板热交换后的冷却液出口温度在29 ℃左右.如图3为场景分布云图.在压力场景中,入口处的压力值最大,压力值距离A管道越远并逐步递减.从速度标量云图和矢量云图中可以看出冷却液的速度值范围较为均匀,在0.15 m/s-0.3 m/s之间,说明冷却液的流动较为顺畅.当模型迭代计算到150步左右,热传递功率就趋于稳定,如图4为热传递功率图.散热器计算结果具体参数如表3.

图3 场景分布云图
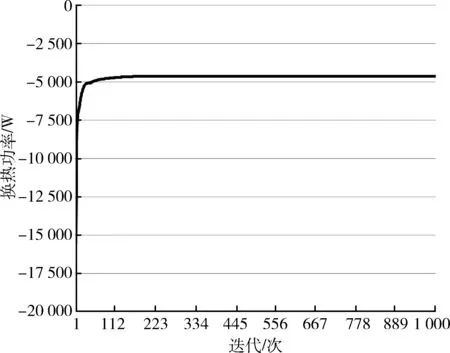
图4 热传递功率图
表3 散热器分析结果

参数分析结果出口温度/℃23.68压差/Pa7719.4换热功率/W4512.2进口速度/(m·s-1)1.511出口速度/(m·s-1)1.510
4 散热器结构优化与分析
4.1 优化方案
在此研究模型中,冷却液和受热板的材料属性、冷却液的流动速率和冷却液与受热板之间的换热面对散热器的换热效率有较大的影响.现冷却液和受热板的材料属性、冷却液的流动速率暂不能发生改变,若要进一步提高散热器的换热效率,需要促进冷却液与受热板之间的相互接触,结构优化如下:将散热器散热片的波纹状结构改进为栅格状结构,如图5所示.

图5 散热片结构优化示意图
4.2 优化结果分析对比
在改进优化后两个研究方案进行对比中,从场景图中可以发现细微的差别,如图6为优化后的场景云图.在温度场云图中对比发现冷却液温度变化明显加快,在速度场景云图中对比发现冷却液流速稍有变缓.从数据报告中可以得到更加细致、准确的数据.在出口温度对比中,优化后的方案出口温度更高,大约提高了4.1%,说明冷却液在热交换中吸收的热量增加了.在进出口速度对比中,进出口速度分别下降了1.1%和0.86%,这说明散热器结构优化使内部流动体积增大导致流速降低了.而进出口的压力差较优化前也下降了2.9%,说明散热器内部流动阻力有所降低,冷却液的流动更为顺畅.在优化后的方案中换热功率也有了一定的提高,换热功率提高了24.2%,如图7为热传递功率图.计算结果具体参数对比如表4.
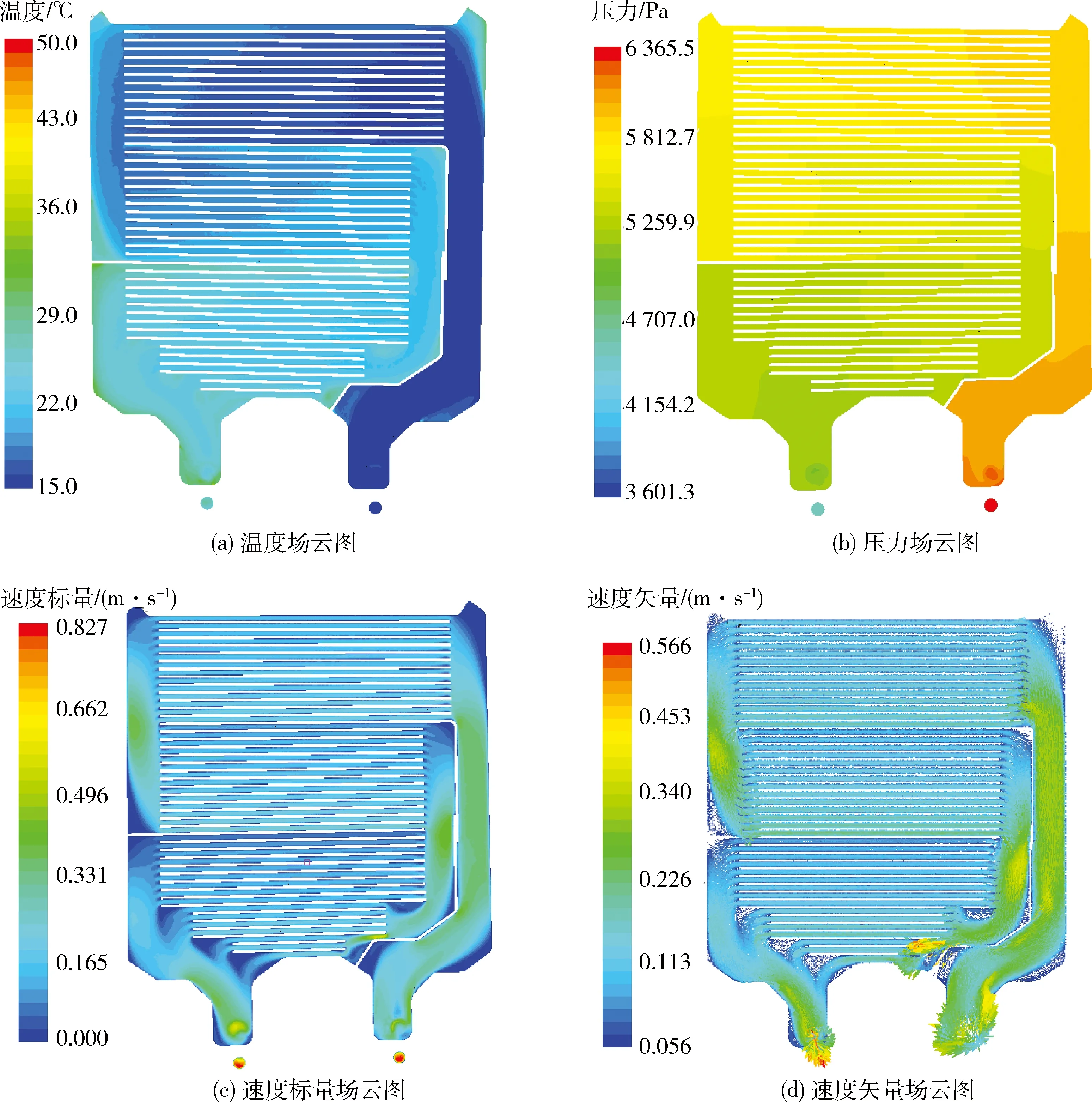
图6 优化后的场景云图
图7 热传递功率图
表4 优化前后结果对比
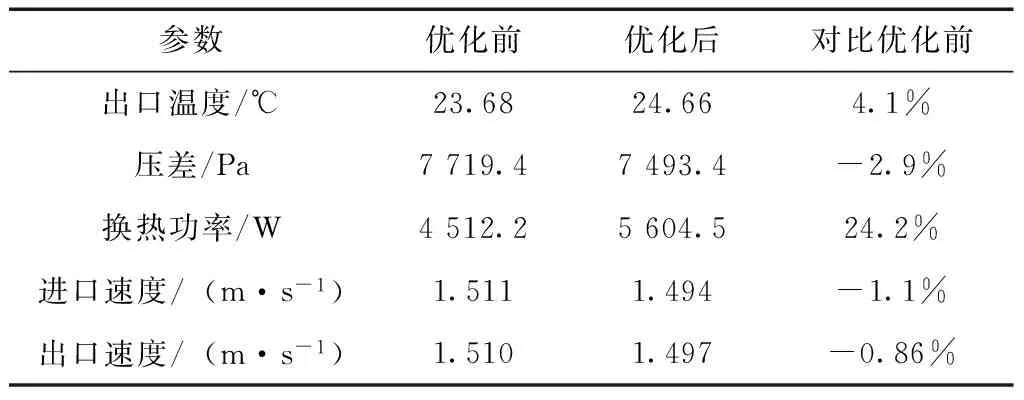
参数优化前优化后对比优化前出口温度/℃23.6824.664.1%压差/Pa7719.47493.4-2.9%换热功率/W4512.25604.524.2%进口速度/(m·s-1)1.5111.494-1.1%出口速度/(m·s-1)1.5101.497-0.86%
对优化前与优化后散热器横截面进行对比验证,波纹状散热片的横截面体积大于栅格状散热片的横截面体积,因此,栅格状结构散热器能够进一步提高换热效率,则此次的散热器改进优化是成功的.通过对冷却系统的内部结构优化可以一定程度提高换热速率,若想进一步提高其换热速率,可以改变冷却液和受热板的材料、改变冷却液的物理属性或提高冷却液的流量等方法[12].
5 结 论
应用CFD软件STAR-CCM+对C207冷却系统散热器进行数值模拟分析,获得了模拟散热器工作时的压力场、温度场和速度场的分布情况以及散热器的传热功率.为研究分析散热器热传递优化设计提供了参考依据.
本文采用线性回归的方法对冷却液的特性参数进行设定,并自定义场函数导入到STAR-CCM+中,这种方法使计算结果更为准确;通过对散热器原有结构进行优化改进,将波纹状结构的散热片改进成栅格状结构,有效降低了散热器的流动阻力,提高了冷却液质量流量,使散热器的换热效率提高了24.2%.
运用CFD仿真技术可以指导产品设计开发及优化,为方案的确定及性能的评价提供重要的依据,从而提高了设计效率.
[1] 叶建伟,陈小东. 基于STAR-CCM+发动机进气歧管CFD分析及优化[J]. 内燃机,2016,32(1):4-6.
[2] 丁 攀. 电子节温器的设计与控制策略研究[D]. 沈阳:沈阳理工大学,2013.
[3] 李 军,武 磊,向 璐. 基于STAR-CCM+进气歧管的稳态CFD分析[J].湘潭大学自然科学学报,2015,37(2):97-100.
[4] 李艳娇,李瑞敏,陈经伟. 多元线性回归的MATLAB实现[J].常熟理工学院学报,2014(2):49-52.
[5] 孟庆林,尹明德,朱朝霞. 基于STAR-CCM+的发动机冷却风扇CFD仿真分析[J].南京航空航天大学学报(自然科学版),2015,28(3):60-63.
[6] Anja T, Gareth F, Chris M. A CFD study of fuel evaporation and related thermo-fluid dynamics in the inlet manifold, port and cylinder of the CFR octane engine[J].SAE International Journal of Fuels and Lubricants,2012(3):1264-1276.
[7] David Chalet, Pascal Chesse. Fluid dynamic modeling of junctions in internal combustion engine inlet and exhaust systems[J].Journal of Thermal Science, 2010,19(5):410-418.
[8] 张少君.乙二醇型汽车发动机冷却液的检测和正确使用[J]. 应用基础与工程科学学报,2012,20(9): 68-70.
[9] 宋兴福,罗 妍,汪 瑾,等. 甲醇-乙二醇二元混合液密度和粘度的测定及关联[J]. 华东理工大学学报(自然科学版),2007,33(6):750-753.
[10]Luther N J. An experimental investigation of the flow over the rear end of a notchback automobile configuration[J].SAE Transactions,2000,109(6):680-701.
[11]唯利铭,刘 庆. 基于STAR-CCM+的防爆柴油机水冷式排气管数值模拟分析[J]. 河南机电高等专科学校学报,2015(2):19-23.
[12]田杰安,李世伟,闰 伟. 基于CFD分析的散热器结构优化[J]. 内燃机与动力装置,2012,29(4):40-43.
Heat Transfer Analysis and Structure Optimization of AutomobileRadiator Based on STAR-CCM+
XU Xiao-wen1, SUN Hou-huan1, HUA Guang-sheng2
(1. School of Mechanical and Power Engineering, Nanjing Tech University, Nanjing 210000, China;2. China National Accreditation Service for Conformity Assessment,Beijing 100000, China)
Taking a radiator, Model C207, of the cooling tank from an automobile engine as the research object, its modal analysis of the fluid-structure interaction was carried out in STAR-CCM+. Based on the linear regression analysis, a regression model of the coolant parameters was determined and then a user-defined field function was imported into the model. By means of a standard K-Epsilon turbulence model, the changes in temperature, pressure and velocity were analyzed of the coolant in the radiator. In order to improve the heat transfer efficiency, the structure of the radiation fins was optimized and a better effect in heat transfer was obtained.
computational fluid dynamics; linear regression analysis; radiator; STAR-CCM+
1009-4687(2017)02-0044-06
2017-1-9
江苏省第九批六大人才高峰高层次人才资助项目(项目编号:2012-ZBZZ-047)
许晓文(1992-),男,硕士研究生,研究方向为发动机CFD数值模拟.
TH16,U463
A
