一种用于蒙特卡罗仿真的风速相关性变换方法

(国网北京房山供电公司，北京 100031)

1 引言

大量研究表明，风速的相关性对电网的运行和可靠性等方面会产生重大影响，文献[3-4]的研究表明考虑风速的相关性会使风电场并网点的电压和相关支路传输功率的波动更加剧烈、电压越限的概率增大，支路传输功率则可能会在风速强正相关性时出现过载现象，进而影响概率潮流的计算；文献[5]指出风速的相关性对节点电价有一定的影响，特别是对实时电价的影响尤为突出；文献[6]指出随着风电场相关系数的增加，风电场有功出力范围增大，最优潮流结果的波动范围也随之增大；文献[7-8]的研究显示风电场间的相关性对系统可靠性水平有不利影响，并且随着风电场装机容量的增大，其影响越明显。

从上述分析可知，研究风电需要考虑风速的相关性，但这其中需要解决的主要的问题是如何模拟具有相关性风速。目前用来模拟风速相关性的一个最普遍的方法是线性矩阵变换技术[9-11]，该方法原理简单、易于实现，但是其在产生具有指定相关性的抽样序列时，默认其服从正态分布，但大量研究表明风速的变化规律服从威布尔分布[12]，因此该方法会产生较大误差。为了解决此问题，文献[13]采用三阶多项式变换技术构建了一个可以处理非正态分布的多变量最优潮流蒙特卡罗模拟模型，文献[14]通过反变换法完成正态分布与非正态分布之间的转换，包括相关性结构的转换，这两个方法虽然能解决风速非正态分布的问题，但非正态变换算法比较复杂，难以实现，而且这两个方法均未考虑随机抽样对原始风速抽样矩阵相关性的影响，其模拟的精度不高。

针对上述问题，本文提出一种实用的风速相关性变换方法，该方法用到Gram-Schmidt序列正交化算法和Cholesky分解算法，其中，前者主要用来消除或大大降低原始风速矩阵的相关性(正交化)，从而减少随机抽样的影响；后者主要用来把正交化的风速矩阵变换成具有给定相关性的风速矩阵；由于Gram- Schmidt序列正交化法和Cholesky分解法均是通过改变风速矩阵中元素的排列顺序来间接改变其相关性的，其可以在满足相关性要求的同时最大程度的保留各风电场风速的概率分布特性。

2 常规变换方法

对大量实测风速数据的统计结果表明，风速的变化规律服从两参数的Weibull分布，用随机变量V代表风速的大小，则其分布函数可表示为：

(1)

其中，Wk为形状参数；Wc为尺度参数，其值反映该风电场的平均风速；V代表给定风速，单位是m/s。

在均匀分布的[0，1]中抽取随机数U，并令，

(2)

由式(2)把风速V解出来，并整理得：

V=Wc)-ln)U′))1/Wk

(3)

式中，U′=1-U为在[0，1]区间均匀分布的随机数。

对于m个相关的风电场，假设对每个风电场的风速分别进行N次随机抽样，则所得的风速序列可构成一个m×N阶矩阵，记为VmN，其中矩阵的每一行代表一个风电场的风速序列。当考虑多个风电场，特别是处于同一个风带的风电场同时接入被评估的电力系统时，需要考虑他们之间的相关性。以风速矩阵VmN为例，一种简单的常规变换方法为：

(4)

3 本文变换方法

为了精确模拟各风电场风速之间的相关性，本文引入Gram-Schmidt序列正交化算法和Cholesky分解算法，下面简单介绍这两个算法的原理。

Gram-Schmidt序列正交化方法：该方法能得到比其他方法更低的相关性，而且该方法可以根据处理问题的要求而实现不同精度的相关性。其基本原理为：对于一个K×N阶的抽样矩阵XKN，构造一个K×N阶的排列矩阵LKN，该矩阵的每一行的元素值代表抽样矩阵XKN中对应行元素的排列位置。应用Gram-Schmidt序列正交化方法来降低抽样矩阵XKN中行之间的相关性的基本步骤为：首先生成一个K×N阶的初始排列矩阵LKN，其每一行的元素都是整数1，2，…,N的随机排列，然后进行如下正向和反向迭代过程。

正向：

forj=2,3,…,K

fori=1,2,…,j-1

Li←takeout(Li,Lj)

Li←rank(Li)

(5)

反向：

forj=K-1,K-2,…,1

fori=K,K-1,…,j+1

Li←takeout(Li,Lj)

Li←rank(Li)

(6)

其中，“←”表示赋值；对于给定的行向量Li和Lj，takeout(Li，Lj)表示计算线性回归Li=a+bLj(a和b为线性回归计算出的值)中的残差值；rank(Li)表示取向量Li中元素的从小到大的排列序号形成的新向量。

Cholesky分解法：对于行相关性很小的抽样矩阵XKN及其排列矩阵LKN，假设给定的相关系数矩阵为ρXref，可以证明ρXref是一个K×K阶的正定对称矩阵，因此用Cholesky分解法对其分解可以求得一个实数的非奇异下三角矩阵D，并满足如下等式：

(7)

结合排列矩阵LKN可以构造一个新的矩阵：

GKN=DLKN

(8)

GKN即为新构造出来的排列矩阵。

4 算例分析

4.1 算例描述

在MATLAB R2011中编制相关程序和算法，对IEEE-RTS79测试系统进行计算分析，该系统包含24条母线、32台发电机组和5个变压器，总装机容量为3405MW，基本年负荷峰值为2850MW。

为了分析风速相关性对系统可靠性的影响，设计3个相关风电场，其中风电机组的单机容量均为1.5MW，其切入风速、额定风速和切出风速分别为3m/s、10m/s和25m/s； 3个风电场的风速均服从两参数的威布尔分布，其中Wc=8、Wk=2，相关系数η12=η21=0.1、η13=η31=0.1和η23=η32=0.2；风电场的可靠性参数如表1所示。

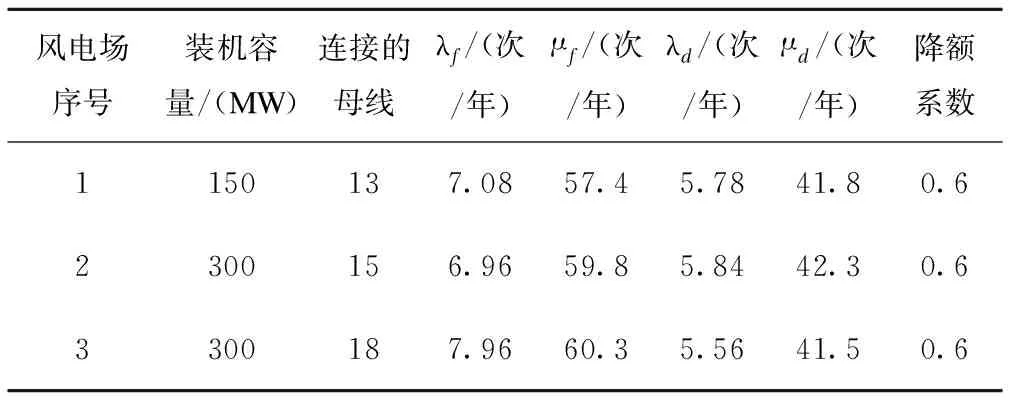
表1 风电机组的参数

4.2 方法验证

4.2.1 相关性变换精度的验证

由于蒙特卡罗方法是波动收敛的，其精度具有一定的随机性，为了消除其影响，令常规方法和本文方法各仿真20次，结果如图1、2和3所示。

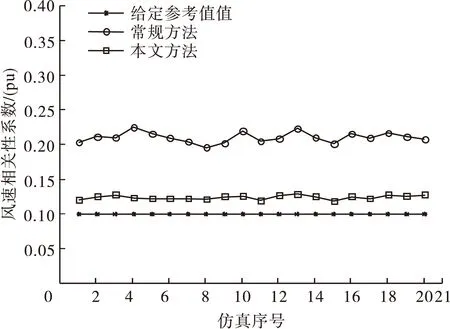
图1 风电场1和2之间的风速的相关系数

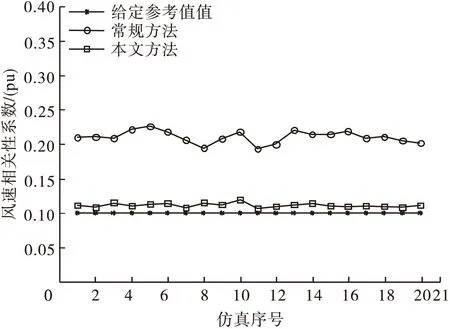
图2 风电场1和3之间的风速的相关系数

图3 风电场2和3之间的风速的相关系数

图1、2和3分别为风电场1与2、1与3和2与3之间的相关系数的仿真结果，其主要反应两个风电场之间相关性的大小，其中，表示给定的参考值，表示采用常规方法处理后的相关系数，示采用本文方法处理后的相关系数；从中可以明显看出，采用本文方法得到的相关系数更接近参考给定值，既：具有较高的精度。

5 结论

通过对含3个风电场的改进IEEE-RTS79算例的仿真和研究，得到如下结论：

所提出的风速相关性的变换方法可以达到较高的精度和较强的稳定性，同时由于该方法是通过改变风速矩阵中元素的位置而间接改变其相关性的，因此还可以最大程度的保留风速的概率分布特性，从而提高评估的可信性和精度。

[1] 于大洋,韩学山,梁军,等.基于 NASA 地球观测数据库的区域风电功率波动特性分析[J].电力系统自动化,2011,35(5):77-81.

[2] 肖创英,汪宁渤,丁坤,等.甘肃酒泉风电功率调节方式的研究[J].中国电机工程学报,2010,30(10):1-7.

[3] 邓威,李欣然,徐振华,等.考虑风速相关性的概率潮流计算及影响分析[J].电网技术,2012,36(4):45-50.

[4] 简金宝,刘思东.风速空间相关性和最优风电分配[J].电力系统保护与控制,2013,41(19):110-117.

[5] Morales J M,Conejo A J,Perez-Ruiz J.Simulating the impact of wind production on locational marginal prices[J].IEEE Transactions on Power Systems,2011,26(2):820-828.

[6] 潘雄,周明,孔晓民,等.风速相关性对最优潮流的影响[J].电力系统自动化,2013,37(6):37-41.

[7] 吴林伟,张建华,刘文霞,等.考虑风速相关性的电力系统可靠性评估[J].华东电力,2013,41(10):2009-2012.

[8] 秦志龙,李文沅,熊小伏.考虑风速相关性的发输电系统可靠性评估[J].电力系统自动化,2013,37(16):47-52.

[9] Feijoo A E,Cidras J,Dornelas J L G.Wind speed simulation in wind farms for steady-state security assessment of electrical power systems[J].IEEE Transactions on Energy conversion,1999,14(4):1582- 1588.

[10] 王海超,鲁宗相,周双喜.风电场发电容量可信度研究[J].中国电机工程学报,2005,25(10):103-106.

[11] 蔡德福,陈金富,石东源,等.风速相关性对配电网运行特性的影响[J].电网技术,2013,37(1):150-156.

[12] 丁明,吴义纯,张立军.风电场风速概率分布参数计算方法的研究[J].中国电机工程学报,2005,25(10):107-110.

[13] 杨欢,邹斌.含相关性随机变量的概率最优潮流问题的蒙特卡罗模拟方法[J].电力系统保护与控制,2012,40(19):110-115.

[14] 秦志龙,李文沅,熊小伏.含具有风速相关性风电场的发输电系统可靠性评估[J].电力系统保护与控制,2013,41(20):27-33.