低度欠膨胀超音速圆盘止推气体轴承缝隙射流的数值模拟

郭良斌，张一帆

(武汉科技大学机械自动化学院，湖北 武汉，430081)



低度欠膨胀超音速圆盘止推气体轴承缝隙射流的数值模拟

郭良斌，张一帆

(武汉科技大学机械自动化学院，湖北 武汉，430081)

采用SSTk-ω湍流模型，对高压圆盘气体轴承出流气体形成的低度欠膨胀超音速圆盘缝隙射流流场进行数值模拟。结果表明，低度欠膨胀超音速圆盘射流起始段1的流场波系，与低度欠膨胀超音速轴对称射流类似；起始段2中由于黏性作用逐渐深入核心区，使核心区宽度持续减小。进入亚音速基本段之后，核心区消失，射流对称面上速度持续下降，直至出现滞止区。与此同时，缝隙射流发生规则分离，两股气流偏离滞止区向两侧流动，在射流左右两侧的远场形成规则对称的两个大尺度环状漩涡。

圆盘止推气体轴承；超音速射流；缝隙射流；欠膨胀；流场分析；数值模拟

传统结构的静压气体轴承存在承载力小、刚度低的缺点，仅适用于轻载精密支承。然而随着航空航天等高新技术的发展，迫切需要开发高压重载气体润滑轴承。20世纪80年代中期，日本学者Miyake等[1-3]提出了超音速圆盘止推气体轴承的概念，并进行了理论与实验研究，但是其理论预测与实验结果吻合度较差，反映出其采用的一维气体动力学模型并不能较好地模拟轴承间隙中气体的实际流动情况。徐凡[4]借鉴风洞收缩段壁面曲线的相关设计理论，设计了适用于向高压圆盘止推气体轴承供气的双对称“收缩段”，完成了供气孔与气膜间隙之间的型面过渡，改善气膜内部流场的同时，气体以超音速流出气膜间隙，喷入周围环境，形成一种超音速圆盘缝隙射流，但其仅讨论了高压轴承内部流道的流场特性，没有研究缝隙射流的特性。

高压圆盘气体轴承出流气体的出口速度高、温度低，形成的射流主要沿圆盘径向流动，而一般的轴对称射流主要沿喷管轴线流动，两者可能具有不同的波系结构。欠膨胀轴对称超音速射流流场存在着较强的马赫波放射，而马赫波辐射与射流噪声的啸叫存在着密切联系[5]。人员在不同噪声声级中暴露的时间不能超过安全标准[6]，否则会对听觉造成损伤。因此，研究和掌握超音速圆盘缝隙射流的流场特性，是进一步抑制高压气体轴承噪声，保证轴承实验人员安全操作的基础。

目前，国内外学者对超音速射流的研究多着眼于轴对称超音速射流流场[7-10]，较少见到针对超音速圆盘缝隙射流的专门报道。超音速射流中，波系结构最规则的是低度欠膨胀射流，因此本文采用SSTk-ω模型，针对低度欠膨胀圆盘缝隙射流的流场特性展开研究。

1 控制方程及湍流模型

1.1 控制方程

圆盘缝隙射流与轴对称射流的数学模型形式相同，但两者的流场结构不同。如图1所示，轴对称射流主要沿轴向(即z方向)流动，圆盘缝隙射流主要沿径向(即r方向)流动。

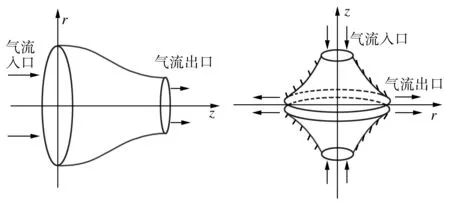
(a)轴对称射流 (b)圆盘缝隙射流

图1 两种不同射流的坐标系

Fig.1 Two different jets’ coordinates

可压缩二维圆盘缝隙射流的控制方程为

(1)

式中：Q为求解变量，Q=(ρ,ρu,ρv,e)T，其中ρ为密度，u、v分别为流体在z向和r向的速度，e为内能；t为时间；E、F分别为z向和r向的无黏通量；Ev、Fv分别为z向和r向的黏性通量；H为源项。

1.2 湍流模型

SSTk-ω湍流模型通过对输运方程的改进使其计算轴对称超音速射流流场时有较高的准确性[11]。SSTk-ω模型在BSLk-ω模型的基础上，考虑湍流黏性作用下的湍流剪应力μt，其涡黏性模型方程如下：

(2)

2 仿真计算

2.1 几何模型

带有双对称收缩段的高压平行圆盘止推气体轴承结构简图如图2所示。具体结构尺寸为：a=6.2486 mm，b=0.3 mm，c=90 mm，e=60 mm，f=32.05 mm。

由于该轴承具有柱对称结构，为减少计算量，取轴承结构的半剖面(图2中z轴左边部分)进行计算。

a—供气孔直径；b—气膜间隙；c—轴承半径；e—平行段长度；f—供气孔的高度

Fig.2 Circular thrust gas bearing with disymmetric contraction cones

2.2 边界条件与参数设置

基本边界类型设置如图3所示。壁面取无滑移壁面条件；AB是圆盘轴线；AF、BC取为压力入口，通过对多种总压比的数值模拟结果进行分析，入口压力取1.317 225 MPa时，能较好地反映低度欠膨胀超音速圆盘缝隙射流的特性，故算例中入口压力取为1.317 225 MPa；DE为气膜间隙出口；射流计算域为EHILKJGD，将EI、IL、DJ、JK计算边界设置为壁面边界条件；LK为压力出口，压力设置为0.101 325 MPa。IJ长度为DE的500倍以上，IL为DE的700倍以上。

图3 边界条件设置

流体密度采用满足理想气体状态方程的理想气体密度，黏度系数符合Sutherland公式；AF、BC压力入口的气体总温与LK压力出口的气体总温均为300 K；湍流强度为7%；采用SIMPLE压力速度耦合方式进行计算。

采用Icem软件进行网格划分，图3所示的计算域中共划分网格约92万个，其中收缩段及间隙出口附近网格图如图4所示。

流道收缩段内的流场较为复杂，网格划分得较为密集。为了较为精确地获得流场参数，对轴承流道近壁面的8层网格进行加密，收缩段内加密的总厚度为0.07a，间隙内加密的总厚度为0.07b，如图4(a)所示。

(a)收缩段网格图

(b)轴承间隙出口网格图

轴承外部射流在出口处沿z方向变化梯度大。因此外部射流区域中沿z方向，网格划分采用由密到稀的方法，如图4(b)所示。

2.3 数值模拟方法的可行性分析

为验证本文所用SSTk-ω模型及计算方法对圆盘缝隙射流流场的适用性，将其计算结果与文献[12]中的实验结果及采用Realizablek-ε模型计算的结果进行比较。

以文献[12]中图2(b)所研究的单供气孔气体轴承超音速流场为例，气膜间隙h分别为25.4、50.8、127 μm时，2种方法与实验结果的对比如图5所示。从图5中可以看出，采用Realizablek-ε模型和SSTk-ω模型均能较好地反映气膜内超音速流场的流动趋势，且 SSTk-ω模型与实验结果更为吻合，故本文用SSTk-ω模型进行数值求解是可行的。

图5 两种数值方法与文献[12]所给实验结果的对比

Fig.5 Numerical results compared with experiment results of paper [12]

3 仿真结果分析

参照文献[13]中图8-20对轴对称低度欠膨胀超音速射流起始段和基本段的划分方法，将圆盘缝隙射流(以下简称“射流”)中包含核心区的部分称为起始段，核心区被完全湮没的部分称为基本段。将起始段又划分为两个部分，其中第一波节结束前的部分称为起始段1，第一波节后的部分称为起始段2。

3.1 射流起始段的流场分析

射流起始段的速度矢量、马赫数等值线及压力等值线如图6所示。

从图6(a)中可观察到，在起始段1中，气流流出缝隙时，由于存在膨胀波的作用，超音速核心区的宽度先短暂扩张，后又开始减小，这是由膨胀波从核心区两边声速线上反射回来的压缩波的作用造成的。此扩张收缩过程与轴对称低度欠膨胀射流流出喷口时的膨胀波-压缩波交替过程相似。由图6(b)可知，从核心区向两侧，马赫数从声速连续减小，表明在低度欠膨胀条件下，超音速圆盘缝隙射流的射流边界层是亚音速的，与轴对称低度欠膨胀射流的边界层[13]相似。气体流出缝隙时，超音速核心区马赫数先增加，然后减小，直到第一波节结束。从图6(c)可以看出，缝隙出口压力约为0.1317 MPa，略大于环境压强。结合第一波节中波系结构的分析结果可知，起始段1流场符合低度欠膨胀射流的典型特征。

(a)速度矢量图

(b)马赫数等值线图

(c)压力等值线图

随着射流继续向前，从图6(a)可以看出，起始段2中边界层逐渐加厚，黏性作用进一步向核心区渗透，核心区的宽度逐渐减小。从图6(b)可以看出，起始段2中仍然存在膨胀波和压缩波的作用，但由于核心区宽度的减小，后续波节不太明显。

射流刚从缝隙出口流出时，亚音速射流边界层很薄，此时在射流边界层内存在很大的速度梯度，相应在射流边界上黏性的影响非常剧烈。黏性影响逐渐向射流边界的内外两侧发展，当整个截面上都变为黏性边界层后，随着气流继续向前流动，由于黏性的作用，各点的流速均下降，一直到变为亚音速射流。

3.2 射流基本段流场分析

射流基本段内的马赫数等值线如图7所示。从图7可以看出，当进入亚音速基本段以后，随着气体继续向前流动，核心区消失，射流对称面上的速度与两侧边界层中的速度差异逐渐被拉平，直到该位置处的速度低于附近两侧射流边界层中的最大流速。随着气流继续向前流动，射流对称面上速度持续下降，出现速度为零的滞止区，气流开始分为两股并偏离滞止区。

图7 射流基本段马赫数等值线图

3.3 全场射流流场分析

射流区域全场的马赫数等值线如图8所示。由图8中可见，当基本段气流出现规则分离后，射流分为两股，流动方向朝两侧偏折一定角度。每股气流向斜上方流动时，与射流边界层外的环境气体发生剪切作用，在射流左右两侧的远场形成规则对称的两个大尺度环状漩涡，漩涡中心距离缝隙的出口较远。远场规则对称的环状漩涡是圆盘缝隙射流的特有现象，尽管平面缝隙射流的射流边界上也存在尺度不一的大、小漩涡，但这些漩涡呈不规则分布，是由紊动涡体和周围流体交错组成的[14]。

图8 射流全场马赫数等值线图

4 结论

(1)低度欠膨胀超音速圆盘缝隙射流，起始段波系结构与轴对称低度欠膨胀射流起始段相似。低度欠膨胀条件下，超音速圆盘缝隙射流的射流边界层是亚音速的，与轴对称低度欠膨胀射流的边界层相似。

(2)起始段2中由于黏性作用逐渐深入核心区，使核心区宽度持续减小。

(3)进入亚音速基本段之后，核心区消失，射流对称面上速度持续下降，直至出现滞止区。

(4)基本段气流出现规则分离后，射流分为两股，流动方向朝两侧偏折一定角度，每股气流向斜上方流动时，在射流左右两侧的远场，形成规则对称的两个大尺度环状漩涡。

[1] Miyake Y, Inaba T, Hibi M. An externally pressurized supersonic gas thrust bearing (1st report, static characteristics in supersonic operations)[J]. Journal of Tribology, 1984, 106:163-168.

[2] Miyake Y, Inaba T, Matsuoka T. An externally pressurized supersonic gas thrust bearing (2nd report, dynamic characteristics in supersonic operations and static characteristics in sonic operations)[J]. Journal of Tribology, 1984. 106:169-173.

[3] Miyake Y, Inaba T, Kubo N, et al. An experimental study on externally pressurized supersonic gas thrust bearings[J]. Journal of Tribology, 1985, 107:122-127.

[4] 徐凡.高供气压圆盘止推轴承设计理论研究及实验[D]. 武汉：武汉科技大学，2016.

[5] 杨京龙，何枫.超声速射流流场及噪声特性的实验研究[C]//第七届全国实验流体力学学术会议论文集:A集.北京:中国力学学会(CSTAM),2007:5-11.

[6] 张贵林. 某火箭发射系统发射过程人员安全性研究[D]. 南京：南京理工大学, 2010.

[7] 何枫，谢峻石，姚朝晖. 超声速欠膨胀冲击射流的数值模拟[J].推进技术, 2002,23(2):96-99.

[8] 杨风波，马大为，乐贵高，等.基于AUSM改进格式的超声速射流数值模拟[J].弹道学报, 2014,26(4):88-93.

[9] Golovanov A N, Pakhomov F M. Supersonic axisymmetric flow past a blunt cone executing longitudinal low-frequency oscillations[J]. Fluid Dynamics, 2014, 49(1):108-111.

[10]Silnikov M V, Chernyshov M V, Uskov V N. Two-dimensional over-expanded jet flow parameters in supersonic nozzle lip vicinity[J]. Acta Astronautica, 2014, 97:38-41.

[11]朱伶枫，张延玲，朱荣，等. 超音速射流流场湍流模型适应性研究[J]. 太原理工大学学报, 2015,46(1):49-54.

[12]Eleshaky M E. CFD investigation of pressure depressions in aerostatic circular thrust bearings[J]. Tribology International, 2009, 42:1108-1117.

[13]赵承庆，姜毅.气体射流动力学[M].北京：北京理工大学出版社，1998:129-132.

[14]刘荣华.综采工作面隔尘理论及应用研究[D].长沙：中南大学，2010.

[责任编辑 郑淑芳]

Numerical simulation of low-unexpanded supersonic disk slot jet flow of a circular thrust gas bearing

GuoLiangbin，ZhangYifan

(College of Machinery and Automation, Wuhan University of Science and Technology,Wuhan 430081, China)

With the SST k-ω turbulence model，numerical simulation was carried out of low-unexpanded supersonic disk slot jet flow， which was formed by outflow gas of a high-pressure circular thrust gas bearing. The calculated result indicates that the wave system in initial segment 1 of supersonic disk slot jet flow field is similar to that of low-unexpanded supersonic axisymmetric jet flow. In initial segment 2, as viscosity moves deeper into the jet core area, the width of the jet core area is gradually reduced. After entering the subsonic basic section, the core zone disappears and velocity in symmetrical plane of jet continues to decline, until the stagnation zone emerges. At the same time, slot jet is separated into two streams regularly, which deviate from the stagnation zone and flow to both sides. Finally, in the far field beside the jet two regular symmetry large scale annular eddies are formed.

circular thrust gas bearing; supersonic jet flow; crack jet; under-expanded; flow field analysis; numerical simulation

2017-02-23

国家自然科学基金资助项目(51475341).

郭良斌(1973-)，男，武汉科技大学教授，博士.E-mail:guoliangbin@sina.com

10.3969/j.issn.1674-3644.2017.04.009

TH133.36；TH117.2

A

1674-3644(2017)04-0285-05