基于VIKOR的再制造服务供应商选择决策方法

夏绪辉，胡俊峰，王 蕾

(武汉科技大学机械传动与制造工程湖北省重点实验室，湖北 武汉，430081)



基于VIKOR的再制造服务供应商选择决策方法

夏绪辉，胡俊峰，王 蕾

(武汉科技大学机械传动与制造工程湖北省重点实验室，湖北 武汉，430081)

再制造服务是实现产品多生命周期的重要运行管理模式之一。本文针对再制造服务活动及其组合方式，构建了一种以供应商匹配决策为主导的三阶段再制造服务过程模型。为解决供应商决策中评价信息的复杂性和不易量化的问题，引入区间数、语言变量、模糊数等多种数据类型进行信息描述，保持了数据的真实性和实用性；针对主、客观两种评价准则下的混合数据类型评价信息，运用VIKOR方法对备选方案择优排序，克服了混合数据的不可公度性和数据转换导致的失真问题，得到的妥协最优解更符合企业实际需求；运用信任函数和熵权法来确定决策者和各准则的权重，避免主观赋权的二次不确定性。最后通过算例和敏感性分析验证了所提出的供应商选择方法的可行性和稳定性。

再制造服务；供应商选择；VIKOR方法；多准则群决策；模糊数；熵权法

随着世界经济模式从产品经济向服务经济转型，服务业与传统制造业逐步融合。再制造作为传统制造的拓展[1-2]，也需要以服务化运作模式来满足其个性化服务需求，以不断扩展和延长其价值链，由此产生了再制造服务[3]。供应商是再制造服务战略中不可忽视的主体之一，制造商的产品回收和再制造战略会对供应商的零部件供应产生重大影响[4]。在再制造服务集成和协同运作模式下，再制造服务供应商是完成再制造服务的直接参与者和主要实施者，其服务活动的完成质量直接决定整个再制造服务的质量，因此，供应商选择决策问题成为再制造服务的关键。

目前关于供应商选择方法与模型的研究成果有不少。Wang等[5]针对具有直觉语言信息的多准则群决策问题，定义了新的分数函数与精度函数，并给出比较两种直觉语言数的简单方法。Ng[6]以最大化供应商评分为目标，建立一个加权线性规划模型来解决供应商选择问题，但没有考虑决策者权重变化对模型的影响以及线性规划对数据准确性要求过高而与实际决策环境不符等问题，并且计算过程复杂、运算量大、耗时长。秦娟等[7]提出基于极大熵配置模型与Choquet积分的物流供应商选择群决策方法，该方法同时考虑了专家偏好关联和评估指标关联的作用。Wu等[8]将模糊多属性决策方法应用于供应商的优选。Liu[9]针对具有梯形模糊直觉信息且属性权重完全或部分未知的问题，建立新的模型和公式确定属性权重，通过计算理想方案与备选方案的距离来对供应商排序。

再制造服务过程中，废旧产品的数量、批次有随机性，质量、工艺路线有不确定性，因此对再制造服务供应商在生产柔性、技术能力、价格成本等方面应有更高要求，而决策过程中，评价信息不易获取，决策指标与决策环境更加复杂，如何提高数据的准确性、实用性和保证决策的有效性成为决策的关键。供应商选择应由采购、生产、物流等多个部门共同决定，并考虑影响各个服务环节的诸多因素，这实质上是一个多准则群决策的排序择优问题，选择妥协最优解往往更符合企业管理需求，而改进型多准则妥协解排序方法(VIKOR)能够有效处理混合数据并保持数据转换过程中的真实性，在多准则群决策问题上有较大优势。因此，本文针对再制造服务过程中的供应商选择问题，结合语言值和模糊数进行主观评价，并运用熵权法确定决策者权重[10-11]，建立一种基于VIKOR的再制造服务供应商决策模型，最后通过实证研究和敏感性分析来验证模型的可行性，以期为再制造服务供应商的选择提供新的思路。

1 再制造服务过程和供应商

1.1 再制造服务过程

再制造服务由众多相互关联的服务功能活动按照既定次序组合而成，服务对象不同，对应的服务活动及其组合方式也不同，对于同一服务活动，其服务供应商也可能不同。如针对废旧机床的拆解清洗服务，必须根据其零部件状况采取不同的清洗措施，对普通油垢或泥垢只需进行高温高压清洗服务，严重污染零部件则需要高效喷砂绿色清洗服务。所以，根据清洗服务具体目标，需匹配能力相当的服务供应商。

根据再制造服务的特点，本文构建一种以供应商匹配决策为主导的三阶段再制造服务过程模型，如图1所示。

(1)再制造服务准备阶段。首先进行废旧产品性能检测及可再制造性评估，并根据需求确定再制造服务活动方案。然后根据质量、成本要求匹配出每一个服务活动的最优供应商，确定供应商决策方案。

(2)再制造加工服务阶段。根据前一阶段的再制造服务活动方案和服务供应商决策方案，督促相关供应商完成再制造拆解、清洗、加工、装配等服务活动。

(3)再制造物流服务阶段。再制造物流服务供应商根据给定的服务活动要求，确定再制造产品物流方案，完成再制造产品的仓储、运输交付等服务活动。

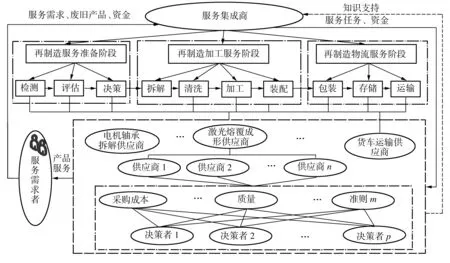
图1 再制造服务过程

1.2 再制造服务供应商

图1所示的再制造服务过程涉及服务需求者、服务集成商、服务供应商3个服务主体。服务需求者是再制造服务的起点与终点，即再制造服务起始于服务需求者向服务集成商发出需求，在完成一系列相关活动后，结束于服务集成者向服务需求者提供的再制造产品服务。服务集成商是再制造服务的组织者，它连接服务需求者和众多的服务供应商，按照服务需求者的要求安排相应的再制造服务功能活动，给出针对性的解决方案，并选择出合适的服务供应商。服务供应商是再制造服务的主要实施者，它为服务集成商在制定解决方案时提供知识支持，并根据服务集成者下达的相应任务，完成再制造服务过程的实际活动。再制造服务质量依赖于各供应商对服务活动的执行质量，因此再制造服务供应商的选择决策是整个再制造服务的关键。

2 再制造服务供应商的选择

2.1 供应商选择的决策方法

如前所述，供应商选择决策可描述为一个多准则群决策问题，即要将多个决策者对于方案的偏好按规则集结为决策群的一致/妥协偏好排序。对方案的评价通常包括定性和定量两种，其中定性评价如环境适应性、综合素质等通常采用自然语言，并采用模糊数进行定性指标的量化，部分定量评价指标由于受决策者素质和环境的影响，无法给出精确评分，也需要采用区间数、模糊数等形式进行表达。

VIKOR方法基于与理想解接近的折衷思想，通过最大化群体效益和最小化个别遗憾，对有限个决策方案进行折衷排序，得到决策者可接受的妥协解[12]，适用于准则间冲突或不可公度以及决策者无法准确描述偏好但能接受妥协方案的情况。

基于VIKOR的再制造服务供应商选择的决策步骤为：首先，采用数值、模糊数等多种数据类型描述评价信息，并进行规范化处理；然后，采用熵权法和信任函数对评价数据进行处理，得出相应的决策者和准则的权重；最后，用VIKOR方法择优排序，确定最优供应商。

2.2 评价信息及其规范化

2.2.1 数值型

原始评价数据uij规范化后记为rij,有

(1)

式中：i和j分别代表备选方案(即供应商)和评价准则；B为效应型准则集；C为成本型准则集。

2.2.2 直觉模糊数型

由于决策者的知识、经验、所处部门的不同或因时间限制，会导致评价信息具有不确定性。此外，复杂环境也会影响决策者的数值判断能力，使得决策参数的准确值难以获取，因此可采用直觉模糊数描述这些不确定的决策信息。

定义1 设X为一个非空集合，A={〈x,uA(x),vA(x)〉︱x∈X}为直觉模糊数集，其中uA(x)和vA(x)分别为元素x属于X的隶属度与非隶属度，uA(x),vA(x)∈[0,1]，且满足条件0≤uA(x)+vA(x)≤1。另外，定义πA(x)=1-uA(x)-vA(x)，表示元素x属于X的犹豫度，且0≤πA(x)≤1，称a=(uA,vA,πA)为直觉模糊数，也简记为a=(uA,vA)。

定义2 任意两个直觉模糊数a=(uA,vA,πA)和b=(uB,vB,πB)的距离为

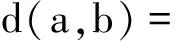
(2)

2.2.3 语言变量型

专家在决策评审过程中经常会给出文字评语，评语表达了专家的真实想法，成为评审的重要依据，将其转化为模糊数来处理，其评估标度和相应的直觉模糊数如表1所示。

表1 语言变量与直觉模糊数的转化

Table 1 Transformation of linguistic variables to intuitionistic fuzzy numbers

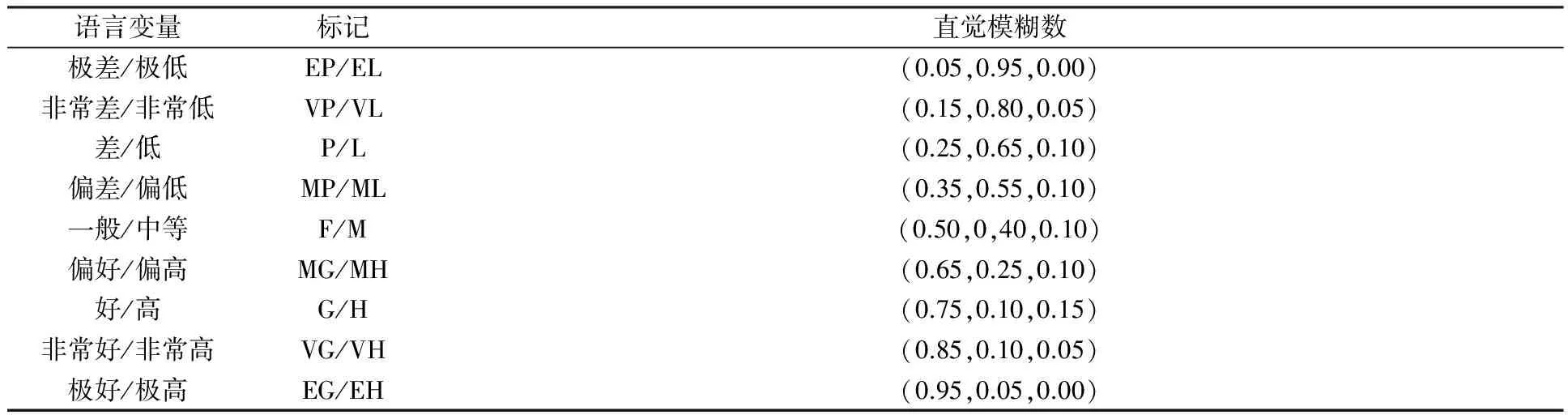
语言变量标记直觉模糊数极差/极低EP/EL(0．05，0．95，0．00)非常差/非常低VP/VL(0．15，0．80，0．05)差/低P/L(0．25，0．65，0．10)偏差/偏低MP/ML(0．35，0．55，0．10)一般/中等F/M(0．50，0，40，0．10)偏好/偏高MG/MH(0．65，0．25，0．10)好/高G/H(0．75，0．10，0．15)非常好/非常高VG/VH(0．85，0．10，0．05)极好/极高EG/EH(0．95，0．05，0．00)

2.2.4 区间数型

对于决策过程中的价格等不确定的评价指标，通常采用区间数来描述，其测度距离定义如下。

定义3 两个区间数α=[αL,αU]与β=[βL,βU]的测度距离为

(3)

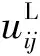
(4)

(5)

2.3 决策者和准则的权重

2.3.1 决策者权重

事情过去两天后，项目部副经理开始找我谈话。主题是我在这件事情上欠考虑，影响了正常的生产工作。我脑子热的已经冷静不下来了，心里倍感委屈，觉得自己并未做错什么，冷冷地甩下两句话：“我履行了自己的职责，处罚通报也是经你们同意的，如果你不满意我的工作，可以换人。”随后夺门而出。接下来的几天时间里，我完全没有工作的心，每天就在办公室做做资料，浏览一下网页，再也没去现场。

决策者对方案评价的不确定程度直接影响最终方案的排序，不确定程度越大则客观权重应越小。根据信息熵原理来确定决策者客观权重，定义信任函数为Bs(π)，决策者客观权重为λs，有

(6)

(7)

利用所得权重，根据层次分析法对主观评价信息集结，然后与客观评价信息加权组合得到综合评价矩阵R。

2.3.2 准则权重

对各评价准则采用语言变量进行评价，转化为直觉模糊数，并参照式(6)和式(7)先求出决策者权重，然后对准则主观评价值加权求和得到一阶矩阵T，在决策者对准则的语言评价中选取一个最优评价值，将其转化成直觉模糊数amax。对一阶矩阵T运用熵权法得到各评价准则的权重ωj为

(8)

其中

(9)

式(9)中：tj为T中的元素；d(tj,amax)参照式(2)计算。

2.4 基于VIKOR方法的排序择优

根据供应商评价决策矩阵对供应商进行择优，具体如下：

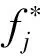
(10)

(11)

(12)

(13)

(14)

式中：S*=maxSi，S-=minSi；R*=minRi，R-=maxRi；v∈[0,1]为决策机制系数，v>0.5表示依据最大化群体效用机制进行决策，v<0.5表示依据最小化个体遗憾机制进行决策，v=0.5表示依据经协商达成共识机制进行决策。

步骤3 确定折衷方案。根据Si、Ri和Qi对备选方案进行排序，数值越小表示方案越优。

如果按照Qi值递增的方案排序为A(1)、A(2)、…、A(j)、…、A(n)，即A(1)为最优方案，且同时满足：①QA(2)-QA(1)≥1/(n-1)，其中n为备选方案总数；②方案A(1)依据Si、Ri排序也是最优方案，则判定A(1)为稳定的最优方案。若上述条件不能同时成立，则得到妥协解方案，这里又分为两种情况：

(1)若条件①满足而条件②不满足，则妥协解方案有2个：A(1)、A(2)；

(2)若条件①不满足而条件②满足，则妥协解方案有j个：A(1)、A(2)、…、A(j)，其中，j是根据QA(j)-QA(1)<1/(n-1)确定的最大化j值。

3 案例分析

3.1 问题描述及评价数据

目前我国各类热、冷轧辊和支承辊的年报废量达到140多万吨，对废旧轧辊的再制造利用具有良好的经济效益。本文以某轧钢厂废旧轧辊再制造服务中的表面处理环节为例，进行激光表面熔覆服务供应商的选择决策。

再制造服务平台中对应有4个潜在供应商(A1,A2,A3,A4)，选取最常用的8个供应商评价准则(C1,C2,…,C8)如表2所示，其中，C3和C4为成本型准则，其余为效应型准则，C1～C4为客观性指标，C5～C8为主观性指标。

表2 供应商评价准则

由采购、制造、质检3个部门组成的决策小组(D1,D2,D3)对4个潜在供应商进行评价，同时完成对所选8个评价准则的评价。经调研得到各供应商的客观性指标的原始数据如表3所示；决策者对各供应商的主观评价值如表4所示；决策者对各准则的主观评价值如表5所示，表中评价值表示相应准则的重要程度。

表3 供应商的客观指标值

表4 供应商的主观评价值

表5 评价准则的主观评价值

Table 5 Subjective evaluation values for the evaluation criteria

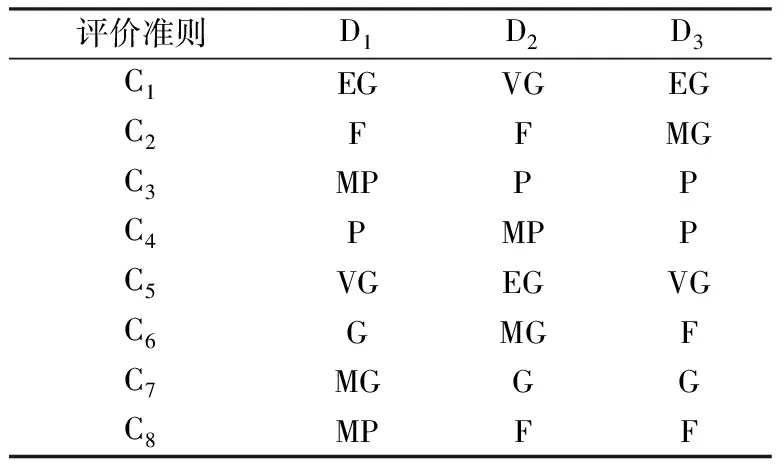
评价准则D1D2D3C1EGVGEGC2FFMGC3MPPPC4PMPPC5VGEGVGC6GMGFC7MGGGC8MPFF

3.2 基于VIKOR方法的供应商选择

首先，对表3的客观指标值按式(1)、式(4)、式(5)进行规范化处理。然后，利用表1将语言变量转化为直觉模糊数，列出主观评价值的π值矩阵，并利用式(6)求出B1(π)=-0.353、B2(π)=-0.366、B3(π)=-0.356，则决策者的权重分别为λ1=0.328、λ2=0.341、λ3=0.331。

根据求出的决策者权重，运用层次分析法对主观评价信息集结后，与规范化后的客观评价信息组合得到综合评价矩阵，见表6。

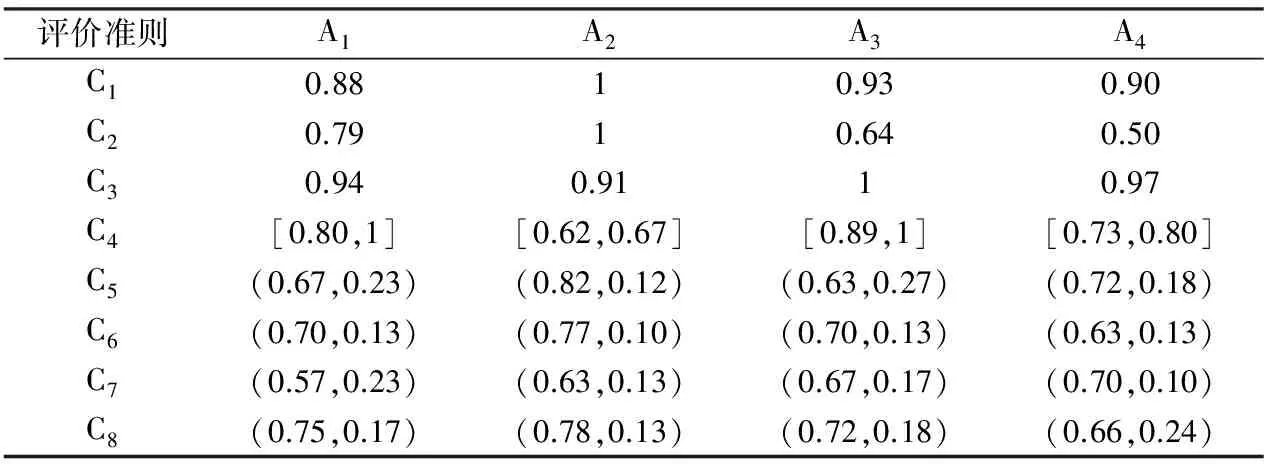
表6 综合评价矩阵

将表5转化成直觉模糊数矩阵，根据决策者权重将准则评价信息加权求和得到一阶矩阵T，选取表5中最优评价EG为amax=(0.95,0.05)，再由式(8)、式(9)计算出相应的准则权重如表7所示。

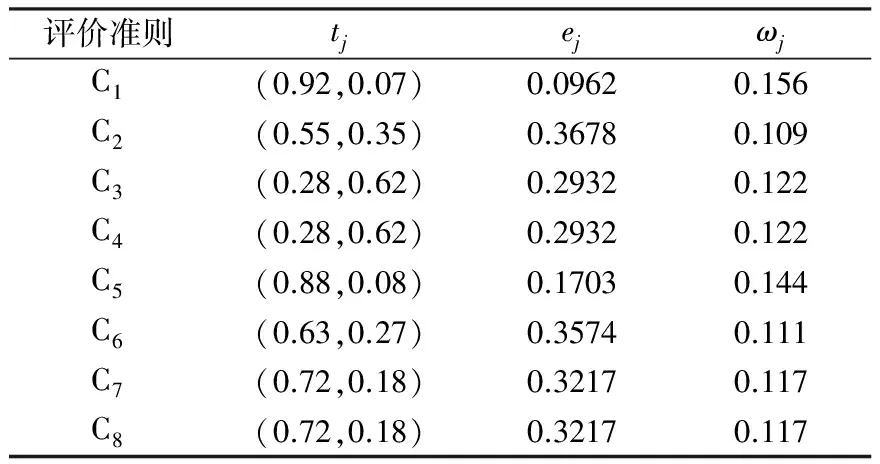
表7 评价准则的权重值

根据式(10)和式(11)可得表6中的最优值和最差值为：

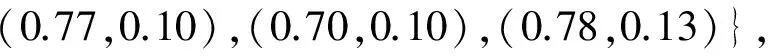
结合式(2)～式(3)与式(12)～式(14)，并取v=0.5，分别计算VIKOR排序值S、R和Q，结果见表8。

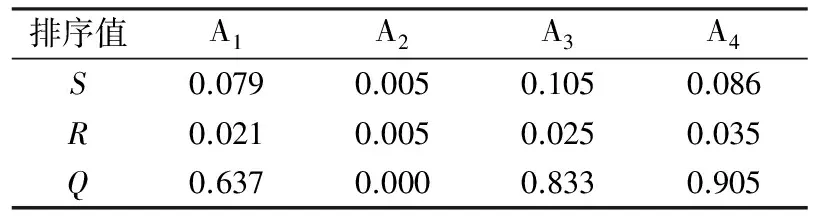
表8 各供应商的VIKOR排序值

根据S、R和Q的大小得到的方案优劣顺序分别为：A2>A1>A4>A3，A2>A1>A3>A4，A2>A1>A3>A4。几个排序中A2均为最优方案，且依照判定形式有QA1-QA2=0.637≥1/(4-1)，满足前述两个判定条件，因此可以认为供应商A2是该决策模型下的最优供应商。

3.3 结果对比分析

为了对比分析，本文还通过常用的决策方法AHP(层次分析法)与TOPSIS(逼近理想解排序法)对该实例进行了求解。由AHP法得出各供应商的评分为(0.9772,0.0071,1.3400,1.1106)，由TOPSIS方法得出各供应商的贴近度为(0.0462,0.1182,0.0566,0.0358)。3种方法的决策结果如表9所示。

表9 采用不同方法的决策结果对比

Table 9 Comparison of decision results by different methods

决策方法方案排序(优→劣)VIKORA2A1A3A4TOPSISA2A3A1A4AHPA2A1A4A3

3.4 敏感性分析

本文提出的基于VIKOR的供应商决策模型是通过主观评价方法确定准则权重。下面通过敏感性分析，研究在准则权重发生变化的条件下，供应商的优先排序是否会产生变化以及怎样变化。

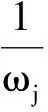
由图2可见，供应商A2的S、R值在32次实验中均为最小，即依此排序时A2为最优供应商，而在Q值排序中A2在第5、6、13、14、27、28次(约占18%)实验中不如其他供应商，即对应在准则C2(生产柔性)、C4(采购成本)、C7(技术支持)上的优劣排序是是不稳定的，这与对应准则权重的 变化相关｡从VIKOR 排序值的总体变化来看, 供应商A3与A4在大多数情况下都是排在后两位， A1则基本维持在第二的位置，这与准则权重扰动前的排序是一致的。综上，本文决策方法对准则权重的改变相对不敏感，即主观给定的准则权重值对决策结果影响很小，说明该模型的客观性和稳定性较好。

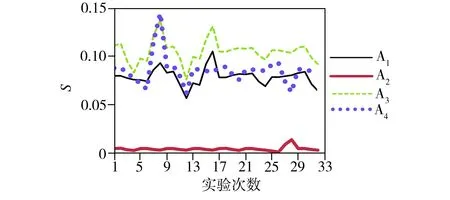
(a)S值

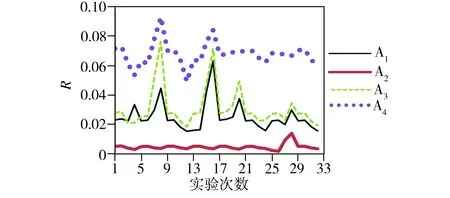
(b)R值

(c)Q值

Fig.2 Sensitivity analysis of VIKOR ranking values of the suppliers

4 结语

再制造服务供应商选择决策可转化为一个多准则群决策模型，针对一些常用决策方法的不足以及决策者和准则的权重设置具有主观性和不确定性的问题，本文提出了一种基于混合型VIKOR的供应商决策方法。首先构建了以服务需求者、服务集成商、服务供应商为服务主体，以供应商匹配决策为主导的三阶段再制造服务过程模型。然后引用定量准则下的数值型、区间数型和定性准则下的模糊数型、语言变量型等多种数据类型来描述评价信息，同时使用熵权法和信任函数求得各决策者和评价准则的权重，避免了主观赋权带来的二次不确定性。最后通过案例和敏感性分析验证了所建模型的可行性与稳定性。

[1] 徐滨士，董世运，史佩京.中国特色的再制造零件质量保证技术体系现状及展望[J].机械工程学报，2013，49(20):84-90.

[2] 徐滨士，董世运，朱胜，等.再制造成形技术发展及展望[J].机械工程学报，2012，48(15):96-105.

[3] 王蕾，夏绪辉，熊颖清，等. 再制造服务资源模块化方法及应用[J].计算机集成制造系统，2016，22(9):2204-2216.

[4] 丁斌，马海庆.两级再制造的S-M闭环供应链的决策与绩效分析[J].中国管理科学，2015，23(6):118-125.

[5] Wang X F, Wang J Q, Yang W E. Multi-criteria group decision making method based on intuitionistic linguistic aggregation operators[J]. Journal of Intelligent and Fuzzy Systems: Applications in Engineering and Technology, 2014,26(1):115-125.

[6] Ng Wan-Lung. An efficient and simple model for multiple criteria supplier selection problem[J].European Journal of Operational Research, 2008,186(3):1059-1067.

[7] 秦娟，李延来，陈振颂.基于极大熵配置模型与Choquet积分的物流供应商选择群决策方法[J].计算机集成制造系统，2015，21(10):2746-2759.

[8] Wu W Y, Lin C T, Kung J Y. Supplier selection in supply chain management by using fuzzy multiple-attribute decision-making method[J]. Journal of Intelligent and Fuzzy Systems: Applications in Engineering and Technology, 2013,24(1):175-183.

[9] Liu A F. Topsis method for multiple attribute decision making under trapezoidal intuitionistic fuzzy environment[J]. Journal of Intelligent and Fuzzy Systems: Applications in Engineering and Technology, 2014,26(5):2403-2409.

[10]Gülçin Büyüközkan. An integrated fuzzy multi-criteria group decision-making approach for green supplier evaluation[J]. International Journal of Production Research, 2012,50:2892-2909.

[11]Shemshadi A, Shirazi H, Toreihi M, et al. A fuzzy VIKOR method for supplier selection based on entropy measure for objective weighting[J]. Expert Systems with Applications, 2011,38(10): 12160-12167.

[12]Zhang N, Wei G W. Extension of VIKOR method for decision making problem based on hesitant fuzzy set[J]. Applied Mathematical Modeling, 2013,37(7):4938-4947.

[责任编辑 尚 晶]

VIKOR-based decision-making method for remanufacturing service supplier selection

XiaXuhui,HuJunfeng,WangLei

(Hubei Key Laboratory of Mechanical Transmission and Manufacturing Engineering,fWuhan University of Science and Technology, Wuhan 430081, China)

Remanufacturing service is one of the most important operation management modes to realize product multi-lifecycle. This paper builds a supplier matching decision-making oriented three-stage remanufacturing service process model for the remanufacturing service activities and their combinations. Since evaluation information of the vendors is complex and difficult to quantify, in order to keep its authenticity and practicality, a variety of data types such as interval number, linguistic variable and fuzzy number are used to describe this information. In view of the two types of evaluation criteria including objective and subjective ones and the evaluation information with mixed data types, VIKOR method is used to rank and select the alternatives. Thus the incommensurability of mixed data and the distortion in data conversion are solved, and the compromised optimal solution is more suitable for the actual requirements of the enterprises. To avoid the second uncertainty of subjective weight assignment, belief function and entropy weight method are applied to determine the weights of each decision maker and criterion. Finally, the feasibility and stability of the proposed method for supplier selection are verified by numerical example and sensitivity analysis.

remanufacturing service; supplier selection; VIKOR method; multi-criteria group decision-making; fuzzy number; entropy weight method

2017-03-13

国家自然科学基金资助项目(71471143)；武汉科技大学冶金矿产资源高效利用与造块湖北省重点实验室开放基金资助项目(2016zy013).

夏绪辉(1966-)，男，武汉科技大学教授，博士生导师.E-mail:xiaxuhui@wust.edu.cn

10.3969/j.issn.1674-3644.2017.04.011

C934

A

1674-3644(2017)04-0295-07