最小对称κ熵鞅测度和不完全市场中的定价问题

夏鹏程

(武汉大学数学与统计学院, 湖北 武汉，430000)



最小对称κ熵鞅测度和不完全市场中的定价问题

夏鹏程

(武汉大学数学与统计学院, 湖北 武汉，430000)

在等价鞅测度Me≠∅前提下,首先给出最小对称κ熵鞅测度的定义；其次给出最小对称κ熵鞅测度存在的充分条件，进而再给出最小对称κ熵鞅测度的密度表示(Radon-Nikodym导数)；最后讨论最小对称κ熵鞅测度的存在性和不完全市场的效用函数最大化是等价的.

κ熵鞅测度; 效用函数; 不完全市场

0 引言

在实际金融市场环境中，不完全市场占据很大的比例.但在不完全市场中，完全的套期保值是不可能的.不同的等价鞅测度，对应的无套利价格是一个区间[1-2].对于不同的等价鞅测度，人们也给出了一些准则[3-6],例如；q最优化鞅测度，最小方差鞅测度，最小熵鞅测度.

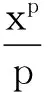
1 最小对称κ熵鞅测度

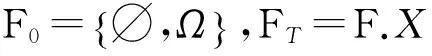
(1)

注 本文中总是假定Me≠∅.

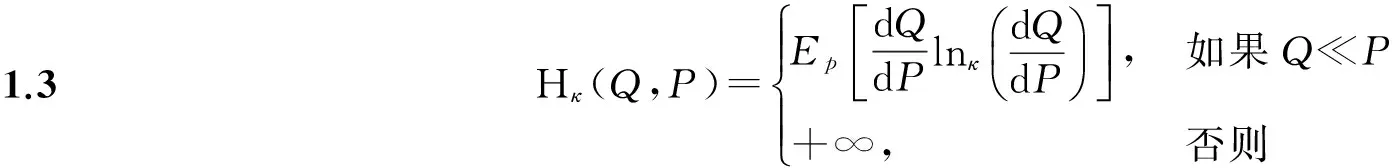
(2)

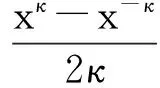
如果存在概率测度Q0∈M,满足Hκ(Q0,P)=minQ∈MHκ(Q,P), 则称Q0是最小κ熵鞅测度.

如果存在概率测度Q0∈Me,满足Sκ(Q0,P)=infQ∈MeSκ(Q,P), 则称概率测度Q0为最小对称κ熵鞅测度.特别地,当κ=1时，称Q0是最小方差对称鞅测度.当κ=0时，称Q0是最小对称熵鞅测度.

因为

(3)

为了方便，令

ψ(x)=(x-1)lnκ(x),x∈(0,+∞),
ψ′(x)=lnκ(x)+(x-1)lnκ(x),x∈(0,+∞),
ψ″(x)=2lnκ(x)+(x-1)lnκ(x),x∈(0,+∞)

(4)

则

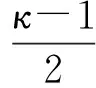
(5)

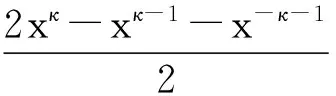
令

并且等式成立的充要条件是Q=P.

定理1.1的证明 如果存在性得证，由ψ(x)是严格凸的，易知唯一性也是成立的.

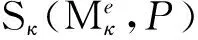
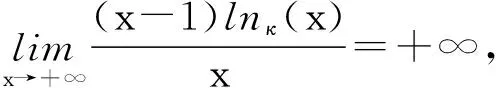
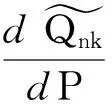
下面论证：Q0就是我们所要找的最小对称κ熵鞅测度.

由于X是有界的，不妨设存在常数C，使得X≤C, 对于∀ε>0,存在N，当n>N时，有

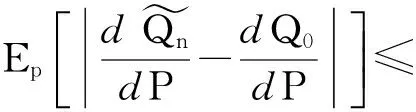
对上述的ε和N我们有

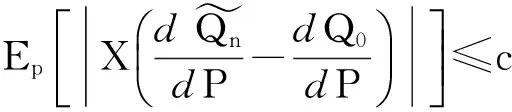
这就证明了

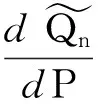
利用反证法：假设Q0并不是最小对称κ熵鞅测度.

假设

(6)

得到矛盾，故原假设不成立.

注意到:expκ(x)=exp-κ(x) , lnκ(x)=ln-κ(x). 因此在下面的讨论中我们只需要考虑0≤κ≤1.

证明1.1的证明

(7)

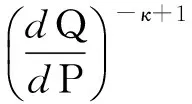
(8)

其中φ(x)=xlnκ(x).

引理1.2的证明 因为

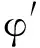
(9)

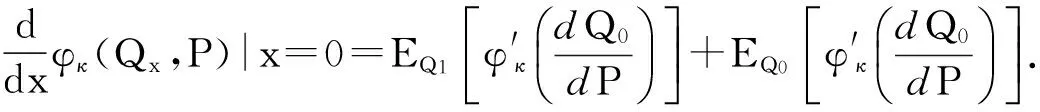
因为lnκ(x)是凸函数, 故

(10)

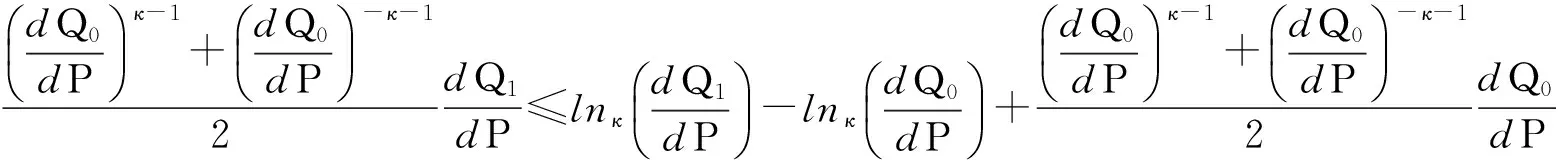
(11)

有引理1.1可知不等式的左边是可积的.

综上所述：

(12)

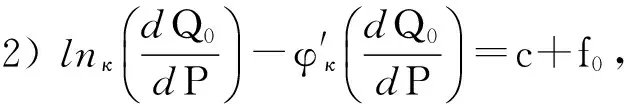
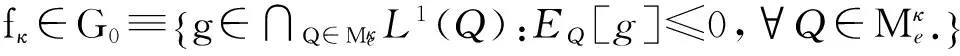
定理1.2的证明 必要性：

取

那么1)，2)式成立.

现在验证结论3)也是成立的.

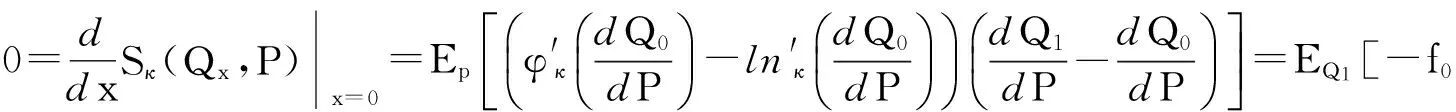
故EQ1[f0]≤0.

充分性：

-c-EQ1[f0]+c+EQ0[f0]=-EQ1[f0]

(13)

由条件3)知

Sκ(Q1,P)-Sκ(Q0,P)≥0.

这就说明了:Q0是最小对称κ熵鞅测度.

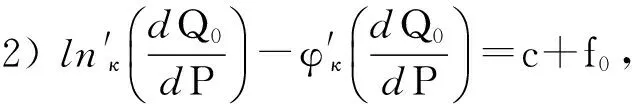
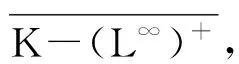
引理1.3证明 参考文献[5]中的定理，下面简单地叙述此定理，不给出详细的证明.

设(Ω,F,P)是一概率空间，G是L1(P)中的一凸集，且0∈E.则下面两个条件等价：

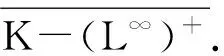
2) 存在η∈L∞,使得η>0,a.s,且supξ∈GE[ηξ]<∞.

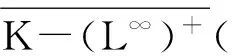
那么有上述的参考定理知：条件2)也成立，即存在η∈L∞,使得η>0,a.s, 且supξ∈KE[ηξ]<∞.

注意到:K是线性空间，因此supξ∈KE[ηξ]<∞等价于E[ηξ]=0,(∀ξ∈K).

b) 由引理可知：存在η∈(L∞)+,使得E[ηξ]=0,∀ξ∈K.

令

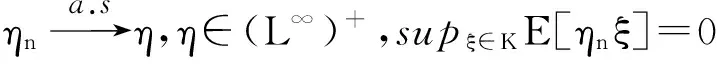
由于K是关于弱拓扑的一致可积族，则limn→+∞supξ∈KE[(ηn-η)ξ]=0.

那么由supξ∈KE[ηnξ]-supξ∈KE[ηξ]≤supξ∈KE[(ηn-η)ξ] 可知： 存在充分大的m0,使得supξ∈KE[ηm0ξ]≤+∞，即,E[ηm0ξ]=0,∀ξ∈K.

又因为|ηnf0|≤|ηf0|,而不等式的左边是可积的. 利用控制收敛定理可得: 存在充分大的m1,使得EQ[ηm1]>0.

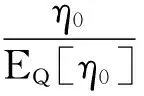
由EQ1[f]=0,知Q1∈Me.

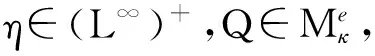
(14)

由于-lnκ(x)是单调递减的函数， 故：

(15)

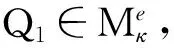
1) 如果gκ∈K,Q是最小对称κ熵鞅测度.

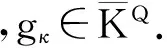
2 最小对称κ熵鞅测度的金融解释

考虑具有实际背景的金融市场，一般投资组合的最优化取决于效用函数期望的最大化.从这个角度出发，考虑最小对称κ熵鞅测度和投资组合最优化之间的联系.

定义2.1 设μ是R→R的函数，并且满足

1)μ是二次可微的，

2)μ是单调递增的凹函数，

3) limn→+∞=0，

则称μ是效用函数.

考虑实际的金融背景，因此我们只考虑满足Ep[|VT(φ)|]≤+∞的所有投资组合φ,满足这样的φ的全体记为G.

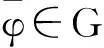
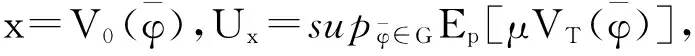
现在考虑最小对称κ熵鞅测度.

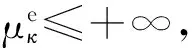
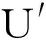
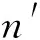
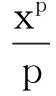
μ1(x)=exp(-x-1),μ2(x)=xp-1.

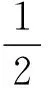
从图1(a)中可知:当x值越来越大时,y+xy+ylny=1和y-x-0.5=0越来越接近.这就说明了我们给出的最小κ熵鞅测度更加贴近实际的金融市场.

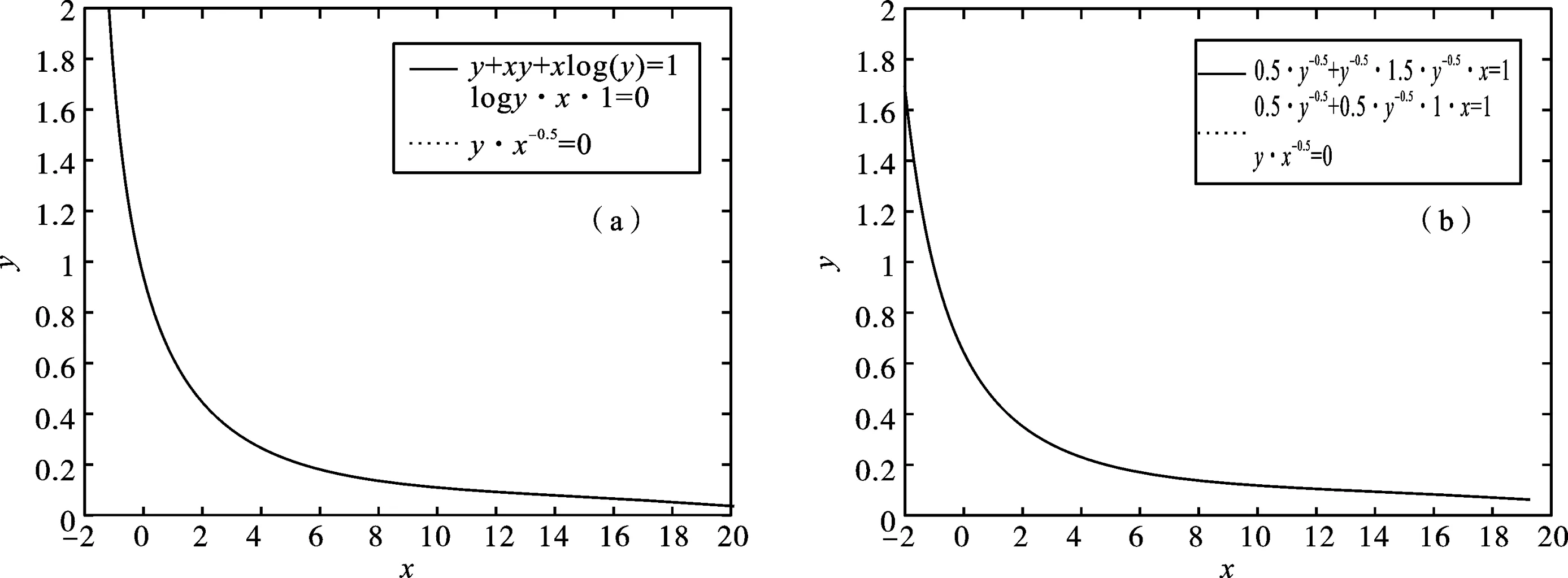
图1 不同k值曲线变化图

从图1(a)中可知:我们选取不同的κ进行比较，κ分别取：κ=0,κ=-0.5,κ=-0.25,κ=0,κ=0.25(注意；这条曲线没有在图像中显示出来，这是因为它和κ=0.25重合了.),κ=0.5进行比较，当x越来越大时，并不是κ=0时，它和实际的金融市场是最贴近的. 图2是取不同的κ值(分别取:κ=0,κ=0.5,κ=-0.5)和最小κ熵鞅测度进行的比较.图像中的3条曲线分别是取值为κ的最小κ熵鞅测度对应的效用函数，取值为κ最小对称κ熵鞅测度所对应的效用函数和取值q=0.5的,效用函数形式为μ(x)=xpp,从图中可以看到对于不同的κ而言，最小对称κ熵鞅测度对应的效用函数比最小κ熵鞅测度对应的效用函数更加贴近于取值q=0.5 的,效用函数形式为μ(x)=xpp，也就是说最小对称κ熵鞅测度在特定场合定价将优于最小κ熵鞅测度.

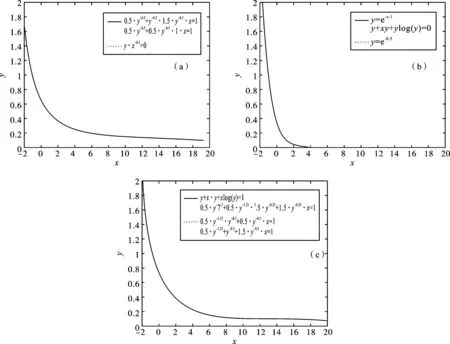
图2 不同κ值与最小熵鞅测度比较a) κ=0；b) κ=0.5；

3 参考文献

[1] Frittelli M.The minimal entropy martingale measure and the evaluation problem in incomplete markets[J].Math Finance,2000,10(1):39-52.

[2] Schachermayer M.A counterexample to several problems in the theory of asset pricing[J].Math Finance,1993,3(2):217-229.

[3] Barbara Trivellato,The minimal κ entropy martingale measure[J].World Scientific,2012,15(5):1-23.

[4] Grandits P and Rnlander T.On the minimal entropy martingale measure[J].Ann Prob 2012,30(2):1003-1038.

[5] 严加安.测度论讲义[M].北京:科学出版社，2004:222-224.

[6] Pistone G.κ-exponential models from the geometrical viewpoint[J].Eur.Phys,2009,70(2):29-37.

[7] 汤思英，刘继春，杜丽金.最小对称熵鞅测度和不完全市场的定价问题[J].厦门大学学报,2004,43(4):1-4.

[8] 王江.金融经济学[M].北京:中国人民大学,2006:87-98.

(责任编辑 赵燕)

The minimal symmetrickentopy martingale measure and valuation problem incomplete market

XIA Pengcheng

(School of Mathematics and Statistics,Wuhan University,Wuhan 430000,China)

Under the assumption that the setMe≠∅ of equivalent martingale measures ,the concept of the minimal symmetricκentropy martingale was brought out , we find a sufficient condition for the existence of a unique equivalent martingale measure that minimizes the symmetricκentropy ,moreover the characterization of the density of the minimal symmetricκentropy martingale measure was provided.Finally we discuss the relationship between the minimization symmetricκentropy and the maximization of the utility function.

κentropy martingale measure; utility function;incomplete market

2016-06-30

夏鹏程(1991-), 男，硕士生， E-mail:2014202010052@whu.edu.cn

1000-2375(2017)04-0429-08

文献标志码：A DOI：10.3969/j.issn.1000-2375.2017.04.017