对奇异p(x)-Laplace方程正解存在性定理的应用

张晓丽

（赤峰学院 数学与统计学院，内蒙古 赤峰 024000）

对奇异p(x)-Laplace方程正解存在性定理的应用

张晓丽

（赤峰学院 数学与统计学院，内蒙古 赤峰 024000）

本文应用文献[1]中的主要结果,即p(x)-Laplace方程正解的存在性定理给出了一些结论及证明.

解的存在性；p(x)-Laplace算子；上下解

1 预备知识

定理 1.1[1]如果(A1)和(A3)成立，问题（1）在空间W1,p(x)

（ⅰ）(A2)成立并且

或

（ⅱ）(A4)成立，

则问题（1）存在一个位于有序区间[u,u]中的解.

其中的问题(1)是如下的奇异p(x)-Laplace方程Dirichlet问题

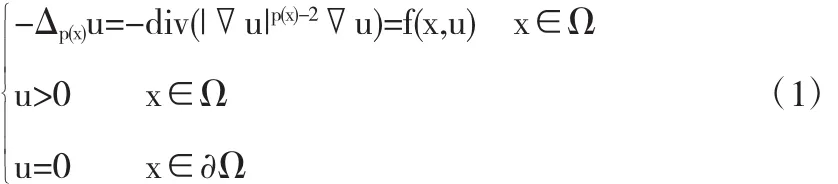
这里Ω是RN上的一有界C2域，N≥3，p算子 Δp(x)u=-div(|▽u|p(x)-2▽u)是所谓的p(x)-Laplace算子，f是Ω×(0, +∞)上的Caratheodory函数，满足

(A1)a0(x)≤f(x,t)≤a1(x)t-γ(x),(x,t)∈Ω×(0,t0),这里a0(x)，a1(x)是可测函数，并且a1(x)≥a0(x)>0，γ(x)>0，t0>0，γ(x)∈C(Ω).

注 满足上述条件的f(x,t)在t=0点可能出现奇性.

除上述两个条件外，本文主要结果还用到假设(A3)存在一属于的非负函数φ满足其中r(x)＜p*(x)，并且代表一个一般的正常数.

定理1.2[2]如果f满足条件这里则泛函Φ在W01,p(x)(Ω)存在全局最小值u，并且u是问题的弱解.

定义1.3[3]u∈W01,p(x)(Ω)称为问题(2.1.1)的下解(resp.上解)，如果u满足

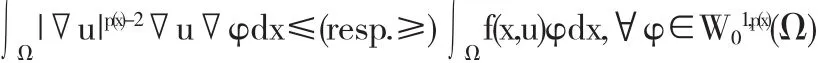
2 本文的主要结论及证明

定理2.1 如果条件 (A1),(A2),(A3)成立,并且存在一个t1>t0，使得f(x,t1)≤0,x∈Ω.则（1）存在一个解小于等于t1.

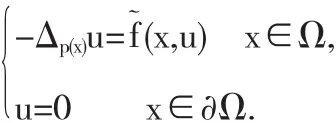
存在一个解t1.

由于

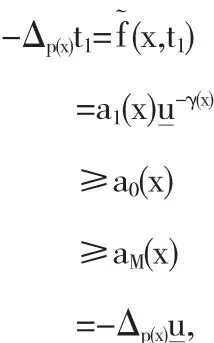
所以有t1≥u.

故由上式和条件(A1),f(x,t1)≤0,可以得到如下的不等式

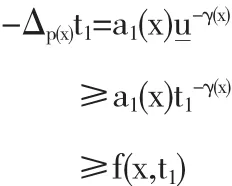
所以t1是问题（1）的一个上解,并且t1∈L∞(Ω).又条件(A1),(A2),(A3)成立,所以依据定理1.1可以得到问题（1）的一个解u≤t1.

定理2.2 如果条件(A1),(A2),(A3)成立,并且

其中B为常数,1≤β＜p-，则问题（1）存在一个解.

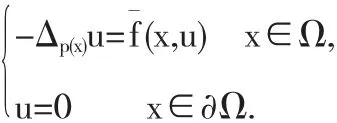
存在一个解u由于

故由上式和条件(A1)，(2)可以得到如下的不等式

记这就是p(x)-Laplace方程的第一特征值.我们知道，如果p(x)恒等于常数p,则第一特征值为正，并且第一特征值为正对于研究p-Laplace问题是十分重要的，然而对于一般的函数p(x)，第一特征值一般是等于0的.只有在极为特殊的情况下，第一特征值为正.在以下的讨论中我们假设：存在一个向量l∈RN{0}使得对于任意的x∈Ω，f(t)=p(x+tl)对t∈Ix={t|x+tl∈Ω}是单调的.

定理2.3 如果条件(A1),(A2),(A3)成立，并且

对某一个0≤λ＜λ1成立，则问题（1）存在一个解.

证明 设

则有如下不等式成立

所以有下面的不等式成立

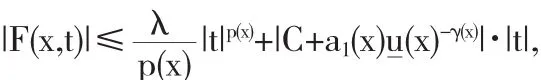
因为

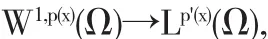
即存在一个常数C满足

所以

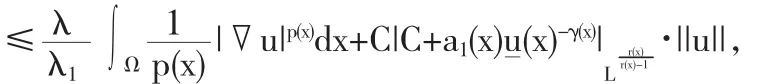
所以

因为λ＜λ1,p->1，所以当||u||→∞时,Φ(u)→∞又由于Φ是弱下半连续的,所以泛函Φ在空间W01,p(x)(Ω)存在全局最小值点即

存在解u.所以由条件(A1)可以得到如下的不等式

故依据上式,(3)式和条件(A1)有如下的不等式成立

面定理1.1可以得到问题(1)存在一个解.

定理2.4 如果条件(A1),(A2),(A3)成立，并且存在t1≥t0,使得

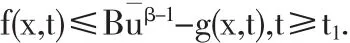
Caratheodory函数，满足

这里

并且在一个正测度集上有

成立，则问题（1）有一个解.

证明 取h∈C(T,[0,1])，使得当t≤t1时，h(t)=1；存在t2，使得当t≥t2>t1时，h(t)=0,并且令

只需证明具有

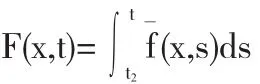
的泛函Φ是有下界的而且为强制的.

我们有当t≥t2时，所以有

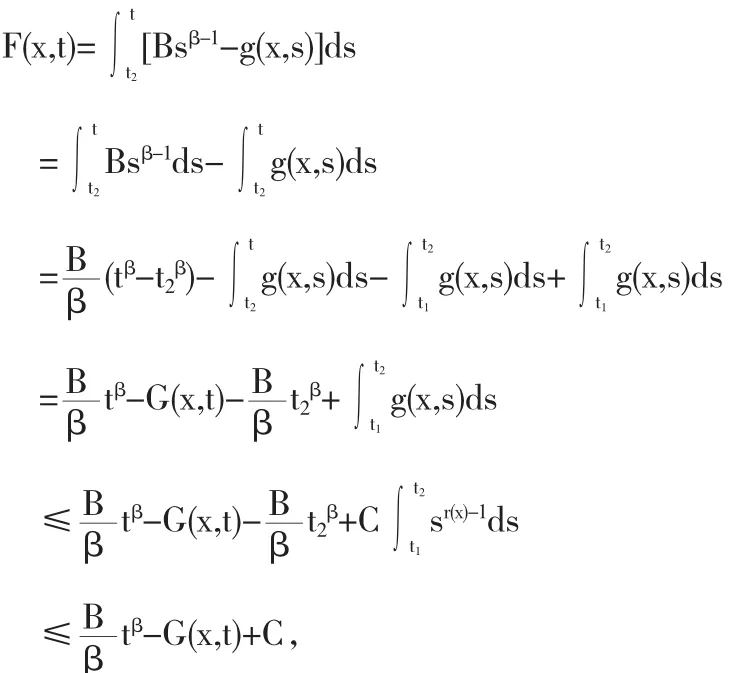
所以有如下的不等式成立

所以

所以依据(5)知Φ有下界.下证Φ是强制的.

假设Φ不是强制的，即

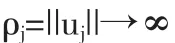
但

则子列

在W01,p(x)(Ω)中弱收敛于u˜.因为

则

所以依据(6)和Fatou's lemma有

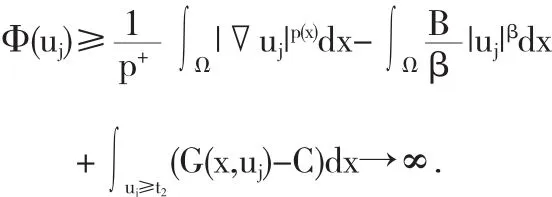
与假设矛盾，所以Φ是强制的.

〔1〕张晓丽.奇异p(x)-Laplace方程正解的存在性[J].赤峰学院学报(自然科学版),2014.

〔2〕Qingzeng song,Existence of Solutions for Singular Quasilinear Elliptic Equation[D].

〔3〕Fan,X.L,On the sub-supersolution method for p(x)-Laplacian equations,J.Math.Anal.Appl.(2006),doi:10.1016/j. jmaa.2006.07.093.

〔4〕郭大钧.非线性泛函分析(第二版)[M].山东：山东科学技术出版社，2001.

O175

A

1673-260X（2017）06-0010-03

2017-03-04