一元线性回归中自相关的处理
2017-07-06王淑超马永梅
王淑超,马永梅
(巢湖学院 应用数学学院,安徽 合肥 238000)
数理研究
一元线性回归中自相关的处理
王淑超1,马永梅2
(巢湖学院 应用数学学院,安徽 合肥 238000)
涉及时间序列的线性回归模型往往会出现自相关问题,以往学者在建模时大多忽略了自相关问题而直接使用普通最小二乘法进行回归,这会造成模型的估计不够准确.文章对自回归进行阐释,利用保险业数据实证分析自回归的检验方法和解决办法.广义差分法解决自回归问题使得线性回归模型的普通最小二乘估计量具有良好的统计特性.
线性回归;自相关;自相关检验;广义差分;财产保费
1 问题提出
回归分析是研究一个所谓的因变量对另一个或多个所谓自变量的依赖关系,并通过自变量在重复抽样中的已知或设定值,去估计或预测因变量的总体均值.根据回归模型中参数是否线性,回归分析可以分为线性回归分析和非线性回归分析.[1]
线性回归模型的一般形式为:

对线性回归模型进行估计常用的方法是普通最小二乘法,使用普通最小二乘法对线性回归模型进行估计时首先要进行如下假设:随机干扰项零均值、同方差、相互独立且服从正态分布,随机干扰项与自变量不相关,自变量之间不存在线性相关.满足以上假设的线性回归模型被称为经典线性回归模型,经典线性回归模型使用普通最小二乘法进行估计具有良好的统计特性.[1]
实际上,并不是所有的回归分析问题都能满足经典假设,在不满足经典假设时使用普通最小二乘法进行估计的结果就值得怀疑,结果可能并不可靠,尤其在时间序列数据中,常常会违背“随机干扰项相互独立”的假设,此时即存在自相关问题.
如果回归模型不满足“随机干扰项相互独立”的假设,则称为自相关.[1]
自相关按形式可以分为一阶自相关和高阶自相关.[1]若ui=ρui-1+vi(-1<ρ<1),则该模型存在一阶自相关;若ui=f(ui-1,ui-2,…)+vi,则存在高阶自相关.其中,ρ为自相关系数,vi为经典误差项.
回归模型存在自相关时使用普通最小二乘法对回归模型进行估计会导致估计的参数非有效、模型预测失效等问题.因此在对回归模型进行估计前,检验其是否存在自相关问题就尤为重要.
2 实证检验自相关及其eviews实现
近年来,随着人们收入水平的提高,人们对财产的风险控制意识增强,我国的财产保费收入迅速增长,因此可将衡量人们收入水平的国家GDP作为自变量X,将我国的财产保费总收入作为因变量Y,建立一元线性回归模型.[2]然而,财产保费总收入的时间序列除了受GDP影响外,可能受人们保险意识的影响自身具有一定的惯性,因此需要检验其是否存在自相关问题.文章采用1997-2015年我国GDP和我国财产保费总收入数据进行实证分析,数据来源于国家统计局网站.
建立一元线性回归模型(1):

使用普通最小二乘法进行估计,估计结果如式(2):
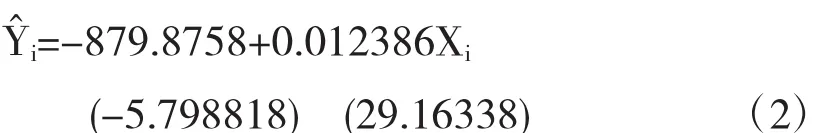
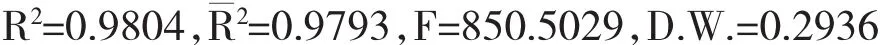
括号内的数字为回归系数对应的t统计量的值(下同),由回归结果可以看出,拟合系数为0.9804,说明模型拟合的较好;回归系数的t统计量的值较大,对应的p值接近于0,说明变量显著.
2.1 图示检验法
作残差和滞后一期残差的关系图,绘制图形如图1.由图1可以看出大多数散点落在第1、3象限内,说明残差之间存在正相关.
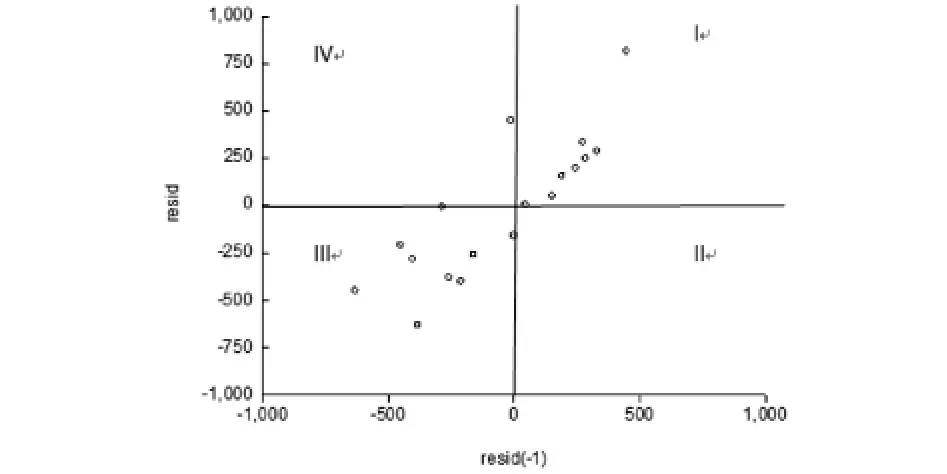
图1 即期残差与滞后残差
2.2 D.W.检验
检验自相关最常用的检验是德宾-沃森检验,简称为D.W.检验.其原理是利用线性回归的残差构造D.W.统计量,见式(3),并可根据显著性水平和样本容量查临界值的上限du和下限dL,根据D.W.统计量落在不同区间得出不同的结论,见图2.

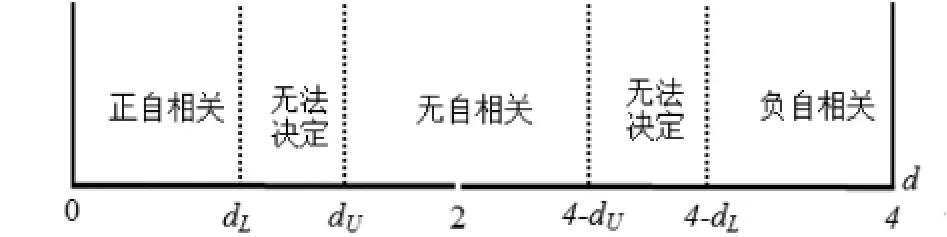
图2 D.W.统计量判别[1]
由回归结果(2)得D.W.=0.2936,数值较小,小于显著性水平5%和样本容量为19的临界值dL=1. 18,说明模型存在一阶自相关.但是D.W.检验只适用于存在一阶自相关的情形,对于高阶自相关无法检验,因此需要进一步使用其他方法进行检验.
2.3 LM检验
LM检验不仅可以检验模型是否存在自相关,还能检验模型存在自相关的阶数,它是通过建立残差项关于自变量和滞后期残差项的辅助回归模型完成的.在eviews软件的回归结果窗口中点击”View/Residual Tests/Serial Correlation LM Test”,将滞后期分别设为1、2,分别得到如式(4)、式(5)的估计结果:

由式(4)、式(5)的估计结果分析可得:在5%的显著性水平下,三个模型的拟合系数均较高,F统计量均显著,说明三个模型在整体上均是显著的;由模型中变量的t统计值可以看出,只有模型(4)中各变量均显著;由模型的LM值可以得出,模型存在自相关,结合模型中各变量t统计量的大小可以得出模型只存在一阶自相关,不存在高阶自相关.因此可利用式(2)中的D.W.计算的
2.4 回归检验法
回归检验法是对原模型式(1)进行回归,根据回归结果计算残差序列ei=yi-yˆi,然后对残差序列ei用普通最小二乘法进行不同形式的回归拟合,如式(6)、式(7):

由式(6)和式(7)的估计结果可知,两个模型的拟合系数均较大,说明两个模型整体拟合较好;由模型中t统计值可知,在1%的显著性水平下,模型(6)中变量显著,模型(7)中ei-2不显著,说明原模型(2)只存在一阶自相关,不存在高阶自相关.由模型(6)可知
回归检验法得到的ρ值原则上应该与利用式(2)中D.W.计算的ρ一致,文章中两者有差别的原因是:一方面回归检验由于采用滞后期导致自由度有所降低,另一方面是关系式是在样本容量充分大时成立,本文的样本容量并没有达到充分大.
3 自相关的解决方法
当模型存在自相关时,直接使用普通最小二乘法进行估计可能得到不正确的估计结果,因此须消除自相关,本文采用广义差分法消除自相关.广义差分法是将原模型转化为对应的差分形式以消除自相关,然后再通过普通最小二乘法对差分后的模型进行估计,从而间接得到原模型的估计值.
对式(1)取滞后一期后,两边同乘以ρ作变换Yt-ρYt-1,得到式(8):
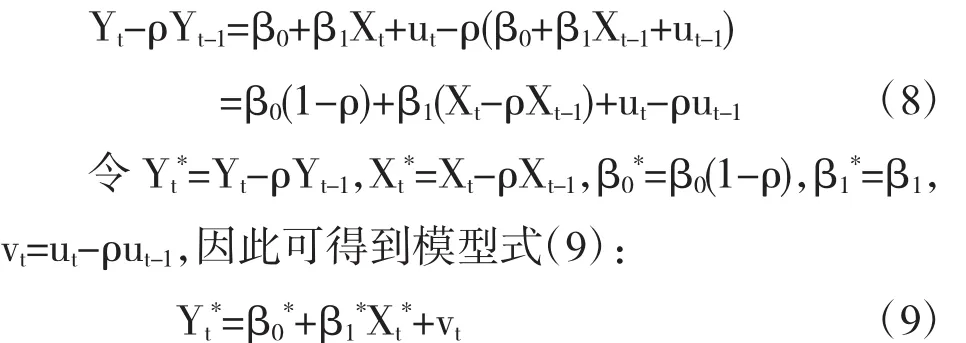
由于vt满足经典假设,新模型不存在自相关问题.本文采用回归检验法得到的ρˆ=0.8532对数据进行处理,用处理后的数据对式(9)进行回归得到式(10):

由式(10)的估计结果可知,在5%的显著性水平下,模型的拟合系数为0.925449,拟合优度较高,F统计量为198.6168,说明模型整体上显著;x的回归系数的t统计值较大,变量x显著;dL=1.18,dU=1. 40,dL≤D.W.=1.008553≤dU,因此无法使用D.W.值检验是否存在自相关,经过LM检验,式(10)不再存在自相关.根据差分模型的参数估计值计算原模型的参数估计值,如式(11)和式(12):

因此,消除自相关的回归模型为Yˆi,经济含义是我国财产保费收入的1.4171%是由我国GDP的增长引起的.
4 结论
在使用普通最小二乘法建立线性回归模型对时间序列数据进行分析时,首先要检验是否存在自相关问题,残差图、D.W.检验、LM检验、回归检验等都可以检验自相关问题.其中残差图的方法只适合初步判断是否存在自相关,无法给出精确的结果;D.W.检验只适合检验存在一阶自相关的情况不适合存在高阶自相关时使用;LM检验和回归检验是检验自相关问题比较好的方法,不仅可以检验自相关是否存在,还可以检验存在自相关的阶数.对存在自相关的模型可以采用广义差分法进行处理,然后再采用普通最小二乘法回归.
〔1〕张晓彤.计量经济学基础[M].4版.天津:南开大学出版社,2014:135-157.
〔2〕张芳洁.影响我国保险业发展的经济因素的实证分析[J].数量经济技术经济研究,2004,21(3): 25-31.
〔3〕刘明,王永瑜.Durbin-Watson自相关检验应用问题探讨 [J].数量经济技术经济研究,2014,31(6):153-160.
〔4〕林天水,陈佩树.一元线性回归中异方差的处理[J].统计与决策,2015,31(21):86-88.
O212
A
1673-260X(2017)06-0001-03
2017-03-11
安徽省重点科研项目(KJ2016A505);巢湖学院校级科研项目(XLY-201502)
