磁场中氦原子内电子的自旋效应研究

赵丽丽，师晓敏，赵翠兰

（1.赤峰学院 计算机与信息工程学院，内蒙古 赤峰 024000；2.内蒙古民族大学 物理与电子信息学院，内蒙古 通辽 028043）

数理与计算机

磁场中氦原子内电子的自旋效应研究

赵丽丽1，师晓敏2，赵翠兰2

（1.赤峰学院 计算机与信息工程学院，内蒙古 赤峰 024000；2.内蒙古民族大学 物理与电子信息学院，内蒙古 通辽 028043）

本文利用求解能量本征方程方法，研究外磁场对氦原子中两电子体系能量的影响，进而研究自旋效应.理论结果表明，若自旋状态在磁场方向的投影为零，则自旋磁矩与外磁场的相互作用能量为零，自旋对体系无影响；反之，若自旋状态在磁场方向的投影不为零，则自旋磁矩与外磁场的相互作用能量不为零，自旋对体系有影响.所以，氦原子处于基态时，自旋对体系无影响；处于激发态时，自旋的影响随自旋状态的不同而不同.

电子；能量；自旋；自旋磁矩；轨道磁矩

1 引言

量子力学是研究微观粒子运动规律以及相关现象的理论，由于微观粒子具有波粒二象性，导致其运动规律与经典力学有本质区别.其状态由波函数描述，状态变化遵从薛定谔方程.当势函数不显含时间时，薛定谔方程的求解归结为能量本征方程的求解.通过求解能量本征方程，可以获知体系的物理性质，如方势阱中的粒子、线性谐振子以及氢原子等体系的能量是量子化的、不同状态上粒子概率密度分布不同等.微观粒子除轨道运动外，还有自旋，自旋是一种相对论效应.具有相对论效应的微观粒子的运动服从狄拉克方程，该方程的哈密顿量在非相对论极限下会有一项与自旋相关的项，将其引入薛定谔方程，可以研究微观粒子的自旋.

本文主要研究磁场中氦原子内电子的自旋性质.为简单起见，将电子之间的相互作用忽略，将体系视为两电子理想体系.根据类氢体系构造系统的本征函数，求得能量本征值，进而研究自旋与磁场的关系.

2 理论推导

将氦原子至于外磁场 中,计及自旋后，两电子体系的哈密顿量为[1]

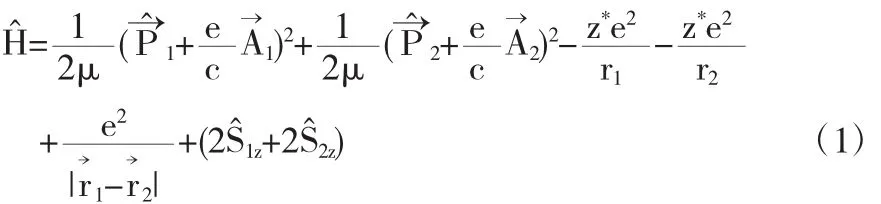
其中μ为电子质量，c为光速，z*是有效核电荷数.分别是电子1(2)相对于原子核的位置矢量、自旋角动量在 轴的投影、动量、矢量势.选取如下的矢量势

将（2）式代入（1）式，整理得

式（8）的解为[1]

2.1 基态性质

氦原子处于基态时，两个电子均处于1s态，其空间波函数为对称波函数

则两电子自旋波函数为反对称化波函数

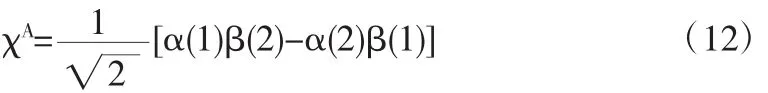
其中α(i)，β(i)，i=1,2是第i个电子自旋角动量Sz的本征态，满足

两电子体系的总波函数应为

2.2 第一激发态性质

两个电子一个处于n=1的态φ100，一个处于n=2的φ200，φ210，φ211，φ21-1.此时两电子体系的自旋波函数分别为

体系基态能量的期待值为

但空间波函数有几种不同情况，下面分别计算.

2.2.1 两个电子分别处于φ100或φ200态体系的空间波函数为

则体系的总波函数分别为经过计算，得

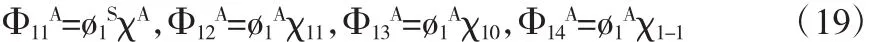
2.2.2 两个电子分别处于φ100或φ210态

体系的空间波函数为

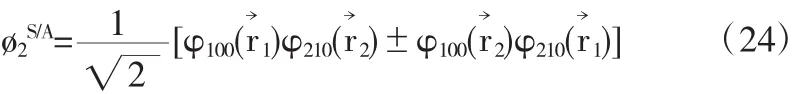
体系的总波函数分别为

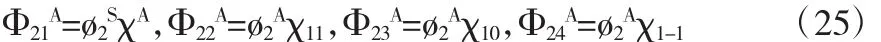
经过计算，得

2.2.3 两个电子分别处于φ100或φ211态体系的空间波函数为

体系的总波函数分别为

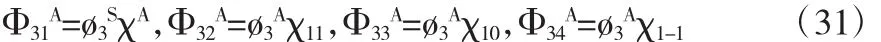
经过计算，得

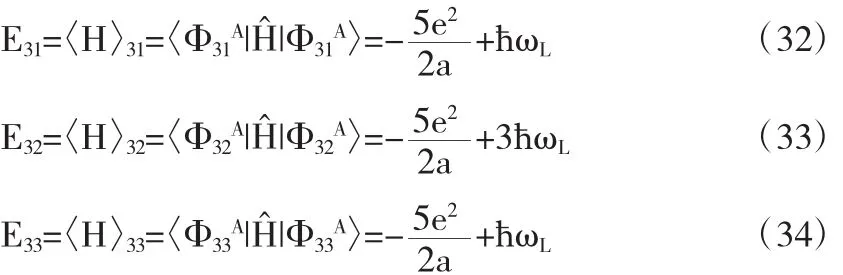
2.2.4 两个电子分别处于φ100和φ21-1态

体系的空间波函数为

体系的总波函数分别为

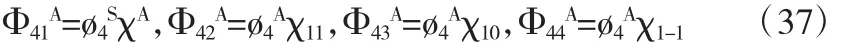
经过计算，得

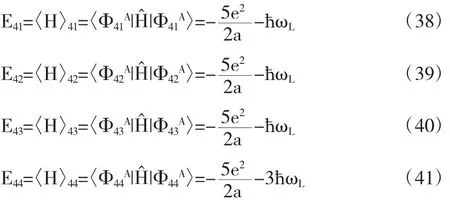
3 结果与讨论

从理论推导可知，当体系所处状态不同时，自旋运动、轨道运动磁矩对体系的影响不同.如果体系总波函数中含自旋波函数χA或χ10、含有空间波函数φnlm(m=0)，则由于〈χA|SiZ|χA〉=0或〈χ10|SiZ|χ10〉=0，及〈φnl0|lˆZ|φnl0〉=mħ=0，导致自旋磁矩与轨道磁矩对体系能量无贡献，则外磁场对体系能级无影响，如式（20）所示.

若体系总波函数中含有自旋波函数χ11和χ1-1，则自旋磁矩对能量有影响，在χ11态上，自旋对能量的影响为2ħωL；如式（21）、（27），在χ1-1态上，自旋对能量的影响为-2ħωL，如式（23）、（29）.

若体系中的空间波函数中含有φnlm(m≠0)，则轨道磁矩对能量有影响，在φ211态上，轨道运动对能量的影响为ħωL，如式（32），在φ21-1态上，轨道运动对能量的影响为-ħωL，如式（38）.

当体系所处状态含有χ11，χ1-1或χ211，χ21-1态时，自旋运动、轨道运动均对体系能量产生影响，如式（33），轨道运动的贡献为ħωL，自旋的贡献为2ħωL，其它的可以同样分析.所以，外磁场对体系是否产生影响，取决于体系所处的状态.若有影响，则能量正比于，即与外磁场成线性关系.

4 结论

利用求解能量本征方程方法，通过具体构造体系反对称化波函数，研究外磁场对体系能量的影响，进而研究氦原子中两电子体系的自旋效应.从理论结果看到，自旋是否对体系能量产生影响，取决于体系自旋磁矩与外磁场的相互作用.若体系波函数中含有自旋波函数χ10或χ00，自旋磁矩在外磁场方向的投影为零，则自旋对体系能量无影响，若体系波函数中含有自旋波函数χ11和χ1-1，自旋磁矩在外磁场方向的投影不为零，分别为，则自旋磁矩对能量有影响，在χ11态上，自旋对能量的影响为2ħωL，在χ1-1态上，自旋对能量的影响为-2ħωL；由于，则能量正比于，即能量随外磁场线性增加或线性减少.

〔1〕曾谨言.量子力学教程[M].北京：科学出版社，2014.

O413.2

A

1673-260X（2017）06-0001-02

2017-03-22