长江经济带工业环境效率差异及其影响因素——基于超效率DEA-Malmquist-Tobit模型

马 骏，王雪晴

(1.河海大学商学院，江苏南京 211100；2.南京大学理论经济学博士后流动站，江苏南京 210009；3.江苏省水资源与可持续发展研究中心，江苏南京 210098)



长江经济带工业环境效率差异及其影响因素
——基于超效率DEA-Malmquist-Tobit模型

马 骏1，2，3，王雪晴1，3

(1.河海大学商学院，江苏南京 211100；2.南京大学理论经济学博士后流动站，江苏南京 210009；3.江苏省水资源与可持续发展研究中心，江苏南京 210098)

以长江经济带11个省市为研究对象，运用超效率DEA模型对2005—2014年各省市的工业环境效率进行静态评价。实证结果表明：2005—2014年长江经济带整体工业环境效率水平较高，但各地区之间仍然存在一定差距，其中浙江、江苏等地环境效率值较高，云南、贵州等地较低；11个省市的全要素环境效率的增长率平均值大于1，技术进步是工业环境效率变动的主要因素；产业结构和环境管制对工业环境效率产生积极影响，外商投资和人口密度对工业环境效率产生消极影响。

长江经济带；工业环境效率；超效率DEA；Malmquist指数；Tobit回归模型

一、引 言

长江经济带横贯中国东中西3大域，覆盖上海、江苏、浙江、安徽、江西、湖北等11个省市。2014年3月，李克强总理在《政府工作报告》中明确提出“依托黄金水道，建设长江经济带”。然而，在长江经济带经济增速持续高于全国平均水平的同时，环境污染问题与工业化相伴而生，资源承载力也受到了挑战，其发展经历了一个“低水平均衡→非均衡→高水平均衡”的“倒U型”动态演进过程[1]。丁黄艳等运用能源强度、离散系数、莫兰指数综合测度1999—2013年长江经济带工业能源效率空间差异，结果表明长江经济带省际工业能源效率存在梯度差异，呈空间集聚特征[2]。从某种程度上来说，转变经济发展方式首先就是转变粗放型经济增长模式[3]。我国目前正处于工业化和城市化加速推进的状态，工业是国民经济的支柱产业，而工业生产又是导致资源与环境恶化的主要来源，因此研究长江经济带11个省市的工业环境效率差异及其影响因素对提高工业资源利用率、实现经济可持续发展具有重要理论及现实意义。

工业环境效率是指工业系统创造单位价值产生的环境影响的大小[4]，从研究角度来看，工业环境效率的研究更多地从当初的企业层面逐步向更加微观和宏观两个层面深入，且趋于重污染企业或行业发展[5]，主要集中在区域[6]方面，包括城市[7]、省域[8]及国家层面[9]，而对经济带的研究却不多。从研究内容来看，很多学者都通过非参数的数据包络分析方法对工业环境效率进行测度研究，例如，Charnes等首次提出基于规模报酬不变的DEA模型对效率进行研究，此方法无需设定生产函数的具体形式，评价结果较为客观[10]。若利用DEA模型进行工业环境效率的评价，是需要将环境因素引入模型中，而环境因素中并不只包含期望产出，环境的污染排放通常被人们称为非期望产出，Fare等为了解决这一问题，首次提出了包含非期望产出的DEA模型[11]。除Fare之外，Chung等也通过利用不断发展的数据包络分析方法来研究工业环境效率领域[12-13]。传统的DEA模型在多个决策单元同时有效的情形下是无法做出进一步的评价的，所以Anderson等建立了超效率DEA模型[14]，在此基础上Xue等推广了该模型[15]。近年来，庞瑞芝等[3，16-17]都采用超效率DEA模型对效率问题进行研究。与此同时，也有很多文献集中研究环境效率影响因素的定性问题，如白永平等认为中国市场化程度的提高对环境效率的提高也有一定的正向作用[18]。

然而，已有文献仍然存在以下不足之处：第一，国内外大多文献多以省域或国家为研究单位，缺乏对“经济带”的研究，笔者将以长江经济带为研究对象来弥补这方面的不足；第二，已有文献大多从静态或者动态单一角度对工业环境效率进行研究[19]，笔者同时从这两个角度进行研究；第三，已有文献大多是采用截面数据对影响因素进行分析，笔者将采用Tobit面板数据模型来分析各因素对工业环境效率变化的影响。

二、研究方法及数据说明

1.研究方法

在现有文献中，DEA方法计算出来的相对效率有很多优点，如针对前沿生产函数不必确定其具体形式、在研究多投入多产出问题时弥补权重给定的主观性、减少计算误差等。鉴于以上优点，笔者也利用DEA方法对长江经济带工业环境效率进行研究。

(1)超效率DEA模型

当前，数据包络分析是研究环境能源效率的主流方法，特别是超效率DEA模型[14]。相比传统DEA模型而言，其把所评价的决策单元排除在生产可能集外，使相对有效的决策单元也能够进行效率评价，因而超效率DEA在效率评价领域得到了广泛的应用。

假定有n个独立DMU，每一个DMU中都有m种投入xj和s种产出yj，则超效率DEA模型的具体形式如下[20]：

(1)

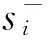
(2) Malmquist指数模型

Malmquist生产率指数首先是由Sten Malmqusit在1953年分析不同时期的消费变化时提出的，后由Caves等利用该指数模型进行生产率变化的测算[21]，才形成如今的Malmqusit生产率指数模型。Malmqusit指数模型是以距离函数为基础的，核心思想就是将此转化为基于效率函数定义的Malmqusit指数模型。根据Fare等人的研究，将指数进行分解为技术变化和技术效率变化[22]，则Malmqusit生产指数(TFPch)的计算公式如下：

(3)Tobit面板回归分析

对工业环境效率的影响因素的分析将通过两阶段分析法[23]，首先通过DEA模型评估出决策单位的工业环境效率值，并将此定义为因变量，除此之外，工业环境效率还受投入产出变量之外其他因素的影响，因此将其他影响因素定义为自变量，然后建立计量经济模型来分析。相对环境效率指数在一定的数值域内，Greene指出，对于这种存在数据截断的受限因变量模型，如果用普通最小二乘法进行回归系数分析，参数估计值会出现偏差[24]，因此Tobit模型提出采用极大似然法的截取回归模型。具体形式为

(3)

式中：i为不同的决策单元；Yi即为第i个决策单元的相对环境效率值；Xi为自变量；βt是未知参数变量，ui～N(0,σ2)，i=1,2,3,…。

2.指标及数据说明

在实际运用中，投入指标通常选择资本、劳动等传统投入，并将收益性指标用作产出指标，但笔者研究工业环境效率需要增加环境污染指标，因此借鉴已有文献研究成果[18]将环境污染排放量作为非期望产出指标，同时兼顾数据的完整性、科学性与可得性，选取长江经济带11个省市2005—2014年的数据为决策单元构建长江经济带工业环境效率的指标体系(表1)。

表1 工业环境效率评价指标

具体的投入产出指标构成如下：

①资本投入。将工业资本存量作为资本投入要素，借鉴岳书敬的计算方法[25]得出各地区历年的工业资本存量，为消除价格影响，通过每年利用固定资产投资价格指数折算成2005年不变价，单位为亿元，公式为

(4)

式中：Ki,t0表示i地区2005年的固定资产净值，Δki,t表示i地区t年的名义净投资，其中固定资产净值由固定资产原价合计与累计折旧的差得到，Pt表示t年的固定资产投资的价格指数值。

②劳动投入。由工业企业全部从业人员年平均人数得到，由于研究的是工业部门的数据，可以不考虑从业人员素质和劳动时间差异的影响，单位为人。

③环境污染产出。为准确反映污染物的排放水平，选取工业废水排放量、工业COD排放量和工业二氧化硫排放量作为非期望产出指标。DEA模型要求产出越大越好，因此需要对非期望产出进行转换。处理非期望产出的常用方法有：一是将非期望产出作为投入变量进行处理，但这种方法与物质平衡法相互违背；二是采用线性数据函数转换方法，这是一种较好的环境效率评价方法。因此采用第二种方法进行分析，原理是线性数据转化函数[26]，即将环境污染排放转化为期望产出，具体公式为：

f(χit)=max(χt)+1-χit

(5)

式中：χit为第t年第i个省份的污染物排放原值，max(χt)+1为第t年污染物排放的最大值，来保证所有转化的期望产出为正数。

④工业产出。由工业增加值获得，为了消除价格因素的影响，以2005年为基期，利用各年份工业品出厂价格指数折算成2005年不变价。

投入产出指标数据来源于《中国统计年鉴》《中国城市统计年鉴》《中国环境统计年鉴》以及各省份《环境统计公报》。

三、实证分析

1.工业环境效率静态分析

基于产出导向规模报酬不变超效率DEA模型，根据EMS1.3软件对长江经济带11个省市2005—2014年的工业环境效率值进行测算(表2)。

结果表明：①从横截面数据分析，2005—2014年，长江经济带工业环境效率的平均值均达到了较高的效率前沿。这种较高的平均值结果直接得益于我国“十一五”规划的实施，这一时期长江经济带在发展工业的同时兼顾生态环境的保护，在较高程度上实现了工业发展与资源环境的协调发展。②从时间序列数据分析，长江经济带11个省市在2005—2014年，差异性比较明显。总体来看，可以将11个省份划分为3类地区：环境效率值相对较高的省份(浙江、江苏、四川、安徽，平均值均达到或超过1.20)、环境效率值处于中等的省份(湖北、湖南、江西和上海等省份，平均值介于1～1.2之间)、环境效率值相对较低的省份(贵州、重庆、云南，平均值均小于1)。

表2 2005—2014年长江经济带11省市工业环境超效率值

第一类是超效率平均值较高的地区，在这类地区中，既有处于长江经济带中下游的经济发达地区，也有处于经济带中上游的经济欠发达地区。前者很大程度上归因于长江下游地区是我国对外开放的前沿城市、更容易引进国外先进理念与技术，在发展工业的同时减少资源的消耗与排放，工业发展与资源环境的利用达到了高效的协调；后者更多是因为经济与环境协调发展使其呈现出较高的环境效率，说明环境效率的提高并不是盲目追求GDP总量的增加，各省既要追求经济发展，也要注重环境保护。第二类是超效率平均值处于中等的湖南、湖北、江西和上海等地区。其中，除上海外，其他省份都处于长江经济带中游地区，虽然区域竞争中的劣势以及发达城市的污染转移使其超效率值低于江苏等地，但通过与周边经济发达省份的区域合作以及“十二五”规划开局的实施，对工业发展与资源环境的协调发展起到了一定的促进作用，使其呈现出不低的超效率值。上海是我国经济最发达的城市，同时也是资源稀缺的大型地区，经济的快速增长与人口压力使城市运行成本增加，经济快速增长的正效益受到环境问题带来的负效益影响，使其超效率值处于经济带中等阶段。第三类是超效率平均值较低的地区。贵州、重庆和云南这类效率值相对较低的省份都属于长江经济带上游地区，经济基础薄弱且生产技术落后，经济发展依赖于“高污染、高消耗”的传统制造业，工业经济增长的同时需要消耗较大的资源，因此呈现出较低的工业环境效率值。

2.工业环境效率动态分析

根据2005—2014年长江经济带11个省市的数据，利用DEAP2.1软件，得到11个省市总体分年份和分地区的全要素工业环境效率变动指数(表3～4)。

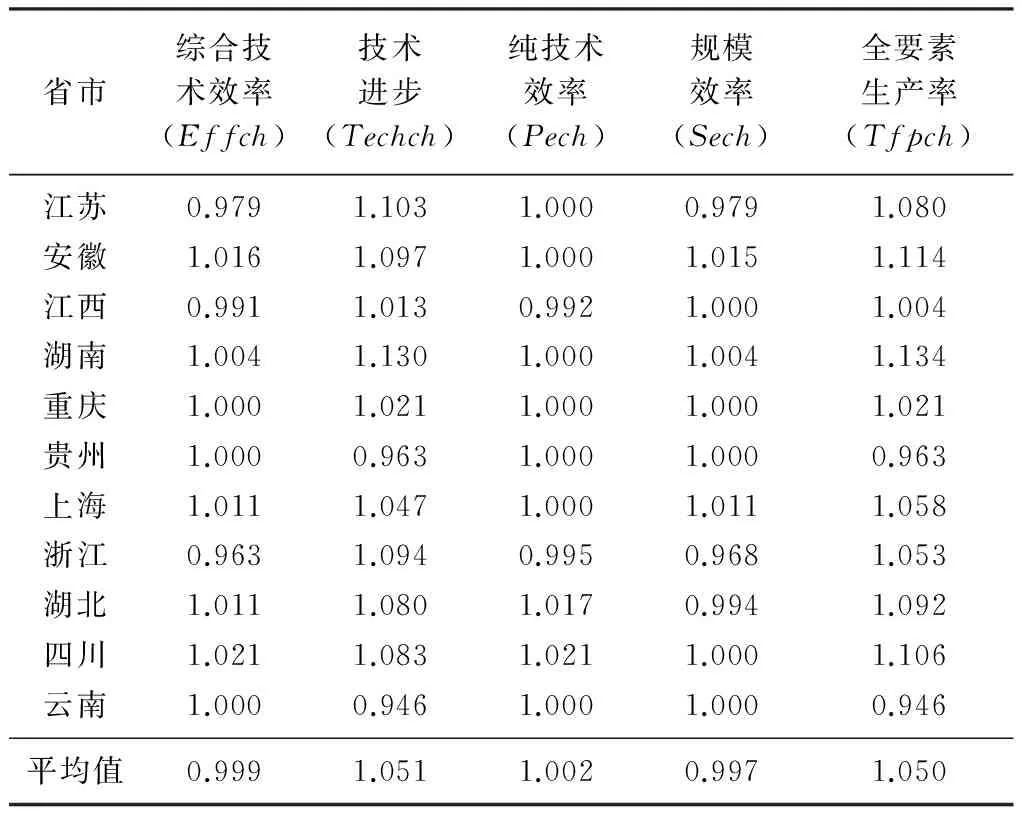
表3 2005—2014年长江经济带11个省市年平均Malmquist指数及其分解

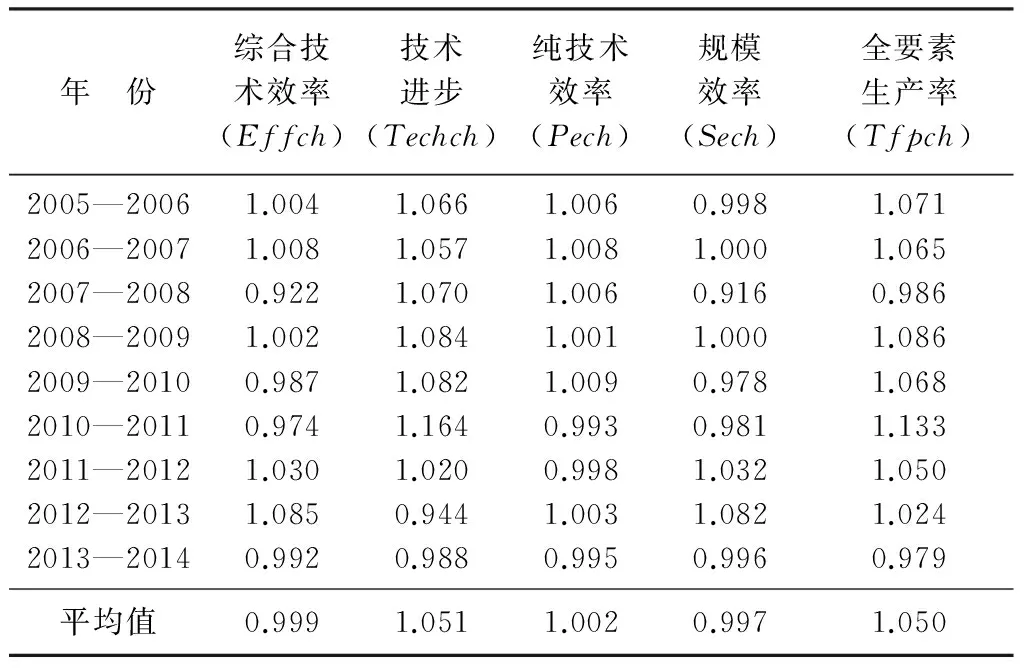
表4 11个省市各年份平均Malmquist指数及其分解

从表3可以看出，长江经济带2005—2014年11省市的全要素工业环境效率的平均变动指数为1.050，年均增长率为5%。从年均增长率的分解来看，技术进步(Techch)和纯技术效率(Pech)增长率是增加的且技术进步的增长率高于纯技术效率的增长率，而综合技术效率和纯技术效率是下降的，可知各省市工业环境效率的增长率最大程度上是得益于技术进步的增长。以重庆为例，其综合技术效率、纯技术效率和规模效率均不变，只有技术进步增长2.1%，可以发现TFP的增加是来源于技术进步的增长；另外，贵州和云南环境效率处于下降的趋势，贵州年均下降3.7%，云南年均下降5.4%，均归因于技术进步的下降。由表2可知，两地目前都处于环境效率值较低的地区，仍一直处于下降的趋势，与表2研究结果一致。因此可知云南、贵州等地特殊的经济结构并不适合我国，需要引进先进技术，加强对新技术的吸收与应用，调整产业结构，促进产业结构的优化升级。

从表4可知，虽然最近两年有所下降，但长江经济带工业环境效率整体上呈现逐年提高的态势，技术进步是长江经济带11个省市工业环境效率增长的主导因素，平均值最高已经达到了5.1%。

四、工业环境效率影响因素分析

影响工业环境效率的因素有很多，在参考以往研究文献成果[17,27-28]的基础上，从3个层面考虑影响因素：①经济层面：一是经济发展水平X1，属于经济层面的总量指标，用人均GDP的对数来表示(LNGP)；二是产业结构X2，属于经济层面的质量指标，用工业增加值与地区GDP的比重来表示(PT)。②制度层面：一是外商投资X3，选取地区实际利用外资额与地区生产总值的比重(WZ)；二是环境管制X4，取排污费收入的对数(LNFI)。③地域层面X5：选取各省市人口密度的对数(LNPD)作为研究指标。

借助Eviews6.0软件，通过极大似然估计法对Tobit模型数据进行处理并进行回归(表5)。

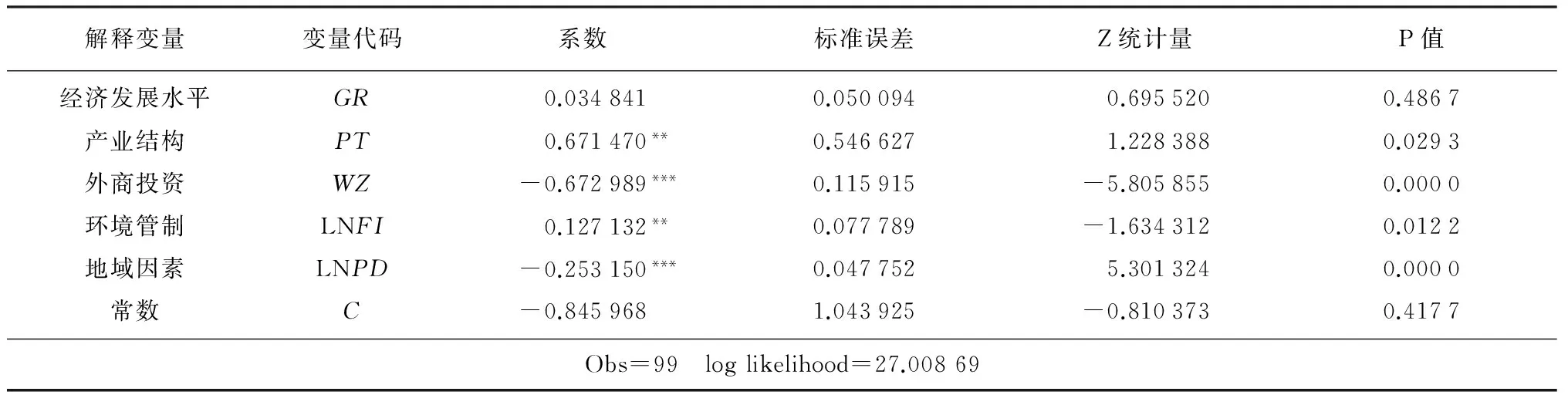
表5 Tobit回归结果

注：***，**分别表示通过了1%，5%的显著性检验。

第一，从经济层面来看，经济发展规模与工业环境效率的关系比较模糊。Tobit回归结果表明，经济发展水平对各省市的影响系数为0.034 841，但P值为0.486 7，在10%的显著性水平上未通过检验，而象征质量指标的产业结构系数却为正，且通过了5%的显著性水平检验。也就是说，长江经济带各省份经济发展水平与工业环境效率值没有直接的影响关系，如经济发达的江苏、浙江与经济欠发达的四川、安徽环境效率值都处于前列，产业结构的调整能够使工业环境效率得到改善。因此，通过提高技术创新能力、培植新兴产业、调整产业结构及促进产业结构的优化升级更能对工业环境效率产生积极的影响。

第二，从制度层面来看，首先外商投资(WZ)与工业环境效率负相关。Tobit结果表明，外商投资对各省市的影响系数为负，且在1%的显著性水平上通过了检验，这种情况与实际情况相符。外商对各省市的投资很大程度上集中在钢铁等工业领域，而各省份更多关注经济发展规模未能有效控制其投资方向，自然会使工业环境效率受到负面影响；制度层面的环境管制与工业环境效率正相关，环境管制(LNFI)系数为正，并且在5%的显著性水平下通过检验，这表明环境管制是影响工业环境效率的有效指标，分析其原因可知，近十几年来国家环境管制力度的加强，促使各省份采用清洁技术生产和末端治理，在发展经济的同时注重环境的保护，促进经济的可持续发展。

第三，从地域层面来看，人口密度与工业环境效率负相关。回归结果表明，人口密度对环境效率的影响系数为负，且P值为0表明各省份在指标上存在显著差异，也就是说，人口密度的增大会对工业环境效率产生破坏。原始数据可以印证这一观点，人口密集的重庆、上海等地环境污染排放相对较严重，因此需要正视人口增长对经济与环境的威胁，促进长江经济带地区人口、资源与环境的协调发展。

五、结论与启示

基于长江经济带11个省市的面板数据，利用超效率DEA模型和Malmquist指数对11个省市的工业环境效率进行测算和分解，在此基础上，采用Tobit模型对工业环境效率的其他影响因素进行分析，结论如下。

第一，工业环境效率的超效率DEA结果显示，长江经济带11个省市2005—2014年的超效率均值从横截面数据来看工业环境效率均达到较高的效率前沿面，而从时间序列数据来看，各省份之间环境效率值仍有一定的差距。其中，浙江、江苏等地效率值较高，云南、贵州等地较低。因此，为解决各地区之间的差异，从整体上提高工业环境效率，政府首先需要采取措施对这些地区进行技术引进以及财力上的支持；其次，各地区各企业需要调整产业结构，对传统产业实行节能减排的措施，围绕重点产业进行产业链整合，注重环境与经济之间的平衡，提高环境利用效率，发展循环经济；最后，要综合考虑各省份间的发展政策之间的冲突，加强引导各省份进行区域合作交流，培养各省份的自主创新能力，加快推动各省份之间和谐的环境合作机制，最终实现工业环境效率的提高。

第二，通过对11个省市平均Malmquist指数的分解可以看出技术进步对长江经济带工业环境效率的变动起主导作用。因此，为提高长江经济带地区工业环境效率的增长率，可以从3方面进行考虑：首先要促进11个省市之间的技术交流与合作，合理引用先进技术与理念，注意新技术的吸收应用，避免引进“高污染、高消耗”的产业，造成工业环境压力过大；其次，使各省份资源得到合理配置，以重点产业为核心对产业结构进行优化升级，使规模效率得到提高；最后，要加大科技投资力度，鼓励各大中型企业对科研投入的积极性，促使科研经费来源渠道的拓宽，促进科学技术转化为生产力。

第三，通过Tobit模型分析影响工业环境效率的外在影响因素，结果表明产业结构和环境管制对工业环境效率产生显著的正相关，外商投资和人口密度对工业环境效率产业了显著的负相关。从外在影响因素入手提高工业环境效率，首先需要调整产业结构，一方面积极引领企业走新型工业化道路，另一方面努力挖掘各省市的优势产业并加强引导各省市进行有效的区域合作；其次，加强环境管制，促进各省份在提高经济发展的同时注意环境的保护，采取加强排污费收入等各项有效措施；另外，需要在合理引进外资、引进国外先进技术和设备的同时注重调控外商投资的方向，引领外商向低污染产业发展，使外资合理利用在循环经济领域；最后，减少人地矛盾，合理分布各地区人口，促进人口、资源与环境的协调发展，提高工业环境效率。

[1] 成长春.长江经济带协调性均衡发展的战略构想[J].南通大学学报(社会科学版)，2015，31(1)：1-8.

[2] 丁黄艳，任毅，蒲坤明.长江经济带工业能源效率空间差异及影响因素研究[J].西部论坛，2016，26(1)：27-34.

[3] 庞瑞芝，李鹏.中国新型工业化增长绩效的区域差异及动态演进[J].经济研究，2011(11)：36-48.

[4] VERFAILLIE H A,BIDWELL R.Measuring eco-efficiency：a guide to reporting company performance [M].Geneva：World Business Council for Sustainable Development,2001.

[5] 王飞儿，史铁锤.基于物质代谢的中国纺织业生态效率评价[J].中国人口·资源与环境,2008,18(16)：116-120.

[6] SEPPALAA J,MELANEN M,MAENPAA I,et al.How can the eco-efficiency of a region be measured and monitored [J].Journal of Industrial Ecology,2005,9(4)：117-130.

[7] 袁鹏，程施.中国工业环境效率的库兹涅茨曲线检验[J].中国工业经济,2011(2)：79-88.

[8] 吴小庆，王远，刘宁同，等.基于物质流分析的江苏省区域生态效率评价[J].长江流域资源与环境,2009,18(10)：890-895.

[9] 杨斌.2000—2006年中国区域生态效率研究：基于DEA方法的实证分析[J].经济地理,2009,29(7)：1197-1202.

[10] CHARNES A,COOPER W W,RHODES E.Measuring the efficiency of decision making units[J].European Journal of Operational Research,1978,2(6)：429-444.

[11] FARE R,GROSSKOPF S.Multilateral productivity comparisons when some outputs are undesirable:a nonparametric approach[J].The Review of Economics and Statistis,1989,71(1)：90-98.

[12] CHUNG Y,FARE R,GROSSKOPF S.Productivity and undesirable outputs：a directional distance function approach[J].Journal of Environmental Management,1997,51(3)：229-240.

[13] TONE K.A slacks-based measure of efficiency in data envelopment analysis[J].European Journal of Operational Research,2001,130(3)：498-509.

[14] ANDERSEN P,PETERSEN N C.A procedure for ranking efficient units in data envelopment analysis[J].Management Science,1993,39(10)：1261-1264.

[15] XUE M,HARKER P T.Note：ranking DMUs with infeasible super-efficiency DEA models[J].Management Science,2002,48(5)：705-710.

[16] POVEDA A C.Economic development and growth in Colombia：an empirical analysis with super-efficiency DEA and panel data[J].Socio-Economic Planning Sciences,2011,45(4)：154-164.

[17] 胡根华,秦嗣毅.“金砖国家”全要素能源效率的比较研究：基于DEA-Tobit模型[J].资源科学,2012,34(3)：533-540.

[18] 白永平,张晓州,郝永佩,等.基于SBM-Malmquist-Tobit模型的沿黄九省(区)环境效率差异及影响因素分析[J].地域研究与开发,2013,32(2)：90-95.

[19] 焦兵,孙君厚.丝绸之路经济带工业环境效率的动态评价及影响因素研究[J].统计与信息论坛,2015,30(11)：44-48.

[20] 孟晓,孔群喜,汪丽娟.新型工业化视角下“双三角”都市圈的工业能源效率差异：基于超效率DEA方法的实证研究[J].资源科学,2013,35(6)：1202-1210.

[21] CAVES D W,CHRISTENSEN L R,DIEWERT W E.The economic theory of index numbers and the measurement of input,output and productivity[J].Econometrica,1982,50(6)：1393-1414.

[22] FARE R,GROSSKOPF S,NORRIS M.Productivity growth,technical progress,and efficiency change in industrialized countries[J].American Economic Review,1994,84(1)：66-83.

[23] COELLI T J,RAO D S P,O’DONNELL C J,et al.An introduction to efficiency and productivity analysis[M].Boston：Kluwer Academic Publishers,1998.

[24] GREENE W H.On the asymptotic bias of the ordinary least squares estimator of the Tobit model[J].Econometrica,1981,49 (2)：505-513.

[25] 岳书敬.基于低碳经济视角的资本配置效率研究：来自中国工业的分析与检验[J].数量经济技术经济研究,2011(4)：110-124.

[26] SEIFORD L M,ZHU J.Modeling undesirable factors in efficiency evaluation[J].European Journal of Operational Research,2005,161(2)：579-581.

[27] 李青松,徐国劲,邓素君,等.基于DEA-Malmquist-Tobit模型的河南省生态效率研究[J].环境科学与技术,2016,39(4)：194-199.

[28] 汪克亮,孟祥瑞,杨宝臣,等.基于环境压力的长江经济带工业生态效率研究[J].资源科学,2015,37(7)：1491-1501.

(责任编辑：高 虹)

10.3876/j.issn.1671-4970.2017.03.009

2016-11-28

江苏省社会科学基金项目(12EYB008)；江苏省博士后基金(1202087C)；河海大学中央高校基本科研业务费项目(2015B10114)

马骏(1970—)，男，江苏金湖人，博士，副教授，从事技术经济及循环经济研究。

F061.5；F403

A

1671-4970(2017)03-0049-06