混凝土梁中GFRP筋抗拉强度可靠性随半径和扩散系数的变化规律
2017-07-05杨俊峰韩丽丽河南省交通规划设计研究院股份有限公司郑州450000河南省交通科学技术研究院有限公司郑州450000
杨俊峰韩丽丽(.河南省交通规划设计研究院股份有限公司,郑州450000; .河南省交通科学技术研究院有限公司,郑州450000)
混凝土梁中GFRP筋抗拉强度可靠性随半径和扩散系数的变化规律
杨俊峰1韩丽丽2
(1.河南省交通规划设计研究院股份有限公司,郑州450000; 2.河南省交通科学技术研究院有限公司,郑州450000)
混凝土梁中G FR P筋抗拉强度值受混凝土聚合物扩散系数、碱性物质浓度、G FR P半径、作用时间等因素的影响,考虑变量因素的不确定性,引入统计独立零均值、单位方差的随机变量,建立了G FR P筋抗拉强度的半概率可靠性预测模型预测G FR P筋抗拉强度。根据试验数据和预测结果对比,半概率可靠性预测模型预测的绝对误差为2.89M P a,相对误差为0.54%,相对于G M(1,1)预测模型和线性拟合方法的精度更高。运用正交变换法计算不同半径和扩散系数的G FR P筋强度可靠性指数,得到相应的结构功能函数和功能函数梯度,通过计算得到混凝土梁中G FR P筋可靠性指数与扩散系数、G FR P筋半径的关系。
桥梁工程半概率可靠性模型正交变换可靠性指数G FR P筋
0 引言
钢筋混凝土结构是建筑结构的主体,其耐久性的研究一直受到世界广泛关注,以上世纪七十年代基础设施就相对完善的美国来讲,目前在所有的结构破坏中,钢筋锈蚀破坏占55%。特别是以桥梁为代表的钢筋混凝土基础设施的锈蚀破坏已成为当今世界突出的问题。钢筋的锈蚀是使结构功能退化的主要原因之一,针对这一现状,国内外兴起使用纤维聚合物材料FRP筋,尤其是性价比优越的GFRP筋作为混凝土中钢筋代替品或者部分代替品,然而这样一种广泛应用的趋势是受到GFRP筋混凝土耐久性理论研究的滞后所限制。因而研究GFRP筋在混凝土中的性能将是广泛推广其应用的必要条件。
GFRP筋替代钢筋作为结构的受力筋,其寿命期抗拉强度的行为是GFRP筋混凝土技术发展的基础研究。在实际工程中,GFRP筋会受到各种环境及人为因素的影响,不断对其性能产负面效应。现有的预测模型主要是基于菲克定律(Fick’s Law)的预测模型[1]和基于阿列纽斯定律(Arrhenius equation)的预测模型[2]。基于菲克定律(Fick’s Law)的预测模型假定当渗透发生到一定程度,玻璃纤维完全暴漏在扩散的溶液中,此时纤维进入完全失效状态,退出GFRP筋工作。Tannous和Saadatmanesh分析了GFRP材料吸水量和抗拉强度的关系来预测GFRP筋残留强度。Trejoetal提出考虑玻璃纤维和基质粘结强度老化的依时性。阿列纽斯(Arrhenius)方程的预测模型主要是建立起材料在加速老化实验中所得到数据与实际使用年限的关系。
GFRP复合材料的长期耐久性试验数据不足,在以往的研究过程中大多做出了相应的假设,但是这些假设未能完全考虑到GFRP筋使用过程中可能存在统计参数的不确定性,模型误差等因素,因此,以往模型的系统误差较为明显。本文针对混凝土中GFRP筋强度建立相应的半概率可靠性模型,并且应用正交变化法计算其在不同年限的失效概率和可靠性,这对于研究GFRP筋的长期耐久性行为具有指导意义。
1 混凝土梁中GFRP筋抗拉强度半可靠性概率理论预测模型
混凝土梁中GFRP筋耐久性长期行为研究依赖于长短期行为资料的积累。由于国内外缺乏长期行为数据,所以目前仍根据短期加速试验数据来研究GFRP筋耐久性长期行为,促进GFRP筋混凝土设计理论的发展。如前所述:尽管近年来美国混凝土协会(ACI)颁布了试验方法指南,美国标准试验协会(ASTM)颁布了标准试验方法[3-4],但目前大部分研究工作的前提条件,如所采用的GFRP筋的材料种类及组成、试验方法等,皆不完全相同,导致其实验结果无法按定量的方法进行比较分析[5]。而且目前所采用的按Fick定律和Arrhenius方程进行长期性能的预测需满足特定的条件,有严格的限制。因此需要研究一个多参数随机变化的半可靠性的概率型预测模型来解决上述问题[6]。
上面受持续荷载、带工作裂纹GFRP筋混凝土梁中GFRP筋抗拉强度加速试验短期行为研究,GFRP筋聚合物玻璃软化温度与GFRP筋聚合物的碱性物质扩散两个机理的研究,完善了受持续荷载、带裂纹工作的GFRP筋混凝土梁中GFRP筋抗拉强度的研究数据,与目前国内外有关成果一起为多参数随机变化的半概率可靠性理论研究提供了条件[7]:
Katsuki和Uomoto提出如下的长期抗拉强度预测模型[8]:
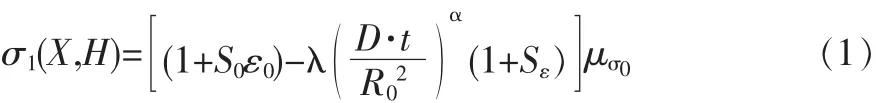
式中,σ0、σt分别为暴露于环境作用之前和之后的抗拉强度(非实际应力);D为聚合物扩散系数,C为碱性物质浓度(百分数),t为作用时间,R0为GFRP筋半径。令X=(R0,D),为基本向量(即t=0时GFRP筋半径和聚合物扩散系数);ε0、ε分别为统计独立零均值、单位方差的随机变量;S0、S分别为ε0、ε的标准差;S0ε0是均值为μσ0的变量σ的误差项;Sε是退化项λ)α的误差项;H=
0
(λ,α,S0,S)为适应实验数据的未知经验模型参数向量。上述模型有两个假定(可证明其有效性):S0、S与X独立;ε0、ε具有正态分布。
2 半概率可靠性理论预测模型精度分析
预测混凝土梁中GFRP筋抗拉强度,需要确定各个参数的具体取值,由David Trejo.paolo Gardoni,Jeong Joo Kim.and Jason Zidek所做的GFRP筋长期行为试验数据得到GFRP筋的强度为μσ0=610.23MPa,其余试验数据如下表1所示,根据ACI 440规范[9]未暴露于外界环境的混凝土中GFRP筋的设计强度σACI440=0.8μσ0=488.1840MPa,扩散系数D=0.0000000000007m2/s,材料半径R0=0.016m。
根据上述试验数据和变量的概率分布,根据贝叶斯理论,经过运算得到参数向量H(λ,α,S0,S)的估计值[10]如下表2:
那么根据式(1)模型描述以及表2的参数估计值,用半概率可靠性理论预测模型预测得到的该环境下(PH= 12,温度T=70°F)混凝土梁中GFRP筋7年(350周)的抗拉强度为534.32MPa,而David Trejo.paolo Gardoni,Jeong Joo Kim.and Jason Zidek所做的GFRP筋长期行为试验数据显示7年(350周)的GFRP筋抗拉强度为537.21MPa,预测绝对误差为2.89MPa,相对误差为0.54%。
传统依据少量数据进行预测的方法有灰色预测方法和线性拟合法,因此,建立相应的GM(1,1)模型和线性回归模型与半概率可靠性模型进行精度对比可以找出精度最高的一种预测方法。
GM(1,1)模型要求原始数据个数必须大于5个[11],因此,以0周~150周的GFRP筋抗拉强度试验值为原始数据,预测其7年(350周)的抗拉强度值符合GM(1,1)模型的要求。通过对试验数据的处理和计算,得到模型σt=-0.00312t+571.675,GM(1,1)模型的后验差检验值为0.0811,根据后验差检验判别表,后验差检验数小于0.35,GM(1,1)模型的评价为优[12],所以,GFRP筋抗拉强度GM(1,1)预测模型判定为优,其预测结果较为可靠。GFRP筋7年(350周)灰色预测值为511.65MPa,而对应时间的试验值为537.21MPa,半概率可靠性模型预测值为528.08MPa,此时GM(1,1)模型的预测绝对误差为25.56MPa,相对误差为4.76%,而半概率可靠性模型的绝对误差为2.89MPa,相对误差为0.54%,明显看出,半概率可靠性预测模型的预测精度明显高于GM(1,1)预测模型。

表1 已知试验数据

表2 H(λ,α,S0,S)后验分布统计参数
3 不同半径和扩散系数混凝土梁中GFRP筋强度可靠性分析
上文得到了混凝土梁中GFRP筋抗拉强度的半概率可靠性预测模型,结合模型应用结构可靠度计算中的正交变换发[13]得到结构功能函数和功能函数梯度如下:
结构功能函数:

根据正交变换法的算法编写相应的MATLAB程序,在环境(PH=12,温度T=70°F)下混凝土梁中GFRP筋(扩散系数D=0.0000000000007m2/s,材料半径R0=0.016m)7年(350周)的强度失效概率为0,而此时GFRP筋的抗拉强度为537.21MPa,相对于ACI 440规范未暴露于外界环境的混凝土中GFRP筋的设计强度σACI440=0.8μσ0= 488.1840MPa而言,此时GFRP筋抗拉强度未失效,这与实际情况是相吻合的。
考虑扩散系数,根据Trejo等学者的研究,扩散系数的取值范围大约在D=0.000000000000288m2/s~0.000000000000154m2/s、材料半径R0=0.01m~0.02m混凝土梁中GFRP筋第7年的可靠性指数,计算结果如下图1所示:

图1 GFRP筋第7年可靠性指数
由图1可以看出,当混凝土扩散系数0.000000000000288m2/s≤D≤0.0000000000006m2/s时,梁中GFRP筋的抗拉强度可靠性指数随着GFRP筋的半径增加而减小;当混凝土扩散系数D≥0.0000000000006m2/ s时,梁中GFRP筋的抗拉强度可靠性指数随着GFRP筋的半径增加先增加后减小;GFRP抗拉强度可靠性指数在半径0.011m~0.015m、扩散系数0.0000000000008m2/s≤D≤0.00000000000014m2/s的带状区域内达到最大值,即此时GFRP筋抗拉强度失效概率最低。
计算100年内扩散系数D=0.0000000000007m2/s,材料半径R0=0.016m混凝土梁中GFRP筋的失效概率(可靠性指数),作为其长期性能预测的结果进行研究参考和分析。
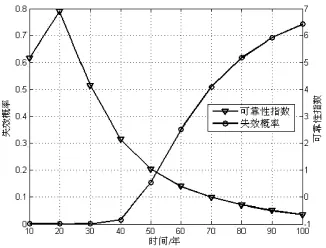
图2 GFRP筋抗拉强度可靠性(失效概率)100年变化规律
图2 为100年内混凝土梁中GFRP筋的可靠性和失效概率的变化,可以明显看出,在一定的环境条件下,前期GFRP筋的抗拉强度比较稳定,也就是说GRRP筋在这段时间内强度几乎不损失。到了一定时间后,混凝土中GFRP筋的抗拉强度急剧损失,反应在可靠性指数和失效概率上就是可靠性指数明显降低失效概率显著增加,这样的结果可以说明在这段时间内,混凝土梁中GFRP筋的抗拉强度发生了较大的变化,造成强度急剧下降的原因可能是以下的原因:GFRP筋由玻璃纤维和聚合物基体组成。当GFRP筋用在混凝土内部,并作为受力筋时,由于潮湿或碱性溶液等的存在导致玻璃纤维被侵蚀。GFRP筋梁处于潮湿和碱性环境中,水分和碱性溶液会扩散进入聚合物基体,甚至到达玻璃纤维,侵蚀这些纤维。正是由于前期的荷载作用造成了聚合物集体有所开裂,这样水分和其他侵蚀容易就以更加快的扩散速率达到玻璃纤维。
4 结语
(1)GFRP的半径和混凝土的扩散系数对于混凝土梁中GFRP筋的抗拉强度值或者抗拉强度可靠性(失效概率)有很显著影响。
(2)混凝土梁中GFRP筋抗拉强度的半概率可靠性预测模型预测精度远高于GM(1,1)预测模型和线性拟合预测方法。
(3)混凝土扩散系数偏大时,混凝土梁中GFRP筋抗拉强度的可靠性随GFRP筋半径增加先增加后降低,抗拉强度失效概率随GFRP筋半径增加先降低后增加;混凝土扩散系数偏小时,GFRP筋半径越大,混凝土梁中GFRP筋抗拉强度的可靠性越低,抗拉强度失效概率越大。
(4)混凝土梁中GFRP筋抗拉强度在某个时间点的最小失效概率(或者最大可靠性指数)并非半径最大和混凝土扩散系数的组合,由于两者的共同影响,极值点应在某一带状区域内找出。
(5)混凝土梁中GFRP筋抗拉强度在使用初期强度值损失较大,损失速率较快,到后期强度损失速率逐渐减慢。
[1]Shen,C.H.,and Springer,G.S.Moisture Absorption and Desorption of Composite Materials[J].Journal of Composite Materials,1976,10(1)∶2-20.
[2]Litherland,K.L.,Okley,D.R,and Proctor,B.A.The use of accelerated aging procedures to predict the long term strength of GRC composites[J].Cem.Concr.1981,11(3)∶455-456.
[3]ASTM Committee D20,D 3916–08.Standard Test Method for Tensile Properties of Pultruded Glass-Fiber-Reinforced Plastic Rod [Z],2008.
[4]ASTM Committee D30,D 7205/D 7205M–06.Standard Test Method for Tensile Properties of Fiber Reinforced Polymer Matrix Composite Bars[Z],2006.
[5]HE Xiong-jun,YANG Jing-nan,Charles E.Bakis.Tensile strength characteristics of GFRP bars in concrete beams with work crack under sustained loading and severe environments.Journal ofWuhan University of Technology(materials science edition),2013(5)∶15-18.
[6]Mias,C,Torres,Li,Turon,A Effect ofmaterials properties on longterm deflections of GFRP reinforced concrete beams[J].Construction and Building Materials,2013,41∶99–108.
[7]Kim,B,Doh,J.-H,Yi,C.-K.Effects of structural fibers on bonding mechanism changes in interface between GFRP bar and concrete. Composites Part B-Engineering[J],2013,45∶768–779.
[8]David Trejo.paolo Gardoni,Jeong Joo Kim.and Jason Zidek.Longterm Performance of GFRP Reinforcement[R].Texas∶Texas Transportation Institute,the Texas A&M University System College Station,2009∶53-54.
[9]American Concrete Inst.,Farmington Hills.ACI 440.1R-06,Guide for the design and construction of concrete reinforced with FRP bars [Z],2006
[10]David Trejo.paolo Gardoni,Jeong Joo Kim.and Jason Zidek.Longterm Performance of GFRP Reinforcement[R].Texas∶Texas Transportation Institute,the Texas A&M University System College Station,2009∶56-57.
[11]李福琴,刘建国.数据变换提高灰色预测模型精度的研究[J].统计与决策,2008(6)∶15-17.
[12]郭云开,陈刚,谢腾,乐小勇.路基深层水平位移预测方法[J].长沙理工大学学报:自然科学版,2012(9)∶19-24.
[13]洪昌华,龚晓南.相关情况下Hasofer-Lind可靠度指标的求解[J].岩土力学,2000,21(1)∶68-71.
